一种利用测井渗透率进行地层有效裂缝的识别方法与流程

本发明涉及孔隙裂缝或裂缝性地层的渗透率定量计算，确切地说涉及一种利用测井渗透率进行地层有效裂缝的识别方法，属于地层物性评价范畴。

背景技术：

岩层是否具有渗透性以及渗透能力的大小，是油气田能否形成产能和产能大小的重要因素，对油气田开发具有重要意义。目前，渗透率的预测手段通常为实验室岩心测定和测井资料计算求取。实验室测定的岩心渗透率，是基于达西定律，以渗滤流体对岩样进行实验的测量结果。这种测量手段尺度较微观，成本较高且受限于样品采集，需采集的岩心样品数足够多时，实验室的分析结果才有可能接近实际储层的渗透率。因此，在实际的储层评价中通常采用测井手段来估算纵向上连续的储层渗透率。

如公开号为102507412b,公开日为2014年7月2日的中国专利文献公开了一种碳酸盐岩油藏等效模型的裂缝-基质渗透率级差判别方法，包括：等效裂缝单一介质数值模拟的裂缝-基质渗透率级差判别；等效基质单一介质数值模拟的裂缝-基质渗透率级差判别；等效双孔单渗数值模拟的裂缝-基质渗透率级差判别。本发明能够快速实现储层类型多样、裂缝与基质搭配关系复杂、渗透率级差变化大、油气水关系复杂、压力分布变化大、模拟区块大、生产史复杂等各类碳酸盐岩油气藏的历史拟合和方案预测。

由测井手段预测渗透率，是一种岩石物理学的概念，通常基于建立区域内测井参数与储层渗透率（通常由实验室测定）间的经验关系进行计算。目前在孔隙-裂缝性储层系统中，通常将储层的渗透率分为孔隙部分的渗透率和裂缝部分的渗透率来考虑。使用上述方法准确预测渗透率的前提是预知该段的孔隙构成究竟是孔隙还是裂缝，而在实际的计算过程中，这是难以实现的，因此对油气田产能的评估和实际开发都造成了十分被动的影响。或者使用核磁共振特殊测井来计算渗透率，然而这依旧是基于孔隙度的算法，其局限性是当地层孔隙特征不明显的时候很难准确计算。

技术实现要素：

本发明旨在针对上述现有技术所存在的缺陷和不足，提供一种利用测井渗透率进行地层有效裂缝的识别方法，本方法切实可行地解决了无法预判地层中是“孔”还是“缝”所造成的被动问题，极大的优化了油气田产能评估流程，提高了油气田开发效率，对推进储层渗透率预测技术的进程具有革新性的意义。

本发明是通过采用下述技术方案实现的：

一种利用测井渗透率进行地层有效裂缝的识别方法，其特征在于：首先根据钻井液中的固相颗粒与液相滤液侵入地层的深度，判断地层的渗透性，并由实际工况得到流体流量q，结合横截面积a、流体渗滤路径l、压差δp和流体粘度μ四项参数，根据达西定律计算出储层的渗透率：

式中，

k----渗透率，μm²；

q----流体流量，cm³/s；

a----垂直于流体流动方向岩石横截面积cm²；

l----流体渗滤路径，cm；

----压差，pa；

----流体粘度，mpa·s；

根据计算出的渗透率，识别地层的有效裂缝。

所述流体流量q的计算方法如下：

首先利用体积模型法计算侵入钻井液体积，采用流体替换方法计算钻井液侵入体积,选用pe曲线来进行流体替换差值计算:

（1）

式中，

pe原----原始状态下理论岩心密度值，b/e；

pe骨架----各骨架矿物的岩性密度值，b/e；

v总----孔隙和矿物总百分含量，数值为100；

v骨架----各骨架矿物对应的体积百分比，%，测井计算求得；

pe黏土----各黏土矿物对应的体积百分比，b/e；

v黏土----各黏土矿物对应的体积百分比，%，测井计算求得；

pe储层流体----原状地层连通孔隙中流体的岩性密度值，b/e；

pe束缚流体----非连通孔隙中流体的岩性密度值，b/e；

连通----连通孔隙度，测井计算求得，%；

非连通----非连通孔隙度，测井计算求得，%；

pe钻井液----钻井液的pe值，b/e，根据钻井液中所加重矿物含量计算得到，或直接测量；

公式（1）表示当地层未被钻开时，原始状态下的岩性密度理论值；

（2）

式中，

pe测----实际测量岩性密度值，b/e；

----侵入钻井液所占孔隙度，%；

公式（2）表示当地层钻开后，部分连通孔隙和裂缝中流体被钻井液替换后的实际测量的岩性密度值；

（3）

式中，

侵入----地层被钻开前后岩性密度变化值δ侵入，b/e；

式（3）表示由测井仪器实测得到的岩性密度值pe测减去原始地层状态下的岩性密度值pe原，将得到地层被钻开后钻井液部分或完全侵入时的连通孔隙中和裂缝中岩性密度的变化值δ侵入；将（1）（2）式带入（3）式得到：

（4）

通过变换得到：

（5）

公式（5）代表钻井液侵入连通孔隙和裂缝的等效孔隙度，即侵入钻井液的等效百分体积；

测得岩心物性分析岩样质量m，根据体积公式：

（6）

m----岩心物性分析岩样质量，g；

ρ----测井测得该深度岩样的密度值，g/cm3

v----该深度岩样的实际体积，cm3；

而该一深度段某一种矿物的实际体积v实应为：

（7）

v百分含量----为该矿物这一深度段所占百分体积，%；

v实----该一深度段某一种矿物的实际体积，g；

设百分体积与实际体积之间关系为α，表达为：

（8）

将公式（6）代入公式（8），可得转换系数：

将侵入钻井液的等效百分体积乘以转换系数，即可得到侵入钻井液等效体积：

（9）

式中，

v钻井液----侵入钻井液等效体积，cm³；

由于钻井液主要是固相颗粒反应pe值，因此式（9）计算得到的是固相颗粒的等效钻井液体积v钻井液，而实际滤液体积为：

（10）

v滤液----实际侵入钻井液体积，cm³；

c钻井液----钻井液固相颗粒含量浓度，%，（实际采集获得）；

把某一深度点总浸泡时间分为三部分：钻进时、完钻后等待测井时，测井时：

（11）

t总----某一深度所测得资料的总浸泡时间，s；

t进----某一深度钻进结束时浸泡时间，s；

t等----完钻到测井开始时间，s，可采集；

t测----测井开始到测得该点所耗时间，s，可采集；

钻进时，

（12）

t钻进----钻进总耗时，s；

t钻遇----钻遇致该深度点耗时，s，钻时曲线计算获得；

将时间与深度对应、深度与曲线对应，最后流体流量曲线q为：

（13）

v路径----残留在渗滤路径中的钻井液体积，cm³

q----通过岩样的流体流量等于进入的流体体积减去残留在路径中的流体体积的差值与流体穿过岩样的总时间的比值。

所述的渗滤路径l选择与实验室岩样相同长度为渗滤路径l。

所述的横截面积a的计算方法为：

（16）

式中：

r----钻头半径，cm。

所述的压差δp的计算方法为：

压差的计算分为钻进、等待和测井状态下的压差；

钻进时：

（17）

式中：

p进----某一深度点钻进时对井壁的压力，pa；

ρ钻井液----钻井液密度，g/cm³；

h----当前深度点，m；

g----重力加速度，m/s²；

p泵----泵压，pa；

p地层----地层压力，pa。

地层压力需实测或选用区域地层压力；

等待压差和测井状态下压差相等：

（18）

式中：

p测–等待和测井时钻井液对井壁的压力，pa；

p地层----地层压力，pa。

与现有技术相比，本发明所达到的有益效果如下：

本发明首次提出一种基于达西定律和钻井液侵入体积计算渗透率的方法，切实可行的解决了无法预判地层中是“孔”还是“缝”所造成的被动问题，极大的优化了油气田产能评估流程，提高了油气田开发效率，对推进储层渗透率预测技术的进程具有革新性的意义。

附图说明

下面将结合说明书附图和具体实施方式对本发明作进一步的详细说明，其中：

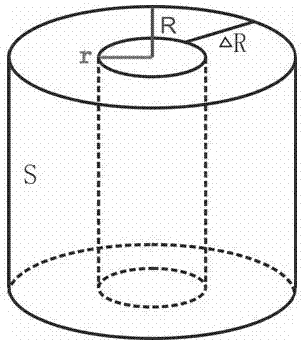
图1为井筒渗滤路径示意图；

图2为基于达西定律和钻井液侵入体积测井渗透率计算流程示意图。

具体实施方式

作为本发明的最佳实施方式，其公开了一种利用测井渗透率进行地层有效裂缝的识别方法，在裂缝--孔隙性储层中，当地层被钻开时，在井筒压力与地层压力压差作用下钻井液势必会侵入地层。根据达西定律，渗透率的表达式为：

式中，

k----渗透率，μm²；

q----流体流量，cm³/s；

a----垂直于流体流动方向岩石横截面积cm²；

l----流体渗滤路径，cm；

----压差，pa；

----流体粘度，mpa·s。

在实际计算中，流体粘度为钻井液粘度，可直接获取；流体流量q、地层压差δp、横截面积a和渗滤路径l则需通过计算求得。

由于孔隙—裂缝型储层主要的流动通道为裂缝，钻井液中的固相颗粒与液相滤液即可随裂缝侵入地层，又因裂缝—孔隙型储层的有效流动截面远大于孔隙型储层，因此钻井液中的固相颗粒又可继续沿裂缝深入到储层内部，且固相颗粒的侵入深度与液相滤液呈正相关性。再者，岩性密度曲线（pe）受钻井液中固相颗粒浓度影响最大，如钻井液中加有固相颗粒的重晶石，其pe值将远大于地层岩性的标准pe值，因此可基于重晶石的渗入，确定地层渗透性。在此基础之上，结合实际工况得到流体流量q（cm3/s），结合横截面积a（cm2）、流体渗滤路径l（cm）、压差δp（pa）和流体粘度μ（mpa·s）四项参数，即可得到最终的地层渗透率。

计算流程如下：

（1）流体流量计算（q）

首先利用体积模型法计算侵入钻井液体积。认为地层由骨架矿物、黏土矿物和孔隙组成。在地层被钻开前，孔隙中都充填的为地层原状流体，在地层被钻开后，连通孔隙和裂缝中的可流动流体被替换或部分替换为钻井液，而非连通孔隙中的流体依旧为原流体，因此采用此流体替换方法即可计算钻井液侵入体积。在此选用对钻井液敏感性相对较高的pe曲线来进行流体替换差值计算。

（1）

式中，

pe原----原始状态下理论岩心密度值，b/e；

pe骨架----各骨架矿物的岩性密度值，b/e；

v总----孔隙和矿物总百分含量，数值为100。

v骨架----各骨架矿物对应的体积百分比，%，测井计算求得；

pe黏土----各黏土矿物对应的体积百分比，b/e；

v黏土----各黏土矿物对应的体积百分比，%，测井计算求得；

pe储层流体----原状地层连通孔隙中流体的岩性密度值，b/e；

pe束缚流体----非连通孔隙中流体的岩性密度值，b/e；

连通----连通孔隙度，测井计算求得，%；

非连通----非连通孔隙度，测井计算求得，%；

pe钻井液----钻井液的pe值，b/e，可根据钻井液中所加重矿物含量计算得到，或直接测量。

公式（1）表示当地层未被钻开时，原始状态下的岩性密度理论值。

（2）

式中，

pe测----实际测量岩性密度值，b/e；

----侵入钻井液所占孔隙度，%；

公式（2）表示当地层钻开后，部分连通孔隙和裂缝中流体被钻井液替换后的实际测量的岩性密度值。

（3）

式中，

侵入----地层被钻开前后岩性密度变化值δ侵入，b/e。

式（3）表示由测井仪器实测得到的岩性密度值pe测减去原始地层状态下的岩性密度值pe原，将得到地层被钻开后钻井液部分或完全侵入时的连通孔隙中和裂缝中岩性密度的变化值δ侵入。将（1）（2）式带入（3）式得到：

（4）

通过变换得到：

（5）

公式（5）代表了钻井液侵入连通孔隙和裂缝的等效孔隙度，即侵入钻井液的等效百分体积。

测得岩心物性分析岩样质量m，根据体积公式：

（6）

m----岩心物性分析岩样质量，g；

ρ----测井测得该深度岩样的密度值，g/cm3

v----该深度岩样的实际体积，cm3。

而该一深度段某一种矿物的实际体积v实应为：

（7）

v百分含量----为该矿物这一深度段所占百分体积，%。

v实----该一深度段某一种矿物的实际体积，g。

设百分体积与实际体积之间关系为α，可表达为：

（8）

将公式（6）代入公式（8），可得转换系数：

将侵入钻井液的等效百分体积乘以转换系数，即可得到侵入钻井液等效体积：

（9）

式中，

v钻井液----侵入钻井液等效体积，cm³。

由于钻井液主要是固相颗粒反应pe值，因此式（9）计算得到的是固相颗粒的等效钻井液体积v钻井液，而实际滤液体积为：

（10）

v滤液----实际侵入钻井液体积，cm³；

c钻井液----钻井液固相颗粒含量浓度，%，（实际采集获得）。

因为在地层钻开的瞬间，就会发生钻井液侵入，因此越晚钻开的地层，钻井液浸泡时间越短。且浸泡时间与钻时、完钻到测井开始间隔时间和测井测量速度有关，因此根据实际情况，把某一深度点总浸泡时间分为三部分：钻进时、完钻后等待测井时，测井时：

（11）

t总----某一深度所测得资料的总浸泡时间，s；

t进----某一深度钻进结束时浸泡时间，s；

t等----完钻到测井开始时间，s，可采集；

t测----测井开始到测得该点所耗时间，s，可采集。

钻进时，

（12）

t钻进----钻进总耗时，s；

t钻遇----钻遇致该深度点耗时，s，钻时曲线计算获得。

将时间与深度对应、深度与曲线对应，最后流体流量曲线q为：

（13）

v路径----残留在渗滤路径中的钻井液体积，cm³

q----通过岩样的流体流量（等于进入的流体体积减去残留在路径中的流体体积的差值与流体穿过岩样的总时间的比值）。

（2）渗滤路径（l）

实验室测量岩样渗透率中，渗滤路径长度近似选用岩样长度，在此选择与实验室岩样相同长度为渗滤路径l

图1为井筒渗滤路径示意图，r为钻头半径，△r为渗滤路径。

（3）横截面积（a）计算

由于井筒是向外放射的，所以常规计算的井下钻井液横向通过井壁横截面积不同于实验室测量，而是随着侵入深度的加深，横截面积也增大，即为：

（16）

式中：

r----钻头半径，cm。

（4）压差（δp）计算

压差的计算分为钻进、等待和测井状态下的压差。钻进时：

（17）

式中：

p进----某一深度点钻进时对井壁的压力，pa；

ρ钻井液----钻井液密度，g/cm³；

h----当前深度点，m；

g----重力加速度，m/s²；

p泵----泵压，pa；

p地层----地层压力，pa。

地层压力需实测或选用区域地层压力。

等待压差和测井状态下压差相等：

（18）

式中：

p测–等待和测井时钻井液对井壁的压力，pa；

p地层----地层压力，pa。

在通过上述步骤求得流体流量q、地层压差δp、横截面积a和渗滤路径l后，再通过实际测量获取粘度，即可根据达西定律求得储层段的渗透率。