基于底面两圈标准差多项式模型的粮仓检测方法及系统与流程

本发明涉及一种基于底面两圈标准差多项式模型的粮仓检测方法及系统，属于传感器与检测技术领域。

背景技术：

粮食安全包括数量安全和原粮安全。粮食数量在线检测技术与系统研究应用是国家粮食数量安全的重要保障技求，开展这方面的研究与应用事关国家粮食安全，具有重要的意义，并将产生巨大的社会经济效益。

由于粮食在国家安全中的重要地位，要求粮食数量在线检测准确、快速和可靠。同时由于粮食数量巨大，价格低，要求粮食数量在线检测设备成本低、简单方便。因此检测的高精度与检测系统的低成本是粮食数量在线检测系统开发必需解决的关键课题。

授权公告号为cn105403294b的中国发明专利文件公开了一种基于多项式展开的粮仓储粮重量检测方法及其装置。该发明专利涉及基于多项式展开的粮仓储粮重量检测方法及其装置。依据粮仓储粮重量的理论检测模型，建立基于多项式展开的粮仓储粮重量检测模型，利用基于回归和多项式最大阶数选择样本集的多项式最大阶数优化方法对模型参数进行优化。

该方案提高了储粮重量(即储量数量)的检测精确度，还具有较强适应性和鲁棒性。然而，由于粮食的存储性质和传感器精度的限制，储粮数量的检测精度还有待进一步提高。

技术实现要素：

本发明的目的是提供一种基于底面两圈标准差多项式模型的粮仓检测方法及系统，以解决如何在现有技术基础上进一步提高检测精确度的问题。

为实现上述目的，本发明的方案包括：

本发明的一种基于底面两圈压力传感器的粮仓储粮检测方法，包括如下步骤：

1)检测粮仓底面设置的内外两圈压力传感器的输出值；

2)利用两圈压力传感器输出值均值估计粮堆底面压强均值构建与的关系；

3)利用两圈压力传感器输出值均值估计粮堆高度h，构建与h的关系；

4)利用估计项im(s)估计粮堆侧面单位面积平均摩擦力构建外圈压力传感器输出值均值内圈压力传感器输出值均值外圈压力传感器输出值标准差sd(souter)、内圈压力传感器输出值标准差sd(sinner)与im(s)的关系：

其中，kx为设定的系数；当对应粮堆的散落性小于设定标准时，对应的当对应粮堆的散落性大于等于设定标准时，对应的

5)将步骤2)、3)、4)得到的关系代入粮仓储粮数量理论检测模型得出粮仓储粮数量与sd(souter)、sd(sinner)关系的检测模型，进而根据步骤1)检测的两圈压力传感器的输出值得出粮仓储粮数量其中，kc＝cb/ab，ab为粮堆底面面积，cb为粮堆底面周长。

进一步的，步骤1)中，还对压力传感器的输出值进行筛选，筛选方法为：仅保留与该圈压力传感器输出值的平均值的差在设定范围内的输出值；所述压力传感器输出值的平均值为传感器输出值的中值及其相邻设定数量的输出值的平均值。

进一步的，若内圈压力传感器输出值满足则去除该传感器输出值，得到去除后的内圈压力传感器输出值序列qbs(sinner(i))；其中，qb(sinner(i))为第i个内圈压力传感器输出值，为内圈压力传感器输出值中值及相邻设定数量的输出值的均值，sdmed(sinner)为内圈压力传感器输出值标准差，tsd为内圈压力传感器点去除阈值系数。

进一步的，若外圈压力传感器输出值满足则去除该传感器输出值，得到去除后的外圈压力传感器输出值序列qbs(souter(i))；其中，qb(souter(i))为第i个外圈压力传感器输出值，为外圈压力传感器输出值中值及相邻设定数量的输出值的均值，sdmed(souter)为外圈压力传感器输出值标准差，ctsd为外圈压力传感器点去除阈值系数。

进一步的，两圈压力传感器输出值均值的计算方法为：

其中，为qbs(sinner(i))的均值，为qbs(souter(i))的均值。

进一步的，步骤2)中，与的关系为：

其中，为的估计，bb(m)为估计项的系数，nb为估计的多项式阶数，m＝0,...,nb；

步骤3)中，与h的关系为：

其中，为h的估计，bh(j)为h估计项的系数，nh为h估计的多项式阶数，j＝0,...,nh；

步骤4)中，与sd(souter)、sd(sinner)的关系为：

其中，为的估计，bf(n)为估计项的系数，nf为估计的多项式阶数，n＝0,...,nf；

步骤5)中得出粮仓储粮数量为：

进一步的，还包括步骤6)，步骤6)包括整理步骤5)中的检测模型，限制项的最大阶数为nb，限制im(s)项的最大阶数为nf，得出：

其中，ab(m)、af(n,m)为估计项的系数。

进一步的，整理步骤6)中的检测模型，对第二项按与im(s)乘积项的阶数和nn+m的升序排序，nn+m按im(s)阶数由低到高排序，得出：

其中，nn+m为检测模型第二项中与im(s)乘积项的阶数和，取值区间为[1,nb+nf]；

进一步的，步骤4)中：

当时，对应的

当时，对应的

其中，ksd为预设调整系数。

本发明的一种基于底面两圈压力传感器的粮仓储粮检测系统，包括处理器，所述处理器用于执行实现上述方法的指令。

本发明的有益效果为：

本发明根据粮仓压强分布特点，提出了一种采用基于底面两圈压力传感器输出值标准差的粮仓储粮数量检测模型的粮仓储粮重量检测方法，本方案相比现有技术进一步提高了检测精度，鲁棒性更强，适应多种类型的粮仓结构，同时进一步减少了传感器的使用，降低了系统成本和运维费用。

附图说明

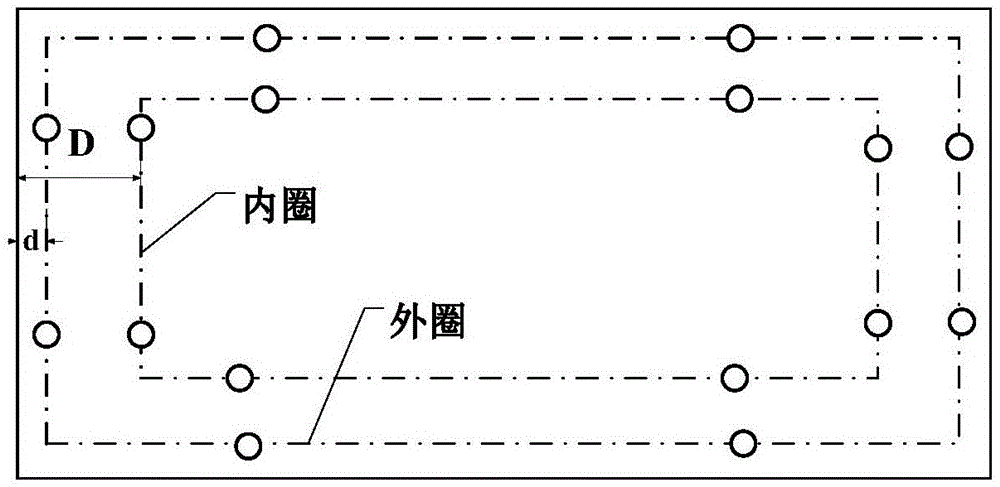
图1是平房仓底面压力传感器布置模型示意图；

图2是筒仓底面压力传感器布置示意图；

图3是不同粮仓外圈压力传感器输出值分布示意图；

图4是不同粮仓内圈压力传感器输出值分布示意图；

图5是选择后内圈压力传感器输出值分布示意图；

图6是实施例1的利用所有样本建模的粮仓储粮重量计算误差示意图；

图7是实施例1的7至12号样本作为测试样本时粮仓储粮重量计算误差示意图；

图8是实施例1的建模样本的粮仓储粮重量计算误差示意图；

图9是实施例1的所有样本的粮仓储粮重量计算误差示意图；

图10是实施例1、2的本发明的粮仓储粮数量检测方法流程图；

图11是实施例2的利用所有样本建模的粮仓储粮重量计算误差示意图；

图12是实施例2的7至12号样本作为测试样本时粮仓储粮重量计算误差示意图；

图13是实施例2的建模样本的粮仓储粮重量计算误差示意图；

图14是实施例2的所有样本的粮仓储粮重量计算误差示意图。

具体实施方式

本发明提供了一种基于底面两圈压力传感器的粮仓储粮检测系统，该系统包括处理器，该处理器用于执行指令实现本发明的基于底面两圈压力传感器的粮仓储粮检测方法，下面结合附图对该方法做进一步详细说明。

实施例1

1.检测理论模型

通过粮堆受力分析可以推出，粮仓储粮数量理论检测模型为：

其中，ab为粮堆底面面积，kc为模型参数，kc＝cb/ab，cb为粮堆底面周长，h为粮堆高度，ff为粮堆侧面与粮仓侧面之间的平均摩擦系数，为对底面压强均值，为粮堆侧面压强均值，令：

其中，为粮堆侧面单位面积平均摩擦力。则有：

由式(3)可以看出，粮堆重量与且仅与粮堆底面压强均值侧面单位面积平均摩擦力以及粮堆高度h有关。因此基于压力传感器的粮仓储粮数量检测的核心在于和h三参数的检测与估计。

2.传感器布置模型

对于通常使用的平房仓和筒仓，在粮仓底面按外圈和内圈两圈布置压力传感器，如图1和图2所示，圆圈为压力传感器布置位置。外圈压力传感器均与侧面墙距离为d，内圈压力传感器均与侧面墙距离为d。可取d＞0米且d＜1米，取d＞2米，一般取d为3米左右。为了保证检测模型的通用性，各粮仓的内外两圈压力传感器与侧面墙距离d和d应相同。两圈压力传感器个数均为6-10，传感器间距应大于1m。

3.传感器选择与标准差计算

由于粮食的有限流动性，内外两圈压力传感器输出值具有显著的波动性和随机性，当内外两圈压力传感器数量足够多时，传感器输出值呈近似正态分布。由于检测系统成本问题，内外两圈压力传感器数量较少。在这种情况下，压力传感器输出值的波动性与随机性势必严重影响外圈压力传感器输出值均值与标准差的准确估算。图3、图4为不同粮仓内外两圈压力传感器输出值依大小排序后的分布情况。从这些测量结果可以看出，在中值附近区域传感器输出值变化与随机性相对较小，而在较小和较大值的区域输出值变化与随机性相对较大。较小和较大值的区域输出值的随机性大势必严重影响内外两圈压力传感器输出值均值与标准差的准确估算。因此，应合理去除较小和较大值的区域输出值点。下面讨论内外两圈压力传感器输出值均值与标准差的计算方法。

3.1内圈压力传感器选择与标准差计算

对于内圈压力传感器输出值序列qb(sinner(i))，i＝1,2,...,ni，ni为内圈压力传感器个数。对传感器输出值序列依大小排序，求出中值点。取中值点左边相邻nlm个输出值点，取中值点右边相邻nrm个输出值点，形成中值邻近点的传感器输出值序列qmed(sinner(i))。一般取nlm＝2-3，nrm＝2-3。求出所选取中值邻近点的传感器输出值序列qmed(sinner(i))的均值

由内圈压力传感器输出值序列qb(sinner(i))和均值计算内圈压力传感器输出值标准差sdmed(sinner)：

其中，为内圈中值点两边邻近输出值点均值。

内圈压力传感器输出值点去除规则为：

若则去除qb(sinner(i))点(6)

其中，tsd为内圈压力传感器点去除阈值系数，可根据粮仓储粮数量检测模型的误差变化而合理调整。

式(6)所示的内圈压力传感器输出值点去除规则，基于中值点两边邻近输出值点均值的标准差sdmed(sinner)，以消除较小和较大值的区域输出值随机性的影响，并实现内圈压力传感器输出值点去除门限的自适应调整，内圈压力传感器输出值标准差sdmed(sinner)大，则输出值点去除门限增大，反之亦然。同时引入基于粮仓储粮数量检测模型的误差变化的内圈压力传感器点去除阈值系数tsd，以实现内圈压力传感器输出值点去除门限的合理调整与优化。图5为基于式(6)所示的内圈压力传感器输出值点去除规则，去除较小和较大值的区域部分输出值点后，内圈压力传感器输出值依大小排序后的分布情况。可以看出，合理去除了较小和较大值的区域输出值。

对于内圈压力传感器输出值序列qb(sinner(i))，i＝1,2,...,ni，根据式(6)所示的内圈压力传感器输出值点去除规则，去除满足规则的传感器输出值点后，形成去除后的内圈压力传感器输出值序列qbs(sinner(i))，i＝1,2,...,nis，nis为去除后内圈压力传感器输出值序列数据个数。则内圈压力传感器输出值均值为：

式(5)为内圈压力传感器输出值标准差计算公式，式(7)为内圈压力传感器输出值均值计算公式。这种内圈压力传感器输出值均值和标准差计算方法的主要特点在于通过去除较小和较大值的区域输出值点，以减少传感器输出值随机性对内圈压力传感器输出值均值和标准差计算的影响。

3.2外圈压力传感器选择与标准差计算

采用同样的方法，对于外圈压力传感器输出值序列qb(souter(i))，i＝1,2,...,no，no为外圈压力传感器个数。对输出值序列依大小排序，求出中值点。取中值点左边相邻nlm个输出值点，取中值点右边相邻nrm个输出值点，一般取nlm＝2-3，nrm＝2-3，形成中值邻近点的传感器输出值序列qmed(souter(i))。求出所选取传感器输出值序列qmed(souter(i))的均值

由外圈压力传感器输出值序列qb(souter(i))和均值计算外圈压力传感器输出值标准差sdmed(souter)：

其中，为外圈中值点两边邻近输出值点均值。

则外圈压力传感器输出值点去除规则为：

若则去除qb(souter(i))点(10)

其中，ctsd为外圈压力传感器点去除阈值系数，可根据粮仓储粮数量检测模型的误差变化而合理调整。此处采用ctsdtsd作为外圈压力传感器输出点去除阈值系数，以便于系数ctsd的选择与优化。

对于外圈压力传感器输出值序列qb(souter(i))，i＝1,2,...,no，根据式(10)所示的外圈压力传感器输出值点去除规则，去除满足规则的传感器输出值点后，形成去除后的外圈压力传感器输出值序列qbs(souter(i))，i＝1,2,...,nos，nos为去除后外圈压力传感器输出值序列数据个数。则外圈压力传感器输出值均值为：

式(9)为外圈压力传感器输出值标准差计算公式，式(11)为外圈压力传感器输出值均值计算公式。

4.模型项构造

根据图1、图2所示的粮仓底面两圈压力传感器布置模型，对于由式(5)所示的内圈压力传感器输出值标准差计算公式、式(7)所示的内圈压力传感器输出值均值计算公式以及式(9)所示的外圈压力传感器输出值标准差计算公式、式(11)所示的外圈压力传感器输出值均值计算公式，令：

其中，为内外两圈压力传感器输出值均值。

对于式(3)所示的粮仓储粮数量理论检测模型，根据粮仓的特性，显然有：

因此，可以利用构造粮堆底面压强和粮堆高度h的估计。

由实验结果可知，由于侧面单位面积平均摩擦力作用，势必导致内外两圈压力传感器输出值均值、标准差的变化，增大势必使内外两圈压力传感器输出值均值、标准差的差别程度增大。因此内外两圈压力传感器输出值均值的差、以及标准差的大小可以体现的大小，可以利用这些量构造侧面单位面积平均摩擦力的估计。令：

其中，im(s)为基于内外两圈压力传感器输出值标准差均值的粮堆侧面单位面积平均摩擦力的估计项。通过引入了常数项使式(15)中的预设调整系数ksd取值接近于1，便于ksd值选择。显然，式(15)的第一项体现了粮堆侧面单位面积平均摩擦力对内外两圈压力传感器输出值均值的影响，第二项体现了对内外两圈压力传感器输出值标准差的影响。式(15)针对的是稻谷等流动性较低的粮堆，而针对小麦等流动性较强的粮堆，可参考实施例2中的式(34)来得到粮堆侧面单位面积平均摩擦力的估计项。

粮食的流动性又称粮食的流散特性，粮食的流散特性主要包括散落性、自动分级、孔隙度等，这是颗粒状粮食所固有的物理性质。粮食在自然形成粮堆时，向四面流动成为一个圆锥体的性质称为粮食的散落性。粮粒的大小、形状、表面光滑程度、容量、杂质含量都对粮食的散落性有影响。粒大、饱满、圆型粒状、比重大、表面光滑、杂质少的粮食散落性好，反之则散落性差。不同粮食之间，上述外观特征明显不同，因此，具有不同的散落特性。

粮食散落性的好坏通常用静止角表示。静止角是指粮食由高点落下，自然形成圆锥体的斜面与底面水平线之间的夹角。静止角与散落性成反比，即散落性好(相当于散落性大于等于设定标准)，静止角小；散落性差(相当于散落性小于设定标准)，静止角大。表a中给出了主要粮种静止角的大小。

表a几种常见粮食的静止角大小(单位：度)

当粮堆静止角小于40度时，采用本实施例的式(15)来计算估计项(即im(s))，当粮食静止角大于等于40度时，采用实施例2的式(34)来计算估计项(即id(s))，此处静止角指的是粮食品种对应的最大静止角(即为表a中的静止角止)。

5.检测模型

对于式(3)所示的粮仓储粮数量理论检测模型，采用im(s)多项式构建和h的估计为：

其中，bb(m)、bh(j)、bf(n)分别为h和估计项的系数，m＝0,...,nb，j＝0,...,nh，n＝0,...,nf，nb、nh、nf分别为h和估计的多项式阶数。将式(16)至式(18)代入式(3)，则有：

整理式(19)，并限制项的最大阶数为nb，限制im(s)项的最大阶数为nf，可以得出：

其中，ab(m)、af(n,m)为估计项的系数，m＝0,...,nb，n＝1,...,nf，nb、nf分别为im(s)项的阶数。显然，式(20)的第一项总项数为nb+1，最大阶数为nb；第二项总项数为(nb+1)nf，与im(s)乘积项的最大阶数和为nb+nf。为了限制式(20)所示检测模型的非线性程度，应控制第二项中乘积项最大阶数和。因此，为了便于模型总项数优化，整理式(20)，对第二项按与im(s)乘积项的阶数和nn+m的升序排序，nn+m相同时按im(s)阶数由低到高排序，则有：

其中，nn+m为检测模型第二项中与im(s)乘积项的阶数和，取值区间为[1,nb+nf]；mb、me取值如下二式所示：

显然，式(21)第二项的乘积项总数为(nb+1)nf，模型项总数nitem的最大值为nb+(nb+1)nf+1。为了限制式模型的非线性程度，可从模型尾部(第nb+(nb+1)nf+1乘积项)项开始，去除若干乘积项项，以减少模型项总数nitem。

式(21)为基于底面两圈压力传感器和im(s)的多项式粮仓储粮数量检测模型。根据im(s)项的特点，该模型适用于小麦等流动性较高的粮食粮仓储粮数量检测。

6.建模方法

对于式(21)所示的基于底面两圈压力传感器和im(s)的多项式粮仓储粮数量检测模型，由式(4)至(23)可以看出，式(21)所示的粮仓储粮数量检测模型建模参数包括项的最大阶数nb、im(s)项的最大阶数nf、模型项总数nitem、im(s)项参数ksd、内圈压力传感器点去除阈值系数tsd、外圈压力传感器点去除阈值系数ctsd以及多项式项系数ab(m)和af(n,m)等建模参数。令：

cr＝(nb,nf,nitem,ksd,tsd,ctsd)(24)

其中，cr为参数组。

从式(21)可以看出，若给定参数组cr的取值，则ab(m)和af(n,m)可利用多元线性回归方法获得。因此参数组cr优化问题是式(21)建模的关键问题。

对于给定的样本集其中，k为样本点号，k＝1,2,3,...,m，m为样本个数；为第k个样本点的内圈压力传感器输出值序列，i＝1,2,...,ni，ni为内圈压力传感器个数；为第k个样本点的外圈压力传感器输出值序列，j＝1,2,...,no，no为外圈压力传感器个数；w^k为样本点k的实际进粮重量，为相应的粮仓底面面积。将样本集s分为三个部分，分别作为多元回归样本集sm、参数优化样本集so与测试样本集st。通过多元回归样本集sm样本与参数优化样本集so样本的不同，以避免模型过学习，提高模型的泛化能力。当样本数小时，将样本集s分为两个部分，一部分同时作为多元回归样本集sm和参数优化样本集so，另外一部分作为测试样本集st。

式(21)所示的基于底面两圈压力传感器和im(s)的多项式粮仓储粮数量检测模型建模优化可表示为下式所示的百分比误差的最小化问题：

其中，e(cr,ab(m),af(n,m))为建模优化误差；参数组cr以及ab(m)和af(n,m)为优化参数；为式(21)所示的样本点k的粮仓储粮数量检测模型的粮堆重量计算值；w^k为样本点k的实际储粮重量。实际优化计算表明，由于参数组cr的特性，使得式(25)成为很强的非凸的最优化问题。下面讨论具体优化方法。

通过分析可以看出，可将式(21)所示的基于底面两圈压力传感器和im(s)的多项式粮仓储粮数量检测模型建模优化问题分解为两个优化问题。

第一个优化问题是给定参数组cr具体取值的多元线性回归问题，回归误差模型如下式所示：

其中，为给定参数组cr的样本点k的粮仓储粮数量检测模型的计算值，粮仓储粮数量检测模型如式(21)所示；er(cr)为回归百分比误差。

第二个优化问题是基于式(26)多元线性回归的参数组cr中所有参数的优化问题，如下式所示：

其中，为给定参数组cr具体取值，通过式(26)的多元线性回归获得ab(m)和af(n,m)的最优值；为基于给定cr以及的样本点k的粮仓储粮数量检测模型的计算值，粮仓储粮数量检测模型如式(21)所示；e(cr)为cr优化误差。

因此，可以看出，对于式(21)所示的基于底面两圈压力传感器和im(s)的多项式粮仓储粮数量检测模型建模优化问题，可以通过上述两个优化问题的结合来实现。由于式(27)具有很强的非凸的最优化特性，本研究采用可行域内全局搜索方法实现参数组cr中的参数的优化。下面讨论的具体的优化方法。

设定nb取值范围为[1,maxnb]，nf取值范围为[1,maxnf]，模型项总数nitem选择范围为[1,nb+(nb+1)nf]。ksd取值范围为[0,maxksd]，tsd取值范围为[mintsd,maxtsd]，ctsd取值范围为[minctsd,maxctsd]。一般取mintsd和minctsd为0.4，取maxnb和maxnf为6，取maxksd和maxtsd为4，取maxctsd为2。对于各参数取值范围，按一定间隔均匀选取若干个取值点，由这些取值点的不同组合，可构建参数组cr的不同取值，并由参数组cr的不同取值构成cr的取值集合对于集合的任一元素其中为集合第i个元素的参数nb、nf、nitem、ksd、tsd、ctsd的相应取值，为集合中元素个数，利用式(26)所示优化模型优化，并使：

其中，为参数组cr在集合所有元素中的最优值；为集合第i个元素相应的ab(m)和af(n,m)的最优值。

具体的优化算法如算法1所示。

算法1基于底面两圈压力传感器和im(s)的多项式粮仓储粮数量检测模型建模优化算法

输入：参数组cr的各参数取值点个数与取值；

参数优化样本so和多元回归样本集sm。

输出：参数组cr的各参数以及回归系数ab(m)和af(n,m)的最优值。

1.由参数组cr的各参数的不同取值组合构造取值集合

2.i＝1。

3.若则转5，否则从取值集合中按顺序取出第i组取值组合i＝i+1。

4.对于取值组合利用式(26)进行多元线性回归，求出取值组合相应ab(m)和af(n,m)的最优值并由式(27)求出取值组合相应的优化误差保存取值组合以及相应的和转3。

5.若则输出以及相应的最优值并退出。

上述利用多元回归样本集sm、参数优化样本集so进行建模的方法，将有助于降低式(21)所示模型的多项式最大阶数和模型项总数，有助于实现模型的结构风险最小化，提高模型的泛化能力。

计算机根据对压力传感器的检测结果及粮仓底面积的相关参数的采集，利用式(21)的模型，能够很容易的计算出对应粮仓的储粮数量。

7.检测实例与结果分析

7.1检测实例1

实验所采用的平房仓长9m，宽4.2m，面积为37.8m²，cb/ab＝0.698。粮仓均属于小型粮仓，cb/ab相对较大。根据图1所示的压力传感器布置模型，压力传感器分2圈布置，内圈6个，外圈16个，共22个压力传感器。小麦粮堆高度约6米，进粮时每1米取一次数据，重复5次实验共获得30个样本。

对于式(21)所示的基于底面两圈压力传感器和im(s)的多项式粮仓储粮数量检测模型，将全部30个样本作为建模样本。优化后的建模参数如表1所示，获得的参数如表2和3所示。粮仓储粮重量计算误差如图6所示，最大百分比误差为1.956e-5％。

表1优化后的建模参数

表2模型系数ab(m)

表3模型系数af(n,m)

表3(续)模型系数af(n,m)

对于式(21)所示的基于底面两圈压力传感器和im(s)的多项式粮仓储粮数量检测模型，以实验2的7至12号样本作为测试样本，利用实验3的13至18号样本作为参数优化样本，其余18个样本作为建模样本。优化后的建模参数如表4所示，获得的参数如表5和6所示。粮仓储粮重量计算误差如图7所示，最大测试百分比误差为2.29％。由于建模样本过少，使得最大测试误差较大，如果增大建模样本数量，则可进一步减少预测误差。

表4优化后的建模参数

表5模型系数ab(m)

表6模型系数af(n,m)

7.2检测实例2

对于山东齐河粮库、武汉粮库、广东新安粮库的3个小麦平房仓，储粮重量分别为2220.253吨、4441吨和3236吨。从检测数据中选取351个样本。取240个样本同时作为多元回归样本集和参数优化样本集，其它作为测试样本集。对于式(21)所示的基于底面两圈压力传感器和im(s)的多项式粮仓储粮数量检测模型，优化后的建模参数如表7所示，获得的参数如表8和9所示。建模样本的粮仓储粮重量计算误差如图8所示，所有样本的粮仓储粮重量计算误差如图9所示。从这些结果中可以看出，建模样本和测试样本的粮仓储粮重量计算误差均小于0.131％。

表7优化后的建模参数

表8模型系数ab(m)

表9模型系数af(n,m)

表9(续)模型系数af(n,m)

本发明所提出的基于底面两圈压力传感器输出值标准差的粮仓储粮数量检测模型与粮仓重量检测方法可按图10所示的实施方式实施，具体步骤实施如下：

(1)系统配置

选定具体压力传感器，并配置相应的数据采集、数据传输等系统。

(2)底面压力传感器安装

平房仓传感器布置如图1所示，筒仓如图2所示，底面压力传感器按外圈和内圈两圈布置，外圈压力传感器均与侧面墙距离为d＞0且d＜1米，内圈压力传感器均与侧面墙距离d＞2米。两圈压力传感器个数均为6-10，传感器间距应不小于1m。

(3)系统标定与模型建模

对于给定的传感器、粮食种类以及仓型，如果系统尚未有标定，则在多于6个粮仓中布置压力传感器，进粮至满仓，压力传感器输出值稳定后，采集各仓的压力传感器输出值，形成样本集其中，k为样本点号，k＝1,2,3,...,m，m为样本个数；为第k个样本点的内圈压力传感器输出值序列，i＝1,2,...,ni，ni为内圈压力传感器个数；为第k个样本点的外圈压力传感器输出值序列，j＝1,2,...,no，no为外圈压力传感器个数；w^k为样本点k的实际进粮重量，为相应的粮仓底面面积。

将样本集s分为三个部分，分别作为多元回归样本集sm、参数优化样本集so与测试样本集st。通过多元回归样本集sm样本与参数优化样本集so样本的不同，以避免模型过学习，提高模型的泛化能力。当样本数较少时，将样本集s分为两个部分，一部分同时作为多元回归样本集sm和参数优化样本集so，另外部分作为测试样本集st。

设定nb取值范围为[1,maxnb]，nf取值范围为[1,maxnf]，模型项总数nitem选择范围为[1,nb+(nb+1)nf]。ksd取值范围为[0,maxksd]，tsd取值范围为[mintsd,maxtsd]，ctsd取值范围为[minctsd,maxctsd]。一般取mintsd和minctsd为0.4，取maxnb和maxnf为6，取maxksd和maxtsd为4，取maxctsd为2。对于各参数取值范围，按一定间隔均匀选取若干个取值点，由这些取值点的不同组合，可构建参数组cr的不同取值，并由参数组cr的不同取值构成cr的取值集合按算法1所示的优化方法求出式(21)所示的粮仓储粮数量检测模型的所有参数。

算法1基于底面两圈压力传感器和im(s)的多项式粮仓储粮数量检测模型建模优化算法

输入：参数组cr的各参数取值点个数与取值；

参数优化样本so和多元回归样本集sm。

输出：参数组cr的各参数以及回归系数ab(m)和af(n,m)的最优值。

1.由参数组cr的各参数的不同取值组合构造取值集合

2.i＝1。

3.若则转5，否则从取值集合中按顺序取出第i组取值组合i＝i+1。

4.对于取值组合利用式(26)进行多元线性回归，求出取值组合相应ab(m)和af(n,m)的最优值并由式(27)求出取值组合相应的优化误差保存取值组合以及相应的和转3。

5.若则输出以及相应的最优值并退出。

(4)实仓重量检测

如果系统已标定，检测底面压力传感器输出值并利用式(21)所示模型进行粮仓储粮数量检测。

实施例2

1.检测理论模型

通过粮堆受力分析可以推出，粮仓储粮数量理论检测模型为：

其中，ab为粮堆底面面积，kc为模型参数，kc＝cb/ab，cb为粮堆底面周长，h为粮堆高度，ff为粮堆侧面与粮仓侧面之间的平均摩擦系数，为对底面压强均值，为粮堆侧面压强均值，令：

其中，为粮堆侧面单位面积平均摩擦力。则有：

由式(30)可以看出，粮堆重量与且仅与粮堆底面压强均值侧面单位面积平均摩擦力以及粮堆高度h有关。因此基于压力传感器的粮仓储粮数量检测的核心在于和h三参数的检测与估计。

2.传感器布置模型

对于通常使用的平房仓和筒仓，在粮仓底面按外圈和内圈两圈布置压力传感器，如图1和图2所示，圆圈为压力传感器布置位置，外圈压力传感器均与侧面墙距离为d，内圈压力传感器均与侧面墙距离为d。可取d＞0米且d＜1米，取d＞2米，一般取d为3米左右。为了保证检测模型的通用性，各粮仓的内外两圈压力传感器与侧面墙距离d和d应相同。两圈压力传感器个数均为6-10，传感器间距应大于1m。

3.模型项构造

对于图1、图2所示的粮仓底面两圈压力传感器布置模型，假设外圈压力传感器输出值均值为外圈压力传感器输出值标准差为sd(souter)，内圈压力传感器输出值均值为内圈压力传感器输出值标准差为sd(sinner)。令：

其中，为内外两圈压力传感器输出值均值。对于式(30)所示的粮仓储粮数量理论检测模型，根据粮仓的特性，显然有：

因此，可以利用构造粮堆底面压强和粮堆高度h的估计。

由实验结果可知，由于侧面单位面积平均摩擦力作用，势必导致内外两圈压力传感器输出值均值、标准差的变化，增大势必使内外两圈压力传感器输出值均值、标准差的差别程度增大。因此内外两圈压力传感器输出值均值的差、标准差的大小可以体现的大小，可以利用这些量构造侧面单位面积平均摩擦力的估计项im(s)，为了与实施例1相区别，本实施例中，估计项用id(s)表示，令：

其中，id(s)为基于内外两圈压力传感器输出值标准差之差的粮堆侧面单位面积平均摩擦力的估计项。通过引入了常数项使式(34)中的预设调整系数ksd取值接近于1，便于ksd值选择。显然，式(34)的第一项体现了粮堆侧面单位面积平均摩擦力对内外两圈压力传感器输出值均值的影响，第二项体现了对内外两圈压力传感器输出值标准差的影响。

实际建模结果表明，对于流动性较低的稻谷等粮堆，粮堆侧面压强相对较小，各圈标准差与粮堆重量的线性相关性高，宜采用式(34)所示的id(s)构造的估计。而针对稻谷等流动性较高的粮堆，可参考实施例1的式(15)来构建。

4.检测模型

对于式(30)所示的粮仓储粮数量理论检测模型，采用id(s)多项式构建和h的估计为：

其中，bb(m)、bh(j)、bf(n)分别为h和估计项的系数，m＝0,...,nb，j＝0,...,nh，n＝0,...,nf，nb、nh、nf分别为h和估计的多项式阶数。将式(35)至式(37)代入式(30)，则有：

整理式(30)，并限制项的最大阶数为nb，限制id(s)项的最大阶数为nf，可以得出：

其中，ab(m)、af(n,m)为估计项的系数，m＝0,...,nb，n＝1,...,nf，nb、nf分别为id(s)项的阶数。显然，式(39)的第一项总项数为nb+1，最大阶数为nb；第二项总项数为(nb+1)nf，与id(s)乘积项的最大阶数和为nb+nf。为了限制式(39)所示检测模型的非线性程度，应控制第二项中乘积项最大阶数和。因此，为了便于模型总项数优化，整理式(39)，对第二项按与id(s)乘积项的阶数和nn+m的升序排序，nn+m相同时按id(s)阶数由低到高排序，则有

其中，nn+m为检测模型第二项中与id(s)乘积项的阶数和，取值区间为[1,nb+nf]；mb、me取值如下二式所示：

显然，式(39)第二项的乘积项总数为(nb+1)nf，模型项总数nitem的最大值为nb+(nb+1)nf+1。为了限制式模型的非线性程度，可从模型尾部(第nb+(nb+1)nf+1乘积项)项开始，去除若干乘积项项，以减少模型项总数nitem。

式(40)为基于底面两圈压力传感器和id(s)的多项式粮仓储粮数量检测模型。根据id(s)项的特点，该模型适用于稻谷等流动性较低的粮食粮仓储粮数量检测。

5.建模方法

对于给定的样本集其中，k为样本点号，k＝1,2,3,...,m，m为样本个数；为第k个样本点的内圈压力传感器输出值序列，i＝1,2,...,ni，ni为内圈压力传感器个数；为第k个样本点的外圈压力传感器输出值序列，j＝1,2,...,no，no为外圈压力传感器个数；w^k为样本点k的实际进粮重量，为相应的粮仓底面面积。将样本集s分为三个部分，分别作为多元回归样本集sm、参数优化样本集so与测试样本集st。通过多元回归样本集sm样本与参数优化样本集so样本的不同，以避免模型过学习，提高模型的泛化能力。当样本数小时，将样本集s分为两个部分，一部分同时作为多元回归样本集sm和参数优化样本集so，另外一部分作为测试样本集st。

对于式(31)、式(34)和式(40)，任意选定一组id(s)多项式的最大阶数(nb,nf)，则可利用多元回归样本集sm和多元回归方法确定相应的ab(m)和af(n,m)。利用所建立的回归模型和参数优化样本集so，依据下式所示的百分比误差模型计算参数优化样本集so和多元回归样本集sm的预测误差e(nb,nf)：

其中，为样本点k的粮堆重量预测值。设定nb选择范围为[1，maxnb]，nf选择范围为[1，maxnf]，在本发明研究中，一般取maxnb和maxnf为4-10。若：

则为id(s)项最佳最大阶数。

6.检测实例与结果分析

6.1检测实例1

实验所采用的平房仓长9m，宽4.2m，面积为37.8m²，cb/ab＝0.698。粮仓均属于小型粮仓，cb/ab相对较大。根据图1所示的压力传感器布置模型，压力传感器分2圈布置，内圈6个，外圈16个，共22个压力传感器。稻谷粮堆高度约6米，进粮时每1米取一次数据，重复5次实验共获得30个样本。

对于式(40)所示的基于底面两圈压力传感器和id(s)的多项式粮仓储粮数量检测模型，将全部30个样本作为建模样本。优化后的建模参数如表10所示，获得的参数如表11和12所示。粮仓储粮重量计算误差如图11所示，最大百分比误差为1.58e-6％。

表10最佳最大阶数和

表11模型系数ab(m)

表12模型系数af(n,m)

表12(续)模型系数af(n,m)

对于式(40)所示的基于底面两圈压力传感器和id(s)的多项式粮仓储粮数量检测模型，以实验2的7至12号样本作为测试样本，利用实验3的13至18号样本作为参数优化样本集，其余18个样本作为建模样本。优化后的建模参数如表13所示，获得的参数如表14和15所示。粮仓储粮重量计算误差如图12所示，最大测试百分比误差为1.76％。由于建模样本过少，使得最大测试误差较大，如果增大建模样本数量，则可进一步减少预测误差。

表13最佳最大阶数和

表14模型系数ab(m)

表15模型系数af(n,m)

6.2检测实例2

对于通州粮库的4个稻谷粮仓和洪泽的2个稻谷粮仓，储粮重量分别为6450吨、4420吨、3215吨、64500吨、2455.6吨和2099.9吨。从长时间检测数据中选取样本1231个。选取922个作为多元回归样本集和参数优化样本集，其它作为测试样本集。对于式(40)所示的基于底面两圈压力传感器和id(s)的多项式粮仓储粮数量检测模型，优化后的建模参数如表16所示，获得的参数如表17和18所示。建模样本的粮仓储粮重量计算误差如图13所示，所有样本的粮仓储粮重量计算误差如图14所示。从这些结果中可以看出，建模样本和测试样本的粮仓储粮重量计算误差均小于0.087％。

表16最佳最大阶数和

表17模型系数ab(m)

表18模型系数af(n,m)

18(续)模型系数af(n,m)

本发明所提出的基于底面两圈压力传感器输出值标准差的粮仓储粮数量检测模型与粮仓重量检测方法也可按图10所示的实施方式实施，具体步骤实施如下：

(1)系统配置

选定具体压力传感器，并配置相应的数据采集、数据传输等系统。

(2)底面压力传感器安装

平房仓传感器布置如图1所示，筒仓如图2所示，底面压力传感器按外圈和内圈两圈布置，外圈压力传感器均与侧面墙距离为d＞0且d＜1米，内圈压力传感器均与侧面墙距离d＞2米。两圈压力传感器个数均为6-10，传感器间距应不小于1m。

(3)系统标定与模型建模

对于给定的传感器、粮食种类以及仓型，如果系统尚未有标定，则在多于6个粮仓中布置压力传感器，进粮至满仓，压力传感器输出值稳定后，采集各仓的压力传感器输出值，形成样本集其中，k为样本点号，k＝1,2,3,...,m，m为样本个数；为第k个样本点的内圈压力传感器输出值序列，i＝1,2,...,ni，ni为内圈压力传感器个数；为第k个样本点的外圈压力传感器输出值序列，j＝1,2,...,no，no为外圈压力传感器个数；w^k为样本点k的实际进粮重量，为相应的粮仓底面面积。将样本集s分为三个部分，分别作为多元回归样本集sm、参数优化样本集so与测试样本集st。根据多元回归样本集sm，利用回归方法确定式(40)中的回归参数ab(m)和af(n,m)，并根据所建立的回归模型和参数优化样本集so，利用式(43)、式(44)优化id(s)多项式的最大阶数nb和nf，从而构造出式(40)所示的粮仓储粮数量检测模型。

(4)实仓重量检测

如果系统已标定，检测底面压力传感器输出并利用式(40)所示模型进行粮仓储粮数量检测。