地震数据插值方法及系统与流程

本发明涉及地球物理勘探技术领域，更具体地，涉及一种地震数据插值方法及系统。

背景技术：

在地震勘探采集过程中，由于经济成本限制、检波器异常、坏道、地区开采限制等因素，往往导致地震数据出现缺失道或者偏移距不够大等问题，这对于地震资料处理的一些环节影响较大，特别是高分辨率处理、波动方程偏移、全波形反演等技术往往需要完整的规则数据。数据插值技术作为地震资料数据重构的重要手段，在这方面起着不可替代的作用。

随着地震勘探技术的不断发展，目前已经有多种插值方法，从方法上区分，目前主要分为三类：第一类是预测滤波器插值技术，这种方法主要是将数据傅里叶变换到频率域，设计预测滤波器算子进行数据重构。该类方法对于规则地震资料缺失具有较好的插值效果，但对于不规则的缺失数据而言，该方法多解性较强，效果不佳；第二类方法是基于波动方程的地震资料插值，通过地震资料道之间的因果相关性进行约束插值。该方法相对于预测滤波器类方法适应性更强，对于规则或者非规则的缺失数据插值均具有较好的效果，但由于该方法基于波动方程，因此对速度场的精度要求较高，错误的速度场往往产生较大的误差；第三类是基于多域变换的方法，目前大多数主流方法均属于该类，它通过将数据进行某种变换再利用各种算法进行数据插值，包括拉东变换、傅里叶变换、小波变换等方法。虽然这类方法不需要地质模型约束，且对于非规则缺失数据插值效果较好，但该类方法需要人为设定阈值，插值效果依赖于处理人员的经验，且该类方法往往耗费大量的人力及时间，因此该类方法也存在着一些不足。因此，有必要开发一种智能化的地震数据插值方法及系统。

公开于本发明背景技术部分的信息仅仅旨在加深对本发明的一般背景技术的理解，而不应当被视为承认或以任何形式暗示该信息构成已为本领域技术人员所公知的现有技术。

技术实现要素：

本发明提出了一种地震数据插值方法及系统，其能够通过采用有监督学习的深度学习方式，利用大量数据训练神经网络模型，通过自主机器学习完成缺失地震道的数据重构，避免人为干涉，提高地震预处理环节的效率，实现真正意义上的智能化插值技术。

根据本发明的一方面，提出了一种地震数据插值方法。所述方法可以包括：建立包括多个单炮记录的期望炮集，将所述期望炮集中的每个单炮记录随机删除部分地震道，获得初始炮集；设定初始第一权重、初始第二权重、初始第一数据扰动项、初始第二数据扰动项；根据所述初始第一权重、初始第一数据扰动项、所述初始炮集，进行卷积神经网络提取，将获得的结果作为所述初始炮集，重复进行卷积神经网络提取，将获得的结果作为压缩炮集；根据所述初始第二权重、初始第二数据扰动项、所述压缩炮集，进行全连接计算，获得全连接炮集，根据所述全连接炮集进行双线性内插，获得复原炮集；根据所述复原炮集与所述期望炮集，通过最小均方差函数，计算优化炮集，根据所述优化炮集，获得优化第一权重、优化第二权重、优化第一数据扰动项、优化第二数据扰动项，建立插值计算模型；将目标炮集代入所述插值计算模型，获得插值后的炮集。

优选地，根据所述复原炮集与所述期望炮集，通过最小均方差函数，计算优化炮集包括：步骤501：设定优化阈值；步骤502：通过最小均方差函数，计算所述复原炮集与所述期望炮集的均方差；步骤503：判断所述均方差是否小于所述优化阈值，若是，则以所述复原炮集为所述优化炮集，若否，则调节所述初始第一权重、所述初始第二权重、所述初始第一数据扰动项、所述初始第二数据扰动项，获得新的复原炮集，重复步骤502-503，直至所述均方差小于所述优化阈值。

优选地，通过公式(1)计算所述复原炮集与所述期望炮集的均方差：

其中，e表示均方差，uk表示复原炮集中的第k个单炮记录，yk表示期望炮集中的第k个单炮记录，n表示单炮记录总数。

优选地，通过公式(2)进行卷积神经网络提取：

其中，xi表示初始炮集中的第i个单炮记录，w表示第一权重的矩阵，wi表示第一权重矩阵的参量，b为第一数据扰动项，n表示单炮记录总数，f表示激活函数，其中，激活函数为：

其中，z为激活函数的参量。

优选地，通过公式(4)进行全连接计算：

其中，a＝(a1,a2,…,am)表示全连接炮集，表示第二权重的矩阵，表示第二数据扰动项的矩阵，表示压缩炮集的矩阵。

根据本发明的另一方面，提出了一种地震数据插值系统，其特征在于，该系统包括：存储器，存储有计算机可执行指令；处理器，所述处理器运行所述存储器中的计算机可执行指令，执行以下步骤：建立包括多个单炮记录的期望炮集，将所述期望炮集中的每个单炮记录随机删除部分地震道，获得初始炮集；设定初始第一权重、初始第二权重、初始第一数据扰动项、初始第二数据扰动项；根据所述初始第一权重、初始第一数据扰动项、所述初始炮集，进行卷积神经网络提取，将获得的结果作为所述初始炮集，重复进行卷积神经网络提取，将获得的结果作为压缩炮集；根据所述初始第二权重、初始第二数据扰动项、所述压缩炮集，进行全连接计算，获得全连接炮集，根据所述全连接炮集进行双线性内插，获得复原炮集；根据所述复原炮集与所述期望炮集，通过最小均方差函数，计算优化炮集，根据所述优化炮集，获得优化第一权重、优化第二权重、优化第一数据扰动项、优化第二数据扰动项，建立插值计算模型；将目标炮集代入所述插值计算模型，获得插值后的炮集。

优选地，根据所述复原炮集与所述期望炮集，通过最小均方差函数，计算优化炮集包括：步骤501：设定优化阈值；步骤502：通过最小均方差函数，计算所述复原炮集与所述期望炮集的均方差；步骤503：判断所述均方差是否小于所述优化阈值，若是，则以所述复原炮集为所述优化炮集，若否，则调节所述初始第一权重、所述初始第二权重、所述初始第一数据扰动项、所述初始第二数据扰动项，获得新的复原炮集，重复步骤502-503，直至所述均方差小于所述优化阈值。

优选地，通过公式(1)计算所述复原炮集与所述期望炮集的均方差：

其中，e表示均方差，uk表示复原炮集中的第k个单炮记录，yk表示期望炮集中的第k个单炮记录，n表示单炮记录总数。

优选地，通过公式(2)进行卷积神经网络提取：

其中，xi表示初始炮集中的第i个单炮记录，w表示第一权重的矩阵，wi表示第一权重矩阵的参量，b为第一数据扰动项，n表示单炮记录总数，f表示激活函数，其中，激活函数为：

其中，z为激活函数的参量。

优选地，通过公式(4)进行全连接计算：

其中，a＝(a1,a2,…,am)表示全连接炮集，表示第二权重的矩阵，表示第二数据扰动项的矩阵，表示压缩炮集的矩阵。

其有益效果在于：利用卷积神经网络技术提取地震数据的特征信息，开展面向地震勘探的数据挖掘算法研究，建立基于二维卷积算法及全连接算法的深度神经网络框架，采用有监督学习的方式，利用大量数据训练神经网络模型，通过自主机器学习完成缺失地震道的数据重构，避免人为干涉，提高地震预处理环节的效率，实现真正意义上的智能化插值技术。

(1)利用卷积神经网络算法，挖掘地震资料特征信息的同时实现数据的低秩降维；

(2)利用全连接层技术增强了模型的表达能力，使模型能够适用于复杂构造的精确插值；

(3)将双线性内插算法引入模型中，用于数据尺寸的恢复，实现数据对数据的模型映射关系；

(4)更新模型方面，采用随机梯度下降技术进行模型的进化更新。

本发明具有其它的特性和优点，这些特性和优点从并入本文中的附图和随后的具体实施方式中将是显而易见的，或者将在并入本文中的附图和随后的具体实施方式中进行详细陈述，这些附图和具体实施方式共同用于解释本发明的特定原理。

附图说明

通过结合附图对本发明示例性实施例进行更详细的描述，本发明的上述以及其它目的、特征和优势将变得更加明显，其中，在本发明示例性实施例中，相同的参考标号通常代表相同部件。

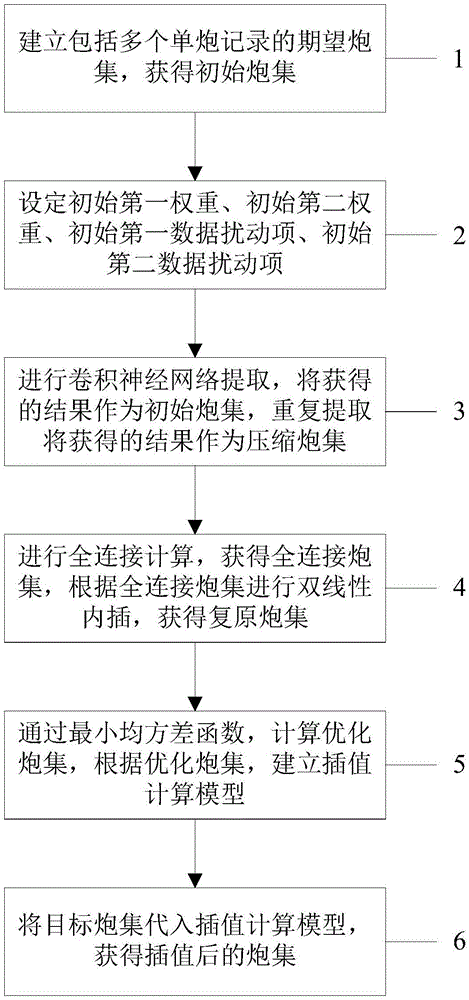
图1示出了根据本发明的地震数据插值方法的步骤的流程图。

图2示出了根据本发明的一个实施例的地震单炮记录的示意图。

图3示出了根据本发明的一个实施例的随机剔除25％地震道的单炮记录的示意图。

图4示出了根据本发明的一个实施例的复原炮集的示意图。

图5示出了根据本发明的一个实施例的复原炮集与期望炮集的均方差的示意图，横坐标为迭代次数，纵坐标为均方差(％)。

图6示出了根据本发明的一个实施例的原始缺失数据与插值的重构数据的对比图，其中横坐标表示时间(s)，纵坐标表示振幅。

图7a、7b、7c分别示出了根据本发明的一个实施例的浅层强信号原始数据、缺失数据及插值后数据的对比图。

图8a、8b、8c分别示出了根据本发明的一个实施例的深层中强信号原始数据、缺失数据及插值后数据的对比图。

图9a、9b、9c分别示出了根据本发明的一个实施例的深层弱信号原始数据、缺失数据及插值后数据的对比图。

具体实施方式

下面将参照附图更详细地描述本发明。虽然附图中显示了本发明的优选实施例，然而应该理解，可以以各种形式实现本发明而不应被这里阐述的实施例所限制。相反，提供这些实施例是为了使本发明更加透彻和完整，并且能够将本发明的范围完整地传达给本领域的技术人员。

图1示出了根据本发明的地震数据插值方法的步骤的流程图。

在该实施例中，根据本发明的地震数据插值方法可以包括：步骤1，建立包括多个单炮记录的期望炮集，将期望炮集中的每个单炮记录随机删除部分地震道，获得初始炮集；步骤2，设定初始第一权重、初始第二权重、初始第一数据扰动项、初始第二数据扰动项；步骤3，根据初始第一权重、初始第一数据扰动项、初始炮集，进行卷积神经网络提取，将获得的结果作为初始炮集，重复进行卷积神经网络提取，将获得的结果作为压缩炮集；步骤4，根据初始第二权重、初始第二数据扰动项、压缩炮集，进行全连接计算，获得全连接炮集，根据全连接炮集进行双线性内插，获得复原炮集；步骤5，根据复原炮集与期望炮集，通过最小均方差函数，计算优化炮集，根据优化炮集，获得优化第一权重、优化第二权重、优化第一数据扰动项、优化第二数据扰动项，建立插值计算模型；步骤6，将目标炮集代入插值计算模型，获得插值后的炮集。

在一个示例中，根据复原炮集与期望炮集，通过最小均方差函数，计算优化炮集包括：步骤501：设定优化阈值；步骤502：通过最小均方差函数，计算复原炮集与期望炮集的均方差；步骤503：判断均方差是否小于优化阈值，若是，则以复原炮集为优化炮集，若否，则调节初始第一权重、初始第二权重、初始第一数据扰动项、初始第二数据扰动项，获得新的复原炮集，重复步骤502-503，直至均方差小于优化阈值。

在一个示例中，通过公式(1)计算复原炮集与期望炮集的均方差：

其中，e表示均方差，uk表示复原炮集中的第k个单炮记录，yk表示期望炮集中的第k个单炮记录，n表示单炮记录总数。

在一个示例中，通过公式(2)进行卷积神经网络提取：

其中，xi表示初始炮集中的第i个单炮记录，w表示第一权重的矩阵，wi表示第一权重矩阵的参量，b为第一数据扰动项，n表示单炮记录总数，f表示激活函数，其中，激活函数为：

其中，z为激活函数的参量。

在一个示例中，通过公式(4)进行全连接计算：

其中，a＝(a1,a2,…,am)表示全连接炮集，表示第二权重的矩阵，表示第二数据扰动项的矩阵，表示压缩炮集的矩阵。

具体地，根据本发明的地震数据插值方法可以包括：步骤1，建立包括多个单炮记录的期望炮集，将期望炮集中的每个单炮记录随机删除部分地震道，获得初始炮集；步骤2，设定初始第一权重、初始第二权重、初始第一数据扰动项、初始第二数据扰动项；步骤3，根据初始第一权重、初始第一数据扰动项、初始炮集，通过公式(2)进行卷积神经网络提取，其中，激活函数为公式(3)，将获得的结果作为初始炮集，重复进行卷积神经网络提取，将获得的结果作为压缩炮集；步骤4，根据初始第二权重、初始第二数据扰动项、压缩炮集，通过公式(4)进行全连接计算，获得全连接炮集，根据全连接炮集进行双线性内插，获得复原炮集；步骤5，根据复原炮集与期望炮集，通过最小均方差函数，计算优化炮集，根据优化炮集，获得优化第一权重、优化第二权重、优化第一数据扰动项、优化第二数据扰动项，建立插值计算模型，其中，计算优化炮集包括：步骤501：设定优化阈值；步骤502：通过最小均方差函数，通过公式(1)计算复原炮集与期望炮集的均方差；步骤503：判断均方差是否小于优化阈值，若是，则以复原炮集为优化炮集，若否，则调节初始第一权重、初始第二权重、初始第一数据扰动项、初始第二数据扰动项，计算新的复原炮集，重复步骤502-503，直至均方差小于优化阈值；步骤6，将目标炮集代入插值计算模型，获得插值后的炮集。

本方法通过有监督学习的深度学习方式，利用大量数据训练神经网络模型，通过自主机器学习完成缺失地震道的数据重构，避免人为干涉，提高地震预处理环节的效率，实现真正意义上的智能化插值技术。

应用示例

为便于理解本发明实施例的方案及其效果，以下给出一个具体应用示例。本领域技术人员应理解，该示例仅为了便于理解本发明，其任何具体细节并非意在以任何方式限制本发明。

图2示出了根据本发明的一个实施例的地震单炮记录的示意图。

如图2所示，这是随机生成20000个单炮记录之一。激发方式采用中间放炮，两边接收的观测系统，左右两边各放置64个检波器，共128道接收，偏移距为50m，纵向采样点为1000，采样间隔为4ms。其中炮集对应的地层数、层速度、构造特征均为随机产生，以保证样本的随机性。

图3示出了根据本发明的一个实施例的随机剔除25％地震道的单炮记录的示意图。

如图3所示，对生成的每个单炮记录随机剔除25％的地震道用于模拟缺失地震数据，这是对应于图2生成的缺失道地震炮集。

图4示出了根据本发明的一个实施例的复原炮集的示意图。

如图4所示，这是利用神经网络模型计算得到的插值后的复原炮集，从结果中可以看出，该复原炮集插值效果整体较好，数据均得到较好的重构。

图5示出了根据本发明的一个实施例的复原炮集与期望炮集的均方差的示意图，横坐标为迭代次数，纵坐标为均方差(％)。

如图5所示，利用20000个样本组成数据训练集对模型进行迭代训练更新，该图是训练对应的收敛曲线，可以看出，该模型收敛迅速。

图6示出了根据本发明的一个实施例的原始缺失数据与插值的重构数据的对比图，其中横坐标表示时间(s)，纵坐标表示振幅。

如图6所示，提取出插值后的数据与期望值(原始缺失数据)进行对比，验证其准确度，通过单道对比可以更明显的看出，该模型具有较好的插值效果。其中纵坐标表示振幅，横坐标表示时间(s)。

图7a、7b、7c分别示出了根据本发明的一个实施例的浅层强信号原始数据、缺失数据及插值后数据的对比图。通过对插值前后的数据进行局部放大，验证浅层强信号的插值效果，通过对浅层强信号的局部方法，通过细节的对比验证该方法的插值效果。

图8a、8b、8c分别示出了根据本发明的一个实施例的深层中强信号原始数据、缺失数据及插值后数据的对比图。通过对插值前后的数据进行局部放大，验证深层中强信号的插值效果，通过对深层中强信号的局部方法，通过细节的对比验证该方法的插值效果。

图9a、9b、9c分别示出了根据本发明的一个实施例的深层弱信号原始数据、缺失数据及插值后数据的对比图。通过对插值前后的数据进行局部放大，验证深层弱信号的插值效果，通过对深层弱信号的局部方法，通过细节的对比验证该方法的插值效果。

综上所述，本发明通过有监督学习的深度学习方式，利用大量数据训练神经网络模型，通过自主机器学习完成缺失地震道的数据重构，避免人为干涉，提高地震预处理环节的效率，实现真正意义上的智能化插值技术。

本领域技术人员应理解，上面对本发明的实施例的描述的目的仅为了示例性地说明本发明的实施例的有益效果，并不意在将本发明的实施例限制于所给出的任何示例。

根据本发明的地震数据插值系统，其特征在于，该系统包括：存储器，存储有计算机可执行指令；处理器，处理器运行存储器中的计算机可执行指令，执行以下步骤：建立包括多个单炮记录的期望炮集，将期望炮集中的每个单炮记录随机删除部分地震道，获得初始炮集；设定初始第一权重、初始第二权重、初始第一数据扰动项、初始第二数据扰动项；根据初始第一权重、初始第一数据扰动项、初始炮集，进行卷积神经网络提取，将获得的结果作为初始炮集，重复进行卷积神经网络提取，将获得的结果作为压缩炮集；根据初始第二权重、初始第二数据扰动项、压缩炮集，进行全连接计算，获得全连接炮集，根据全连接炮集进行双线性内插，获得复原炮集；根据复原炮集与期望炮集，通过最小均方差函数，计算优化炮集，根据优化炮集，获得优化第一权重、优化第二权重、优化第一数据扰动项、优化第二数据扰动项，建立插值计算模型；将目标炮集代入插值计算模型，获得插值后的炮集。

在一个示例中，根据复原炮集与期望炮集，通过最小均方差函数，计算优化炮集包括：步骤501：设定优化阈值；步骤502：通过最小均方差函数，计算复原炮集与期望炮集的均方差；步骤503：判断均方差是否小于优化阈值，若是，则以复原炮集为优化炮集，若否，则调节初始第一权重、初始第二权重、初始第一数据扰动项、初始第二数据扰动项，获得新的复原炮集，重复步骤502-503，直至均方差小于优化阈值。

在一个示例中，通过公式(1)计算复原炮集与期望炮集的均方差：

其中，e表示均方差，uk表示复原炮集中的第k个单炮记录，yk表示期望炮集中的第k个单炮记录，n表示单炮记录总数。

在一个示例中，通过公式(2)进行卷积神经网络提取：

其中，xi表示初始炮集中的第i个单炮记录，w表示第一权重的矩阵，wi表示第一权重矩阵的参量，b为第一数据扰动项，n表示单炮记录总数，f表示激活函数，其中，激活函数为：

其中，z为激活函数的参量。

在一个示例中，通过公式(4)进行全连接计算：

其中，a＝(a1,a2,…,am)表示全连接炮集，表示第二权重的矩阵，表示第二数据扰动项的矩阵，表示压缩炮集的矩阵。

本系统通过有监督学习的深度学习方式，利用大量数据训练神经网络模型，通过自主机器学习完成缺失地震道的数据重构，避免人为干涉，提高地震预处理环节的效率，实现真正意义上的智能化插值技术。

以上已经描述了本发明的各实施例，上述说明是示例性的，并非穷尽性的，并且也不限于所披露的各实施例。在不偏离所说明的各实施例的范围和精神的情况下，对于本技术领域的普通技术人员来说许多修改和变更都是显而易见的。