一种用于地震道编辑的数据预处理方法及系统与流程

本发明涉及石油地震勘探数据处理技术领域，尤其涉及一种用于地震道编辑的数据预处理方法及系统。

背景技术：

数据预处理在众多算法中都起着重要作用，现有的机器学习算法可以应用在地震道编辑算法中，但前提是需要对数据进行预处理。现有的常规数据预处理中的算法过于简单粗暴，对地震数据预处理的效果并不十分好。且上述预处理的方法并没有针对地震道编辑有一个较为常用的使用流程，方便地震数据处理人员进行数据处理。

因此，如何对地震数据进行处理，针对地震道编辑一个较为常用的使用流程便地震数据处理人员进行数据处理是本领域亟待解决的问题。

技术实现要素：

本发明的特征和优点在下文的描述中部分地陈述，或者可从该描述显而易见，或者可通过实践本发明而学习。

为克服现有技术的问题，本发明提供一种用于地震道编辑的数据预处理方法，包括步骤：

s1、将地震数据进行异常值剔除；

s2、将异常值剔除后的地震数据进行数据归一化；

s3、将数据归一化后的地震数据进行zca白化。

可选地，所述步骤s1包括：

对n维的数据集合计算每个维度的均值和方差μj，σj，j∈{1,...n}；

对新的数据计算概率值若所述概率值小于预设阈值，则判定新的数据属于异常值，其中：

可选地，所述步骤s2中采用特征标准化来对地震数据进行归一化。

可选地，所述步骤s3包括：

s31、计算数据集的协方差矩阵∑；

s32、对所述协方差矩阵∑进行svd分解，得到u向量u^tx，并利用u^tx，得到数据集经过旋转后的结果xrot；

s33、将xrot中的每一维都除以得到xpcawhite,i，其中是xrot协方差矩阵对角元素的值；

s34、将xpcawhite,i左乘一个特征向量矩阵u，得到zca白化。

可选地，在所述步骤s3中保留数据的维度不变。

本发明还提供一种用于地震道编辑的数据预处理系统，包括：

异常值剔除单元，用于将地震数据进行异常值剔除；

归一化单元，与所述异常值剔除单元相连，用于将异常值剔除后的地震数据进行数据归一化；

zca白化单元，与所述归一化单元相连，用于将数据归一化后的地震数据进行zca白化。

可选地，所述异常值剔除单元用于：

对n维的数据集合计算每个维度的均值和方差μj，σj，j∈{1,...n}；

对新的数据计算概率值若所述概率值小于预设阈值，则判定新的数据属于异常值，其中：

可选地，所述归一化单元用于采用特征标准化来对地震数据进行归一化。

可选地，所述zca白化单元用于：

计算数据集的协方差矩阵∑；

对所述协方差矩阵∑进行svd分解，得到u向量u^tx，并利用u^tx，得到数据集经过旋转后的结果xrot；

将xrot中的每一维都除以得到xpcawhite,i，其中是xrot协方差矩阵对角元素的值；

将xpcawhite,i左乘一个特征向量矩阵u，得到zca白化。

本发明提供一种计算机可读存储介质，所述计算机可读存储介质存储有计算机可执行的至少一个程序，其特征在于，所述至少一个程序被所述计算机执行时使所述计算机执行本发明任一实施例提供的用于地震道编辑的数据预处理方法中的步骤。

本发明提供了一种用于地震道编辑的数据预处理方法及其系统，为用于地震道编辑属性提取之后数据预处理提供一种较为常用的处理流程，为处理解释人员提供方便。

通过阅读说明书，本领域普通技术人员将更好地了解这些技术方案的特征和内容。

附图说明

下面通过参考附图并结合实例具体地描述本发明，本发明的优点和实现方式将会更加明显，其中附图所示内容仅用于对本发明的解释说明，而不构成对本发明的任何意义上的限制，在附图中：

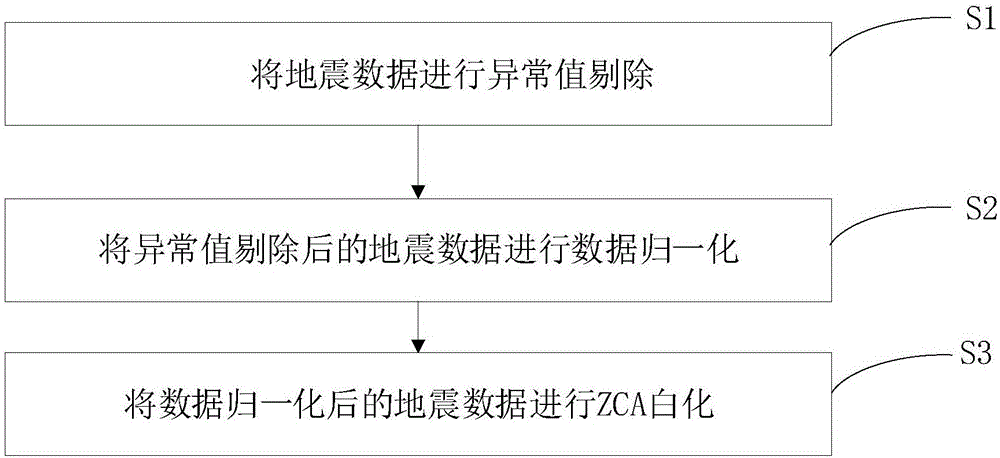
图1为本发明实施例的数据预处理方法的流程示意图。

图2为本发明实施例的数据预处理系统的结构示意图。

图3为未进行数据预处理得到的地震道编辑结果的示意图。

图4为进行数据预处理后得到的地震道编辑结果的示意图。

图5为未进行数据预处理得到的地震道编辑结果的示意图。

图6为进行数据预处理后得到的地震道编辑结果的示意图。

具体实施方式

如图1所示，本发明提供一种用于地震道编辑的数据预处理方法，包括步骤：

s1、将地震数据进行异常值剔除。

异常值是找出其数值不同于预期对象的检测过程。这些对象被称为异常点或者离群点。进行异常点检测的方法有很多，本发明采用基于统计学的方法。假设n维的数据集合形如那么可以计算每个维度的均值和方差μj，σj，j∈{1,...n}，具体来说，对于j∈{1,...n}，可以计算

在正态分布的假设下，如果有一个新的数据可以计算概率如下：

根据概率值的大小就可以判断x是否属于异常值；若所述概率值小于预设阈值，一般地，预设阈值为3％～8％；例如是3％、5％。则判定新的数据属于异常值。

s2、将异常值剔除后的地震数据进行数据归一化。

数据归一化常用的方法可以采取例如简单缩放、逐样本均值消减、特征标准化等。本实施例中选用特征标准化来对地震数据进行归一化。特征标准化指的是(独立地)使得数据的每一个维度具有零均值和单位方差。这是归一化中最常见的方法并被广泛地使用。应用到本实施例中，特征标准化的具体做法是：首先计算每一个地震属性上数据的均值(使用全体数据计算)，之后在每一个地震属性上都减去该均值，下一步便是在数据的每一地震属性上除以该地震属性数据的标准差。

s3、将数据归一化后的地震数据进行zca白化。

zca白化的主要用于去相关性，尽量使白化后的数据接近原始输入数据。对于含有m个样本的数据集{x⁽¹⁾,x⁽²⁾,...x^(m)}，假设每个样本的维度为n，即对其进行zca白化的具体步骤如下：

s31、计算数据集的协方差矩阵∑，计算公式如下：

s32、对所述协方差矩阵∑进行svd分解，得到u向量u^tx，并利用u^tx，得到数据集经过旋转后的结果xrot，即：

s33、将xrot中的每一维都除以得到xpcawhite,i，使输入特征具有单位方差，其中是xrot协方差矩阵对角元素的值，计算公式如下：

s34、将xpcawhite,i左乘一个特征向量矩阵u，得到我们需要的zca白化，其计算公式如下：

xzcawhite＝uxpcawhite(7)

需要注意的是，在使用zca白化这个过程中即步骤s3中，需要保留数据的全部n个维度，即维持数据的维度不变，不对数据进行降维。

本发明还提供一种计算机可读存储介质，所述计算机可读存储介质存储有计算机可执行的至少一个程序，所述至少一个程序被所述计算机执行时使所述计算机执行本发明任一实施例提供的用于地震道编辑的数据预处理方法中的步骤。

如图2所示，本发明提供一种用于地震道编辑的数据预处理系统，包括异常值剔除单元10、归一化单元20以及zca白化单元30。其中：

异常值剔除单元10用于将地震数据进行异常值剔除。更具体地，假设n维的数据集合形如那么可以计算每个维度的均值和方差μj，σj，j∈{1,...n}，具体来说，对于j∈{1,...n}，可以计算

在正态分布的假设下，如果有一个新的数据可以计算概率如下：

根据概率值的大小就可以判断x是否属于异常值；若所述概率值小于预设阈值，一般地，预设阈值为3％～8％；例如是3％、5％。则判定新的数据属于异常值。

归一化单元20与所述异常值剔除单元10相连，用于将异常值剔除后的地震数据进行数据归一化。本实施例中，采用特征标准化来对地震数据进行归一化。特征标准化的具体做法是：首先计算每一个地震属性上数据的均值(使用全体数据计算)，之后在每一个地震属性上都减去该均值，下一步便是在数据的每一地震属性上除以该地震属性数据的标准差。

zca白化单元30与所述归一化单元20相连，用于将数据归一化后的地震数据进行zca白化。

更具体地，所述zca白化单元用于：计算数据集的协方差矩阵∑；对所述协方差矩阵∑进行svd分解，得到u向量u^tx，并利用u^tx，得到数据集经过旋转后的结果xrot；将xrot中的每一维都除以得到xpcawhite,i，其中是xrot协方差矩阵对角元素的值；将xpcawhite,i左乘一个特征向量矩阵u，得到zca白化。其采用的具体公式与上述步骤s31至s34一致，在此不再赘述。

下面辅以实际地震道编辑实例进一步说明，首先对地震数据进行预处理，再进行道编辑计算。第一组数据在未进行数据预处理时得到的地震道编辑结果如图3所示；采用本发明提供的用于地震道编辑的数据预处理方法、系统或计算机可读存储介质对第一组数据进行数据预处理后得到的地震道编辑结果如图4所示。第二组数据在未进行数据预处理时得到的地震道编辑结果如图5所示；采用本发明提供的用于地震道编辑的数据预处理方法、系统或计算机可读存储介质对第二组数据进行数据预处理后得到的地震道编辑结果如图6所示可见，本发明能有效提高结果精度。

本发明提供的用于地震道编辑的数据预处理方法及其系统、计算机可读存储介质，先通过地震数据异常值剔除，再对地震数据进行特征标准化，最后对数据进行zca白化。本发明原理简单，实现方便，计算速度快，能有效提高地震数据道编辑的准确率，经过资料测试验证，可以显著有效提高地震道编辑的效果，也有效地验证了方法的可靠性。

以上参照附图说明了本发明的优选实施例，本领域技术人员不脱离本发明的范围和实质，可以有多种变型方案实现本发明。举例而言，作为一个实施例的部分示出或描述的特征可用于另一实施例以得到又一实施例。以上仅为本发明较佳可行的实施例而已，并非因此局限本发明的权利范围，凡运用本发明说明书及附图内容所作的等效变化，均包含于本发明的权利范围之内。