一种多尺度近地表层析速度建模方法及建模系统与流程

本发明属于油气勘探领域，具体涉及一种多尺度近地表层析速度建模方法及建模系统。

背景技术：

随着地震勘探向双复杂地区推进，地表高程与近地表速度、厚度变化剧烈，给地震高精度成像带来了巨大挑战。为了提高地下构造成像精度，建立更精细的近地表速度模型是关键技术之一。近地表初至波走时层析速度建模是当前近地表建模常用方法。该方法通过拾取初至波走时，根据初始模型理论走时与拾取走时残差求取模型修改量，对速度模型不断更新迭代，逐步缩小理论走时与观测走时误差，得到最终的速度模型。该方法基于稳健且易识别的初至波走时信息，最终形成一个平滑的近地表模型，为后续计算静校正及速度融合提供速度模型。

匹配走时残差获得模型修改量是该方法的核心。目前主要的方法有三大类：第一类是通过建立层析方程组，通过数学工具进行求解，这类方法的典型代表是lsqr法。这类方法求解灵活，但是由于射线层析矩阵病态性强，矩阵求解不稳定，影响反演精度；第二类是通过反投影的方法将走时残差平均在射线路径上，这类方法的典型代表是sirt法。这类方法反演结果稳定，缺点是分辨率低；第三类方法是伴随状态法，该方法不需要进行射线追踪，通过两次正演的计算量就可以获得速度修改量。该方法省去了传统射线追踪的过程，但是物理意义不明确，且hessian矩阵建立较困难，提高精度的能力有限。因此，对此特别需要一种合理的近地表速度模型方法，能提高反演效率，提高反演精度。

技术实现要素：

本发明的目的是提出一种提高反演效率和反演精度的多尺度近地表层析速度建模方法及建模系统。

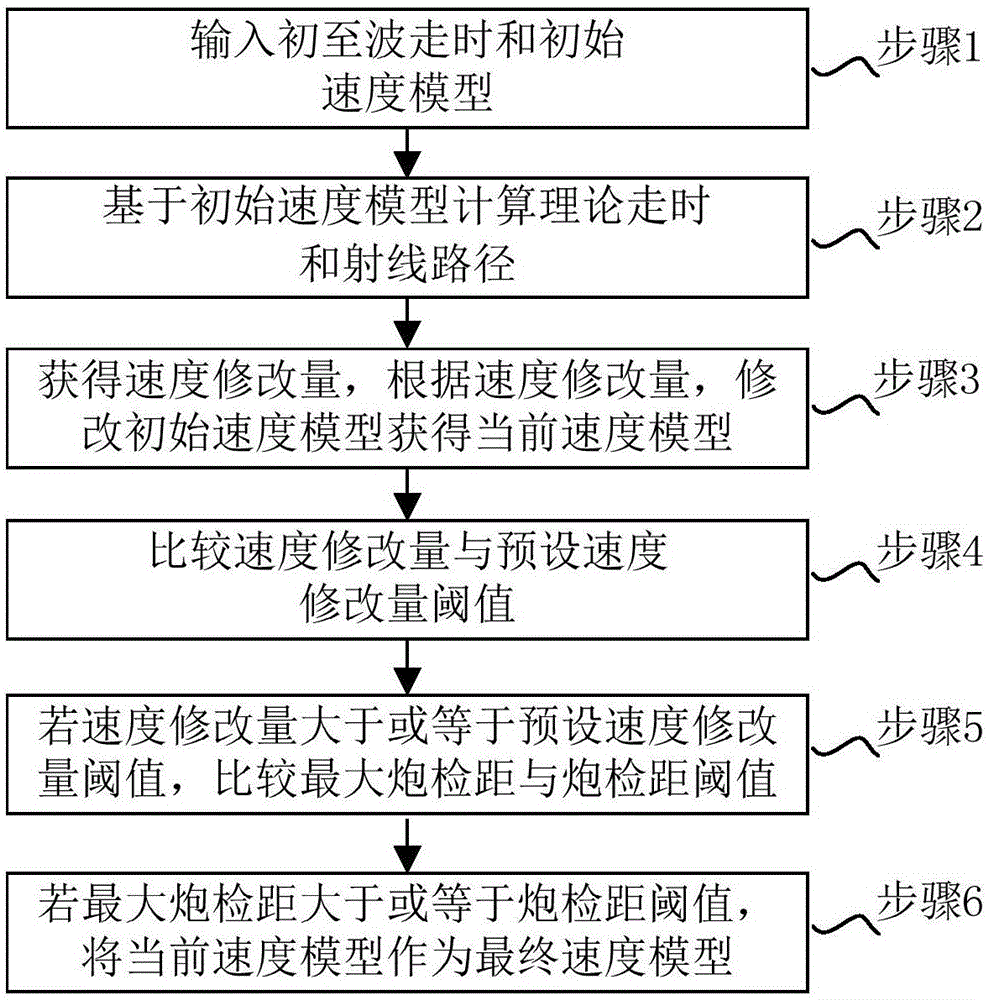
为了实现上述目的，本发明提供一种多尺度近地表层析速度建模方法，包括：步骤1：输入初至波走时和初始速度模型；步骤2：基于所述初始速度模型计算理论走时和射线路径；步骤3：获得速度修改量，根据所述速度修改量，修改所述初始速度模型获得当前速度模型；步骤4：比较所述速度修改量与预设速度修改量阈值；步骤5：若所述速度修改量大于或等于预设速度修改量阈值，则比较最大炮检距与炮检距阈值；步骤6：若所述最大炮检距大于或等于所述炮检距阈值，则将当前速度模型作为最终速度模型。

优选的，所述多尺度近地表层析速度建模方法，还包括：若所述速度修改量小于所述预设速度修改量阈值，则返回步骤2并将当前速度模型作为所述初始速度模型。

优选的，所述多尺度近地表层析速度建模方法，还包括：若所述最大炮检距小于所述炮检距阈值，则返回步骤1，并减小所述最大炮检距，将当前速度模型作为所述初始速度模型。

优选的，通过射线追踪法计算所述理论走时和射线路径。

优选的，通过改进散射积分算法获得所述速度修改量。

优选的，所述通过改进散射积分算法获得所述速度修改量，包括：存储单一炮检对的射线路径，计算梯度；根据所述梯度，获取所述速度修改量。

优选的，通过模型迭代方法获得当前速度模型，所述模型迭代方法使用的公式为：

ml+1＝ml+αlpl(1)

其中，ml+1为当前速度模型，ml为初始速度模型，下标l为迭代进行到了第l轮，αlpl为速度修改量，pl为梯度，αl为固定步长。

本发明提供还提供一种多尺度近地表层析速度建模系统，该系统包括：存储器，存储有计算机可执行指令；处理器，所述处理器运行所述存储器中的计算机可执行指令，执行以下步骤：步骤1：输入初至波走时和初始速度模型；步骤2：基于所述初始速度模型计算理论走时和射线路径；步骤3：获得速度修改量，根据所述速度修改量，修改所述初始速度模型获得当前速度模型；步骤4：比较所述速度修改量与预设速度修改量阈值；步骤5：若所述速度修改量大于或等于预设速度修改量阈值，则比较最大炮检距与炮检距阈值；步骤6：若所述最大炮检距大于或等于所述炮检距阈值，则将当前速度模型作为最终速度模型。

优选的，所述多尺度近地表层析速度建模系统，还包括：若所述速度修改量小于所述预设速度修改量阈值，则返回步骤2并将当前速度模型作为所述初始速度模型。

优选的，所述多尺度近地表层析速度建模系统，还包括：若所述最大炮检距小于所述炮检距阈值则返回步骤1，并减小所述最大炮检距，将当前速度模型作为所述初始速度模型。

本发明的有益效果在于：本发明的多尺度近地表层析速度建模方法通过输入初至波走时和初始速度模型，计算理论走时和射线路径，获得速度修改量，根据速度修改量修改初始速度模型以获取当前速度模型，并比较速度修改量与预设速度修改量阈值，若速度修改量大于或等于预设速度修改量阈值，则比较最大炮检距与炮检距阈值，若最大炮检距大于或等于炮检距阈值，则将当前速度模型作为最终速度模型，通过输入初至波走时和初始速度模型，以及根据速度修改量修改初始速度模型，提高了反演精度，可建立高精度近地表速度模型。

本发明的多尺度近地表层析速度建模方法通过若最大炮检距小于炮检距阈值，则减少最大炮检距，并将当前速度模型作为初始速度模型，重新输入初至波走时，进行初始速度模型的修改，从而采用了多尺度反演策略，提高了反演精度，可建立高精度近地表速度模型。

本发明的多尺度近地表层析速度建模方法通过改进散射积分算法获得速度修改量，该方法计算速度快、内存占用小，提高了反演效率，可进行大规模三维近地表速度建模。

本发明具有其它的特性和优点，这些特性和优点从并入本文中的附图和随后的具体实施例中将是显而易见的，或者将在并入本文中的附图和随后的具体实施例中进行详细陈述，这些附图和具体实施例共同用于解释本发明的特定原理。

附图说明

通过结合附图对本发明示例性实施方式进行更详细的描述，本发明的上述以及其它目的、特征和优势将变得更加明显，其中，在本发明示例性实施方式中，相同的参考标号通常代表相同部件。

图1示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的流程图。

图2示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的真实速度模型。

图3示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的初始速度模型。

图4示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的全数据层析速度模型。

图5示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的多尺度层析速度模型。

图6a示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的地下50m深度的反演结果。

图6b示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的地下100m深度的反演结果。

图6c示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的地下150m深度的反演结果。

图7a示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的横向距离5km的反演结果。

图7b示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的横向距离7km的反演结果。

图7c示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的横向距离9km的反演结果。

具体实施方式

下面将更详细地描述本发明的优选实施方式。虽然以下描述了本发明的优选实施方式，然而应该理解，可以以各种形式实现本发明而不应被这里阐述的实施方式所限制。相反，提供这些实施方式是为了使本发明更加透彻和完整，并且能够将本发明的范围完整地传达给本领域的技术人员。

根据本发明的多尺度近地表层析速度建模方法，包括：步骤1：输入初至波走时和初始速度模型；步骤2：基于初始速度模型计算理论走时和射线路径；步骤3：获得速度修改量，根据速度修改量，修改初始速度模型获得当前速度模型；步骤4：比较速度修改量与预设速度修改量阈值；步骤5：若速度修改量大于或等于预设速度修改量阈值，则比较最大炮检距与炮检距阈值；步骤6：若最大炮检距大于或等于炮检距阈值，则将当前速度模型作为最终速度模型。

具体地，获取观测系统的最大炮检距，输入最大炮检距范围内的初至波走时，以及输入初始速度模型，基于初始速度模型计算理论走时和射线路径，获得速度修改量，根据速度修改量修改初始速度模型以获取当前速度模型，并比较速度修改量与预设速度修改量阈值，若速度修改量大于或等于预设速度修改量阈值，则比较最大炮检距与炮检距阈值，若最大炮检距大于或等于炮检距阈值，则将当前速度模型作为最终速度模型。

根据示例性的实施方式多尺度近地表层析速度建模方法通过输入初至波走时和初始速度模型，以及根据速度修改量修改初始速度模型，提高了反演精度，可建立高精度近地表速度模型。

作为优选方案，多尺度近地表层析速度建模方法，还包括：若速度修改量小于预设速度修改量阈值，则返回步骤2并将当前速度模型作为初始速度模型。

具体的，根据速度修改量与预设速度修改量阈值的比较结果，若速度修改量小于预设速度修改量阈值，返回步骤2，并将前速度模型作为初始速度模型，重新获取速度修改量，以及修改初始速度模型。

作为优选方案，多尺度近地表层析速度建模方法，还包括：若最大炮检距小于炮检距阈值，则返回步骤1，并减小最大炮检距，将当前速度模型作为初始速度模型。

具体的，根据最大炮检距与炮检距阈值的比较结果，若最大炮检距小于炮检距阈值，则返回步骤1，并减小最大炮检距，将当前速度模型作为初始速度模型，输入最大炮检距范围内的初至波走时，重新获取速度修改量，修改速度模型。

根据示例性的实施方式多尺度近地表层析速度建模方法通过若最大炮检距小于炮检距阈值，则减少最大炮检距，将当前速度模型作为初始速度模型，重新输入初至波走时，进行初始速度模型的修改，从而采用了多尺度反演策略，提高了反演精度，可建立高精度近地表速度模型。

作为优选方案，通过射线追踪法计算理论走时和射线路径。

作为优选方案，通过改进散射积分算法获得速度修改量。

根据示例性的实施方式多尺度近地表层析速度建模方法通过改进散射积分算法获得速度修改量，该方法计算速度快、内存占用小，提高了反演效率，可进行大规模三维近地表速度建模。

作为优选方案，通过改进散射积分算法获得速度修改量，包括：存储单一炮检对的射线路径，计算梯度；根据梯度，获取速度修改量。

具体的，梯度pl可以利用层析方程组线性近似得到：

其中，ha为近似hessian矩阵，δt为某一炮检对所对应的初至波到达时，δt1为第一炮检对所对应的初至波到达时，δti为第i炮检对所对应的初至波到达时，δtn为第n炮检对所对应的初至波到达时，k11为第1条射线在第1个模型网格内的长度，ki1为第i条射线在第1个模型网格内的长度，kn1为第n条射线在第1个模型网格内的长度，k1j为第1条射线在第j个模型网格内的长度，kij表示第i条射线在第j个模型网格内的长度，knj为第n条射线在第j个模型网格内的长度，k1m为第1条射线在第m个模型网格内的长度，kim为第i条射线在第m个模型网格内的长度，knm为第n条射线在第m个模型网格内的长度，k^t的每一列为一条射线路径。该表达式涉及到大型矩阵-向量乘运算，存储存在困难，可通过矩阵运算进行改写：

公式(3)中等式右端每一个列向量(ki1…kij…kim)^t即为某一炮检对所对应的射线路径。因此，不必再存储完整的矩阵k^t，仅需要存储单一炮检对所对应的射线路径即可实现梯度的计算，再用梯度乘以固定步长计算得出速度修改量，大大减少了内存的占用。近似hessian矩阵ha也可以用该方法进行计算，同时由于ha是主对角元素占优的矩阵，仅利用其对角元素就可以获得比较好的结果，所以利用它的对角阵ho的逆ho^-1来近似ha^-1，本发明最终采用的hessian矩阵表达式为：

其中，k11为第1条射线在第1个模型网格内的长度，ki1为第i条射线在第1个模型网格内的长度，kn1为第n条射线在第1个模型网格内的长度，k1j为第1条射线在第j个模型网格内的长度，kij表示第i条射线在第j个模型网格内的长度，knj为第n条射线在第j个模型网格内的长度，k1m为第1条射线在第m个模型网格内的长度，kim为第i条射线在第m个模型网格内的长度，knm为第n条射线在第m个模型网格内的长度，k1j为第1条射线在第j个模型网格内的长度，k1m为第1条射线在第m个模型网格内的长度，ki1为第i条射线在第1个模型网格内的长度，kim为第i条射线在第m个模型网格内的长度，kn1为第n条射线在第1个模型网格内的长度，knj为第n条射线在第j个模型网格内的长度，knm为第n条射线在第m个模型网格内的长度。

由此，避免了存储大型矩阵，仅存储每一个炮检对的射线路径即可实现梯度的计算，再用梯度乘以固定步长计算得出速度修改量，这种方法被称为改进散射积分算法。

公式(5)所示为炮检距与射线最大深度关系，

其中，x为炮检距，v0为地表速度，k为地下速度随深度的变化率，当逐步减小最大炮检距时，射线达到的深度逐渐变浅，可以减小最大炮检距反演对浅层的影响。

作为优选方案，通过模型迭代方法获得当前速度模型，模型迭代方法使用的公式为：

ml+1＝ml+αlpl(1)

其中，ml+1为当前速度模型，ml为初始速度模型，下标l为迭代进行到了第l轮，αlpl为速度修改量，pl为梯度，αl为固定步长。

根据本发明的多尺度近地表层析速度建模系统，该系统包括：存储器，存储有计算机可执行指令；处理器，处理器运行存储器中的计算机可执行指令，执行以下步骤：步骤1：输入初至波走时和初始速度模型；步骤2：基于初始速度模型计算理论走时和射线路径；步骤3：获得速度修改量，根据速度修改量，修改初始速度模型获得当前速度模型；步骤4：比较速度修改量与预设速度修改量阈值；步骤5：若速度修改量大于或等于预设速度修改量阈值，则比较最大炮检距与炮检距阈值；步骤6：若最大炮检距大于或等于炮检距阈值，则将当前速度模型作为最终速度模型。

作为优选方案，多尺度近地表层析速度建模系统，还包括：若速度修改量小于预设速度修改量阈值，则返回步骤2并将当前速度模型作为初始速度模型。

具体的，根据速度修改量与预设速度修改量阈值的比较结果，若速度修改量小于预设速度修改量阈值，返回步骤2，并将前速度模型作为初始速度模型，重新获取速度修改量，以及修改初始速度模型。

作为优选方案，所多尺度近地表层析速度建模系统，还包括：若最大炮检距小于炮检距阈值则返回步骤1，并减小最大炮检距，将当前速度模型作为初始速度模型。

具体的，根据最大炮检距与炮检距阈值的比较结果，若最大炮检距小于炮检距阈值，则返回步骤1，并减小最大炮检距，将当前速度模型作为初始速度模型，输入最大炮检距范围内的初至波走时，重新获取速度修改量，修改速度模型。

根据示例性的实施方式多尺度近地表层析速度建模系统通过若最大炮检距小于炮检距阈值，则减少最大炮检距，将当前速度模型作为初始速度模型，重新输入初至波走时，进行初始速度模型的修改，从而采用了多尺度反演策略，提高了反演精度，可建立高精度近地表速度模型。

作为优选方案，通过射线追踪法计算理论走时和射线路径。

作为优选方案，通过改进散射积分算法获得速度修改量。

根据示例性的实施方式多尺度近地表层析速度建模系统通过改进散射积分算法获得速度修改量，该方法计算速度快、内存占用小，提高了反演效率，可进行大规模三维近地表速度建模。

作为优选方案，通过改进散射积分算法获得速度修改量，包括：存储单一炮检对的射线路径，计算梯度；根据梯度，获取速度修改量。

具体的，梯度pl可以利用层析方程组线性近似得到：

其中，ha为近似hessian矩阵，δt为某一炮检对所对应的初至波到达时，δt1为第一炮检对所对应的初至波到达时，δti为第i炮检对所对应的初至波到达时，δtn为第n炮检对所对应的初至波到达时，k11为第1条射线在第1个模型网格内的长度，ki1为第i条射线在第1个模型网格内的长度，kn1为第n条射线在第1个模型网格内的长度，k1j为第1条射线在第j个模型网格内的长度，kij表示第i条射线在第j个模型网格内的长度，knj为第n条射线在第j个模型网格内的长度，k1m为第1条射线在第m个模型网格内的长度，kim为第i条射线在第m个模型网格内的长度，knm为第n条射线在第m个模型网格内的长度，kij为第i条射线在第j个模型网格内的长度，故k^t的每一列为一条射线路径。该表达式涉及到大型矩阵-向量乘运算，存储存在困难，可通过矩阵运算进行改写：

公式(3)中等式右端每一个列向量(ki1…kij…kim)^t即为某一炮检对所对应的射线路径。因此，不必再存储完整的矩阵k^t，仅需要存储单一炮检对所对应的射线路径即可实现梯度的计算，再用梯度乘以固定步长计算得出速度修改量，大大减少了内存的占用。近似hessian矩阵ha也可以用该方法进行计算，同时由于ha是主对角元素占优的矩阵，仅利用其对角元素就可以获得比较好的结果，所以利用它的对角阵ho的逆ho^-1来近似ha^-1，本发明最终采用的hessian矩阵表达式为：

其中，k11为第1条射线在第1个模型网格内的长度，ki1为第i条射线在第1个模型网格内的长度，kn1为第n条射线在第1个模型网格内的长度，k1j为第1条射线在第j个模型网格内的长度，kij表示第i条射线在第j个模型网格内的长度，knj为第n条射线在第j个模型网格内的长度，k1m为第1条射线在第m个模型网格内的长度，kim为第i条射线在第m个模型网格内的长度，knm为第n条射线在第m个模型网格内的长度，k1j为第1条射线在第j个模型网格内的长度，k1m为第1条射线在第m个模型网格内的长度，ki1为第i条射线在第1个模型网格内的长度，kim为第i条射线在第m个模型网格内的长度，kn1为第n条射线在第1个模型网格内的长度，knj为第n条射线在第j个模型网格内的长度，knm为第n条射线在第m个模型网格内的长度。

由此，避免了存储大型矩阵，仅存储每一个炮检对的射线路径即可实现梯度的计算，再用梯度乘以固定步长计算得出速度修改量，这种方法被称为改进散射积分算法。

公式(5)所示为炮检距与射线最大深度关系，

其中，x为炮检距，v0为地表速度，k为地下速度随深度的变化率，当逐步减小最大炮检距时，射线达到的深度逐渐变浅，可以减小最大炮检距反演对浅层的影响。

作为优选方案，通过模型迭代方法获得当前速度模型，模型迭代方法使用的公式为：

ml+1＝ml+αlpl(1)

其中，ml+1为当前速度模型，ml为初始速度模型，下标l为迭代进行到了第l轮，αlpl为速度修改量，pl为梯度，αl为固定步长。

实施例

图1示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的流程图。

如图1所示，多尺度近地表层析速度建模方法，包括：

步骤1：输入初至波走时和初始速度模型；

步骤2：基于初始速度模型计算理论走时和射线路径；

其中，通过射线追踪法计算理论走时和射线路径；

步骤3：获得速度修改量，根据速度修改量，修改初始速度模型获得当前速度模型；

其中，通过模型迭代方法获得当前速度模型，模型迭代方法使用的公式为：

ml+1＝ml+αlpl(1)

其中，ml+1为当前速度模型，ml为初始速度模型，下标l为迭代进行到了第l轮，αlpl为速度修改量，pl为梯度，αl为固定步长；

其中，通过改进散射积分算法获得速度修改量；

其中，通过改进散射积分算法获得速度修改量，包括：存储单一炮检对的射线路径，计算梯度；根据梯度，获取速度修改量；

具体的，梯度pl可以利用层析方程组线性近似得到：

其中，ha为近似hessian矩阵，δt为某一炮检对所对应的初至波到达时，δt1为第一炮检对所对应的初至波到达时，δti为第i炮检对所对应的初至波到达时，δtn为第n炮检对所对应的初至波到达时，k11为第1条射线在第1个模型网格内的长度，ki1为第i条射线在第1个模型网格内的长度，kn1为第n条射线在第1个模型网格内的长度，k1j为第1条射线在第j个模型网格内的长度，kij表示第i条射线在第j个模型网格内的长度，knj为第n条射线在第j个模型网格内的长度，k1m为第1条射线在第m个模型网格内的长度，kim为第i条射线在第m个模型网格内的长度，knm为第n条射线在第m个模型网格内的长度，kij为第i条射线在第j个模型网格内的长度，故k^t的每一列为一条射线路径。该表达式涉及到大型矩阵-向量乘运算，存储存在困难，可通过矩阵运算进行改写：

公式(3)中等式右端每一个列向量(ki1…kij…kim)^t即为某一炮检对所对应的射线路径。因此，不必再存储完整的矩阵k^t，仅需要存储单一炮检对所对应的射线路径即可实现梯度的计算，再用梯度乘以固定步长计算得出速度修改量，大大减少了内存的占用。近似hessian矩阵ha也可以用该方法进行计算，同时由于ha是主对角元素占优的矩阵，仅利用其对角元素就可以获得比较好的结果，所以利用它的对角阵ho的逆ho^-1来近似ha^-1，本发明最终采用的hessian矩阵表达式为：

其中，k11为第1条射线在第1个模型网格内的长度，ki1为第i条射线在第1个模型网格内的长度，kn1为第n条射线在第1个模型网格内的长度，k1j为第1条射线在第j个模型网格内的长度，kij表示第i条射线在第j个模型网格内的长度，knj为第n条射线在第j个模型网格内的长度，k1m为第1条射线在第m个模型网格内的长度，kim为第i条射线在第m个模型网格内的长度，knm为第n条射线在第m个模型网格内的长度，k1j为第1条射线在第j个模型网格内的长度，k1m为第1条射线在第m个模型网格内的长度，ki1为第i条射线在第1个模型网格内的长度，kim为第i条射线在第m个模型网格内的长度，kn1为第n条射线在第1个模型网格内的长度，knj为第n条射线在第j个模型网格内的长度，knm为第n条射线在第m个模型网格内的长度。

由此，避免了存储大型矩阵，仅存储每一个炮检对的射线路径即可实现梯度的计算，再用梯度乘以固定步长计算得出速度修改量，这种方法被称为改进散射积分算法。

步骤4：比较速度修改量与预设速度修改量阈值；

其中，若速度修改量小于预设速度修改量阈值，则返回步骤2并将当前速度模型作为初始速度模型；

步骤5：若速度修改量大于或等于预设速度修改量阈值，则比较最大炮检距与炮检距阈值；

其中，若最大炮检距小于炮检距阈值，则返回步骤1，并减小最大炮检距，将当前速度模型作为初始速度模型；

步骤6：若最大炮检距大于或等于炮检距阈值，则将当前速度模型作为最终速度模型。

图2示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的真实速度模型。图3示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的初始速度模型。

如图2所示，设计一个空间网格数1447*1201*400，网格间距为10m的三维速度模型，截取其中y＝6500m处的速度模型。

如图3所示，初始速度模型是速度随着深度增加的梯度模型，以便产生潜水波。在图2-图3，纵坐标表示模型深度(km)，横坐标表示模型长度(km)。

图4和图5分别示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的全数据层析速度模型和多尺度层析速度模型。

如图4和图5所示，分别为全数据层析速度模型反演结果和分尺度层析速度模型反演结果，通过对比，可以看出分尺度反演策略的实施使得近地表信息更加丰富。在图4-图5，纵坐标表示模型深度(km)，横坐标表示模型长度(km)。

图6a、图6b、图6c分别示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的地下50m深度、100m深度和150m深度的反演结果。

如图6a、图6b和图6c所示，为地下不同深度的反演结果对比，可以看出改进的散射积分法初至波走时层析可以反映速度的宏观变化，同时多尺度反演策略的使用可以有效提高反演精度。在图6a-图6c，纵坐标表示不同模型的速度值(m/s)，横坐标表示模型长度(km)。

图7a、图7b和图7c分别示出了根据本发明的一个实施例的一种多尺度近地表层析速度建模方法的横向距离5km、7km、9km的反演结果。

如图7a、图7b和图7c所示，为横向不同位置的反演结果对比，可以看出改进的散射积分法初至波走时层析可以反映速度的宏观变化，同时多尺度反演策略的使用可以有效提高近地表的反演精度，但是对深部影响不大。在图7a-图7c，纵坐标表示模型深度(km)，纵坐标表示不同模型的速度值(m/s)。

以上已经描述了本发明的各实施例，上述说明是示例性的，并非穷尽性的，并且也不限于所披露的各实施例。在不偏离所说明的各实施例的范围和精神的情况下，对于本技术领域的普通技术人员来说许多修改和变更都是显而易见的。