预应力混凝土桥梁腐蚀疲劳寿命预测方法与流程

本发明涉及服役桥梁安全评估领域，特别是一种预应力混凝土桥梁腐蚀疲劳寿命预测方法。

背景技术

预应力混凝土桥梁跨越能力强，在我国公路桥梁中占很大比重。近年来，该类桥梁的耐久性问题逐渐显现。对于后张预应力混凝土梁，施工工艺要求预应力筋张拉后需进行孔道压浆。然而，早期修建的后张预应力混凝土桥梁，由于施工缺陷、泌水等原因，预应力混凝土梁孔道压浆不饱满的问题较为普遍。压浆不饱满会加速腐蚀离子侵入并导致钢绞线腐蚀，降低预应力钢绞线和混凝土间的协同工作性。同时，服役桥梁还承受反复的车辆荷载，随着经济的发展，交通量和轴重呈上升趋势。腐蚀减小了钢绞线截面积，钢绞线承受的实际应力幅增大，腐蚀和疲劳的共同作用加速了材料的疲劳损伤累积，结构失效概率显著增加。

目前，对预应力混凝土桥梁的疲劳剩余寿命预测多是基于疲劳试验数据得到的经验公式，未考虑材料性能退化和钢绞线应力增长等因素，缺乏定量的评价标准。后张预应力混凝土桥梁中的钢绞线锈蚀后，其应力状态更加复杂，疲劳损伤参量的确定难度加大。预应力混凝土桥梁的腐蚀疲劳主要失效形式为混凝土拉压疲劳破坏，钢绞线和普通钢筋疲劳失效。随着锈蚀程度的增加，不同失效形式可能发生转变。疲劳寿命预测分析中如何有效考虑结构剩余预加力、钢绞线锈蚀引起的应力集中及混凝土材料性能退化等因素亟待解决。

技术实现要素：

本发明所要解决的技术问题是，针对现有技术不足，提供一种预应力混凝土桥梁腐蚀疲劳寿命预测方法。

为解决上述技术问题，本发明所采用的技术方案是：一种预应力混凝土桥梁腐蚀疲劳寿命预测方法，包括以下步骤：

步骤一：计算疲劳荷载下受压区混凝土的弹性应变与塑性应变、计算退化后的混凝土弹性模量；

步骤二：采用锈蚀电流密度表征钢绞线的锈蚀速率，预测钢绞线的锈蚀损失，由此计算钢绞线剩余有效预加力；根据变形协调条件，考虑混凝土弹性模量退化，融入坑蚀导致的应力集中对钢绞线应变增长的影响，计算疲劳荷载引起的钢绞线弹性应变；考虑受压区混凝土塑性应变对钢绞线应变的影响，计算钢绞线塑性应变，得到锈蚀和疲劳共同作用下钢绞线应力；

步骤三：考虑钢绞线张拉锚固后对受拉区普通钢筋预压力的影响，得到受拉区普通钢筋初始应力；计算疲劳荷载作用下受拉区普通钢筋弹性应力；考虑受压区混凝土塑性应变对受拉区钢筋应变的影响，计算钢筋塑性应力，得到锈蚀和疲劳共同作用下受拉区钢筋总应力；

步骤四：随疲劳荷载次数的增加，对混凝土、受拉区钢筋、钢绞线的应力-应变进行实时计算，结合混凝土、普通钢筋、钢绞线的应力-应变增长关系模型和失效准则，判定结构失效模式，对结构疲劳寿命做出评价。

步骤一包括，

在疲劳荷载作用下，受压区混凝土的应变包括弹性应变和塑性应变

首先，计算受压区混凝土顶部的弹性应变为：

式中，和分别为经历n-1次疲劳后的混凝土弹性模量和钢绞线有效张拉力引起的弯矩效应；xn和分别为n次疲劳后车辆荷载引起的截面弯矩效应、受压区高度和开裂截面惯性矩，其中xn可参照部分预应力混凝土受弯构件中受压区高度的计算方法。

开裂截面惯性矩可表示为：

式中，b为截面宽度；yn为n次疲劳后开裂截面中性轴与混凝土受压区边缘的距离；hs、hp和a′s分别为受拉区普通钢筋、钢绞线和受压区普通钢筋的截面重心至混凝土受压区边缘的距离(假定受力筋在直径方向截面损失相同，则hs、hp和a′s在疲劳周期内为定值)；和分别为n次疲劳后，钢绞线与混凝土弹性模量比值、普通钢筋与混凝土弹性模量的比值；和分别为钢绞线、受拉区普通钢筋和受压区普通钢筋有效剩余面积。

其次，计算n次疲劳后受压区混凝土顶部应力相关系数αr,n：

式中，和分别为n次疲劳后受压区混凝土顶部的最大和最小弹性应力，

受压区混凝土顶部的累积塑性应变为：

式中，为混凝土轴心抗压强度初始实测值；为混凝土弹性模量初始实测值；ni为第i级疲劳荷载作用次数，(n与车辆荷载有关，为t的函数)。

然后，得到n次疲劳后混凝土的弹性模量：

式中，为n次疲劳荷载后混凝土弹性模量；修正系数β为统计结果(c20～c50为0.61，c60～c70为0.875)；其余符号含义同上。

受压区混凝土失效准则为：

式中，εc0为静载作用下混凝土的极限压应变。

所述的方法，所述的步骤二包括，

在疲劳荷载作用下，钢绞线的峰值应力分三部分：t时刻钢绞线剩余有效预加力引起的初始拉应力坑蚀所致应力集中和疲劳荷载引起的弹性应力和受压区混凝土塑性变形引起的应力

质量锈蚀率可表示为：

式中，iccor为锈蚀电流密度；l为锈蚀长度；r是结构中不同钢筋种类的锈蚀变异系数，对于钢绞线，r＝1。

t时刻剩余有效预加力为：

式中，ep和εp分别为未锈钢绞线的弹性模量和应变，t0为初始张拉力。

在疲劳荷载作用下，锈蚀钢绞线会在其坑蚀位置产生疲劳裂纹，裂纹不断扩展直至断裂。若经历n次疲劳荷载后钢绞线断裂，此时钢绞线有效剩余面积为则钢绞线总损失面积为记第n次荷载下钢绞线承受的最大应力为σp,max,n，则钢绞线在该特征荷载下疲劳断裂时的有效面积为：

式中，fu为预应力钢绞线的极限抗拉强度。

假定疲劳荷载下钢绞线的面积呈线性减小，经历n次疲劳数后，钢绞线剩余有效面积为：

式中，nk-1为第k-1次疲劳时钢绞线应力幅所对应的钢绞线s-n曲线中的寿命值。

在t时刻，剩余有效预加力引起的钢绞线拉应力为：

钢绞线剩余有效面积的减小以及受压区混凝土弹性模量的退化会导致应力重分布，受压区高度、钢绞线和普通钢筋的应力-应变关系则相应发生变化。

疲劳荷载引起的钢绞线弹性为：

式中，kt为锈坑引起的应力集中系数。

经历n次疲劳后，受压区边缘混凝土塑性应变为受压区高度为xn。由平截面假定、混凝土与钢绞线的变形协调条件可得到引起的钢绞线塑性应变：

受压区混凝土塑性变形引起的钢绞线应力为：

即，钢绞线应力可表示为：

钢绞线失效准则为：

所述的方法，所述的步骤三包括，

在疲劳荷载作用下，受拉区普通钢筋峰值应力分为三部分：t时刻钢绞线剩余有效预加力引起的普通钢筋压应力疲劳荷载引起的弹性应力和受压区混凝土塑性变形引起的应力

由于在计算混凝土弹性应变过程中，已考虑了钢绞线有效预加力的作用效应(即)，为避免重复计算，记为0。

疲劳荷载引起的受拉区普通钢筋弹性应力为：

由平截面假定、混凝土与普通钢筋的变形协调条件可得到引起的受拉区普通钢筋塑性应变：

受压区混凝土塑性变形引起的受拉区普通钢筋应力为：

受拉区普通钢筋应力为：

普通钢筋的失效准则为：

式中，fy为普通钢筋的屈服强度。

所述的方法，所述的步骤四包括，

预应力混凝土桥梁的疲劳寿命计算流程如下：首先，对于给定的n，将混凝土、钢绞线和受拉钢筋的应力计算式(5)、(15)和(20)代入平衡方程(内力平衡方程、力矩平衡方程)即可解出相应的应力大小；其次，分别根据公式(6)、(16)、(21)中各组成材料的失效判别准则，判别结构是否疲劳失效；若未失效，则增大n，重复以上步骤；如此往复，进行循环迭代计算，直至一种材料失效，此时所经历的疲劳次数n即为结构的疲劳寿命。

本发明的技术效果在于，针对压浆不饱满的预应力混凝土桥梁结构，考虑钢绞线锈蚀、应力集中、混凝土弹性模量退化和残余应变等因素，分别将钢绞线和普通钢筋的峰值应力分为三部分，提出了二者应力增长模型；融入车辆荷载，形成了一整套腐蚀环境和荷载作用下预应力混凝土桥梁疲劳寿命分析方法。本发明预测方法合理，适用性强，更加接近实际桥梁的损伤演化，可为服役预应力混凝土桥梁的疲劳寿命评估提供支持。

附图说明

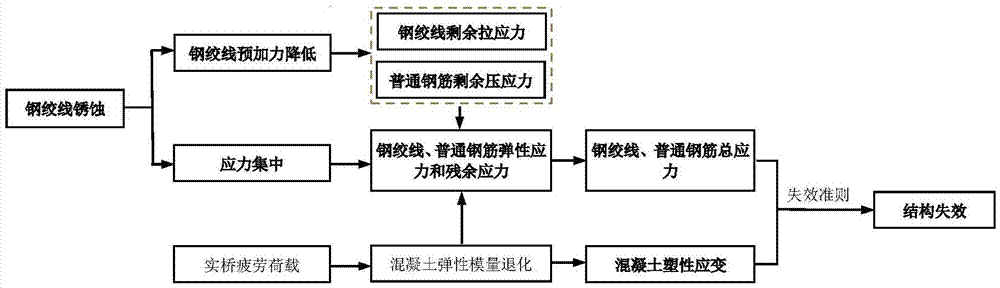
图1为本发明的疲劳寿命评估整体示意图。

图2为混凝土、普通钢筋和钢绞线应变示意图。图2中，为剩余有效预加力作用下钢绞线应变；和分别为疲劳荷载作用下钢绞线和普通钢筋弹性应变；和分别为受压区混凝土塑性变形引起的钢绞线和普通钢筋塑性应变。

图3为发明的计算流程图。

具体实施方式

(1)确定疲劳荷载下受压区混凝土弹性应变

首先，计算受压区混凝土顶部的弹性应变为：

式中，和分别为经历n-1次疲劳后的混凝土弹性模量和钢绞线有效张拉力引起的弯矩效应；xn和分别为n次疲劳后车辆荷载引起的截面弯矩效应、受压区高度和开裂截面惯性矩，其中xn可参照部分预应力混凝土受弯构件中受压区高度的计算方法。

开裂截面惯性矩可表示为：

式中，b为截面宽度；yn为n次疲劳后开裂截面中性轴与混凝土受压区边缘的距离；hs、hp和a′s分别为受拉区普通钢筋、钢绞线和受压区普通钢筋的截面重心至混凝土受压区边缘的距离(假定受力筋在直径方向截面损失相同，则hs、hp和a′s在疲劳周期内为定值)；和分别为n次疲劳后，钢绞线与混凝土弹性模量比值、普通钢筋与混凝土弹性模量的比值；和分别为钢绞线、受拉区普通钢筋和受压区普通钢筋有效剩余面积。

计算n次疲劳后受压区混凝土顶部应力相关系数αr,n：

式中，和分别为n次疲劳后受压区混凝土顶部的最大和最小弹性应力，

受压区混凝土顶部的累积塑性应变为：

式中，为混凝土轴心抗压强度初始实测值；为混凝土弹性模量初始实测值；ni为第i级疲劳荷载作用次数，(n与车辆荷载有关，为t的函数)。

然后，得到n次疲劳后混凝土的弹性模量：

式中，为n次疲劳荷载后混凝土弹性模量；修正系数β为统计结果(c20～c50为0.61，c60～c70为0.875)；其余符号含义同上。

当混凝土累积塑性应满足下式时，即判断混凝土压溃，结构即丧失继续承载的能力：

式中，εc0为静载作用下混凝土的极限压应变。

(2)确定钢绞线锈蚀后剩余有效预加力

钢绞线在腐蚀环境下会形成微弱的腐蚀电流，用腐蚀电流表示的钢绞线锈蚀率为：

式中，iccor为锈蚀电流密度；l为锈蚀长度；r是结构中不同钢筋种类的锈蚀变异系数，对于钢绞线，r＝1。

钢绞线面积损失会导致预加力的降低，t时刻钢绞线剩余有效预加力tρm,t为：

式中，ep和εp分别为未锈钢绞线的弹性模量和应变，t0为初始张拉力。

(3)确定疲劳荷载下钢绞线的剩余有效面积

在疲劳荷载作用下，锈蚀钢绞线会在其坑蚀位置产生疲劳裂纹，裂纹不断扩展直至断裂。若经历n次疲劳荷载后钢绞线断裂，此时钢绞线有效剩余面积为则钢绞线总损失面积为记第n次荷载下钢绞线承受的最大应力为σp,max,n，则钢绞线在该特征荷载下疲劳断裂时的有效面积为：

式中，fu为预应力钢绞线的极限抗拉强度。

假定疲劳荷载下钢绞线的面积呈线性减小，经历n次疲劳数后，钢绞线剩余有效面积为：

式中，nk-1为第k-1次疲劳时钢绞线应力幅所对应的钢绞线s-n曲线中的寿命值。

(4)确定钢绞线应力峰值的三个部分

将钢绞线的应力峰值分为三部分：t时刻剩余有效预加力tρm,t引起的拉应力疲劳荷载及坑蚀所致应力集中引起的弹性应力和受压区混凝土塑性变形引起的应力

在t时刻，剩余有效预加力引起的钢绞线拉应力为：

钢绞线剩余有效面积的减小以及受压区混凝土弹性模量的退化会导致应力重分布，受压区高度、钢绞线和普通钢筋的应力-应变关系则相应发生变化。

疲劳荷载引起的钢绞线弹性为：

式中，kt为锈坑引起的应力集中系数。

经历n次疲劳后，受压区边缘混凝土塑性应变为受压区高度为xn。由平截面假定、混凝土与钢绞线的变形协调条件可得到引起的钢绞线塑性应变：

受压区混凝土塑性变形引起的钢绞线应力为：

即，钢绞线应力可表示为：

钢绞线失效准则为：

(5)确定普通钢筋应力峰值的三个部分

将受拉区普通钢筋峰值应力分为三部分：t时刻钢绞线剩余有效预加力tρm,t引起的普通钢筋压应力σs,0、疲劳荷载引起的弹性应力和受压区混凝土塑性变形引起的应力

由于在计算混凝土弹性应变过程中，已考虑了钢绞线有效预加力的作用效应(即)，为避免重复计算，记为0。

疲劳荷载引起的受拉区普通钢筋弹性应力为：

由平截面假定、混凝土与普通钢筋的变形协调条件可得到引起的受拉区普通钢筋塑性应变：

受压区混凝土塑性变形引起的受拉区普通钢筋应力为：

受拉区普通钢筋应力为：

普通钢筋的失效准则为：

式中，fy为普通钢筋的屈服强度。

(6)确定结构失效模式，预测疲劳寿命

预应力混凝土桥梁的疲劳寿命计算流程如下：首先，对于给定的n，将混凝土、钢绞线和普通钢筋的应力计算式(5)、(15)和(20)代入平衡方程(内力平衡方程、力矩平衡方程)即可解出相应的应力大小；其次，分别根据公式(6)、(16)、(21)中各组成材料的失效判别准则，判别结构是否疲劳失效；若未失效，则增大n，重复以上两个计算步骤；如此往复，进行循环迭代计算，直到以上三种构成材料的其中之一达到失效准则，则结构失效，此时结构经历的荷载循环次数n即为结构可以承受的疲劳次数，n对应的时间t即为结构的疲劳寿命。