一种高精度大气折射率误差计算方法与流程

本发明涉及电波折射率计算领域，具体涉及一种高精度大气折射率误差计算方法。

背景技术：

在现代战争中，雷达是不可或缺的一种探测设备，高精度的雷达不仅可以对目标进行精确的定位和测速，而且也能够对目标进行准确识别，从而为攻击和防御系统的有效运行奠定坚实的基础。在雷达从地面对空中目标的探测中，雷达无线电信道是空中大气，由于空中大气是折射率不等于1的不均匀媒质，因此雷达在工作中，其电波必定会产生折射效应，从而使得电波射线产生弯曲、传播速度小于光速、多普勒频率不再正比于目标的径向速度等现象，最终导致雷达在对目标的探测中产生折射误差。为了提高雷达的探测精度，必须对引起大气折射的误差的大气折射率进行计算，其计算精度将直接影响雷达对目标的定位和测速精度。

决定大气折射误差的主要因素有两个，一个电波折射修正算法误差，或称为公式误差，另一个是电波折射修正中采用的空中大气折射率剖面(随高度变化)误差，或称为大气折射率误差。经过几十年的研究，电波折射修正的公式误差已很小，常用的以电波射线描迹法为代表的电波折射修正算法已具有很高的精度。目前限制电波折射误差修正精度的主要因素是大气折射率误差，由于大气折射率误差在实际的空间环境中大气是分层的，所以电磁波在传播时其传播射线要发生不同程度的弯曲，由斯奈尔定律可知，雷达电波射线上大气折射率的准确性是影响电波折射误差修正精度的关键因素之一。这就需要在实际应用中精确获得雷达电波射线处的大气折射率。目前大气折射率剖面的获取方法较多，按种类分主要有直接探测法、模式法和反演法等三种。直接探测法主要是在雷达所在地采用五九型探空仪、电子探空仪、adas探测系统等进行不同高度处的大气温度、气压湿度等参数探测，然后利用大气折射率与温度、气压和湿度的函数关系计算出对应高度处的大气折射率值，从而获得雷达所在地的大气折射率剖面，称为离散剖面；模式法是对雷达所占地的大气折射率剖面进行多次探测，然后对这些数据进行统计，获得该地的大气折射率模型；反演法是利用微波辐射计或gps等在雷达所占地进行测量，进而反演出该地的大气折射率剖面。这三类方法相比，直接探测法获得大气折射率剖面的精度最高，这也是高精度电波折射修正中采用该方法获得大气折射率剖面的缘故。

在大气折射率的直接探测法中，探测器一般由氢气球或氦气球携带自由升空，探测器每隔10秒左右发出一组大气参数，因此采用直接探测法获得的大气折射率剖面是一不等高度间隔的离散数据，即不同的离地高度与相应高度处的大气折射率值。在电波折射修正中，为了确保计算精度，一般描迹电波射线的步长很短，这样电波折射计算中用到的各点处大气折射率需要通过对已获得的大气离散剖面进行插值得到。目前在应用于电波折射修正中的大气折射率的所有插值方法中，都采用线性插值算法，即没有实测值的折射率由该高度前后两个相邻有实测值进行线性插值得到。根据大气折射率随高度的变化规律可知，大气折射率随高度一般分为三段变化，第一段(地面到离地1km范围)的大气折射率随高度呈线性衰减，第二段(地面1km到海拔9km范围)和第三段(海拔9km到对流层顶60km)的大气折射率随高度呈指数衰减，但是这两段大气的指数衰减系数不同。如果在电波折射修正中，第一段大气电波射线上的折射率采用线性插值其精度是较高的，但是在第二或第三段大气采用线性插值，由于大气直接探测得到的离散数据的相邻高度一般都在几百米或几千米，线性插值与实际大气折射率变化规律不相符，因此会产生较大的误差，进而影响电波折射修正精度，最终影响雷达的探测精度。

技术实现要素：

本发明的目的在于提供一种高精度大气折射率误差计算方法，能够降低大气折射率的误差，提高大气折射率的计算精度。

为实现上述目的，本发明采用如下技术方案：

一种高精度大气折射率误差计算方法，包括：

①在地面到离地1km的范围内，大气折射率呈线性衰减，当目标高度在此范围内时，利用线性插值法得到该目标的大气折射率；

②在离地面1km以上的范围内，大气折射率成指数衰减，当目标高度为离地1km到最大实测探空离散数据最高处ht范围内时，首先计算出离地1km处的大气折射率n1，其对应的海拔高度为hs+1，并假设大于hs+1高度的第一个实测大气折射率剖面的高度为hk+1，高度hk+1处对应的大气折射率为nk+1，令hs+1高度处的大气折射率为nk，nk＝n1，并令hs+1＝hk，然后计算出实测探空离散数据中相邻两高度hk和hk+1之间的衰减系数ck，即

对于高度hk和高度hk+1范围内不同高度对应的大气折射率ni采用如下公式得到

其中，hi表示目标高度，下标t和s均为区分作用，并非变量；

③当目标高度大于实测探空离散数据最高处ht以上范围时，由于此部分没有实测数据，而只能用全国大气探测数据统计结果，即c9＝0.1424，对于该部分大气折射率，首先由式(1)和式(2)计算出海拔9km高度处的大气折射率n9，然后根据公式(3)计算出该范围内任意高度的大气折射率ni，即

④分别基于步骤①、步骤②和步骤③得到的大气折射率进行电波折射误差计算，从而得出目标的误差。

优选的，所述①中，利用线性插值法计算大气折射率时，假设目标高度hi处的大气折射率为ni，而ni处于实测大气折射率剖面中的高度hj和hj+1之间，它们对应的大气折射率分别为nj和nj+1，则采用线性插值可得到：

其中，nj和nj+1均可根据大气折射率剖面中获取，其均为现有数据，i＝1，2，3…；j＝1，2，3…；

利用(4)式可以得到地面到离地1km的范围内的各个高度上的大气折射率值。

优选的，所述④中，若目标处在低于60km的低层大气中，根据雷达测量目标的视在距离的定义和其相关的几何关系可得出以下数学表达式：

式中，re表示雷达的视在距离，c表示无折射的真空速度，t表示电波在低层大气中的传播时间，h0表示雷达观测站的海拔高度，ht表示实测大气折射率剖面的最高高度，n表示目标高度hi的大气折射指数，n＝1+n×10^-6，cscθ的值可由斯奈尔定律变形得出，hi表示的是在不大于实测大气折射率剖面最高高度以内的目标高度，下标e、0、t和i均为区分作用，并非变量；

令任意高度上的矢径数值为r＝a+h，雷达测量站至地心的距离是r0＝a+h0，r表示当地的地球半径，a表示地球的地球半径，h表示当地在电波射线轨迹上的海拔高度，h0表示雷达观测站的海拔高度，因此斯奈尔定律可写为：

n(a+h)cosθ＝n0(a+h0)cosθ0(6)

则：

将式(7)代入式(5)中，即可得到雷达的视在距离为：

地心张角与海拔高度h的关系为：

将上式左右两边同时进行积分，得：

其中，θ0表示雷达的视在仰角θ0，θ表示在海拔h处的射线的仰角；

根据三角形正弦定理知：

其中，α0表示目标的真实仰角，表示地心张角；

由式(11)可得目标的真实仰角α0为：

再次由正弦定理可知：

从而可推导出雷达观测站到目标的真实距离为：

已知雷达的视在距离re、视在仰角θ0，以及目标的真实仰角α0、真实距离r0，可以得出目标的距离的误差δr及仰角的误差ε，即：

以上，h为电波射线轨迹上某点的地面高度，是个变量，h0代表雷达观测站的海拔高度，hi是目标高度，hs为地面海拔高度，主要用于大气折射率指数模型，hk表示实测大气折射率剖面数据中的某个值。

本发明根据大气折射率随高度变化的规律，在地面到离地面1km的范围内利用线性插值法计算大气折射率，在离地面1km以上的范围内利用指数插值法计算大气折射率，并利用该大气折射率计算出目标的误差。本发明能够降低大气折射率的误差，提高大气折射率的计算精度，从而提高雷达对目标的定位和测速精度。

附图说明

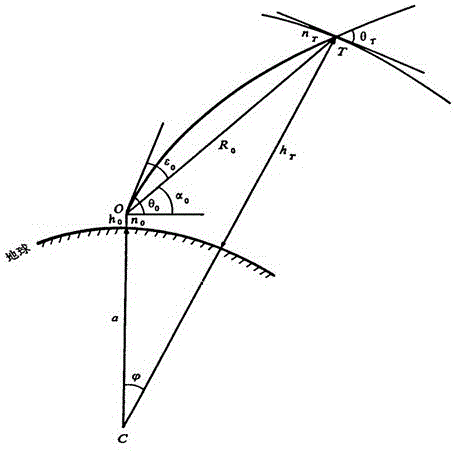
图1为本发明所述射线描迹法中电波传播射线的路径图；

图2为本发明所述实施例中的目标飞行航迹图；

图3为本发明所述实施例中不同海拔高度的大气折射率图。

具体实施方式

以下结合附图对本发明的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明的部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动的前提下所获得的其他所有实施例，都属于本发明的保护范围。

由于电波在大气传播时会发生折射现象，所以通常用射线来表示电波传播的轨迹，大气折射率剖面是描述大气折射率沿高度变化的数学公式或相关数据，因此计算大气折射率剖面时，需要首先计算电波传播的射线轨道，在本实施例中采用射线描迹法进行计算，具体计算过程如下：

如图1所示，已知射线初始位置上的大气折射指数n0、矢径r0和初始仰角θ0，则由斯奈尔定律的变形式可得出：

θ表示目标在海拔h处电波射线上的仰角，n表示大气折射指数，r表示当地地球半径；

根据三角关系，可推导出：

在图1中，假设射线上某点的位置用水平距离d和高度h表示，当该点沿射线移动到另外一点时，则该点的半径和高度都会有所变化，即：

其中，是地心张角的微变量，根据数学几何关系有：

其中，dd是水平距离d的微变量，结合式(19)和使(20)，根据图1可知r＝r0+h，则有：

将等式两边同时求积分，则当海拔高度h取0至ht时所对应地面距离d可表示为：

其中，ht表示实测大气折射率剖面最高高度，下标t为区分作用，并非变量，由上式得知，d是ht的函数，当高度h连续做微小的变化，即h依次取0、δh、2δh、…、nδh时，根据上述函数关系式可得到高度对应的地面距离d分别为0、d1、d21、…、dn，当δh→h时，相邻的离散点可视为连续，进而形成了射线轨道，δh为随机选取的数据，表示高度h的变化量。

大气折射率随高度分布的模型为：

式(16)中，h表示电波射线轨迹上的目标海拔高度，n(h)为海拔h处的大气折射率，ns和hs分别为地面大气折射率和海拔高度，g为海拔hs到海拔hs+1之间的大气折射率垂直梯度，1/km；n1为海拔hs+1处的大气折射率；c1为海拔hs+1与海拔9km之间大气衰减系数，1/km；n9为海拔9km高度处的大气折射率；c9为海拔9km以上高度的大气衰减系数，1/km；在地面到离地1km范围内，大气折射率呈线性衰减，在这一范围内的大气折射率可采用线性插值方法得到；在地面1km到海拔9km和海拔9km到海拔60km高度范围内，大气折射率都呈指数衰减，在这一范围内的大气折射率可采用指数插值方法得到，其中，下标s为区分作用，并非变量。

基于此，本发明提供了一种高精度大气折射率误差计算方法，包括：

①在地面到离地1km的范围内，大气折射率呈线性衰减，当目标高度在此范围内时，利用线性插值法得到该目标的大气折射率；

利用线性插值法计算大气折射率时，假设目标高度hi处的大气折射率为ni，而ni处于实测大气折射率剖面中的高度hj和hj+1之间，它们对应的大气折射率分别为nj和nj+1，则采用线性插值可得到：

其中，nj和nj+1均可根据大气折射率剖面中获取，其均为现有数据，i＝1，2，3…；j＝1，2，3…；

利用(4)式可以得到地面到离地1km的范围内的各个高度上的大气折射率值。

②在离地面1km以上的范围内，大气折射率成指数衰减，当目标高度为离地1km到最大实测探空离散数据最高处ht范围内时，首先计算出离地1km处的大气折射率n1，其对应的海拔高度为hs+1，假设大于hs+1高度的第一个实测大气折射率剖面的高度为hk+1，高度hk+1处对应的大气折射率为nk+1，令hs+1高度处的大气折射率为nk，nk＝n1，并令hs+1＝hk，然后计算出实测探空离散数据中相邻两高度hk和hk+1之间的衰减系数ck，即

对于高度hk和高度hk+1范围内不同高度对应的大气折射率ni采用如下公式得到

其中，hi表示目标高度，下标t和s均为区分作用，并非变量；

③当目标高度大于实测探空离散数据最高处ht以上范围时，由于此部分没有实测数据，而只能用全国大气探测数据统计结果，即c9＝0.1424，对于该部分大气折射率，首先由式(1)和式(2)计算出海拔9km高度处的大气折射率n9，然后根据公式(3)计算出该范围内任意高度的大气折射率ni，即

④分别基于步骤①、步骤②和步骤③得到的大气折射率进行电波折射误差计算，从而得出目标的误差。

若目标处在低于60km的低层大气中，根据雷达测量目标的视在距离的定义和其相关的几何关系可得出以下数学表达式：

式中，re表示雷达的视在距离，c表示无折射的真空速度，t表示电波在低层大气中的传播时间，h0表示雷达观测站的海拔高度，ht表示实测大气折射率剖面的最高高度，n表示目标高度hi的大气折射指数，n＝1+n×10^-6，cscθ的值可由斯奈尔定律变形得出，hi表示的是在不大于实测大气折射率剖面最高高度以内的目标高度，下标e、0、t和i均为区分作用，并非变量；

令任意高度上的矢径数值为r＝a+h，雷达测量站至地心的距离是r0＝a+h0，r表示当地的地球半径，a表示地球的地球半径，h表示当地在电波射线轨迹上的海拔高度，h0表示雷达观测站的海拔高度，因此斯奈尔定律可写为：

n(a+h)cosθ＝n0(a+h0)cosθ0(6)

则：

将式(7)代入式(5)中，即可得到雷达的视在距离为：

地心张角与海拔高度h的关系为：

将上式左右两边同时进行积分，得：

其中，θ0表示雷达的视在仰角θ0，θ表示在海拔h处的射线的仰角；

根据三角形正弦定理知：

其中，α0表示目标的真实仰角，表示地心张角；

由式(11)可得目标的真实仰角α0为：

再次由正弦定理可知：

从而可推导出雷达观测站到目标的真实距离为：

已知雷达的视在距离re、视在仰角θ0，以及目标的真实仰角α0、真实距离r0，可以得出目标的距离的误差δr及仰角的误差ε，即：

以上，h为电波射线轨迹上某点的地面高度，是个变量，h0代表雷达观测站的海拔高度，hi是目标高度，hs为地面海拔高度，主要用于大气折射率指数模型，hk表示实测大气折射率剖面数据中的某个值。

下面以新乡地区为例对本发明的技术方案做一个具体的说明。利用该地区的一个五九型探空仪进行大气探测，试验中，目标是一个携带有gps的飞机，它能给出目标的真实位置，其飞行航线如图2所示，目标朝着雷达方向飞行，雷达测量的距离逐渐减小，仰角逐渐增大。

由图2可见，飞机几乎全程在9km高度处平飞状态，因此需要的大气折射率在10km高度以下范围有效，10km以上高度的大气折射率则对于本次试验中的折射误差计算不起作用。

将目标上带有的gps参数作为目标的真实位置，利用该目标真实位置和雷达的地理位置计算出雷达到目标的真实距离r0，将雷达实测的视在距离re减去相应的真实量，可得到电波折射引起的真实距离误差δr。

以下对本发明的计算精度进行验证，利用某地区的一个五九型探空仪进行大气探测，五九型探空仪的探测数据是不同高度对应的大气温度、气压和相对湿度等参数，再利用公式(24)、(25)计算不同高度对应的大气折射率，计算结果如图3所示。

式中，n为大气折射率；p为大气压强，hpa；t为空气热力学温度，k，t＝273+t,其中t为空气摄氏温度，℃；e为大气中水汽分压强，hpa。

式中，a、b、c分别为与空气温度有关的系数；rh为空气相对湿度(％)。

利用雷达对目标的实测视在距离re和视在仰角θ0，利用线性和分段两种插值方法获得的电波射线上的大气折射率进行折射误差计算，获得的距离折射误差分别为δr1和δr2，将两种计算出的折射误差减去图3中得到的真实误差δr，即可得到电波射线上大气折射率的不同插值方法对电波折射误差修正精度的影响，即δr1-δr和δr2-δr。

实验证明，在海拔3km左右，利用线性插值得到的折射率的误差率达到10％左右，对应的折射率为20左右，而采用分段插值得到的折射率的误差率只有6％左右，对应的折射率为12左右；在海拔大于十几公里以上时，分段插值获得大折射率几乎没有误差，而线性插值方法则有10％左右的误差，因此本发明能够降低大气折射率的误差，提高大气折射率的计算精度，从而提高雷达对目标的定位和测速精度。