适用于复杂飞行轨迹的双基聚束SAR大场景成像方法与流程

本发明属于雷达信号处理技术领域，具体涉及一种适用于复杂飞行轨迹的双基聚束sar大场景成像方法。

背景技术：

作为一种主动的航空、航天遥感手段，微波成像技术具有全天时、全天候工作的特点，在地质测绘、灾害监测、军事侦察等领域有着广泛的应用，目前已成为高分辨率对地观测和全球资源管理最重要手段之一。但是由于本身工作体制的限制，现有的合成孔径雷达(sar,syntheticapertureradar)并不能实现前视区域方位向高分辨成像，从而使sar在飞行器前视对地、自主着陆、物资空投、导弹末制导等方面不能充分的发挥作用。

双基地合成孔径雷达(bsar,bistaticsar)是一种sar体制推广到双基地雷达的微波成像技术，不仅具有几何构型灵活、隐蔽性强等优势，还能够克服单基地sar存在前视盲区的问题。在雷达平台运动过程中，发射站天线对成像区域进行照射、接收站天线接收成像区域中的目标散射回波；利用发射信号的大带宽形成距离向高分辨，通过成像处理算法补偿方位向信号的多普勒相位以实现方位向孔径合成进而形成方位向高分辨，从而实现成像区域内的两维高分辨成像。

目前的双基sar成像方法主要存在两方面缺陷。一方面，sar成像处理往往采用参考点目标的频谱函数(pointtargetreferencespectrum,ptrs)对回波信号进行一致压缩。而随着成像场景增大，场景中远处的目标回波的特性参数相对于参考点的差异增大，导致其方位向信号的相干叠加效果恶化，进而限制了双基地sar的有效成像场景尺寸。在大场景范围内实现高分辨雷达成像，可以让飞行器在战场侦察监视、物资空投和地震灾害救援等方面发挥更好的性能。文献“wu,j.,li,z.,huang,y.,yang,j.,&liu,q.h.ageneralizedomega-kalgorithmtoprocesstranslationallyvariantbistatic-sardatabasedontwo-dimensionalstoltmapping.ieeetransactionsongeoscience&remotesensing,52(10),6597-6614,2014”将回波信号频谱参数的空间变化规律近似建模为线性，一定程度上提高了一致聚焦的有效场景范围，但当场景尺寸进一步增大，线性近似仍然无法满足高精度成像的要求。另一方面，关于sar成像方法的理论研究往往将雷达平台的飞行建模为匀速直线运动，而实际工作中平台飞行往往存在一定的机动，运动轨迹的高阶分量将带来显著的相位误差，进一步限制有效的成像场景尺寸。目前关于双基聚束sar成像方法的研究结果中，还没有一种方法能够在保证算法效率的前提下，同时解决复杂飞行轨迹和大场景一致聚焦两大问题。

技术实现要素：

本发明的发明目的是：为了解决现有技术在双基地聚束sar成像处理中的缺陷，本发明提出了一种适用于复杂飞行轨迹的双基聚束sar大场景成像方法。

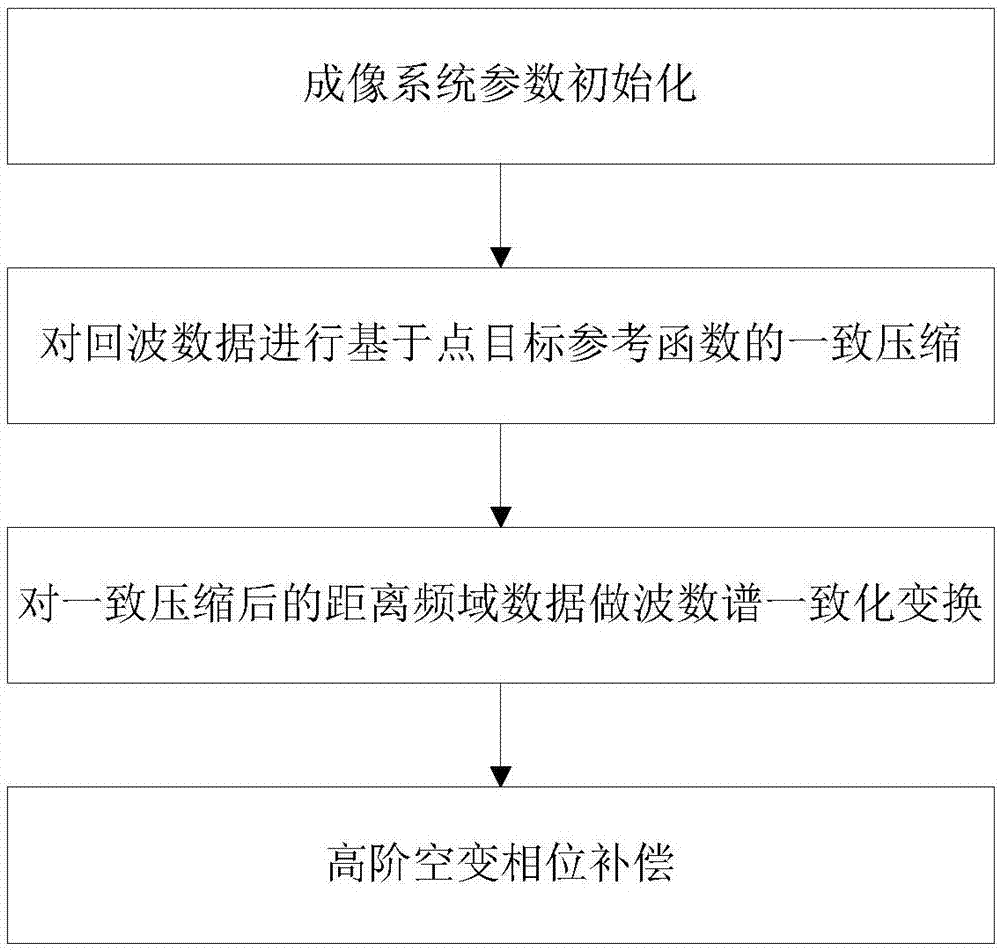
本发明的技术方案是：一种适用于复杂飞行轨迹的双基聚束sar大场景成像方法，包括以下步骤：

a、成像系统参数初始化

所述成像系统参数包括参考点位置、发射站三维轨迹[xt(t),yt(t),zt(t)]、接收站三维轨迹[xr(t),yr(t),zr(t)]、发射信号载波频率fc、脉冲宽度tp、距离向采样频率fs、距离向采样点数nr、脉冲重复间隔pri、方位时间向量t、距离时间向量τ、距离频率向量fτ、场景中点目标(xp,yp)的距离历史rb(t；xp,yp)；

b、对回波数据进行基于点目标参考函数的一致压缩

根据参考点目标的回波数据构造点目标参考函数，利用距离频域和方位时域对回波数据进行一致压缩，得到一致压缩后的距离频域数据；

c、对一致压缩后的距离频域数据做波数谱一致化变换

将差分距离史对空间坐标二维泰勒展开，根据双平台轨迹信息构造映射关系，通过二维插值将一致压缩后的数据变换到二维波数域，得到波数谱一致化的数据；

d、高阶空变相位补偿

将粗成像结果划分为多个子图像，构造空变相位补偿因子，计算每个子图像对应的相位补偿因子并进行相位补偿，将所有相位补偿后的子图像进行拼接得到成像结果。

进一步地，所述步骤b中，点目标参考函数表示为

其中，so(fτ,t)表示点目标参考函数，kr为发射信号调频率，c为光速。

进一步地，所述步骤b中，利用距离频域、方位时域的共轭相乘，对回波数据进行一致压缩，一致压缩后的距离频域数据表示为

其中，fftr{·}表示距离向fft，sr(τ,t；xp,yp)表示目标回波数据，so^*(fτ,t)表示对一致压缩参考信号so(fτ,t)取共轭，δrp(t；xp,yp)表示差分距离史，wr[·]表示距离向时域窗函数，wa[·]表示方位向时域窗函数，ta表示合成孔径时间。

进一步地，所述步骤c中，将差分距离史对空间坐标二维泰勒展开，表示为

其中，rcur(t,xp,yp)表示距离误差。

进一步地，所述步骤d中，首先计算补偿前的有效场景尺寸，计算公式为

其中，qi和ti均为雷达平台运动轨迹相关系数，λ表示载波波长；

再根据有效场景尺寸将粗成像结果hcur(x,y)划分为多个子图像hi(x,y)。

进一步地，所述步骤d中，构造空变相位补偿因子，表示为

hc(kx,ky；xp,yp)＝exp{jkr(kx,ky)rcur[t(kx,ky)；xp,yp]}

其中，kx和ky分别为x和y方向上的波数，kr(kx,ky)表示由kx和ky来表示kr的二维函数映射，t(kx,ky)表示由kx和ky来表示t的二维函数映射。

进一步地，所述步骤d中，对每个子图像hi(x,y)，先确定其几何中心位置(xi,yi)，将子图像进行二维快速傅里叶变换，得到其波数谱hi(kx,ky)；再计算出对应的相位补偿因子hc(kx,ky；xi,yi)，与子图像波数谱相乘后再求解乘积结果的二维逆向快速傅里叶变换，得到补偿后的子图像。

进一步地，所述步骤d中，补偿后的子图像表示为

hi′(x,y)＝ifft2{fft2{hi(x,y)}·hc(kx,ky；xi,yi)}。

本发明的有益效果是：本发明采用基于线性空变假设的波数谱一致化方法实现复杂飞行轨迹下的sar回波一致聚焦，并通过高阶空变相位补偿提高有效聚焦景深，通过这两种处理技术的结合实现了复杂飞行轨迹下的双基sar大场景成像处理；本发明不仅克服了现有sar成像算法对复杂轨迹适应性差的缺陷，而且能够以高的运算效率实现聚束模式的大场景高分辨率一致聚焦，可以在较大的成像场景范围内，实现高分辨率的成像处理，使搭载双基sar系统的飞行器在战场侦察监视、物资空投和地震灾害救援等领域发挥更好的性能。

附图说明

图1是本发明的适用于复杂飞行轨迹的双基聚束sar大场景成像方法的流程示意图；

图2是本发明实施例中采用的双基sar成像系统几何示意图；

图3是本发明实施例中采用的目标场景布置图；

图4是本发明实施例中对目标场景的成像仿真结果示意图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。

为了方便描述本发明的内容，首先对以下术语进行解释：

术语1：双基地合成孔径雷达(bistaticsyntheticapertureradar,bisar)

双基地合成孔径雷达是指在雷达平台运动过程中，发射站天线对成像区域进行照射、接收站天线接收成像区域中的目标散射回波；利用发射信号的大带宽形成距离向高分辨，通过成像处理算法补偿方位向信号的多普勒相位以实现方位向孔径合成进而形成方位向高分辨，从而实现成像区域内的两维高分辨成像。

术语2：点目标参考函数(pointtargetreferencefunction)

点目标参考函数是指对回波数据进行一致压缩时采用的参考点的信号函数。参考函数可以是时域的，也可以是频域的，如在某个域生成了参考函数，成像处理时则将回波信号与参考函数在该域上共轭相乘，再变换到时频对应的另一个域上实现压缩。参考函数一般只包含相位项，不包含包络项。

术语3：有效成像场景尺寸

有效场景尺寸是指对某个特定的成像方法，在保证场景内所有位置目标回波的聚焦效果良好时可以允许的最大成像场景两维尺寸。sar成像处理中，聚焦效果一般在场景边缘最差，散焦效应往往由在成像方法中被忽略的方位时间的二次相位误差(quadraticphaseerror,qpe)导致，因此有效场景尺寸一般可以通过对qpe的数值加以限制来求出。

如图1所示，为本发明的适用于复杂飞行轨迹的双基聚束sar大场景成像方法的流程示意图。一种适用于复杂飞行轨迹的双基聚束sar大场景成像方法，包括以下步骤：

a、成像系统参数初始化

所述成像系统参数包括参考点位置、发射站三维轨迹[xt(t),yt(t),zt(t)]、接收站三维轨迹[xr(t),yr(t),zr(t)]、发射信号载波频率fc、脉冲宽度tp、距离向采样频率fs、距离向采样点数nr、脉冲重复间隔pri、方位时间向量t、距离时间向量τ、距离频率向量fτ、场景中点目标(xp,yp)的距离历史rb(t；xp,yp)；

b、对回波数据进行基于点目标参考函数的一致压缩

根据参考点目标的回波数据构造点目标参考函数，利用距离频域和方位时域对回波数据进行一致压缩，得到一致压缩后的距离频域数据；

c、对一致压缩后的距离频域数据做波数谱一致化变换

将差分距离史对空间坐标二维泰勒展开，根据双平台轨迹信息构造映射关系，通过二维插值将一致压缩后的数据变换到二维波数域，得到波数谱一致化的数据；

d、高阶空变相位补偿

将粗成像结果划分为多个子图像，构造空变相位补偿因子，计算每个子图像对应的相位补偿因子并进行相位补偿，将所有相位补偿后的子图像进行拼接得到成像结果。

在本发明的一个可选实施例中，上述步骤a初始化成像系统参数，包括参考点位置，定义为(0,0,0)；发射站三维轨迹，记为[xt(t),yt(t),zt(t)]；接收站三维轨迹，记为[xr(t),yr(t),zr(t)]；发射信号载波频率，记为fc；脉冲宽度，记为tp；距离向采样频率，记为fs；距离向采样点数，记为nr；脉冲重复间隔，记为pri；方位时间向量，记为t＝[-pri·na/2,-pri·(na/2-1),···,pri·(na/2-1)]，距离时间向量，记为τ＝[-1/fs·nr/2,-1/fs·(nr/2-1),···,1/fs·(nr/2-1)]；距离频率向量，记为fτ＝[-fs/2,-fs·(nr/2-1)/nr,···,fs·(nr/2-1)/nr]；

场景中点目标(xp,yp)的距离历史为：

rb(t；xp,yp)＝rt(t；xp,yp)+rr(t；xp,yp)

其中，rt(t；xp,yp)表示发射站(t)的距离历史，表示发射站(t)的轨迹矢量，rr(t；xp,yp)表示接收站(r)的距离历史，表示接收站(r)的轨迹矢量。

如图2所示，为本发明实施例中采用的双基sar成像系统几何示意图。系统坐标系以雷达双站波束中心所指的地表点为坐标原点，平台沿弯曲轨迹运动。成像系统参数如表1所示。

表1、成像系统参数

如图3所示，为本发明实施例中采用的目标场景布置图；图中的圆点为布置于地面上7×7共49个点目标。这49个点沿x和y方向的间隔均为400m。场景中任一点的位置坐标记为p(x,y)。

构造方位时间向量t＝[-pri·na/2,-pri·(na/2-1),···,pri·(na/2-1)]，其中，pri为脉冲重复时间，na为目标回波方位向采样点数。距离时间向量，记为τ＝[-1/fs·nr/2,-1/fs·(nr/2-1),···,1/fs·(nr/2-1)]，其中，fs为距离向采样率，nr为目标回波距离向采样点数。

在本发明的一个可选实施例中，上述步骤b按照步骤a中初始化的雷达平台飞行轨迹和点目标坐标位置，利用matlab仿真出点目标回波数据sr(τ,t；xp,yp)，表示为

其中，σp(xp,yp)表示目标散射截面积(rcs)；wr[·]表示距离向时域窗函数，代表发射脉冲信号的包络，窗宽度为tp；wa[·]表示方位向时域窗函数，代表天线方向图的调制效应，窗宽度为合成孔径时间ta；kr为发射信号调频率；c为光速；λ为载波波长。

根据参考点目标的回波数据，构造一致压缩参考信号，表示为

其中，so(fτ,t)表示点目标参考函数，so*(fτ,t)表示对一致压缩参考信号so(fτ,t)取共轭，δrp(t；xp,yp)表示差分距离史，。

再利用距离频域和方位时域将回波信号与参考信号进行共轭点乘，对回波数据进行一致压缩，压缩后的距离频域数据表示为：

其中，fftr{·}表示距离向fft，so*(fτ,t)表示对一致压缩参考信号so(fτ,t)取共轭，

其中，下角标0表示点目标位于中心点，δ表示差分，δrt(t；xp,yp)表示发射站差分距离历史，δrr(t；xp,yp)表示接收站的差分距离历史。

在本发明的一个可选实施例中，上述步骤c将差分距离史δrb(t；xp,yp)对空间坐标(xp,yp)二维泰勒展开并将展开式分成线性项及高阶项，可以得到：

其中rt(t)＝||rt(t)||2，rr(t)＝||rr(t)||2；δrcur(t,xp,yp)一般保留至三阶，即：

再利用平台轨迹数据构造映射关系

其中，kx和ky分别为x和y方向上的波数。

根据映射关系，通过二维插值将一致压缩后的数据sd(fτ,t；xp,yp)变换到由kx,ky定义的二维波数域，得到波数谱一致化的数据，表示为

其中，wk(kx,ky)为经上述二维变换后的波数谱包络；为经二维变换后的波数域高阶空变相位；数据映射后的二维波数kx,ky分别为

其中，kxmin,kymin分别为x方向波数和y方向波数的最小值，kxmax,kymax分别为x方向波数和y方向波数的最大值，均可根据上文给出的波数映射关系求出；dx,dy分别为成像场景的x方向尺寸和y方向尺寸。

将整个场景中所有目标的回波信号进行处理后的的结果为

然后对该结果做二维逆向快速傅里叶变换，得到波数谱一致化的粗成像结果hcur(x,y)。

在本发明的一个可选实施例中，上述步骤d首先计算补偿前的有效场景尺寸，计算公式为

其中，qi和ti均为雷达平台运动轨迹相关系数，表示为：

求得关于xp和yp的取值范围后，将粗成像结果hcur(x,y)划分为若干尺寸由该取值范围确定的子图像hi(x,y)。

然后，根据每一个子图像的中心位置(xi,yi)构造空变相位补偿因子，表示为

hc(kx,ky；xp,yp)＝exp{jkr(kx,ky)rcur[t(kx,ky)；xp,yp]}

其中，kx和ky分别为x和y方向上的波数，kr(kx,ky)表示由kx和ky来表示kr的二维函数映射，t(kx,ky)表示由kx和ky来表示t的二维函数映射，rcur表示距离误差。

t(kx,ky)定义为如下方程的解：

令系数a0,a1,a2,a3,...的求取公式为

a0＝f(0)

a1＝f'(0)

利用平台轨迹数据计算出上述数据向量并进行多项式拟合，得到系数a0,a1,a2,a3,...的值，再通过级数反演得到：

而kr(kx,ky)定义为：

对每个子图像hi(x,y)，先确定其几何中心位置(xi,yi)，将子图像进行二维快速傅里叶变换，得到其波数谱hi(kx,ky)；再计算出对应的相位补偿因子hc(kx,ky；xi,yi)，与子图像波数谱相乘后再求解乘积结果的二维逆向快速傅里叶变换，得到补偿后的子图像，表示为

hi′(x,y)＝ifft2{fft2{hi(x,y)}·hc(kx,ky；xi,yi)}。

所有子图像完成相位补偿后，将所有相位补偿后的子图像按照几何关系进行图像拼接，得到大场景一致聚焦的成像结果h′(x,y)。

如图4所示，为本发明实施例中对目标场景的成像仿真结果示意图；可以看出，本发明在较大的成像场景范围内，实现了高分辨率一致聚焦的成像处理。

本领域的普通技术人员将会意识到，这里所述的实施例是为了帮助读者理解本发明的原理，应被理解为本发明的保护范围并不局限于这样的特别陈述和实施例。本领域的普通技术人员可以根据本发明公开的这些技术启示做出各种不脱离本发明实质的其它各种具体变形和组合，这些变形和组合仍然在本发明的保护范围内。