一种基于块稀疏贝叶斯模型的辐射源直接定位方法与流程

本发明涉及一种基于块稀疏贝叶斯模型的辐射源直接定位方法，属于辐射源定位技术领域。

背景技术：

辐射源定位技术在雷达、声呐和无线通信领域都是一个重要的研究课题。传统的基于到达角度的辐射源定位方法包括两个步骤：到达角估计以及和目标位置解算，因此各基站之间的数据关联不可或缺。不同于传统的间接定位方法，直接定位方法能够利用阵列接收数据直接得到目标位置的估计结果，避免了数据关联中可能带来的测量值配对错误。然而，上述两类定位方法均需已知目标个数，且在低信噪比和小快拍情形下定位性能急剧下降。

技术实现要素：

本发明为了解决现有定位方法需要已知目标个数，并且在低信噪比和小快拍情形下定位性能急剧下降的问题，提出了一种基于块稀疏贝叶斯模型的辐射源直接定位方法，该方法能在未知目标个数的情形下对辐射源进行定位，并获得更好的定位性能。该方法适用于辐射源信号对于每个基站呈窄带特性而在基站之间呈宽带特性的条件下，且在处理过程中仅利用到了信号的波达角度信息，对各个基站的无接收同步要求。本发明所述一种基于块稀疏贝叶斯模型的辐射源直接定位方法采取的技术方案如下：

一种基于块稀疏贝叶斯模型的辐射源直接定位方法，所述辐射源直接定位方法包括：

步骤一：针对在平面内的l个分立的基站和n个窄带辐射源，在辐射源信号对于每个基站呈窄带特性而在基站之间呈宽带特性的条件下对第l个基站的接收数据建模，其中每个基站线性配置m个传感器，并有m≥2，l≥2，1≤n≤m-1；而后将所述接收模型进行块稀疏贝叶斯扩展，获得所述接收数据的块稀疏模型；

步骤二：根据信号的高斯统计特性得到信号统计参量的后验更新；

步骤三：利用边缘概率密度积分获得最大似然意义下的参数估计代价函数；利用期望最大原理获取所述参数估计代价函数的上界函数，而后分别针对噪声功率和块内相关度参数对上界函数进行求导，对应获取使上界函数最小的噪声功率和块内相关度参数的更新表达式；依据泰勒展开原理及恒等变换获得所述参数估计代价函数的另一上界函数，而后针对块间稀疏性参数对该上界函数求导，获得使上界函数最小的块间稀疏性参数的更新表达式；

步骤四：重复步骤二与步骤三所述过程，直至参数估计代价函数最终收敛；根据信号后验均值参量的峰值位置确定辐射源的位置。

进一步地，步骤一所述接收数据的块稀疏模型的建立过程包括：

第一步：在平面内设置l个分立的基站，每个基站线性配置m个传感器和n个窄带辐射源，其中，m≥2，l≥2，1≤n≤m-1；发射信号表示为：sn(t)(1≤n≤n)，n代表信号编号索引；辐射源位置坐标由位置矢量pn(1≤n≤n)确定；利用l代表基站编号索引，则第l个基站的接收数据表示为：

其中，

其中，wl,n为一未知复参量，代表从第n个辐射源到第l个基站的信道衰落；高斯分布的随机矢量nl(t)表示阵列噪声；al(pn)为阵列导向矢量，τl(pn)为信号的传播延迟，ψl(pn)为信号在两相邻传感器之间的相位延迟；

在辐射源信号对于每个基站呈窄带特性而在基站之间呈宽带特性的条件下，将来自同一辐射源而被不同基站接收的信号建模为相互独立的不同信号，确定接收模型为：

x(t)＝φ^ss^s(t)+n(t)

其中，

其中，上标(·)^s代表基站建模参数；φ^s代表总导向矩阵；代表第n个辐射源的导向矩阵；sl,n(t)代表第l个基站接收到的第n个信号；

第二步：将所述接收模型进行块稀疏贝叶斯扩展，获得所述接收数据的块稀疏模型，所述接收数据的块稀疏模型如下：

其中，

其中，q代表稀疏字典的原子个数；上划线代表稀疏框架下的模型参数；代表块稀疏字典；代表字典中第q个块；代表信号的概率密度函数；代表均值为零向量，协方差矩阵为的高斯分布，γq为表征块间稀疏性的参数，为表征块内相关度的参数。

进一步地，步骤二所述信号统计参量的后验更新包括：

根据信号的高斯统计特性：

其中，

γ＝[γ1,γ2,...,γq]^t

得到信号统计参量的后验更新表达式为：

其中，

其中，λ代表噪声功率；代表信号的后验均值；代表信号的后验协方差矩阵；代表信号的先验协方差矩阵；i代表单位阵。

进一步地，步骤三所述模型参数解算过程包括：

第一步：利用边缘概率密度积分获得最大似然意义下的参数估计代价函数，所述参数估计代价函数为：

其中，t代表采样快拍数；表示未知参数集；

第二步：根据期望最大理论，确定所述参数估计代价函数的上界函数，所述参数估计代价函数的上界函数为：

其中，上标θ^(old)代表上一次更新的参数取值；

第三步：通过求导确定使上界函数最小的λ的更新表达式，所述使上界函数最小的λ的更新表达式为：

第四步：通过求导方式获得的更新表达式，所述的更新表达式如下：

其中，代表的第q个块，代表对角线上的第q个块矩阵；

第五步：根据参数估计代价函数中的第一项式进行泰勒展开，获得第一项泰勒展开式为：

其中，代表的第q列，q为稀疏字典的原子索引；代表的上一次更新值；代表γq的上一次更新值；

第六步：将参数估计代价函数中的第二项式进行恒等变换，获得第二项的恒等变换式为：

第七步：根据步骤三第五步、第六步确定另一上界函数所述另一上界函数的表达式为：

第八步：参数γ的更新表达式通过对求导得到，参数γ第q个元素的表达式为：

本发明有益效果：

本发明提出的一种基于块稀疏贝叶斯模型的辐射源直接定位方法的代价函数是基于块稀疏贝叶斯模型给出的，该方法无需已知目标个数也无需人工整定超参数；相比于传统方法，本发明所提方法具有更高的定位性能且无需数据关联。

附图说明

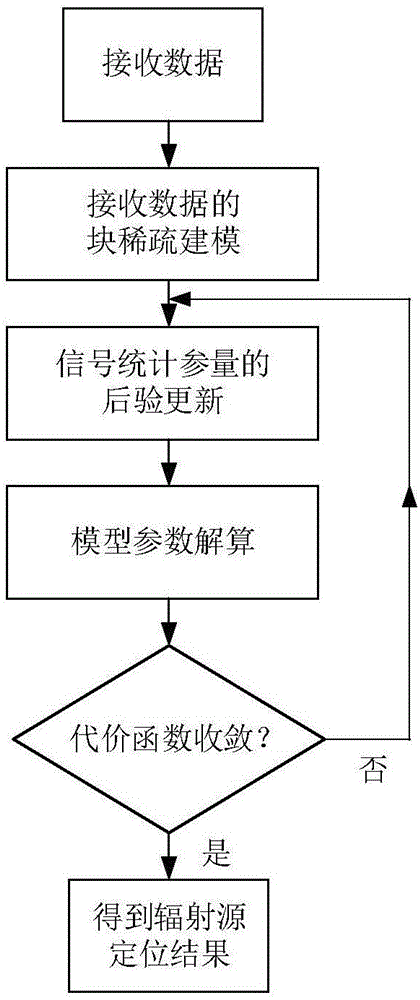
图1为本发明所提方法流程图。

图2为辐射源定位系统示意图。

图3为定位性能仿真结果。

具体实施方式

下面结合具体实施例对本发明做进一步说明，但本发明不受实施例的限制。

实施例1：

一种基于块稀疏贝叶斯模型的辐射源直接定位方法，如图1所示，所述辐射源直接定位方法包括：

步骤一：针对在平面内的l个分立的基站和n个窄带辐射源，在辐射源信号对于每个基站呈窄带特性而在基站之间呈宽带特性的条件下对第l个基站的接收数据建模，其中每个基站线性配置m个传感器，并有m≥2，l≥2，1≤n≤m-1；而后将所述接收模型进行块稀疏贝叶斯扩展，获得所述接收数据的块稀疏模型；

步骤二：根据信号的高斯统计特性得到信号统计参量的后验更新；

步骤三：利用边缘概率密度积分获得最大似然意义下的参数估计代价函数；利用期望最大原理获取所述参数估计代价函数的上界函数，而后分别针对噪声功率和块内相关度参数对上界函数进行求导，对应获取使上界函数最小的噪声功率和块内相关度参数的更新表达式；依据泰勒展开原理及恒等变换获得所述参数估计代价函数的另一上界函数，而后针对块间稀疏性参数对该上界函数求导，获得使上界函数最小的块间稀疏性参数的更新表达式；

步骤四：重复步骤二与步骤三所述过程，直至参数估计代价函数最终收敛；根据信号后验均值参量的峰值位置确定辐射源的位置。

为方便表述与理解，将如下所用符号统一说明：矩阵与矢量以粗斜体符号表示；上标(·)^t、(·)^h和(·)^-1分别表示转置、共轭转置和取逆操作符；符号|·|，||·||，tr(·)和diag(·)分别表示取行列式，取2范数、取迹和对角化操作；

其中，步骤一所述接收数据的块稀疏模型的建立过程包括：

第一步：如图2所示，在平面内设置l个分立的基站，每个基站线性配置m个传感器和n个窄带辐射源，其中，m≥2，l≥2，1≤n≤m-1；发射信号表示为：sn(t)(1≤n≤n)，n代表信号编号索引；辐射源位置坐标由位置矢量pn(1≤n≤n)确定；利用l代表基站编号索引，则第l个基站的接收数据表示为：

其中，

其中，wl,n为一未知复参量，代表从第n个辐射源到第l个基站的信道衰落；高斯分布的随机矢量nl(t)表示阵列噪声；al(pn)为阵列导向矢量，τl(pn)为信号的传播延迟，ψl(pn)为信号在两相邻传感器之间的相位延迟；

在辐射源信号对于每个基站呈窄带特性而在基站之间呈宽带特性的条件下，将来自同一辐射源而被不同基站接收的信号建模为相互独立的不同信号，确定接收模型为：

x(t)＝φ^ss^s(t)+n(t)

其中，

其中，上标(·)^s代表基站建模参数；φ^s代表总导向矩阵；代表第n个辐射源的导向矩阵；sl,n(t)代表第l个基站接收到的第n个信号；

第二步：将所述接收模型进行块稀疏贝叶斯扩展，获得所述接收数据的块稀疏模型，所述接收数据的块稀疏模型如下：

其中，

其中，q代表稀疏字典的原子个数；上划线代表稀疏框架下的模型参数；代表块稀疏字典；代表字典中第q个块；代表信号的概率密度函数；代表均值为零向量，协方差矩阵为的高斯分布，γq为表征块间稀疏性的参数，为表征块内相关度的参数。

步骤二所述信号统计参量的后验更新包括：

根据信号的高斯统计特性：

其中，

γ＝[γ1,γ2,...,γq]^t

得到信号统计参量的后验更新表达式为：

其中，

其中，λ代表噪声功率；代表信号的后验均值；代表信号的后验协方差矩阵；代表信号的先验协方差矩阵；i代表单位阵。

步骤三所述模型参数解算过程包括：

第一步：利用边缘概率密度积分获得最大似然意义下的参数估计代价函数，所述参数估计代价函数为：

其中，t代表采样快拍数；表示未知参数集；

第二步：根据期望最大理论，确定所述参数估计代价函数的上界函数，所述参数估计代价函数的上界函数为：

其中，上标θ^(old)代表上一次更新的参数取值；

第三步：通过求导确定使上界函数最小的λ的更新表达式，所述使上界函数最小的λ的更新表达式为：

第四步：通过求导方式获得的更新表达式，所述的更新表达式如下：

其中，代表的第q个块，代表对角线上的第q个块矩阵；

第五步：根据参数估计代价函数中的第一项式进行泰勒展开，获得第一项泰勒展开式为：

其中，代表的第q列，q为稀疏字典的原子索引；代表的上一次更新值；代表γq的上一次更新值；

第六步：将参数估计代价函数中的第二项式进行恒等变换，获得第二项的恒等变换式为：

第七步：根据步骤三第五步、第六步确定另一上界函数所述另一上界函数的表达式为：

第八步：参数γ的更新表达式通过对求导得到，参数γ第q个元素的表达式为：

所提一种基于块稀疏贝叶斯模型的辐射源直接定位方法适用于辐射源信号对于每个基站呈窄带特性而在基站之间呈宽带特性的条件下，且在处理过程中仅利用到了信号的波达角度信息，对各个基站的无接收同步要求。

利用所提一种基于块稀疏贝叶斯模型的辐射源直接定位方法得到的定位结果均方误差曲线如图3所示，其仿真条件如下：辐射源位置位于(0,-0.5)和(0,0.5)km处，基站位于(-3,-3)、(-3,3)、(3,-3)和(3,3)km处。阵元间距为半波长，接收信噪比为20db；信号到各站的衰减因子分别设置为：w1＝[1.1,0.5]，w2＝[1.5,1.3]，w3＝[0.8,0.7]和w4＝[0.4,1.6]；入射信号由1000个具有随机幅度和相位的单频信号叠加而成，其频率在带宽范围内随机生成；取10个观测快拍给出仿真，变化信噪比从0db至25db；根据仿真结果，本发明所提方法的定位均方误差优于现有的直接定位方法。

虽然本发明已以较佳的实施例公开如上，但其并非用以限定本发明，任何熟悉此技术的人，在不脱离本发明的精神和范围内，都可以做各种改动和修饰，因此本发明的保护范围应该以权利要求书所界定的为准。