基于故障前后电压、电流变化的输电线路故障定位方法与流程

本发明涉及一种基于故障前后电压、电流变化的输电线路故障定位方法。

背景技术：

输电线路作为整个电网的核心组成部分，一旦发生故障，就会造成电力输送的中断，将会严重影响人们正常的生产、生活。对于远距离输电线路，很难在发生故障后通过人工巡线查找、清除故障，因此一种准确、迅速的故障定位方法对于减少经济损失、提高系统稳定性具有重要意义。

目前，常见的输电线路故障定位方法可划分为行波法和阻抗法两大类。行波法通过检测故障行波的波头信息进行故障定位，对行波检测装置的采样频率要求非常高，很难在实际电网中大规模应用。阻抗法通过推导包含故障距离、系统参数的关系式进行求解，计算故障位置，方法简单，定位迅速，能应用于多种类型故障的定位，另外，利用两端的同步数据也可以消除故障电阻的影响，在故障定位领域有很高的应用价值。因此研究原理简单、实用性强、可靠性高的新型输电线路故障定位方法具有重要的现实意义。

技术实现要素：

本发明的目的是针对现有技术存在的问题，提供一种基于故障前后电压、电流变化的输电线路故障定位方法，能够更方便、快速地实现输电线路故障定位。

为实现上述目的，本发明采用的技术方案为：

基于故障前后电压、电流变化的输电线路故障定位方法，包括如下步骤：

步骤1、建立输电线路分布参数模型，计算线路的传播系数γ和特征阻抗z，推导包含故障距离、传播系数、特征阻抗和双端电气量的故障定位方程；

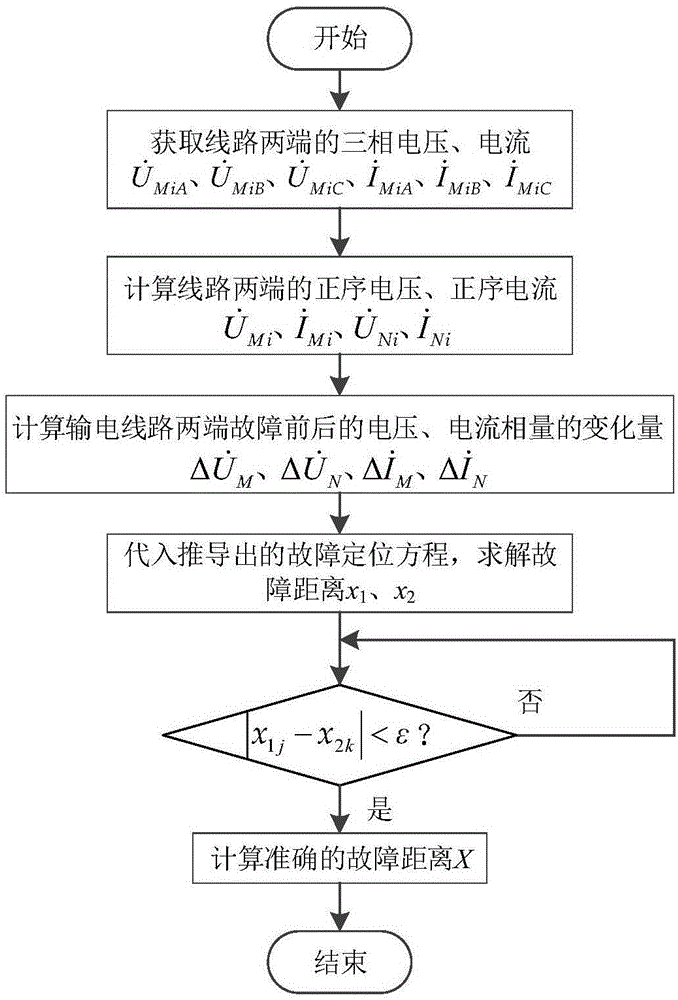
步骤2、在输电线路上检测到故障后，分别提取线路两端安装的pmu记录的三相电压、电流数据和其中，i＝1，2，分别代表故障前和故障后，m代表线路首端，n代表线路末端，a、b、c分别代表a相、b相、c相；

步骤3、根据步骤2的数据，计算线路两端的正序电压和正序电流的值；

步骤4、利用式(1)计算输电线路两端故障前后的电压、电流相量的变化量：

其中，代表线路首端、末端电压相量的变化量，代表线路首端、末端电流相量的变化量；

步骤5、将步骤4中的计算结果代入步骤1中推导出的故障定位方程，求解故障距离x1、x2，如式(2)所示，

re(a)x1²+re(b)x1+re(c)＝0

im(a)x2²+im(b)x2+im(c)＝0(2)

其中，x1、x2代表故障点与线路首端m之间的距离，re和im分别代表实部和虚部，且

这里，l代表输电线路的长度；

步骤6、将步骤5求解出的初步故障距离代入式(3)，选择正确的故障距离xre和xim：

|x1j-x2k|＜ε(3)

其中，x1j代表求解步骤5中实部方程得到的j个解，x2k代表求解步骤5中虚部方程得到的k个解，xre代表由实部方程得到的正确故障距离，xim代表由虚部方程得到的正确故障距离，ε代表选择阈值；

步骤7、根据步骤6中的选择，利用式(4)计算准确的故障距离x：

优选地，步骤1中，计算线路的传播系数γ和特征阻抗z的步骤进一步包括：

其中，z0代表单位长度线路的阻抗，y0代表单位长度线路的导纳。

优选地，步骤1中，推导包含故障距离、传播系数、特征阻抗和双端电气量的故障定位方程的步骤进一步包括：

①对于输电线路，从线路两端计算任意一点的电压相量的公式为：

②当故障发生后，利用式(6)从线路两端推算故障点的正序电压

其中，l代表输电线路的长度；

由于从线路两端推算出的故障点电压uf值相等，得到：

③同样，在未发生故障时，对于位置x，依然满足从线路两端推算至x处的电压相等，得到：

二者形式相同，参数一致，将式(8)和式(9)相减得到：

④为了简化计算，将cosh(x)和sinh(x)泰勒展开，分别取前两项和第一项：

sinh(x)＝x

cosh(x)＝1+x²(11)

将化简后的双曲正弦、余弦函数代入式(10)，整理成一元二次方程的标准形式，分别取系数a、b、c的实部和虚部即可得到故障定位方程：

re(a)x²+re(b)x+re(c)＝0

im(a)x²+im(b)x+im(c)＝0(12)

其中，x代表故障点与线路首端m之间的距离，re和im分别代表实部和虚部，且

优选地，步骤3中，计算线路两端的正序电压、正序电流的步骤进一步包括：

其中，a代表运算算子，a＝e^j120°。

优选地，步骤6中，实部方程得到的解的个数j＝2，虚部方程得到的解的个数k＝2。

优选地，步骤6中，在故障距离选择时，ε的值取为2km。

与现有技术相比，本发明的有益效果是：本发明不受过渡电阻与故障初始角的影响，适用于输电线路上各种类型的短路和接地故障，在发生近母线故障时也能有效确定故障位置，具有较高的精度、可靠性和工程实践意义。

附图说明

图1为本发明中基于故障前后电压、电流变化的输电线路故障定位方法的流程图；

图2为本发明输电线路分布参数模型的示意图；

图3为根据实施例的本发明输电线路结构示意图。

具体实施方式

下面将结合本发明中的附图，对本发明的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动条件下所获得的所有其它实施例，都属于本发明保护的范围。

如图1所示，本发明提出了一种基于故障前后电压、电流变化的输电线路故障定位方法，包括如下步骤：

步骤1、建立如图2所示的输电线路分布参数模型，计算线路的传播系数γ和特征阻抗z，推导包含故障距离、传播系数、特征阻抗和双端电气量的故障定位方程。

具体如下：

①根据输电线路分布参数模型，计算输电线路的传播系数γ和特征阻抗z：

其中，z0代表单位长度线路的阻抗，y0代表单位长度线路的导纳。

②基于输电线路的分布参数模型，可以推导出从线路两端计算任意一点的电压相量值的公式为：

其中，m代表线路首端，n代表线路末端，l代表输电线路的长度。

③当故障发生后，利用式(6)从线路两端推算故障点的正序电压

其中，下标2代表故障发生后。

由于从线路两端推算出的故障点电压uf值相等，可得：

④同样，在未发生故障时，对于位置x，依然满足从线路两端推算至x处的电压相等，可得：

其中，下标1代表故障发生前。

式(8)和式(9)的形式相同，参数一致，将这两个式子相减可得：

其中，代表线路首端、末端电压相量的变化量，代表线路首端、末端电流相量的变化量。

⑤为了简化计算，将cosh(x)和sinh(x)泰勒展开，分别取前两项和第一项：

sinh(x)＝x

cosh(x)＝1+x²(11)

将化简后的双曲正弦、余弦函数代入式(10)，整理成一元二次方程的标准形式，分别取系数a、b、c的实部和虚部即可得到故障定位方程：

re(a)x²+re(b)x+re(c)＝0

im(a)x²+im(b)x+im(c)＝0(12)

其中，x代表故障点与线路首端m之间的距离，re和im分别代表实部和虚部，且

(2)在输电线路上检测到故障后，分别提取线路两端安装的pmu(phasormeasurementunit，相量测量单元)记录的三相电压、电流数据和

其中，i＝1、2，分别代表故障前和故障后，a、b、c分别代表a相、b相、c相。

(3)根据步骤2的数据，计算线路两端的正序电压和正序电流的值。

其中，a代表运算算子，a＝e^j120°。

(4)利用式(1)计算输电线路两端故障前后的电压、电流相量的变化量：

其中，代表线路首端、末端电压相量的变化量，代表线路首端、末端电流相量的变化量。

(5)将步骤4中的计算结果代入故障定位方程，求解故障距离x1、x2。

re(a)·x1²+re(b)·x1+re(c)＝0

im(a)·x2²+im(b)·x2+im(c)＝0(2)

其中，x1、x2代表故障点与线路首端m之间的距离，re和im分别代表实部和虚部，且

这里，l代表输电线路的长度。

(6)将步骤5求解出的初步故障距离代入式(3)，选择正确的故障距离xre和xim：

|x1j-x2k|＜ε(3)

其中，x1j代表求解步骤5中实部方程得到的j个解，j＝2，x2k代表求解步骤5中虚部方程得到的k个解，k＝2，xre代表由实部方程得到的正确故障距离，xim代表由虚部方程得到的正确故障距离，ε代表选择阈值，ε＝2km。

步骤7、根据步骤6中的选择，利用式(4)计算准确的故障距离x：

实施例

在pscad/emtdc上搭建双端输电线路模型，如图3所示。输电线路的不同位置上模拟了具有不同故障电阻(10ω和200ω)和不同故障类型(单相接地和两相短路)的故障，线路全长为250km。采用本发明提出的输电线路故障定位方法，得到的故障定位结果如表1所示。表1中，故障距离指的是故障点与线路首端m之间的距离，xre指的是实部方程求解出的故障距离，xim指的是虚部方程求解出的故障距离，故障定位误差e由下式定义：

式(14)中，x为求解出的故障距离，xr为真正的故障距离，l为输电线路的长度。从表1中可以看出，故障定位误差不受故障电阻和故障类型的影响，在各种情况下定位误差均小于1km。

表1不同故障电阻和故障类型下的定位结果

本发明公开了一种基于故障前后电压、电流变化的输电线路故障定位方法。首先根据输电线路的分布参数模型构建故障定位方程，在故障发生后，利用输电线路两端pmu记录下的电压、电流相量值计算故障前后的正序电压、正序电流变化量，代入构造的故障定位方程，计算故障位置。本发明不受过渡电阻与故障初始角的影响，适用于各种类型的短路和接地故障，在发生近母线故障时也能有效确定故障位置，具有较高的精度、可靠性和工程实践意义。

尽管已经示出和描述了本发明的实施例，对于本领域的普通技术人员而言，可以理解在不脱离本发明的原理和精神的情况下可以对这些实施例进行多种变化、修改、替换和变型，本发明的范围由所附权利要求及其等同物限定。