一种基于包络校正的方位NCS成像方法、系统、介质及设备与流程

本发明涉及合成孔径雷达方位向成像方法，特别是一种基于包络校正的方位ncs成像方法、系统、介质及设备。

背景技术：

在高分辨大斜视sar(syntheticapertureradar，合成孔径雷达)中，方位聚焦深度有限，表现为偏离方位场景中心的目标距离弯曲不能够完全校直，最后的图像散焦。一种有效的解决方法是采用方位ncs(nonlinearchirpscaling，非线性调频变标)处理，即通过方位相位的变标，增大方位聚焦深度，改善成像质量。然而，方位ncs处理也存在一定的局限，即仅仅对相位进行变标处理，对包络没有处理，尤其在高分辨(大)斜视下距离弯曲仍然不能够完全校直。

技术实现要素：

针对上述技术问题，本发明提供一种基于包络校正的方位ncs成像方法、系统、介质及设备。

本发明解决上述技术问题的技术方案如下：一种基于包络校正的方位ncs成像方法，包括：

步骤1、将基频回波数据进行距离fft变换，使数据变换到距离频域-方位时域后，进行距离脉压及走动校正；

步骤2、将经过距离脉压及走动校正的数据进行方位fft变换，使数据变换到二维频域后，依次进行弯曲校正和二维ifft变换，使数据变换到二维时域，得到第一sar图像；

步骤3、将所述第一sar图像进行二维fft变换，使数据变换到二维频域后，依次进行脉压和二维ifft变换，使数据变换到二维时域，得到第二sar图像；

步骤4、将所述第二sar图像沿方位维划分小块，并对各小块数据进行二维fft变换，使数据变换到二维频域后，依次进行包络校正和二维ifft变换，使数据变换到二维时域，再将所述各小块数据沿方位维在时域进行拼接，得到第三sar图像；

步骤5、将所述第三sar图像进行二维fft变换，使数据变换到二维频域后，进行方位散焦恢复；

步骤6、将经过方位散焦恢复的数据进行距离ifft变换，使数据变换到距离时域-方位频域后，依次进行方位高次项补偿和方位ncs变标处理，得到第四sar图像。

为实现上述发明目的，本发明还提供一种基于包络校正的方位ncs成像系统，包括：

第一变换模块，用于将基频回波数据进行距离fft变换，使数据变换到距离频域-方位时域后，进行距离脉压及走动校正；

第二变换模块，用于将经过距离脉压及走动校正的数据进行方位fft变换，使数据变换到二维频域后，依次进行弯曲校正和二维ifft变换，使数据变换到二维时域，得到第一sar图像；

第三变换模块，用于将所述第一sar图像进行二维fft变换，使数据变换到二维频域后，依次进行脉压和二维ifft变换，使数据变换到二维时域，得到第二sar图像；

第四变换模块，用于将所述第二sar图像沿方位维划分小块，并对各小块数据进行二维fft变换，使数据变换到二维频域后，依次进行包络校正和二维ifft变换，使数据变换到二维时域，再将所述各小块数据沿方位维在时域进行拼接，得到第三sar图像；

第五变换模块，用于将所述第三sar图像进行二维fft变换，使数据变换到二维频域后，进行方位散焦恢复；

第六变换模块，用于将经过方位散焦恢复的数据进行距离ifft变换，使数据变换到距离时域-方位频域后，依次进行方位高次项补偿和方位ncs变标处理，得到第四sar图像。

本发明还提供一种计算机可读存储介质，包括指令，其当所述指令在计算机上运行时，使所述计算机执行上述方法。

本发明还提供一种计算机设备，包括存储器、处理器及存储在所述存储器上的并可在所述处理器上运行的计算机程序，所述处理器执行所述程序时实现上述方法。

本发明的有益效果是：首先建立距离脉压及走动校正后二维频域信号模型，然后进行弯曲校正，接着进行包络校正，最后对方位频率高次项进行补偿，并进行ncs变标处理，得到聚焦良好的sar图像。本发明在高分辨(大)斜视应用下，能够显著增加方位聚焦深度，改善图像质量。

附图说明

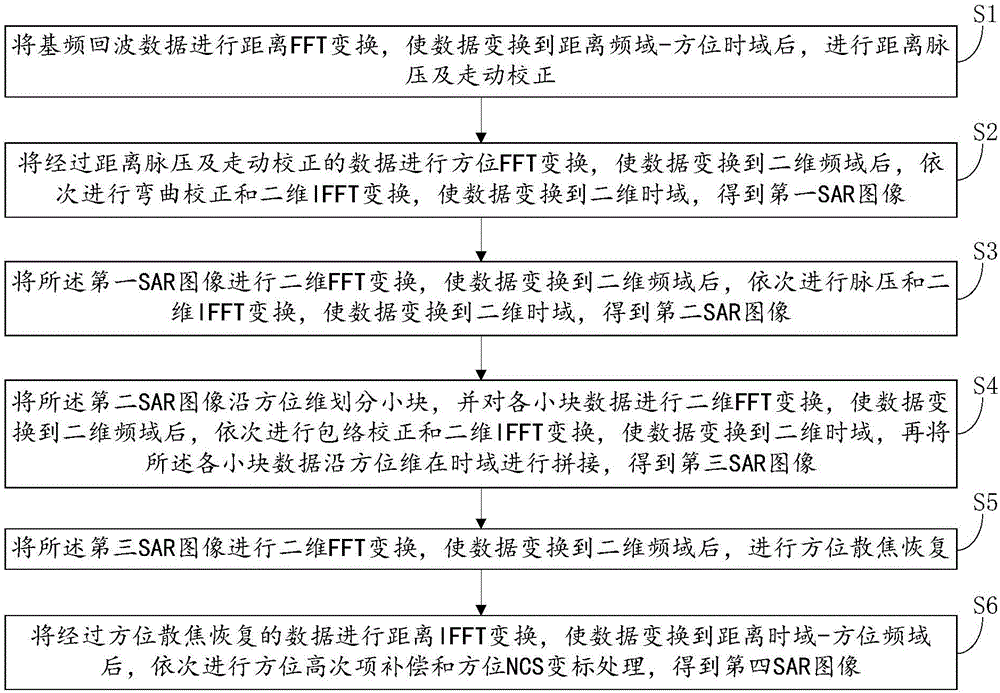
图1为本发明实施例提供的一种基于包络校正的方位ncs成像方法的流程图；

图2为斜视成像几何关系图；

图3为弯曲校正后图像(未包络校正)；

图4为弯曲校正后图像(包络校正后)；

图5为sar点阵目标；

图6为场景中心目标图像；

图7为场景边缘目标图像。

具体实施方式

以下结合附图对本发明的原理和特征进行描述，所举实例只用于解释本发明，并非用于限定本发明的范围。

图1为本发明实施例提供的一种基于包络校正的方位ncs成像方法的流程图，如图1所示，该方法包括：

s1、将基频回波数据进行距离fft变换，使数据变换到距离频域-方位时域后，进行距离脉压及走动校正；

具体的，基频回波数据为：

其中，为距离时间，tm为方位时间，γ为调频率，c为光速，fc为载波频率；

斜视成像几何关系如图2所示，along-track为沿航向(飞行)方向，载机以速度v作匀速直线飞行，在tm＝0时刻，载机位于o1点，点目标位于p点，过o1垂直于飞行方向的直线o1o2与过p点平行于飞行方向的直线po2交于o2点，波束指向为o1o4，斜视角为θ0，经过tm时间，载机运动到o3点，波束在地面投影为o5点。设o1o4＝rn，po4＝xn，po3＝r(tm)，则r(tm)的表达式为：

令fr为距离频率，将式(1)进行距离fft，使数据变换到距离频域-方位时域，得：

定义距离脉压及走动校正函数为：

式(3)乘以式(4)，得：

该步骤中，对数据进行距离脉压后，使目标能量在距离维得到集中，走动校正后，方位频谱中心移动到零频。

s2、将经过距离脉压及走动校正的数据进行方位fft变换，使数据变换到二维频域后，依次进行弯曲校正和二维ifft变换，使数据变换到二维时域，得到第一sar图像；

令fa为方位频率，式(5)进行方位fft，得：

对式(6)进行级数展开，如下所示。

式(7)中，为与fr和fa无关的系数。

距离脉压和走动校正后，目标图像呈现为对称的曲线，通过弯曲校正把曲线校正成直线，然后才能沿方位维进行脉冲压缩得到方位维也能量集中的目标图像。定义一个新的斜距变量rr，令rr＝rn+xnsinθ0，代入式(7)，得：

令rs表示场景中心斜距，弯曲校正函数为：

忽略式(8)中等号右边第三行rr与rs的差别，即忽略弯曲校正的误差，这可以通过距离维分块弯曲校正实现，如果距离分块，那么rs对应每个距离小块中心对应的斜距。式(8)乘以式(9)，得：

式(10)为弯曲校正后的二维频谱。对式(10)进行二维ifft操作，变换到二维时域，得：

式(11)为弯曲校正后的图像。

s3、将所述第一sar图像进行二维fft变换，使数据变换到二维频域后，依次进行脉压和二维ifft变换，使数据变换到二维时域，得到第二sar图像；

具体的，到当前为止，仅进行了距离脉压、走动校正、弯曲校正操作，方位维还没有进行脉压，因此信号能量在方位维是散布开的，图像在方位呈现一条线，而非一个凝聚的点。高分辨(大)斜视时，目标的能量线在弯曲校正后方位两端仍然呈现弯曲状，包络不直。包络没有完全校正影响方位聚焦的效果，因此，需要在方位脉压前把图像包络校直，即进行“包络校正”处理。

式(10)中，等号右边第四行为残留的弯曲校正误差，该项导致弯曲校正后包络仍然不直。重写如下：

式(12)中，fr为距离频率，故该项能够导致图像在距离维弯曲“校不直”。xn为点目标的方位位置坐标，显然，xn越大，式(12)相位越大，弯曲校正残留项sres(fr,fa)对包络的影响越大。如果不进行包络校正，要想成像效果好，则需要xn小到使sres(fr,fa)的影响可以忽略，而对xn的要求限制了方位能成像的范围，即方位聚焦深度。因而说，进行包络校正能够增大方位聚焦深度。

要校正式(12)对应的sres(fr,fa)，需要相对较准确地知道xn，然而无论是式(10)还是式(11)，信号能量在方位维都是散布开的，目标在方位没有聚焦，因而xn也无从说起。为了得到xn，可先对图像进行方位粗聚焦，把式(11)变换到二维频域，得：

在公式形式上，式(13)与式(10)完全一样，但式(13)是通过对方位完整孔径数据进行二维傅里叶变换得到的，而式(10)可能只是沿方位维所分的某一个小块数据，因为走动校正后方位维可以分块弯曲校正。设距离维场景中心距离(或距离小块的中心距离)为rs，调频斜率为：

方位粗聚焦对应的脉压函数为：

式(13)乘以式(15)，再二维ifft，得到粗聚焦完的sar图像，如下所示：

式(16)中，形式如式(11)所示，为方位未聚焦的sar图像，且存在包络弯曲。为方位粗聚焦的sar图像，虽然包络弯曲依然存在会导致聚焦效果不好，但却能够对目标进行方位定位，即xn可知。

s4、将所述第二sar图像沿方位维划分小块，并对各小块数据进行二维fft变换，使数据变换到二维频域后，依次进行包络校正和二维ifft变换，使数据变换到二维时域，再将所述各小块数据沿方位维在时域进行拼接，得到第三sar图像；

具体的，对式(16)数据沿方位维分小块处理，每个小块中目标的方位位置均近似为该块中心对应的方位坐标，对小块数据进行二维fft，得到：

定义包络校正函数为：

式(18)乘以式(17)，在二维ifft，得：

式(19)对应的小块已经完成包络校正，把所有小块沿方位维在时域拼接起来，得到粗聚焦的sar图像，但包络校正却已经完成。

s5、将所述第三sar图像进行二维fft变换，使数据变换到二维频域后，进行方位散焦恢复；

具体的，式(19)变换到二维频域，得：

式(20)除以式(15)的共轭进行方位散焦恢复，得：

式(21)中，scroase_recover(fr,fa)的包络完全校直了，并且恢复到方位维没有聚焦状态。

s6、将经过方位散焦恢复的数据进行距离ifft变换，使数据变换到距离时域-方位频域后，依次进行方位高次项补偿和方位ncs变标处理，得到第四sar图像。

上面详细给出了方位粗聚焦、分块包络校正、块拼接、方位散焦恢复的过程，从公式推导的等效上来说，式(21)如下所示：

式(22)为包络校正后的二维频谱，能够有效地把距离弯曲全部校直。式(22)进行距离ifft，得到距离时域、方位频域数据，如下所示：

方位高次项补偿函数为：

式(23)乘以式(24)，得：

令xn＝vt0，t0为以时间形式表示的目标方位位置。把xn＝vt0代入式(25)，得：

根据式(26)对t0进行方位ncs变标处理，即可得到聚焦的sar图像，如下所示：

式(27)中，为距离维时间，tm为方位维时间，p为ncs变标系数。

本发明还提供一种基于包络校正的方位ncs成像系统，包括：

第一变换模块，用于将基频回波数据进行距离fft变换，使数据变换到距离频域-方位时域后，进行距离脉压及走动校正；

第二变换模块，用于将经过距离脉压及走动校正的数据进行方位fft变换，使数据变换到二维频域后，依次进行弯曲校正和二维ifft变换，使数据变换到二维时域，得到第一sar图像；

第三变换模块，用于将所述第一sar图像进行二维fft变换，使数据变换到二维频域后，依次进行脉压和二维ifft变换，使数据变换到二维时域，得到第二sar图像；

第四变换模块，用于将所述第二sar图像沿方位维划分小块，并对各小块数据进行二维fft变换，使数据变换到二维频域后，依次进行包络校正和二维ifft变换，使数据变换到二维时域，再将所述各小块数据沿方位维在时域进行拼接，得到第三sar图像；

第五变换模块，用于将所述第三sar图像进行二维fft变换，使数据变换到二维频域后，进行方位散焦恢复；

第六变换模块，用于将经过方位散焦恢复的数据进行距离ifft变换，使数据变换到距离时域-方位频域后，依次进行方位高次项补偿和方位ncs变标处理，得到第四sar图像。

本发明还提供一种计算机可读存储介质，包括指令，其当所述指令在计算机上运行时，使所述计算机执行上述方法。

本发明还提供一种计算机设备，包括存储器、处理器及存储在所述存储器上的并可在所述处理器上运行的计算机程序，所述处理器执行所述程序时实现上述方法。

雷达参数如表1所示。

表1雷达参数

按照图2、表1参数进行点目标仿真，进行如下成像处理：

步骤一：距离脉压及走动校正

数据进行距离fft，变到距离频域，进行距离脉压及走动校正处理，得到式(5)，然后距离ifft，变换到距离时域。

步骤二：弯曲校正

把步骤一处理完的数据进行二维fft，变换二维频域，进行弯曲校正，得到式(10)；再二维ifft，变换到二维时域，得到式(11)，从而得到弯曲校正后的完整大图(式(11))。在高分辨(大)斜视应用下，弯曲校正后曲线两端仍存在一定的弯曲，如图3所示。

步骤三：包络校正

把弯曲校正后的数据(式(11))变换到二维频域，得到式(13)，乘以粗聚焦脉压函数式(15)，再二维ifft，得到粗聚焦的sar图像(式(16))。

把粗聚焦图像沿方位划分小块，各小块进行二维fft，得到二维频域信号(式(17))，式(17)乘以包络校正函数式(18)，然后二维ifft，变换二维时域，得到式(19)，把时域小块数据沿方位维拼接，得到包络校正完毕并且粗聚焦的sar图像。

接下来进行散焦恢复。把sar图像变换到二维频域(如式(20))，再除以粗聚焦脉压函数式(15)，得到式(21)，式(21)的显式表达式如式(22)所示。把式(22)二维ifft变换到二维时域，得到包络校正完毕的sar图像。此时，弯曲曲线两端也都被校直了，如图4所示。

步骤四：方位ncs处理

把步骤三处理结果进行方位fft，得到距离时域、方位频域数据，如式(23)所示，乘以方位高次项补偿函数式(24)，得到式(25)，再进行的变量替换，并方位ncs变标处理，得到聚焦良好的sar图像(式(27))。

完整场景点阵图像如图5所示，场景中心目标如图6所示，场景边缘点目标如图7所示。

以上所述仅为本发明的较佳实施例，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。