一种卫星精密定轨方法及装置与流程
本发明涉及卫星导航技术,尤其涉及一种卫星精密定轨方法及装置。
背景技术:
卫星导航定位系统(gnss)能够提供全球范围内实时的定位服务,并在世界各国的许多行业中得到了广泛的应用。目前标准的gnss定位技术精度大约为5-10米。对于精度要求更高的应用,通常需要使用精密定位的方法。用户通过接收导航卫星发送的导航信号,并以导航卫星作为动态己知点,利用伪距等观测信息实时地测定运动载体的在航位置和速度,进而完成导航。
实时获取精确的卫星轨道,是实现精密卫星导航定位的关键技术。目前,为提高导航精度,卫星导航系统还可以包括卫星导航增强系统主要分为星基增强系统(sbas)和地基增强系统(gbas)两大类。星基增强系统如美国的广域增强系统(waas)、俄罗斯的差分校正和监测系统(sdcm)等,地基增强系统如美国的局域增强系统(laas)等。使用增强系统之后,卫星静态定位精度可以达到厘米级,动态精度可以达到米级(车道级)。
目前,卫星轨道的确定方法主要包括3种:地面监测站定轨、星上自主定轨和事后精密定轨。目前,gnss系统,包括gps,glonass,bds等都使用少数的地面跟踪站实现轨道全弧段观测,然后计算和预报卫星轨道,上注到导航卫星。
地基增强通过提供差分修正信号,可达到提高卫星导航精度的目的;优化后的定位精度可以从毫米级至亚米级不等。基于连续运行的永久参考站,解算出的修正数包括区域信号(类似cors信号)和广域差分信号(类似sbas),播发方式包括移动网络/uhf电台/同步卫星等。基于地基增强系统播发非差综合改正信息的方式改正流动站处相应误差,从而达到模糊度参数与位置参数的快速分离,可在几个历元内固定模糊度参数,实现实时的差分定位,如rtk等,具有高精度、高实时性等优势,目前地基增强系统中的精密定位的方法有差分定位方法和精密单点定位方法。其中,差分定位方法包括局域差分方法和广域差分方法。广域差分方法和精密单点定位都需要通过地面监测网的数据计算出各自精密的信号偏差,精密轨道等,然后在用户端使用这些精密轨道和钟差精细改正来提高定位精度。局域差分方法主要是将参考站的观测数据和坐标直接播放给用户,在用户端通过观测值差分的方式消除各自误差的影响,实现高精度相对定位。但是,广域差分方法缺乏精密电离层模型支持,需要20-30分钟收敛才能获得厘米级的定位结果;局域差分方法中,需要用户接收机与参考站之间的距离在一定范围内,对地基监测网络布站密度要求较高。
sbas(satellite-basedaugmentationsystem)星基增强系统,通过地球静止轨道(geo)卫星搭载卫星导航增强信号转发器,可以向用户播发星历误差、卫星钟差、电离层延迟等多种修正信息,实现对于原有卫星导航系统定位精度的改进,从而成为各航天大国竞相发展的手段。
星上自主定轨是依靠星上的gnss接收机或惯性测量单元进行轨道确定,其中,基于gnss观测值的星上自主定轨方法能提供实时自主连续的卫星轨道,但是,由于受gnss导航卫星广播星历的轨道误差和钟差的影响,基于gnss观测值的星上自主定轨通常只能获得数米量级的定轨精度。为获得高精度的定轨,星基增强卫星主要分布在geo轨道,分为面向民航等用户的广域差分完好性增强与面向测绘等高精度用户的广域精密定位增强,具备广域覆盖的特点,但是目前的广域精密定位技术收敛时间长,难以形成面实时性要求较高的pnt应用,需要解决其收敛时间较慢的问题。
技术实现要素:
本发明实施例提供一种卫星精密定轨方法及装置,用于有效提高精密定轨的收敛时间。
本发明实施例提供一种卫星精密定轨方法,该方法包括:
获取地面接收机确定的导航卫星的第一观测数据和低轨卫星接收机确定的所述导航卫星的第二观测数据;
确定所述地面接收机的第一观测方程和所述低轨卫星接收机的第二观测方程;
根据所述第一观测数据和所述第二观测数据,解算所述第一观测方程和所述第二观测方程,从而确定所述导航卫星的轨道位置。
一种可能的实现方式,所述第二观测数据包括载波相位观测数据;所述第二观测数据通过以下方式获得,包括:
低轨卫星接收机若确定所述低轨卫星接收机的载波跟踪环路的跟踪状态为锁定状态,则根据测量精度确定所述载波跟踪环路的滤波器组合;
将获得的导航卫星的信号输入至所述载波跟踪环路的滤波器组合,并将输出的载波相位数据作为所述第二观测数据中的载波相位观测数据。
一种可能的实现方式,所述第一观测方程为:
ygroundi=fgb(xbdi,xoi,ti)+ξbdi;
其中,ygroundi为在ti时刻的第一观测数据;fgb表示地面接收机在ti时刻的观测函数;xbdi为导航卫星的轨道位置;xoi表示第一观测方程中的观测模型的参数;ξgroundi为所述第一观测数据的观测误差;
所述第二观测方程为:
yleoi=flb(xbdi,xleoi,xoi,ti)+ξleoi;
其中,yleoi为在ti时刻的第二观测数据;flb为低轨卫星接收机在ti时刻的观测函数;xbdi为导航卫星的轨道位置;xleoi为低轨卫星的轨道位置;xoi为第二观测方程中的观测模型的参数;ξleoi为所述第二观测数据的观测误差。
一种可能的实现方式,所述第一观测数据和所述第二观测数据均为双频观测数据;
所述确定所述地面接收机的第一观测方程和所述低轨卫星接收机的第二观测方程,包括:
根据双频观测数据,消除所述第一观测方程和所述第二观测方程中的电离层延迟误差,得到消除后的第一观测方程和第二观测方程。
一种可能的实现方式,所述第一观测方程中的观测函数包括伪距观测函数和载波相位观测函数;所述第二观测方程中的观测函数包括伪距观测函数和载波相位观测函数;
所述第一观测方程的伪距观测函数为:
所述第二观测方程的伪距观测函数为:
所述第一观测方程的载波相位观测函数为:
所述第二观测方程的载波相位观测函数为:
其中:λlc为无电离层组合相位波长,p表示导航卫星;
本发明实施例提供一种卫星精密定轨装置,该方法包括:
收发单元,用于获取地面接收机确定的导航卫星的第一观测数据和低轨卫星接收机确定的所述导航卫星的第二观测数据;
处理单元,用于确定所述地面接收机的第一观测方程和所述低轨卫星接收机的第二观测方程;根据所述第一观测数据和所述第二观测数据,解算所述第一观测方程和所述第二观测方程,从而确定所述导航卫星的轨道位置。
一种可能的实现方式,所述处理单元,用于若确定所述低轨卫星接收机的载波跟踪环路的跟踪状态为锁定状态,则根据测量精度确定所述载波跟踪环路的滤波器组合;将获得的导航卫星的信号输入至所述载波跟踪环路的滤波器组合,并将输出的载波相位数据作为所述第二观测数据中的载波相位观测数据。
一种可能的实现方式,所述第一观测方程为:
ygroundi=fgb(xbdi,xoi,ti)+ξbdi;
其中,ygroundi为在ti时刻的第一观测数据;fgb表示地面接收机在ti时刻的观测函数;xbdi为导航卫星的轨道位置;xoi表示第一观测方程中的观测模型的参数;ξgroundi为所述第一观测数据的观测误差;
所述第二观测方程为:
yleoi=flb(xbdi,xleoi,xoi,ti)+ξleoi;
其中,yleoi为在ti时刻的第二观测数据;flb为低轨卫星接收机在ti时刻的观测函数;xbdi为导航卫星的轨道位置;xleoi为低轨卫星的轨道位置;xoi为第二观测方程中的观测模型的参数;ξleoi为所述第二观测数据的观测误差。
一种可能的实现方式,所述第一观测数据和所述第二观测数据均为双频观测数据;
所述处理单元,具体用于根据双频观测数据,消除所述第一观测方程和所述第二观测方程中的电离层延迟误差,得到消除后的第一观测方程和第二观测方程。
一种可能的实现方式,所述第一观测方程中的观测函数包括伪距观测函数和载波相位观测函数;所述第二观测方程中的观测函数包括伪距观测函数和载波相位观测函数;
所述第一观测方程的伪距观测函数为:
所述第二观测方程的伪距观测函数为:
所述第一观测方程的载波相位观测函数为:
所述第二观测方程的载波相位观测函数为:
其中:λlc为无电离层组合相位波长,p表示导航卫星;
本发明实施例提供一种计算机存储介质,存储有计算机可执行指令,所述计算机可执行指令用于执行如本发明实施例提供任一项的方法。
本发明实施例提供一种电子设备,包括:
至少一个处理器;
以及与所述至少一个处理器通信连接的存储器;
其中,所述存储器存储有可被所述至少一个处理器执行的指令,所述指令被所述至少一个处理器执行,以使所述至少一个处理器能够执行如本发明实施例提供的任一项的方法。
本发明实施例中,地面接收机和低轨卫星的接收机在当前定位时刻确定对导航卫星的第一观测值和第二观测值,分别对导航卫星的精密轨道和低轨卫星的精密轨道进行解算,由于低轨卫星相对地面运动速度较快(角速度大),观测数据几何变化快,可加快载波相位整周模糊度估计收敛速度,大幅提高定位精度并缩短高精度定位收敛时间。因此,通过结合地面的观测数据和低轨卫星的观测数据,实现了对导航卫星的精密定轨的同时,减少了收敛时间。
附图说明
为了更清楚地说明本发明实施例的技术方案,下面将对本发明实施例中所需要使用的附图作简单地介绍,显而易见地,下面所介绍的附图仅仅是本发明的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动的前提下,还可以根据这些附图获得其他的附图。
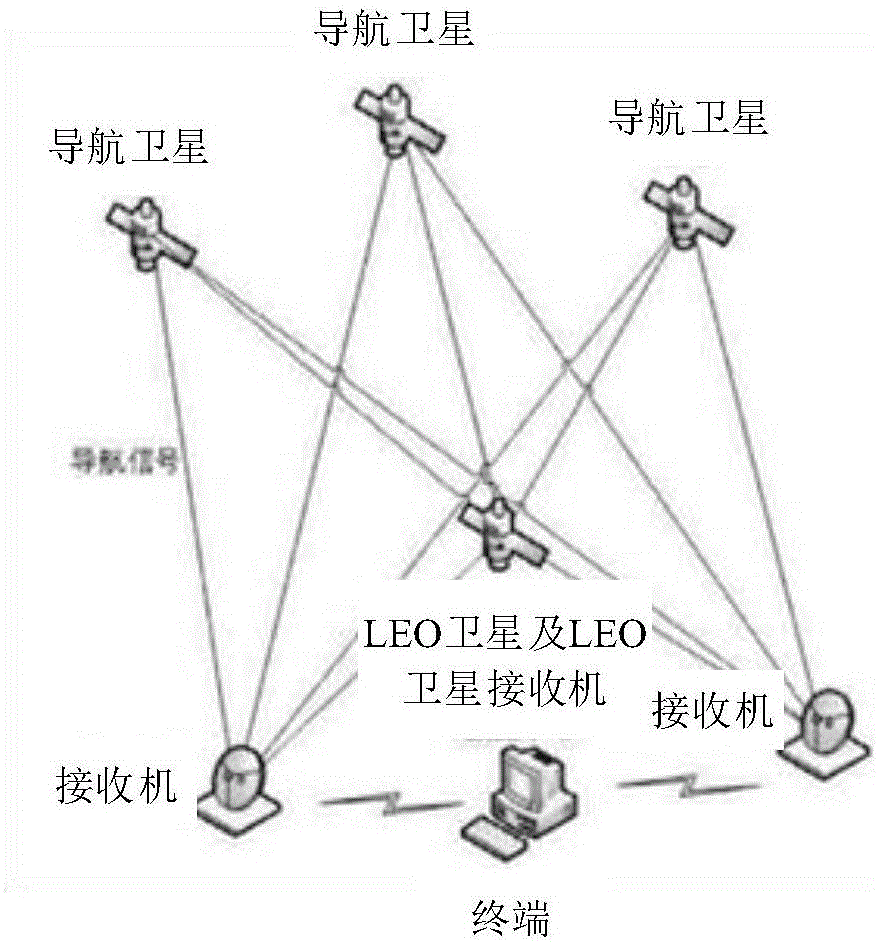
图1示出了本发明实施例提供的一种卫星定位方法的系统架构示意图;
图2示出了本发明实施例提供的一种卫星定位方法的流程示意图;
图3示出了本发明实施例提供的一种卫星定位方法的流程示意图;
图4示出了本发明实施例提供的一种卫星定位方法的流程示意图;
图5示出了本发明实施例提供的一种卫星定位方法的流程示意图;
图6示出了本发明实施例提供的一种卫星定位装置的结构示意图。
具体实施方式
为使本发明实施例的目的、技术方案和优点更加清楚,下面将结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚、完整地描述。
下面介绍本发明实施例的技术背景。
2015年,美国波音公司获得了美国军方约1.6亿美元合同,进一步开展基于铱星的gps导航增强技术研究和应用实验。为此组建了新的研究团队,主要参与者更变为satelles公司。新的低轨增强技术基于铱星系统新设置的gps导航增强专用stl(satellestimeandlocation)服务业务,在igps的基础上,进一步强化增强功能;国内低轨导航增强已经成为研究热点,多个星座计划或高校已经围绕低轨导航增强做了大量的体制论证工作,单高实时高精度服务尚处于空白;国外下一代铱星已经启动了低轨导航增强系统的建设,领先一步,有望实现低轨导航增强,并形成军民商应用;国内,低轨导航增强已经成为研究热点,多个星座计划或高校已经围绕低轨导航增强做了大量的体制论证工作,但都刚刚起步,高实时高精度服务尚处于空白。
如图1所示,低轨卫星相对地面运动速度较快,角速度大,观测数据几何变化快,可加快载波相位整周模糊度估计收敛速度,大幅提高定位精度并缩短高精度定位收敛时间,因此,相对传统的增强服务,由于leo卫星对地面运动较快,星座的几何构型变化较快,通过实施精密定轨后的leo卫星,向客户播发leo星座卫星导航和增强信号有利于载波相位模糊度参数的快速收敛和固定,为解决精密单点定位ppp技术收敛时间过长的问题提供契机。本发明实施例采用leo卫星上的星载接收机获取导航卫星的观测数据,以减少导航卫星定轨所需的收敛时间。
相对于传统的卫星导航设备,本发明实施例中的接收机由于安装在低轨卫星上,速度和动态都远大于车载、机载卫星导航设备,需要在卫星信号的捕获与跟踪算法上作相应的调整保证捕获灵敏度以及载波跟踪环的跟踪精度。
为了实现高实时高精度服务,作为核心载荷的多频星载接收机的硬件主要瓶颈在于制造卫星载荷复杂度高,软件算法则需要验证高精度轨道钟差改正数解算、卫星相位延迟解算、区域高精度电离层建模、区域观测数据与leo观测数据联合定轨、实时区域站观测数据实时精密钟差解算模型、leo精密钟差确定等关键技术。
下面结合附图介绍本发明实施例提供的技术方案。
如图2所示,本发明实施例提供一种卫星精密定轨方法,该方法包括:
步骤201:获取地面接收机确定的导航卫星的第一观测数据和低轨卫星接收机确定的所述导航卫星的第二观测数据;
步骤202:确定所述地面接收机的第一观测方程和所述低轨卫星接收机的第二观测方程;
步骤203:根据所述第一观测数据和所述第二观测数据,解算所述第一观测方程和所述第二观测方程,从而确定所述导航卫星的轨道位置。
需要说明的是,根据不同应用场合,星载接收机的功能不同,一般来说多数星载接收机用于卫星定轨、授时和定姿等。定轨精度一般在1-2米,根据频点和星座规划不同,一般分单星座单频,多星座多频接收机,本发明实施例中,为了实现模糊度搜索效率提高,可以更快获取模糊度整数解,可以采用双星座双频星载接收机。具体的,该接收机可以同时接收gps的l1、l2和/或北斗卫星b1、b2频点的信号,以提供双频的高精度观测数据。
本发明实施例中,地面接收机和低轨卫星的接收机在当前定位时刻确定对导航卫星的第一观测值和第二观测值,分别对导航卫星的精密轨道和低轨卫星的精密轨道进行解算,由于低轨卫星相对地面运动速度较快(角速度大),观测数据几何变化快,可加快载波相位整周模糊度估计收敛速度,大幅提高定位精度并缩短高精度定位收敛时间。因此,通过结合地面的观测数据和低轨卫星的观测数据,实现了对导航卫星的精密定轨的同时,减少了收敛时间。
本发明的技术解决问题首先是观测数据生成问题是leo卫星观测弧段短、运行速度快、大气阻力影响大,导致地面站所接收到的leo卫星观测数据中周跳较多、粗差大;本发明实施例中的星载接收机环路使用考虑到角速度比较大,速度很快,载波环路机制需要保证跟踪的准确性,常见的接收机的载波相位观测数据一般只用来平滑伪距和多普勒的计算,计算时只需要载波相位前后时刻的增量数据减去中频累加部分。
而如果用于非差的ppp精密定位,则需要连续的载波相位累加值输出,需要考虑到钟差调整带来的影响。
一种可能的实现方式,所述第二观测数据包括载波相位观测数据;所述第二观测数据通过以下方式获得,包括:
低轨卫星接收机若确定所述低轨卫星接收机的载波跟踪环路的跟踪状态为锁定状态,则根据测量精度确定所述载波跟踪环路的滤波器组合;
将获得的导航卫星的信号输入至所述载波跟踪环路的滤波器组合,并将输出的载波相位数据作为所述第二观测数据中的载波相位观测数据。
本发明实施例中,载波环路控制主要包括锁频环fll、二阶锁相环pll2以及2阶锁频辅助3阶锁相环的机制下切换。
扩频信号的捕获方法主要有串行捕获、并行捕获和基于fft的快速捕获。串行捕获方法是一个频域和时域的顺序二维搜索过程,其捕获时间较长;并行捕获方法采用多个捕获通道,各个通道分别并行完成接收信号与不同码相位和不同多普勒频率的本地再生信号的相关计算,相对于串行捕获,捕获速度大。
直扩信号的捕获过程就是通过在时间域和频域进行二维搜索来检测y的模平方是否超过由噪声统计决定的门限值,基于fft的快速捕获方法可以在给定ω下,在同一时间段内搜索伪码所有相位,因此捕获速度很高。
在高动态环境下,由于多普勒频移的不确定性,直接捕获载波相位有较大的难度;另外,为了提高动态跟踪能力,势必增加环路带宽,而增加环路带宽就会引入较大的跟踪误差。在初始捕获时,采用fft可以对信号进行快速捕获,为了解决高动态捕获能力和提高跟踪精度的矛盾,在需要提高精度时,载波环还可以采用fll+pll混合载波跟踪算法。fll环直接跟踪载波频率,通过载波鉴频器输出多普勒频率估计误差,具有较好的动态性能,但跟踪精度比pll环的低。
简单的pll由频率基准、相位检波器、电荷泵、环路滤波器和压控振荡器(vco)组成。基于pll技术的频率合成器将增加两个分频器:一个用于降低基准频率,另一个则用于对vco进行分频。pll是作为闭环控制系统工作,用于比较基准信号与vco的相位。增设基准和反馈分频器的频率合成器负责比较两个由分频器的设定值调节相位。该相位比较在相位检波器中完成,该相位-频率检波器生成一个误差电压,此误差电压在±2π的相位误差范围内近似为线性,并在误差大于±2π的情况下保持恒定。相位-频率比较器所采用的这种双模式操作可生成针对大频率误差(比如,当pll在上电期间起动时)的较快的pll锁定时间,并避免被锁定于谐波之上。
鉴相器有两个输入,分别是输入信号和压控振荡器的输出信号,在二者相位差和频率差不是很大的情况下,鉴相器的输出与两输入信号之差成正比,鉴相器的输出为模拟信号,其通过低通滤波器虑除高频杂波,后进入压控振荡器,压控振荡器的输出频率随其输入电压的改变而改变。从原理图上看,pll实际上是一负反馈系统,只要输入信号在正常范围内,输出信号在“一定时间内”都能跟上。输入信号发生变化后,输出信号跟踪输入信号的过程称之为捕获;输出信号跟踪完毕时称之为锁定;输入信号变化过快导致输出信号无法跟踪时称为失锁。通过pll可以方便实现n倍频。
为进一步提高精度,可以采用二阶锁相环pll2以及2阶锁频辅助3阶锁相环等方式。
具体的,pll2和fll2+pll3中的时域和频域的公式如下:
2阶pll环路滤波器时域核心公式如下:
其中xn表示输入信号,yn表示输出信号,un表示频域的信号,t表示时间,ω0表示初始角速度;
变换到z域可以得到:
则有:
利用z变换变换到时域,可以得到输出信号:
2阶锁频环辅助3阶锁相环环路滤波器核心公式如下:
转换到z域可以得到:
本发明实施例中,载波环路的调整和载波相位观测数据的生成机制和普通接收机不同;在获取载波相位观测数据时,根据失锁捕获以及跟踪精度,确定跟踪环路,以提高载波相位数据的精度。
在具体实施过程中,观测数据的质量和环路状态、环路精度评估机制和bit反转与否都相关,因此,在输出载波相位观测数据之前,还可以包括环路状态、环路精度评估和bit反转等参数的判断,以提高观测数据精度。
如图3所示,本发明实施例提供一种获取载波相位观测数据的方法,包括:
步骤301:接收导航卫星的直发信号,并将接收到的直发信号作为接收机中载波环路的输入信号;
步骤302:判断当前载波环路的锁定指示是否高于跟踪门限;若是,则执行复位,对所述直发信号重新跟踪;若否,则执行步骤303;
步骤303:根据当前环路滤波的需要,确定滤波器类型;若确定当前跟踪状态为初始状态或者当前跟踪精度较低,则执行步骤304;若确定当前跟踪状态为稳定跟踪或者当前跟踪精度较高,可以执行步骤305或步骤306,可以根据跟踪精度确定选择的环路;
步骤304:将输入信号依次输入至鉴频器,和fll环路滤波器,获得输出信号;
步骤305:将输入信号依次输入至鉴相器,和pll2环路滤波器,获得输出信号;
步骤306:将输入信号依次输入至鉴相器,和fll2+pll3环路滤波器,获得输出信号;
步骤307:将环路滤波器的输出信号输入至载波环路的数字控制振荡器nco,输出载波相位累加值;
步骤308:判断载波环路状态,若确定载波环路状态失锁,则执行步骤302;若确定载波环路状态为稳定跟踪,则执行步骤309;
步骤309:判断bt帧同步是否有效;若是,则执行步骤310;若否,则执行步骤313;
步骤310:判断环路跟踪精度是否满足要求;若是,则执行步骤311;若否,则执行步骤313;
步骤311:判断载波bit是否需要反转;若否,则执行步骤312;若是则执行步骤313;
步骤312:确定当前时刻的载波相位累加值,并将载波相位累加值作为输出的载波相位观测数据;
步骤313:确定载波相位观测数据无效。
通过上述方法,可以实现一个完整的环路控制和切换机制,以获得满足精度需要的载波相位观测数据。
为了实现非差的精密定位,本发明实施例中,由于卫星和接收机未校准的初始相位延迟,载波相位中所包含的模糊度信息要完成的保留下来,所以整数部分和小数部分的处理必须分开,以保留载波相位观测值任意一部分,提高定轨的精度。
如图4所示载波相位观测数据计算流程中所有的载波相位计算都是整数部分和小数部分分开,包括:
步骤401、将上一时刻的载波相位累加值、当前时刻的载波相位累加值、中频累加值和本地时钟调整量,输入至载波相位计算单元,确定出载波相位观测数据的整数部分和小数部分;
具体的,确定出载波相位观测数据的整数部分和小数部分为当前时刻载波相位累加值的整数部分和小数部分减去上一时刻的载波相位累加值整数部分和小数部分,再减去数字中频频率*测量时间间隔。
步骤402、对载波相位观测数据进行半周补偿,输出最终的载波相位观测数据。
需要说明的是,在载波相位观测数据计算流程中,同时需要把上一时刻载波相位观测值未调整部分减去,保证载波相位累加值的变化和伪距观测值保持一致。
本发明实施例提供的一种卫星精密定轨方法,具体处理过程可以包括:
步骤一、地面接收机和leo星载接收机接收导航卫星播发的导航直发信号,对直发信号进行捕获、跟踪;
步骤二、在每一历元,地面接收机对导航直发信号进行测量,产生伪距、载波相位的第一观测数据;leo星载接收机对导航直发信号进行测量,产生伪距、载波相位的第二观测数据;
步骤三、利用第一观测数据和第二观测数据建立第一观测方程和第二观测方程;
其中,地面接收机的第一观测方程和星载北斗接收机的第二观测方程可以分别表示:
ygroundi=fgb(xbdi,xoi,ti)+ξbdi
yleoi=flb(xbdi,xleoi,xoi,ti)+ξleoi
式中,ygroundi和yleoi分别表示地面和星载北斗接收机在ti时刻的观测值;fgb和flb分别表示地面和星载北斗接收机在ti时刻的观测函数;xoi和xoi分别表示除了xbdi和xleoi之外的其它待估参数,如钟差、模糊度、大气参数等;ξgroundi和ξleoi是相应观测值的观测误差。
其中,若确定存在多种卫星导航系统,则以一种卫星导航系统为基准,对其他卫星导航系统和低轨卫星观测数据进行归一化处理,得到统一时间基准观测方程;
步骤四、对第一观测数据和第二观测数据,进行周跳粗差的预处理。
步骤五、利用第一观测数据,第二观测数据,卫星精密钟差,以及精密轨道模型,进行观测方程的解算,得到导航卫星和leo卫星的精密定位和接收机钟差;
步骤六、通过通信链路接收地基监测网播发的非差综合改正信息,或者,leo卫星播发非差综合改正信息;
步骤七、根据接收非差综合改正信息计算用户概略位置相对每颗导航卫星和低轨卫星的误差改正参数;
步骤八、采用精密单点定位模式进行定位处理,授时和测速结果及载波相位模糊度参数等。
通过本申请提供的一种卫星精密定轨方法,可在全球获得近实时的精密定位、测速和授时结果。该星载接收机提供的双频观测数据结合gnss卫星精密轨道和钟差及硬件延迟建模信息以及地面站观测数据可实现快速实时的leo/gnss联合ppp定轨。
本发明的技术解决问题涉及到观测数据的处理问题,特别是关于双频载波相位处理的问题,关于ppp的研究主要基于双频观测数据,已经实现了静态mm-cm、动态cm-dm级的定位精度。
与单频精密单点定位不同的是,双频精密单点定位对双频伪距和相位观测值进行组合来消除电离层一阶项的影响。双频精密单点定位通常组成melbourne-wübbena和geometry-free组合,采用turbo-edit方法进行周跳探测。双频精密单点定位的观测模型及双频载波与伪距的无电离层组合观测方程为:下面通过一个具体实施例对本发明技术方案进行详细说明。
如图5所示,基于非差的ppp定轨的主要过程,可以包括:
步骤501、对第一观测数据和第二观测数据周跳粗差探测数据预处理。
步骤502、利用第一观测数据和第二观测数据建立第一观测方程和第二观测方程;
一种可能的实现方式,所述第一观测方程为:
ygroundi=fgb(xbdi,xoi,ti)+ξbdi;
其中,ygroundi为在ti时刻的第一观测数据;fgb表示地面接收机在ti时刻的观测函数;xbdi为导航卫星的轨道位置;xoi表示第一观测方程中的观测模型的参数;ξgroundi为所述第一观测数据的观测误差;
所述第二观测方程为:
yleoi=flb(xbdi,xleoi,xoi,ti)+ξleoi;
其中,yleoi为在ti时刻的第二观测数据;flb为低轨卫星接收机在ti时刻的观测函数;xbdi为导航卫星的轨道位置;xleoi为低轨卫星的轨道位置;xoi为第二观测方程中的观测模型的参数;ξleoi为所述第二观测数据的观测误差。
其中,地面接收机接收导航卫星的导航信号产生的第一观测数据包含多星座多频点伪距、载波相位和多普勒观测数据;leo星载接收机接收导航卫星的导航信号产生的第二观测数据。
第一观测方程可以包括载波相位观测方程和伪距方程;第二观测方程也可以包括载波相位观测方程和伪距方程。
一种可能的实现方式,所述第一观测数据和所述第二观测数据均为双频观测数据;所述确定所述地面接收机的第一观测方程和所述低轨卫星接收机的第二观测方程,包括:
根据双频观测数据,消除所述第一观测方程和所述第二观测方程中的电离层延迟误差,得到消除后的第一观测方程和第二观测方程。
在具体实施过程中,可以根据双频的第一观测数据和第二观测数据,构造无电离层组合的第一观测数据和无电离层组合的第二观测数据,消除一阶电离层延迟影响,减少未知参数,具体的,载波相位观测方程和伪距方程的模型为:
其中:λlc为无电离层组合相位波长,
在具体实施过程中,第一观测方程中的观测函数包括伪距观测函数和载波相位观测函数;第二观测方程中的观测函数包括伪距观测函数和载波相位观测函数;
所述第一观测方程的伪距观测函数为:
所述第二观测方程的伪距观测函数为:
所述第一观测方程的载波相位观测函数为:
所述第二观测方程的载波相位观测函数为:
其中:λlc为无电离层组合相位波长,p表示导航卫星;
其中,对流层延迟通常可以分为干分量和湿分量两部分。干分量可以通过模型进行改正,湿分量作为待估参数进行估计。为了减少待估参数的数量,可以使用映射函数将斜延迟投影到天顶方向,只估计一个天顶湿延迟。
利用相对论效应、地球自转、天线相位中心等模型对观测方程进行改正,消去部分参数,同时忽略残留的卫星轨道和钟差误差。
根据导航卫星和低轨卫星的运动方程和变分方程积分,就可以分别得到它们的初始参考轨道和状态转移矩阵;
根据卫星精密定轨问题的一般性描述可知,对导航卫星和低轨卫星的运动方程和变分方程积分,就可以分别得到它们的初始参考轨道和状态转移矩阵
式中,
根据初始参考轨道,对观测方程进行线性化。
具体的,在初始参考轨道的接收机近似位置进行泰勒展开,舍弃二阶项,得到:
其中,(x,y,z)为低轨卫星或导航卫星精密轨道坐标,(xr,0,yr,0,zr,0)为接收机近似位置。
于是观测方程可以简化写为:
v=aδx+l(23)
其中v为观测残差,a为系数矩阵,δx为包括接收机坐标改正、接收机钟差、对流层天顶湿延迟、载波相位模糊度在内的未知向量,l为计算向量。
步骤503、结合参数最优估计方法对线性化的观测方程进行解算,获得导航卫星和低轨卫星的精密定轨位置。
具体的,在进行参数估计和模糊度固定处理的具体实施过程中,可以采用最小二乘法或kalman滤波进行综合ppp处理。
星地联合定轨中存在观测数据量大、估计参数多的问题,所以在数据处理中需要使用实时预消除参数的方法消除法方程中失效的参数(包括历元参数、时段参数),使之有效地减小法方程的大小,加快法方程处理的时间。而且,如果在进行消参数的同时也把消除的参数与其它参数的联系方程保存起来,则可以在求解法方程后通过回代的方式恢复这些参数。
对于频繁的历元参数的消除,本项目将采取极为有效的索引策略来加快法方程的更新,极大地缩短了消参数的时间消耗;对于模糊度参数,本专利将定义好模糊度的有效时间段,在该模糊度参数刚消失时即将其从法方程中消去。从总体上优化软件的数据结构,减少函数间大型数组的传递和继承的时间,提高软件的运行效率。
下面将通过数学描述来说明参数预消除与恢复的基本流程。
设有误差方程:
将参数向量
现假设
对公式中的第二式两端同时乘以
再两式相加,得:
令
法方程的解为:
则可以恢复预消除参数向量
结合有:
由此可见,在消除参数向量
在kalman滤波中,需要提供合适的观测值随机模型以及状态向量动态模型。随机模型描述的是观测值的统计特性,通常用观测值的方差协方差阵表示。从观测方程可知,消电离层组合观测值是原始观测值的线性组合,假设不同频率上的观测值不相关,消电离层组合观测值的初始方差可以通过误差传播定律计算得到。具体的方差可以定义为初始方差和卫星高度角的函数。假设不同卫星、不同系统的观测值不相关,以及不同类型的观测值,即伪距和相位观测值不相关,就可以得到观测值的方差协方差阵。
针对状态向量的动态模型,静态接收机坐标可以表示为常数,动态接收机坐标和接收机钟差可以表示为随机游走或者一阶高斯马尔科夫过程,对流层天顶湿延迟可以表示为随机游走过程,载波相位模糊度参数可以表示为常数,于是得到状态方程。
xk=φ(tk,tk-1)xk-1+wk-1
式中,x为待估计的接收机坐标改正、接收机钟差等参数,φ为状态转移矩阵,wk-1为状态转移噪声。综合观测方程和状态方程,可应用标准kalman滤波过程进行参数估计。这里由于未进行卫星相位小数偏差改正,所以仅获得载波相位模糊度浮点解结果。若进一步利用低轨卫星增强信息中包含的卫星相位小数偏差改正进行观测方程改正,则可恢复模糊度的整数特性,实现模糊度固定,得到载波相位模糊度固定解结果,进一步缩短初始化时间,提高定位、测速和授时精度。
由于增加低轨卫星的观测数据,低轨卫星的快速移动特性极大提升了解算效率,从而使ppp收敛时间大幅降低。
步骤504、利用低轨卫星播发的导航卫星增强信息和模型进行误差改正。
如图6所示,本发明实施例提供一种卫星精密定轨装置,该方法包括:
收发单元601,用于获取地面接收机确定的导航卫星的第一观测数据和低轨卫星接收机确定的所述导航卫星的第二观测数据;
处理单元602,用于确定所述地面接收机的第一观测方程和所述低轨卫星接收机的第二观测方程;根据所述第一观测数据和所述第二观测数据,解算所述第一观测方程和所述第二观测方程,从而确定所述导航卫星的轨道位置。
一种可能的实现方式,所述处理单元602,用于若确定所述低轨卫星接收机的载波跟踪环路的跟踪状态为锁定状态,则根据测量精度确定所述载波跟踪环路的滤波器组合;将获得的导航卫星的信号输入至所述载波跟踪环路的滤波器组合,并将输出的载波相位数据作为所述第二观测数据中的载波相位观测数据。
一种可能的实现方式,所述第一观测方程为:
ygroundi=fgb(xbdi,xoi,ti)+ξbdi;
其中,ygroundi为在ti时刻的第一观测数据;fgb表示地面接收机在ti时刻的观测函数;xbdi为导航卫星的轨道位置;xoi表示第一观测方程中的观测模型的参数;ξgroundi为所述第一观测数据的观测误差;
所述第二观测方程为:
yleoi=flb(xbdi,xleoi,xoi,ti)+ξleoi;
其中,yleoi为在ti时刻的第二观测数据;flb为低轨卫星接收机在ti时刻的观测函数;xbdi为导航卫星的轨道位置;xleoi为低轨卫星的轨道位置;xoi为第二观测方程中的观测模型的参数;ξleoi为所述第二观测数据的观测误差。
一种可能的实现方式,所述第一观测数据和所述第二观测数据均为双频观测数据;
所述处理单元,具体用于根据双频观测数据,消除所述第一观测方程和所述第二观测方程中的电离层延迟误差,得到消除后的第一观测方程和第二观测方程。
一种可能的实现方式,所述第一观测方程中的观测函数包括伪距观测函数和载波相位观测函数;所述第二观测方程中的观测函数包括伪距观测函数和载波相位观测函数;
所述第一观测方程的伪距观测函数为:
所述第二观测方程的伪距观测函数为:
所述第一观测方程的载波相位观测函数为:
所述第二观测方程的载波相位观测函数为:
其中:λlc为无电离层组合相位波长,p表示导航卫星;
本发明实施例提供的实施、方法的电子设备,该电子设备包括:
一个或多个处理器以及存储器,以一个处理器为例。
执行数据同步方法的电子设备还可以包括:输入装置和输出装置。
处理器、存储器、输入装置和输出装置可以通过总线或者其他方式连接,以通过总线连接为例。
存储器作为一种非易失性计算机可读存储介质,可用于存储非易失性软件程序、非易失性计算机可执行程序以及模块,如本申请实施例中的数据库同步延迟的确定方法对应的程序指令/模块/单元。处理器通过运行存储在存储器中的非易失性软件程序、指令以及模块/单元,从而执行服务器或者智能终端的各种功能应用以及数据处理,即实现上述方法实施例数据库同步延迟的确定方法。
存储器可以包括存储程序区和存储数据区,其中,存储程序区可存储操作系统、至少一个功能所需要的应用程序;存储数据区可存储根据数据同步装置的使用所创建的数据等。此外,存储器可以包括高速随机存取存储器,还可以包括非易失性存储器,例如至少一个磁盘存储器件、闪存器件、或其他非易失性固态存储器件。在一些实施例中,存储器可选包括相对于处理器远程设置的存储器,这些远程存储器可以通过网络连接至数据库同步延迟的确定装置。上述网络的实例包括但不限于互联网、企业内部网、局域网、移动通信网及其组合。
输入装置可接收输入的数字或字符信息,以及产生与数据库同步延迟的确定装置的用户设置以及功能控制有关的键信号输入。输出装置可包括显示屏等显示设备。
所述一个或者多个模块存储在所述存储器中,当被所述一个或者多个处理器执行时,执行上述任意方法实施例中的数据库同步延迟的确定方法。
上述产品可执行本申请实施例所提供的方法,具备执行方法相应的功能模块和有益效果。未在本实施例中详尽描述的技术细节,可参见本申请实施例所提供的方法。
本申请实施例提供了一种计算机程序产品,其中,所述计算机程序产品包括存储在非暂态计算机可读存储介质上的计算机程序,所述计算机程序包括程序指令,其中,当所述程序指令被计算机执行时,使所述计算机执行本申请上述方法实施例中任一项数据库同步延迟的确定方法。
本领域内的技术人员应明白,本发明的实施例可提供为方法、系统、或计算机程序产品。因此,本发明可采用完全硬件实施例、完全软件实施例、或结合软件和硬件方面的实施例的形式。而且,本发明可采用在一个或多个其中包含有计算机可用程序代码的计算机可用存储介质(包括但不限于磁盘存储器、cd-rom、光学存储器等)上实施的计算机程序产品的形式。
本发明是参照根据本发明实施例的方法、设备(系统)、和计算机程序产品的流程图和/或方框图来描述的。应理解可由计算机程序指令实现流程图和/或方框图中的每一流程和/或方框、以及流程图和/或方框图中的流程和/或方框的结合。可提供这些计算机程序指令到通用计算机、专用计算机、嵌入式处理机或其他可编程数据处理设备的处理器以产生一个机器,使得通过计算机或其他可编程数据处理设备的处理器执行的指令产生用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的装置。
这些计算机程序指令也可存储在能引导计算机或其他可编程数据处理设备以特定方式工作的计算机可读存储器中,使得存储在该计算机可读存储器中的指令产生包括指令装置的制造品,该指令装置实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能。
这些计算机程序指令也可装载到计算机或其他可编程数据处理设备上,使得在计算机或其他可编程设备上执行一系列操作步骤以产生计算机实现的处理,从而在计算机或其他可编程设备上执行的指令提供用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的步骤。
尽管已描述了本发明的优选实施例,但本领域内的技术人员一旦得知了基本创造性概念,则可对这些实施例做出另外的变更和修改。所以,所附权利要求意欲解释为包括优选实施例以及落入本发明范围的所有变更和修改。
显然,本领域的技术人员可以对本发明进行各种改动和变型而不脱离本发明的精神和范围。这样,倘若本发明的这些修改和变型属于本发明权利要求及其等同技术的范围之内,则本发明也意图包含这些改动和变型在内。
- 还没有人留言评论。精彩留言会获得点赞!