一种采用异形蓝色噪声编码孔径的光谱成像方法与流程

本发明提供一种采用异形蓝噪声编码孔径的光谱成像方法，属于光电编码技术领域。

背景技术：

高光谱成像技术在紫外到近红外的光谱范围内，对目标物体在各个波段上进行成像，同时获得物体的空间信息和光谱信息，具有很高的空间分辨率和光谱分辨率。高光谱成像技术在空间遥感、军事侦察、农业和工业生产、生物医学等诸多领域均有重要应用，已被科技部纳入“地球观测与导航”重点专项之中。

随着光谱分辨率的提高，高光谱数据量迅速增长，这对高光谱图像采集、存储、传输和处理等提出了巨大挑战，制约了高光谱成像技术的发展。因此压缩高光谱成像(chsi)技术受到了国内外学者的广泛研究。2008年，wagadarikar等人将cs理论应用于光谱成像，首次提出了cassi技术，将高光谱图像的采样与压缩过程合二为一。

cassi技术采用编码孔径和色散元件，将原始的高光谱三维数据投影在ccd上，获得单次投影测量数据，然后通过cs重构算法由二维投影测量数据恢复出三维高光谱数据。但是单次投影会导致较多的光谱信息损失，不足以重构出高质量的高光谱数据。随后，davidkittle,henryarguello,y.wu等人对单次投影方法进行改进，提出了多次投影测量方法，提高了三维高光谱数据的重构质量。之后，研究人员又提出了彩色编码孔径方法(coloredcodedaperture,简称cca)，使高光谱数据可以在空间范围和光谱范围内同时被调制，提高了三维光谱数据的重构质量，但cca的制备成本较高。为了进一步改善高光谱图像的重建精度，研究人员又提出了多种编码孔径优化方法。这些方法根据cs理论的有限等距性质(restrictedisometryproperty，简称rip)对感知矩阵进行优化，尽量保证投影矩阵与稀疏基不相关。在光谱数据采集之前对编码孔径进行优化，提高了图像的重建质量。

但是，这些方法可能导致采样不均匀，这不足以捕获光谱图像的丰富结构信息。此外，优化过程通常是耗时的，并且将引入额外的计算复杂性。

ulichney在半色调领域提出了蓝噪声，蓝噪声是一种统计模型，描述了理想的非周期分布的点模式的空间和频谱特征。理想的蓝噪声半色调掩模版是由相同尺寸的随机抖动的点组成的图案，掩模版上的点尽可能均匀地分布，从而使采样均匀。correa等人根据cassi感知矩阵的rip性质设计了空间蓝噪声编码孔径。然而，correa提出的空间蓝噪声是基于正方形编码孔径的，不能提高编码孔径优化自由度。

综上所述，现有的设计cassi系统中编码孔径的方法有待进一步改善和提高。

技术实现要素：

有鉴于此，本发明的目的是提供一种采用异形蓝噪声编码孔径的光谱成像方法。

实现本发明的技术方案如下：

一种采用异形蓝噪声编码孔径的光谱成像方法，具体步骤为：

用光源照射待成像目标得到高光谱三维数据，高光谱三维数据经过透镜成像到六边形蓝噪声编码孔径上被编码孔径所调制，经过调制的高光谱三维数据经色散棱镜色散后通过透镜成像到ccd探测器上；

利用ccd探测器上探测的数据，恢复待成像目标的高光谱三维数据。

进一步地，本发明多次改变六边形蓝噪声编码孔径相对于探测器的平移量α，得到对应不同α的ccd探测器的探测数据。

进一步地，本发明根据如下欠定方程计算基ψ，根据所述ψ利用压缩感知重构算法恢复待成像目标的高光谱三维像，

y＝hψθ+ω

其中，θ表示稀疏系数，ω为ccd探测器多次测量的总噪声，y表示ccd探测器上得到的探测数据；

y＝[y¹,y²,...y^k]^t

h＝[h^1t,h^2t,...h^kt]^t

其中,k表示探测次数，t^k表示第k次探测蓝噪声六边形编码孔径所等效的矩形灰度编码孔径的透过率；diag(t^k)表示n²×n²的对角矩阵，t^k表示t^k的向量表示，0表示维度为n²×n²(l-1)的零矩阵，i表示n²×n²的单位矩阵，表示n²l×n²l的置换矩阵，其结构和下面的矩阵结构相似：

进一步地，本发明将六边形蓝噪声编码孔径所等效的灰度正方形编码孔径分成两类，

类型一，位于奇数列的编码孔径，与第(i，j)个孔径等价的灰度正方形编码孔径的透过率为：

类型二：位于偶数列的编码孔径，与第(i，j)个孔径等价的灰度正方形编码孔径的透过率为：

其中，α表示六边形编码孔径相对于探测器的平移量，tb表示六边形编码孔径的透过率，tg表示与六边形编码孔径等价的灰度正方形编码孔径的透过率。

有益效果

首先,本发明采用的编码孔径是以六边形像素代替正方形，形成蜂窝状阵列，因为编码孔径的像素为六边形，焦平面的像素为矩形，编码孔径与焦平面之间存在几何位错，几何位错产生了数学等价的矩形灰度编码孔径，增加了调制的自由度，提高了重建质量；同时采用蓝噪声编码孔径，使采样均匀，提高了高光谱三维数据的重建质量。

其次，在快照次数相同的情况下，六边形蓝噪声编码孔径的重建质量要比正方形蓝噪声重建质量高，正方形蓝噪声编码孔径的重建质量要比正方形随机编码孔径重建质量高。

再次，通过改变编码孔径与焦平面之间的几何位错量提高高光谱三维数据的重建质量。

附图说明

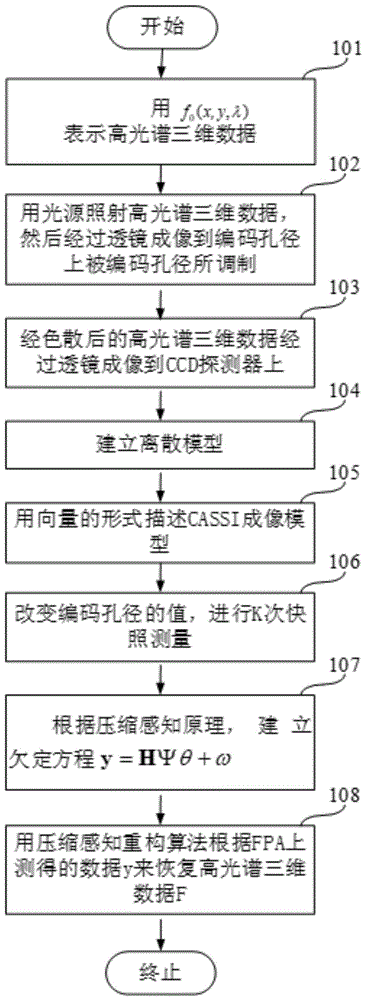
图1为本发明设计异形蓝色噪声编码孔径cassi系统的流程图。

图2为本发明应用的cassi系统结构图。

图3为本发明涉及的正方形像素和六边形编码孔径的周期性对应关系。

图4为在快照次数相同的情况下，六边形蓝噪声编码孔径，正方形蓝噪声编码孔径，正方形随机编码孔径重建结果的对比。

图5为几种编码孔径获得的重建光谱图像的平均snrs比较。

图6为随着编码孔径与焦平面之间的几何位错量的改变，六边形蓝噪声编码孔径重建结果snr改变的曲线图。

具体实施方式

下面结合附图进一步对本发明进行详细说明。

本发明的原理：在成像过程中，高光谱数据立方体在空间域x,y方向由异形蓝色噪声编码孔径调制，所提出的编码孔径是以六边形像素代替正方形，形成蜂窝状阵列，因为编码孔径的像素为六边形，焦平面的像素为矩形，编码孔径与焦平面之间存在几何位错，几何位错产生了数学等价的矩形灰度编码孔径，增加了调制的自由度，提高了重建质量。

如图1所示，一种采用异形蓝噪声编码孔径的光谱成像方法，具体步骤为：

步骤101、如图2cassi系统结构图所示，利用不同波长的光源照射待成像目标得到高光谱三维数据，用f0(x,y,λ)表示高光谱三维数据，其中x和y为空间坐标，λ是波长。

步骤102、高光谱三维数据经过透镜成像到编码孔径上被编码孔径所调制，用t(x,y)表示蓝噪声六边形编码孔径所等效的矩形灰度编码孔径在坐标(x,y)处的透过率，经过编码的高光谱三维数据然后被色散棱镜在x方向上所色散，经色散后的三维数据可表示为f1(x,y,λ)＝∫∫t(x,y)f0(x,y,λ)h(x′-αλ-x,y′-y)dx′dy′，其中h(x′-αλ-x,′y-y是)cassi系统的响应函数，α是色散棱镜的色散率。

步骤103、经色散后的高光谱三维数据经过透镜成像到ccd探测器上。

步骤104、为了简化步骤102中的公式，建立离散模型，高光谱三维数据用fi,j,l来表示，其维度为n×m×l，其中i，j，l为正整数，i，j是空间坐标，l是λ方向上的坐标。假设第k次快照时编码孔径的透过率用表示，ccd第k次测量的数据用y^k表示，则y^k的第(x,y)的元素值可表示为：

步骤105、对ccd测量值y^k进行逐点列扫描，并将y^k转化为列向量y^k，对三维数据f进行逐点列扫描，并将f转化为列向量f，用矩阵h^k表示编码孔径和色散棱镜的作用，则一次测量的成像模型为y^k＝h^kf+ω^k。

本发明所述步骤105中蓝噪声六边形编码孔径所等效的矩形灰度编码孔径在坐标(x,y)处的透过率的具体计算方法为：

步骤201、根据论文“blue-andgreen-noisehalftoningmodels"中的方法，生成六边形蓝噪声编码孔径；

其中,k表示探测次数，t^k表示第k次探测蓝噪声六边形编码孔径所等效的矩形灰度编码孔径的透过率；diag(t^k)表示n²×n²的对角矩阵，t^k表示t^k的向量表示，0表示维度为n²×n²(l-1)的零矩阵，i表示n²×n²的单位矩阵，表示n²l×n²l的置换矩阵，其结构和下面的矩阵结构相似：

步骤202、如图3所示，为正方形像素和六边形编码孔径的周期性对应关系，光谱图像上的每个正方形像素将由三个相邻的六边形像素调制。这意味着一个正方形像素的透射率等于对应的六边形透射率的加权平均值。因此，在矩形坐标系中，六边形编码孔径在数学上等同于灰度正方形编码孔径。根据重叠模式，可以分为两种类型，在图一中，由虚线和实线包围的像素显示了类型一和类型二的实例。对于类型一(位于奇数列的孔径)，灰度正方形像素的值由三个相邻六边形像素所调制，第一个在左边，第二个在右上角，第三个在右下角。用tb和tg分别表示二值六边形编码孔径和与其等价的灰度正方形编码孔径，因此，tg的第(i，j)个像素可计算为：

对于类型二(位于偶数列的孔径)，灰度正方形像素的值由三个相邻六边形像素所调制，第一个在左上角，第二个在左下角，第三个在右边。用tb和tg分别表示二值六边形编码孔径和与其等价的灰度正方形编码孔径，因此，tg的第(i，j)个像素可计算为

步骤203、改变编码孔径与焦平面之间的几何位错量可改变tg(i，j)的值，从而改变重建结果。

步骤106、多次改变六边形蓝噪声编码孔径相对于探测器的平移量α，即改变编码孔径的值，进行k次快照测量，ccd上k次探测的值可用向量y＝[y¹,y²,...y^k]^t表示。多次测量的成像模型为y＝hf+ω，其中h＝[h^1t,h^2t,...h^kt]^t，ω为ccd多次测量的总噪声。

步骤107、由于高光谱三维数据在相邻波段之间相邻空域之见存在很高的相关性，因此，假设f在基ψ上稀疏，θ表示稀疏系数，根据压缩感知原理，y＝hf+ω可用欠定方程y＝hψθ+ω来表示。

步骤108、用压缩感知重构算法根据ccd上测得的数据来恢复高光谱三维数据。

本发明的实施实例：

图3为在快照次数相同，透过率为0.5的情况下，六边形蓝噪声编码孔径，正方形蓝噪声编码孔径，正方形随机编码孔径重建结果的对比。第一行为原始光谱图像，第二行为使用六边形蓝色噪声编码孔径的重建图像，第三行为使用正方形蓝色噪声编码孔径的重构图像。第四行为使用正方形随机编码孔径的重构图像。

图4为几种编码孔径获得的重建光谱图像的平均snrs比较，红色虚线星形曲线为六边形蓝噪声编码孔径重建结果的snr曲线，绿色虚线圆曲线为正方形蓝噪声编码孔径重建结果的snr曲线，蓝色虚线圆曲线为正方形随机编码孔径重建结果的snr曲线，其中编码孔径的透射率为50％

图5为随着编码孔径与焦平面之间的几何位错量的改变，六边形蓝噪声编码孔径重建结果snr改变的曲线图。

在成像过程中，高光谱数据立方体在空间域x,y方向由异形蓝色噪声编码孔径调制，所提出的编码孔径是以六边形像素代替正方形，形成蜂窝状阵列。六边形像素的值是根据蓝噪声赋值为0或1。六边形蓝噪声编码孔径可以很容易地通过光刻掩模来实现。经过六边形蓝噪声编码孔径编码的三维数据然后由色散元件进行色散，经过成像透镜投射到检测器(ccd)上。因为编码孔径的像素为六边形，焦平面的像素为矩形，编码孔径与焦平面之间存在几何位错。几何位错产生了数学等价的矩形灰度编码孔径，增加了调制的自由度，提高了重建质量。最后，应用迭代稀疏重建算法恢复原始的高光谱数据。

虽然结合了附图描述了本发明的具体实施方式，但是对于本领域技术人员来说，在不脱离本发明原理的前提下，还可以做出若干变形、替换和改进，这些也应视为属于本发明的保护范围。