基于数字地图的无人机静态和动态路径规划方法与流程

本发明涉及无人机路径规划技术领域，具体涉及一种基于数字地图的无人机静态和动态路径规划方法。

背景技术：

无人机(unmannedaerialvehicle，uav)全称为无人驾驶飞机，它通过接受无线电指令或者通过本身程序控制进行飞行。20世纪，第一架无人机研制成功，随后以靶机形式的无人机研制成功，随着时间的推移，多指令程序控制的侦查无人机以及多种复杂控制形式的无人机相继研发成功，在不同的领域发挥着各自的作用。当今社会科学技术快速发展，尤其在现代战场环境下军事装备无人化已经成为明显的趋势。随着航空飞行技术的不断完善，具有自主控制功能的无人机在战场上的军事价值越来越明显，因此在未来复杂战场上，无人机必将成为各国军事抗争力量的重要组成部分。

无人机要完成自主作战飞行，路径规划是首先需要解决的关键技术之一，以往通过人为手工规划的路线较为粗糙，无法实现切实有效的突防效果，因此有必要通过计算性能优良的算法实现无人机路径精细规划。无人机路径规划是寻找起止位置之间的最优路径，在路径规划过程中主要需要考虑如下几个方面：飞行路线长度、地形、自然天气环境、威胁因素等^[6]，在综合这些因素的前提下规划出合理路线保证其在执行任务过程中安全顺利。通常情况下无人机的飞行环境存在诸多不确定性因素，从而导致无法在起始阶段获得确切的全局飞行环境信息，因此传统的无人机静态全局路径规划无法达到目前无人机的实时作战要求。目前关于无人机动态路径规划一般是当遇到威胁时，选择绕过突发威胁然后再回到原始的静态规划路线上，这种处理方式不仅会增加路径重规划时间，还会加大路径代价，进而增大油耗，机动性能比较差。

近些年路径规划的研究重点主要放在基于几何学的无人机路径规划搜索算法上，主要分为随机搜索型算法和确定型搜索算法，其中，确定型搜索算法包括动态规划算法、d*算法、a*算法以及dijkstra算法，此类算法对路径搜索具有可预见性，对于模型的建立要求相对简单，便于求解问题的实现，但由于无人机的路径规划最终是要上升到三维空间，数据计算量比较大，使用确定型算法会出现组合爆炸情况，不利于求解路径规划问题，而随机搜索型算法在复杂的问题空间中具有较好的全局优化性能，并且其鲁棒性和并行性相比于确定型搜索算法具有明显的优势。但是，目前飞行环境越来越复杂，对无人机的飞行要求也越来越高，因此，进一步研究实现更加优秀的无人机路径规划算法完成快速精准的无人机路径规划，仍是一个具有挑战的课题。

技术实现要素：

针对现有技术存在的问题，本发明提供一种基于数字地图的无人机静态和动态路径规划方法，在静态情况下，能够快速规划出精确的全局航行轨迹；在飞行过程中遇到突发威胁，可以快速规避威胁，有效进行路径重规划保障无人机飞行安全。

为了实现上述目的，一种基于数字地图的无人机静态和动态路径规划方法，具体步骤如下：

步骤1：采用数字地图技术构建无人机飞行三维数字地图，具体过程为：

步骤1.1：根据三维数字地形上任一点在水平面的投影坐标(x，y)所对应的地形高程值，构建基准地形图；

所述构建基准地形的公式如下：

其中，z1(x，y)为三维数字地形上任一点在水平面的投影坐标(x，y)所对应的地形高程值，a1～a7均为常系数，用于控制基准地形的起伏状态；

步骤1.2：根据数字地图中点(x，y)处的高程值，构建山峰地形图；

所述构建山峰地形的公式如下：

其中，z2(x，y)为数字地图中点(x，y)处的高程值，n为数字地图中山峰的个数，hm为第m个模拟山峰的高度，(xm，ym)为第m个模拟山峰的中心坐标，xsm为第m个模拟山峰在x轴方向的衰减量，ysm为第m个模拟山峰在y轴方向的衰减量；

步骤1.3：采用信息融合的思想将雷达工作区域等效为半球体地形处理，建立雷达威胁模型；

所述建立雷达威胁模型的公式如下：

其中，z3(x，y)为雷达威胁模型中点(x，y)处的雷达威胁等效高程值，(x3，y3，z3)为三维数字地形上任一点的位置坐标，r3为雷达威胁范围的半径；

步骤1.4：使用立方体模拟城市建筑物，建立城市环境模型；

所述城市环境模型的公式如下：

其中，z4(x，y)为城市建筑模型中点(x，y)处的高程值，(x4，y4)为城市环境模型中心坐标，length为城市环境模型中建筑物的横向长度，width为城市环境模型中建筑物的纵向宽度，h为城市环境模型中建筑物的高度；

步骤1.5：使用圆柱体模拟天气威胁，建立天气威胁模型；

所述天气威胁模型的公式如下：

其中，z5(x，y)为天气威胁模型中点(x，y)处的高程值，r5为天气威胁范围的半径，(x5，y5)为气象威胁中心坐标，hw为天气威胁模型的高度；

步骤1.6：将建立的基准地形图、山峰地形图、雷达威胁模型、城市环境模型和天气威胁模型转化为计算机能够处理的数据，结合信息融合的原理进行融合，形成综合数字地形信息等效三维数字地图；

所述综合数字地形信息等效三维数字地图的表达式如下：

z(x，y)＝max[z1(x，y)+z2(x，y)+z3(x，y)+z4(x，y)+z5(x，y)]；

其中，z(x，y)为综合数字地形信息等效三维数字地图中点(x，y)处的高程值；

步骤2：导入等效三维数字地图，设置无人机飞行的起始、终止位置坐标，初始化无人机路径规划约束条件，进行全局静态路径规划；

所述无人机路径规划约束条件包括最小飞行步长lmin；最大转弯角θ、最大爬升角度β、最低飞行高度hmin；

步骤3：初始化混合粒子群模拟退火算法参数，并对第i个粒子的位置xi和速度vi进行随机初始化，更新第i个粒子的速度vi和位置xi；

步骤3.1：初始化混合粒子群模拟退火算法参数，包括最大迭代次数tmax1、种群规模n、较高初温t、衰减因子α、学习因子c1和c2，并对第i个粒子的位置xi和速度vi进行随机初始化；

步骤3.2：根据无人机综合路径评价函数计算第i个粒子的适应度值f(xi)，并通过粒子最小适应度值确定粒子个体极值pbest和全局极值gbest；

所述无人机综合路径评价函数的公式如下：

其中，c为路径规划目标函数，l为路径长度，∑δw(s)为无人机飞行综合代价，所述无人机飞行综合代价∑δw(s)的公式如下：

∑δw(s)＝δowo(s)+δtwt(s)+δrwr(s)+δdwd(s)；

其中，wo(s)为无人机的耗油代价，wt(s)为飞行区域自然天气威胁代价，wr(s)为无人机受到的雷达威胁代价，wd(s)为地形威胁代价，δo为耗油代价权重系数，δt为天气威胁代价权重系数，δr为雷达威胁代价权重系数，δd为地形威胁代价权重系数，且δo+δt+δr+δd＝1；

步骤3.3：采用带压缩因子的方式对第i个粒子的速度vi和位置xi进行更新，得到更新后的第i个粒子的速度vi′和位置xi′；

所述更新后的第i个粒子的速度vi′和位置xi′的公式如下：

vi′＝χ[vi+c1r1(pbest-xi)+c2r2(gbest-xi)]；

xi′＝xi+vi′；

其中，r1和r2均为在[0，1]上的随机数，

步骤3.4：根据更新后的第i个粒子的速度vi′和位置xi′，计算第i个粒子更新后的适应度值f(xi′)，并计算更新前后第i个粒子适应度值的变量δf；

步骤3.5：判断第i个粒子适应度值的变量δf是否大于0，若是，则继续步骤3.6，若否，则接受更新后的第i个粒子的速度vi′和位置xi′，继续步骤4；

步骤3.6：判断exp(-δf/t)是否大于随机数rand(0，1)，若是，则接受更新后的第i个粒子的速度vi′和位置xi′，并根据第i个粒子更新后的适应度值f(xi′)更新粒子个体极值pbest和全局极值gbest，继续步骤4，若否，则不更新第i个粒子的速度vi和位置xi，继续步骤4；

步骤4：执行退火操作，令温度t＝αt，其中，α为衰减因子；

步骤5：判断混合粒子群模拟退火算法的当前迭代次数是否大于最大迭代次数tmax1，若是，则通过样条函数插值处理后绘出无人机全局静态最优飞行路径，若否，则输出粒子个体极值pbest和全局极值gbest，返回步骤3.2；

步骤6：初始化混合粒子群人工鱼群算法参数，包括线性递减惯性权重的最小值ωmin和最大值ωmax、粒子种群n、粒子视野visual、状态改变步长step、粒子群拥挤度因子δ、随机重复尝试次数try_number、最大迭代次数tmax2；

步骤7：判断无人机是否遇到突发威胁若是，则通过公告牌更新信息对下一代粒子进行更新，重新规划无人机飞行路径，若否，则根据无人机全局静态最优飞行路径飞行；

步骤8：判断混合粒子群人工鱼群算法的当前迭代次数是否大于最大迭代次数tmax2，若是，则通过样条函数插值处理绘出无人机全局动态最优飞行路径；若否，则返回步骤7。

进一步地，所述步骤7中通过公告牌更新信息对下一代粒子进行更新的步骤如下：

步骤s1：对第i个粒子的速度vi和位置xi进行更新，并计算更新后第i个粒子的适应度值f(xi′)，取适应度最小粒子状态及其值赋予给公告牌；

步骤s2：分别对粒子进行觅食、追尾、聚群以及随机行为；

步骤s2.1：设置第i个粒子的当前状态为在其视野范围内随机搜索到的下一个位置为种群最优中心状态为最优粒子状态为

步骤s2.2：判断第i个粒子第t代当前状态的综合路径评价函数值是否大于其视野范围内随机搜索到下一个位置的综合路径评价函数若是，则根据在第i个粒子第t代的视野范围内随机搜索到的下一个状态和在第t代内的全局极值点更新第i个粒子，得到第i个粒子第t+1代的速度v^t+1id和状态x^t+1id，继续步骤s3，若否，则不更新第i个粒子，继续步骤s2.3；

所述根据在第i个粒子第t代的视野范围内随机搜索到的下一个位置和在第t代内的全局极值点更新第i个粒子，得到第i个粒子第t+1代的速度和状态的公式如下：

其中，为在觅食行为下第i个粒子第t+1代的速度，t为当前迭代次数，tmax2为最大迭代次数，r1和r2均为在[0，1]上的随机数，为在觅食行为下第i个粒子第t+1代的当前状态，为随机行为；

步骤s2.3：判断在第i个粒子第t代的视野范围内随机搜索次数是否大于随机重复尝试次数try_number，若是，则粒子在其视野范围随机飞行，若否，则在第i个粒子第t代的视野范围内随机搜索下一个位置，返回步骤s2.2；

步骤s2.4：判断种群状态是否满足拥挤条件，若是，则返回步骤s2.2，若否，则根据在第i个粒子第t代的视野范围内搜索到的种群最优中心位置和在第t代内的全局极值点更新第i个粒子，得到第i个粒子第t+1代的速度和状态继续步骤s3；

所述根据在第i个粒子第t代的视野范围内搜索到的种群最优中心位置和在第t代内的全局极值点进行更新第i个粒子第t+1代的速度和状态的公式如下：

其中，为在聚群行为下第i个粒子第t+1代的速度，为在聚群行为下第i个粒子第t+1代的当前状态，nf为第i个粒子第t代的视野范围内其余人工鱼的鱼群数目；

步骤s2.5：判断第i个粒子当前状态的综合路径评价函数值是否小于最优粒子状态的综合路径评价函数值若是，则返回步骤s2.2，若否，则根据搜索到的最优粒子状态和在当前迭代状态下的全局极值点更新第i个粒子，得到第i个粒子第t+1代的速度v^t+1id和状态x^t+1id，继续步骤s3；

所述根据搜索到的最优粒子状态和在当前迭代状态下的全局极值点更新第i个粒子第t+1代的速度v^t+1id和状态x^t+1id的公式如下：

其中，为在追尾行为下第i个粒子第t+1代的速度，为在追尾行为下第i个粒子第t+1代的当前状态；

步骤s3：根据第i个粒子从第t代到第t+1代的更新过程计算第i个粒子第t+1代的适应度，选取个体行为中适应度最小值对应的第i个粒子第t+1代的速度v^t+1id和状态x^t+1id对第i个粒子的当前状态进行更新；

步骤s4：判断更新后第i个粒子的适应度是否小于公告牌中粒子的适应度，若是，则更新公告牌中的粒子状态信息进行，若否，则不更新公告牌中的粒子状态信息。

本发明的有益效果：

本发明提出一种基于数字地图的无人机静态和动态路径规划方法，在静态情况下，采用混合粒子群模拟退火算法(pso-sa算法)，该算法使用模拟退火突跳概率策略对粒子群算法进行优化，可以克服其早熟(局部极值)问题，并且可以快速规划出精准有效的无人机路线。在动态情况下，采用躲避威胁动态路径重规划的策略，从威胁点进行重新路径规划，为了提高算法在三维突发情况下的计算效率，采用混合粒子群人工鱼群算法(pso-afsa算法)，该算法引入人工鱼群的觅食、追尾、聚群等策略使粒子做出更优选择，该算法具有较好的全局收敛性能，可避免陷入局部极值，快速躲避威胁，进行精准路径重规划，降低无人机飞行的总代价。

附图说明

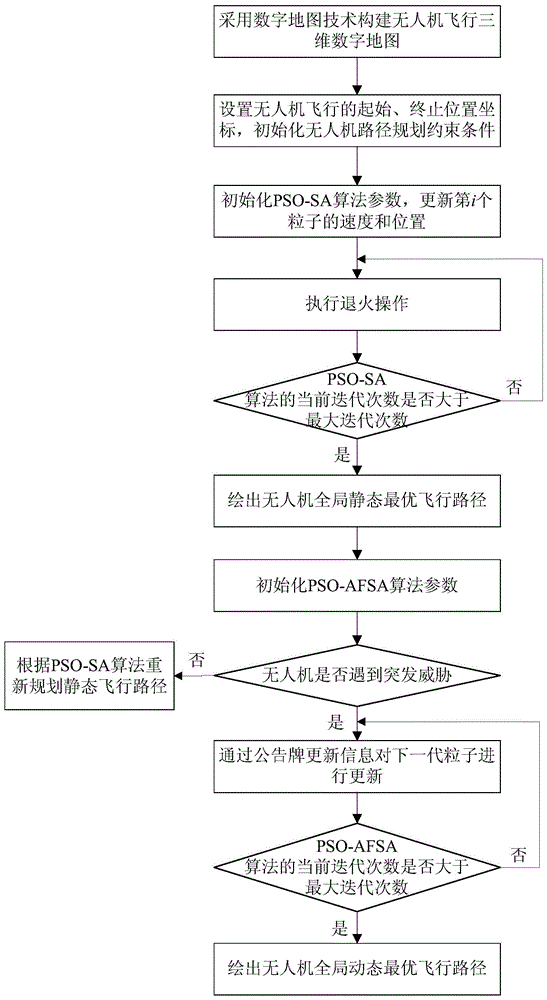
图1为本发明实施例中基于数字地图的无人机静态和动态路径规划方法的流程图；

图2为本发明实施例中数字地图基准地形图；

图3为本发明实施例中数字地图山峰地形图；

图4为本发明实施例中数字地图雷达模型图；

图5为本发明实施例中数字地图城市模型示意图；

图6为本发明实施例中数字地图天气威胁模型示意图；

图7为本发明实施例中综合数字地形信息等效三维数字地图；

图8为本发明实施例中在三维数字地图下使用本发明方法的路径规划图；

图9为本发明实施例中在同一个三维数字地图环境下，不同算法的路径规划俯视图；

其中，(a)为本发明提出算法的路径规划俯视图；(b)为afsa算法的路径规划俯视图；(c)为pso算法的路径规划俯视图。

具体实施方式

为了使本发明的目的、技术方案及优势更加清晰，下面结合附图和具体实施例对本发明做进一步详细说明。此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。

基于三维数字地图，本实施例提供一种基于数字地图的无人机静态和动态路径规划方法，在静态情况下，首先通过数字地图技术构建无人机飞行三维环境，设定飞行起始位置，然后使用通过引入sa突跳概率策略的pso-sa算法进行路径规划，通过无人机飞行约束条件确定飞行代价，在满足算法结束条件的基础上绘出无人机全局静态飞行路线；之后在数字地图上设定动态威胁，使用pso-afsa算法从威胁点位置进行精准路径重规划，降低无人机飞行的总代价。具体流程如图1所示，包括如下步骤：

步骤1：采用数字地图技术构建无人机飞行三维数字地图，具体过程为：

步骤1.1：根据三维数字地形上任一点在水平面的投影坐标(x，y)所对应的地形高程值，构建基准地形图。

所述构建基准地形的公式如式(1)所示：

其中，z1(x，y)为三维数字地形上任一点在水平面的投影坐标(x，y)所对应的地形高程值，a1～a7均为常系数，用于控制基准地形的起伏状态。

本实施例中，构建的基准地形如图2所示，在图2中显示了当a1到a7取值依次为10、0.2、0.1、0.6、1、0.1、0.1时的基准地形情况。

步骤1.2：根据数字地图中点(x，y)处的高程值，构建山峰地形图。

所述构建山峰地形的公式如式(2)所示：

其中，z2(x，y)为数字地图中点(x，y)处的高程值，n为数字地图中山峰的个数，hm为第m个模拟山峰的高度，(xm，ym)为第m个模拟山峰的中心坐标，xsm为第m个模拟山峰在x轴方向的衰减量，ysm为第m个模拟山峰在y轴方向的衰减量。

本实施例中，可以通过xsm和ysm来改变山峰表面的坡度。构建的山峰地形如图3所示，在图3中显示了当n＝4、h＝[20，35，25，20]，xm＝[20，70，20，80]，ym＝[30，20，70，80]，xsm＝[10，15，10，15]；ysm＝[10，15，10，10]时的山峰模型。

步骤1.3：采用信息融合的思想将雷达工作区域等效为半球体地形处理，建立雷达威胁模型。

所述建立雷达威胁模型的公式如式(3)所示：

其中，z3(x，y)为雷达威胁模型中点(x，y)处的雷达威胁等效高程值，(x3，y3，z3)为三维数字地形上任一点的位置坐标，r3为雷达威胁范围的半径。

本实施例中，建立的雷达威胁模型如图4所示。

步骤1.4：使用立方体模拟城市建筑物，建立城市环境模型。

所述城市环境模型的公式如式(4)所示：

其中，z4(x，y)为城市建筑模型中点(x，y)处的高程值，(x4，y4)为城市环境模型中心坐标，length为城市环境模型中建筑物的横向长度，width为城市环境模型中建筑物的纵向宽度，h为城市环境模型中建筑物的高度。

本实施例中，建立的城市环境模型如图5所示，无人机根据飞行中的位置可以选择横向绕过或者纵向越过城市环境模型。

步骤1.5：使用圆柱体模拟天气威胁，建立天气威胁模型。

所述天气威胁模型的公式如式(5)所示：

其中，z5(x，y)为天气威胁模型中点(x，y)处的高程值，r5为天气威胁范围的半径，即无人机距离天气威胁中心的距离，(x5，y5)为气象威胁中心坐标，hw为天气威胁模型的高度。

本实施例中，天气威胁指的是自然界存在的恶劣天气现象，如龙卷风、沙尘暴等，建立的天气威胁模型如图6所示，无人机根据飞行中的位置一般都会选择绕过天气威胁模型。

步骤1.6：将建立的基准地形图、山峰地形图、雷达威胁模型、城市环境模型和天气威胁模型转化为计算机能够处理的数据，结合信息融合的原理进行融合，形成综合数字地形信息等效三维数字地图。

所述综合数字地形信息等效三维数字地图的表达式如式(6)所示：

z(x，y)＝max[z1(x，y)+z2(x，y)+z3(x，y)+z4(x，y)+z5(x，y)](6)

其中，z(x，y)为综合数字地形信息等效三维数字地图中点(x，y)处的高程值。

本实施例中，形成的综合数字地形信息等效三维数字地图如图7所示，其中，山峰个数n＝8，山峰中心坐标分别为(5，85)，(20，180)，(25，25)，(45，165)，(50，85)，(65，65)，(85，145)，(130，50)；雷达个数1个，雷达中心坐标为(180，140)，半径为40；城市模型1个，城市模型中心坐标为(60，60)；天气威胁模型1个，模型中心坐标为(120，30)，半径为30；任务规划区域为200km×200km×0.4km，以1000∶1的比例将规划水平区域转换为200×200的坐标区域，其中，垂直方向采用1∶1的比例，即垂直方向最大坐标值表示400m。

步骤2：导入等效三维数字地图，设置无人机飞行的起始、终止位置坐标，初始化无人机路径规划约束条件，进行全局静态路径规划。

所述无人机路径规划约束条件包括最小飞行步长lmin；最大转弯角θ、最大爬升角度β、最低飞行高度hmin。

本实施例中，初始化无人机路径规划约束条件：最小飞行步长lmin＝1、最大转弯角θ＝45°、最大爬升角度β＝30°、最低飞行高度hmin＝1。

步骤3：初始化混合粒子群模拟退火算法参数，并对第i个粒子的位置xi和速度vi进行随机初始化，更新第i个粒子的速度vi和位置xi。

步骤3.1：初始化混合粒子群模拟退火算法参数，包括最大迭代次数tmax1、种群规模n、较高初温t、衰减因子α、学习因子c1和c2，并对第i个粒子的位置xi和速度vi进行随机初始化。

本实施例中，初始化pso-sa算法群体规模为100，退火参数为α＝0.98，初始温度10000，学习因子设为c1＝c2＝[1.8，2.2]；最大迭代次数tmax1＝100。

步骤3.2：根据无人机综合路径评价函数计算第i个粒子的适应度值f(xi)，并通过粒子最小适应度值确定粒子个体极值pbest和全局极值gbest；

所述无人机综合路径评价函数的公式如式(7)所示：

其中，c为路径规划目标函数，l为路径长度，∑δw(s)为无人机飞行综合代价，所述无人机飞行综合代价∑δw(s)的公式如下：

∑δw(s)＝δowo(s)+δtwt(s)+δrwr(s)+δdwd(s)；

其中，wo(s)为无人机的耗油代价，wt(s)为飞行区域自然天气威胁代价，wr(s)为无人机受到的雷达威胁代价，wd(s)为地形威胁代价，δo为耗油代价权重系数，δt为天气威胁代价权重系数，δr为雷达威胁代价权重系数，δd为地形威胁代价权重系数，且δo+δt+δr+δd＝1。

本实施例中，无人机飞行过程中的的耗油代价wo(s)主要取决于飞行距离以及飞行速度，设无人机飞行路径上共有n个节点，那么无人机飞行航程距离如式(8)所示：

其中，li表示无人机路径第i个节点和第i+1个节点之间的距离，假设无人机飞行速度保持恒定，则无人机的油耗代价如式(9)所示：

其中，o表示单位长度油耗比例系数。

本实施例中，为了方便计算路径段li的威胁代价，将此路径段等分为三份，分别为i1，i2，i3，其中α*代表某种威胁的第α*个威胁，例如αt代表第αt个自然天气威胁点，αr代表第αr个雷达威胁，αd代表第αd个地形威胁点，表示无人机距离威胁点的距离。

将具有一定半径和高度的圆柱体等效处理为雷暴天气，假设dtmax表示雷暴影响区域的最大半径，dtmin表示无人机坠毁概率为1的地区，设无人机距雷暴威胁中心的距离为dt，则雷暴天气对无人机造成的损坏概率pt(dt)如式(10)所示：

由式(10)可知自然天气威胁点α*对于路径段li的威胁代价如式(11)所示：

假设对于路径段li存在nt个自然天气威胁点，那么此段受到的天气总威胁如式(12)所示：

那么整条无人机路径的自然天气威胁代价如式(13)所示：

本是实施例中，无人机在飞行过程中受到的地形威胁代价wd(s)主要包括一些山峰和高地等产生的威胁代价，使用立体的圆锥进行近似表示，无人机在飞行过程中所对应高度的山峰横截面是一个圆周，设相应圆周的半径为rd，无人机离地高度为h，山峰的最大高度为h，其坡度是θ，无人机距离山峰对称轴的距离是dd，当h＞h时，不需要考虑地形威胁。设ddmin为允许无人机距离山峰地形的最近距离，当无人机距离山峰距离小于ddmin时，认为无人机撞毁的概率为1，相应的，当无人机距离山峰大于ddmax时，无人机无碰撞威胁。地形的仰角(坡度)θ计算公式如式(13)所示：

无人机在飞行过程中对应山峰横截面相应圆周的半径计算公式如式(14)所示：

rd(h)＝(h-h)/tanθ(14)

通过以上分析可得，无人机的碰撞概率如式(15)所示：

根据式(15)可知地形威胁αt对于路径段li的威胁代价如式(16)所示：

假设在路径段li上存在nd个地形威胁点，那么此段的地形威胁总代价如式(17)所示：

那么整条无人机路径的地形如式(18)所示：

雷达是在现实环境下比较常见的探测型威胁，具有远距离探测、识别和跟踪目标的功能，通过接收自身发射的电磁波回波进行分析，从而得到有关被探测目标的位置及方向等信息，因此，本实施例中考虑了无人机飞行过程中受到的雷达威胁代价。雷达是防空领域重量级设备，其电磁波信号满足如下信噪比公式(19)：

其中，pt为雷达发射功率，gr为接收天线增益，gt为发射天线增益，σ为有效探测截面面积，λ为信号工作波长，k为玻尔兹曼常数，lm为能量损耗因子，bn为滤波器匹配带宽，ts为绝对温度值，dr为无人机距离雷达中心的长度，通常情况下gr＝gt。为了方便分析，将式(19)整理可得式(20)：

其中，σ和r为变量，再将其余系统参数数值带入式(20)整理可得式(21)：

在现实环境下，对于给定无人机的散射截面面积是固定的，即σ为一常数值，那么式(21)可以进一步简化为式(22)：

其中，kr为一常数值。本实施例中，假设雷达的扫描范围为360°，其工作范围可以等效为一个半球体，设drmax为雷达可探测最大区域半径，drmin为雷达必然会探测到的地方，根据式(22)可知当无人机距离雷达中心o距离为dr时，无人机受到的探测威胁概率pr(dr)可近似为式(23)：

然后再通过粒子最小适应度值确定粒子个体极值pbest和全局极值gbest。

步骤3.3：采用带压缩因子的方式对第i个粒子的速度vi和位置xi进行更新，得到更新后的第i个粒子的速度vi′和位置xi′。

所述更新后的第i个粒子的速度vi′和位置xi′的公式如式(24)和式(25)所示：

vi′＝χ[vi+c1r1(pbest-xi)+c2r2(gbest-xi)](24)

xi′＝xi+vi′(25)

其中，r1和r2均为在[0，1]上的随机数，

步骤3.4：根据更新后的第i个粒子的速度vi′和位置xi′，计算第i个粒子更新后的适应度值f(xi′)，并计算更新前后第i个粒子适应度值的变量δf。

步骤3.5：判断第i个粒子适应度值的变量δf是否大于0，若是，则继续步骤3.6，若否，则接受更新后的第i个粒子的速度vi′和位置xi′，继续步骤4。

步骤3.6：判断exp(-δf/t)是否大于随机数rand(0，1)，若是，则接受更新后的第i个粒子的速度vi′和位置xi′，并根据第i个粒子更新后的适应度值f(xi′)更新粒子个体极值pbest和全局极值gbest，继续步骤4，若否，则不更新第i个粒子的速度vi和位置xi，继续步骤4。

步骤4：执行退火操作，令温度t＝αt，其中，α为衰减因子。

步骤5：判断混合粒子群模拟退火算法的当前迭代次数是否大于最大迭代次数tmax1，若是，则通过样条函数插值处理后绘出无人机全局静态最优飞行路径，若否，则输出粒子个体极值pbest和全局极值gbest，返回步骤3.2。

步骤6：初始化混合粒子群人工鱼群算法参数，包括线性递减惯性权重的最小值ωmin和最大值ωmax、粒子种群n、粒子视野visual、状态改变步长step、粒子群拥挤度因子δ、随机重复尝试次数try_number、最大迭代次数tmax2。

本实施例中，初始化pso-afsa算法参数，算法群体规模为100，最大迭代次数tmax2100，c1＝c2＝2，ω＝[0.4，0.9]，try_number＝50，visual＝20，δ＝0.618，step＝5。

步骤7：判断无人机是否遇到突发威胁，若是，则通过公告牌更新信息对下一代粒子进行更新，重新规划无人机飞行路径，若否，则无人机全局静态最优飞行路径飞行。

本实施例中，动态突发威胁路径重规划，在数字地图上设置突发威胁，设置突发威胁为气象威胁，其中心坐标为(160，130，0)，此威胁是无人机在飞行到该位置附近的时候探测到的。

所述通过公告牌更新信息对下一代粒子进行更新的步骤如下：

步骤s1：对第i个粒子的速度vi和位置xi进行更新，并计算更新后第i个粒子的适应度值f(xi′)，取适应度最小粒子状态及其值赋予给公告牌。

步骤s2：分别对粒子进行觅食、追尾、聚群以及随机行为。

步骤s2.1：设置第i个粒子的当前状态为在其视野范围内随机搜索到的下一个位置为种群最优中心状态为最优粒子状态为

步骤s2.2：判断第i个粒子第t代当前状态的综合路径评价函数值是否大于其视野范围内随机搜索到下一个位置的综合路径评价函数若是，则根据在第i个粒子第t代的视野范围内随机搜索到的下一个状态和在第t代内的全局极值点更新第i个粒子，得到第i个粒子第t+1代的速度v^t+1id和状态x^t+1id，继续步骤s3，若否，则不更新第i个粒子，继续步骤s2.3。

所述根据在第i个粒子第t代的视野范围内随机搜索到的下一个位置和在第t代内的全局极值点更新第i个粒子第t+1代的速度v^t+1id和状态x^t+1id的公式如式(26)和式(27)所示：

其中，为在觅食行为下第i个粒子第t+1代的速度，t为当前迭代次数，tmax2为最大迭代次数，r1和r2均为在[0，1]上的随机数，为在觅食行为下第i个粒子第t+1代的当前状态，为随机行为。

步骤s2.3：判断在第i个粒子第t代的视野范围内随机搜索次数是否大于随机重复尝试次数try_number，若是，则粒子在其视野范围随机飞行，若否，则在第i个粒子第t代的视野范围内随机搜索下一个位置，返回步骤s2.2；

步骤s2.4：判断种群状态是否满足拥挤条件，若是，则返回步骤s2.2，若否，则根据在第i个粒子第t代的视野范围内搜索到的种群最优中心位置和在第t代内的全局极值点更新第i个粒子，得到第i个粒子第t+1代的速度v^t+1id和状态x^+1tid，继续步骤s3。

所述判断种群状态是否满足拥挤条件的公式如式(28)所示：

其中，nf为第i个粒子第t代的视野范围内其余人工鱼的鱼群数目，若式(28)成立，则说明种群状态满足拥挤条件，否则不满足。

所述根据在第i个粒子第t代的视野范围内搜索到的种群最优中心位置和在第t代内的全局极值点进行更新第i个粒子第t+1代的速度v^t+1id和状态x^+1tid的公式如式(29)和式(30)所示：

其中，为在聚群行为下第i个粒子第t+1代的速度，为在聚群行为下第i个粒子第t+1代的当前状态。

步骤s2.5：判断第i个粒子当前状态的综合路径评价函数值是否小于最优粒子状态的综合路径评价函数值若是，则返回步骤s2.2，若否，则根据搜索到的最优粒子状态和在当前迭代状态下的全局极值点更新第i个粒子，得到第i个粒子第t+1代的速度v^t+1id和状态x^t+1id，继续步骤s3。

所述根据搜索到的最优粒子状态和在当前迭代状态下的全局极值点更新第i个粒子第t+1代的速度v^t+1id和状态x^t+1id的公式如式(31)和式(32)所示：

其中，为在追尾行为下第i个粒子第t+1代的速度，为在追尾行为下第i个粒子第t+1代的当前状态。

步骤s3：根据第i个粒子从第t代到第t+1代的更新过程计算第i个粒子第t+1代的适应度，选取个体行为中适应度最小值对应的第i个粒子第t+1代的速度v^t+1id和状态x^t+1id对第i个粒子的当前状态进行更新。

步骤s4：判断更新后第i个粒子的适应度是否小于公告牌中粒子的适应度，若是，则更新公告牌中的粒子状态信息，若否，则不更新公告牌中的粒子状态信息。

步骤8：判断混合粒子群人工鱼群算法的当前迭代次数是否大于最大迭代次数tmax2，若是，则通过样条函数插值处理绘出无人机全局动态最优飞行路径；若否，则返回步骤7。

本实施例中，通过采用pso-sa与pso-afsa算法进行路径规划的三维示意图如图8所示。采用粒子群算法(pso算法)、人工鱼群算法(afsa算法)以及本发明使用算法的无人机路径规划俯视图如图9所示，从图9中可以明显看出，本发明方法不仅可以完成路径规划任务，并且可以规划出精准简短安全的路线，规划效果明显优于pso和afsa算法。

最后应说明的是：以上实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解；其依然可以对前述实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；因而这些修改或者替换，并不使相应技术方案的本质脱离本发明权利要求所限定的范围。