一种基于泰勒展开的波动方程鬼波压制方法与流程

本发明涉及一种基于泰勒展开的波动方程鬼波压制方法，属于地震资料处理领域。

背景技术：

在海上拖缆地震资料采集过程中，拖缆一般置于海平面下一定深度，由于海平面的强反射，拖缆采集记录很强的虚反射，导致地震数据频谱发生陷波效应，极大地影响了数据品质，地震勘探一般将这种虚反射称为鬼波。鬼波一般不能很好的成像，会导致偏移剖面存在大量的偏移噪声。因此鬼波压制是海上地震勘探数据处理的一个关键环节。

近十年，为了有效压制鬼波获得宽频带地震资料，出现了一系列鬼波压制技术。这些技术通常可以分为两类：(1)和采集方式相关，上下源采集、上下缆采集、双检采集、拖缆三分量采集、海底电缆采集(obc)、变深度缆采集等，主要是通过特殊的采集方式再配合针对性的处理手段，实现鬼波的有效压制，拓宽地震资料的频带范围。这些特殊的采集方式受到野外作业条件的诸多限制，例如野外采集实施过程中震源、电缆的控制难度增加，从而引起采集费用的大幅度提升；(2)和处理技术相关，常用的方法是把鬼波压制看做一个反演问题，进行最小二乘求解。因为鬼波算子直接求逆存在奇异性问题，为了稳定求解，通常的做法是进行正则化约束，但是这种方法因为正则化项的引入，导致鬼波压制精度降低，压制后资料信噪比较低。

技术实现要素：

针对上述问题，本发明的目的是提供一种基于泰勒展开的波动方程鬼波压制方法，本发明方法可以实现鬼波的高精度压制，相比传统鬼波压制方法，本发明压制鬼波结果更保真，信噪比更高。

为实现上述目的，本发明采取以下技术方案：一种基于泰勒展开的波动方程鬼波压制方法，其包括以下步骤：

(1)将含有鬼波的地震数据表示为一次波和鬼波的叠加，得到由鬼波算子g表示的一次波表达式；

(2)将鬼波算子g基于泰勒展开，得到由波场延拓矩阵f表示的一次波表达式；

(3)计算得到波场延拓矩阵f，并将其代入步骤(2)中的一次波表达式，得到鬼波压制后的一次波。

进一步的，所述步骤(2)中，所述由波场延拓矩阵f表示的一次波表达式为：

p＝(1+f+f²+…)d，

其中，p为一次波，d为含鬼波的地震数据。

进一步的，所述步骤(3)中，计算得到波场延拓矩阵f的方法，包括以下步骤：

(3.1)将拖缆面γ0的记录波场p(r′)沿z轴向上延拓到海平面γ1，计算得到海平面γ1上r处的波场p(r)，该波场p(r)采用记录波场p(r′)及其法向导数的积分形式表示；

(3.2)设拖缆面和海平面之间的介质为均匀的，则近似得到拖缆面γ0的记录波场p(r′)的法向导数；

(3.3)在三维情况下对格林函数进行表示，得到格林函数的三维表达式；

(3.4)将步骤(3.2)和步骤(3.3)中得到的拖缆面γ0的记录波场p(r′)的法向导数以及格林函数的三维表达式代入步骤(3.1)中，得到不含法向导数的海平面上r处的波场p(r)的积分方程；

(3.5)将步骤(3.4)中的海平面上r处的波场p(r)积分方程进行离散化，即可得到波场延拓矩阵f。

进一步的，所述步骤(3.1)中，海平面γ1上r处的波场p(r)为：

其中，g(r,r′)是格林函数，表示法向导数。

进一步的，所述步骤(3.2)中，记录波场p(r′)的法向导数为：

其中，θ为边界法线方向和传播路径r-r′之间的夹角，为背景波数，c0为背景速度，ω为角频率。

进一步的，所述步骤(3.3)中，格林函数的三维表达式为：

进一步的，所述步骤(3.4)中，不含法向导数的海平面上r处的波场p(r)的积分方程为：

其中，r＝|r-r′|，

本发明由于采取以上技术方案，其具有以下优点：本发明采用基于泰勒展开的波动方程对含鬼波的地震数据进行表示，避免了直接对鬼波算子进行求逆时的奇异性问题，同时避免了常规方法中由于引入正则化项而导致的鬼波压制精度低，压制后资料信噪比较低的缺点，本发明计算简单，压制鬼波结果更保真，信噪比更高，可以广泛应用于鬼波压制技术领域。

附图说明

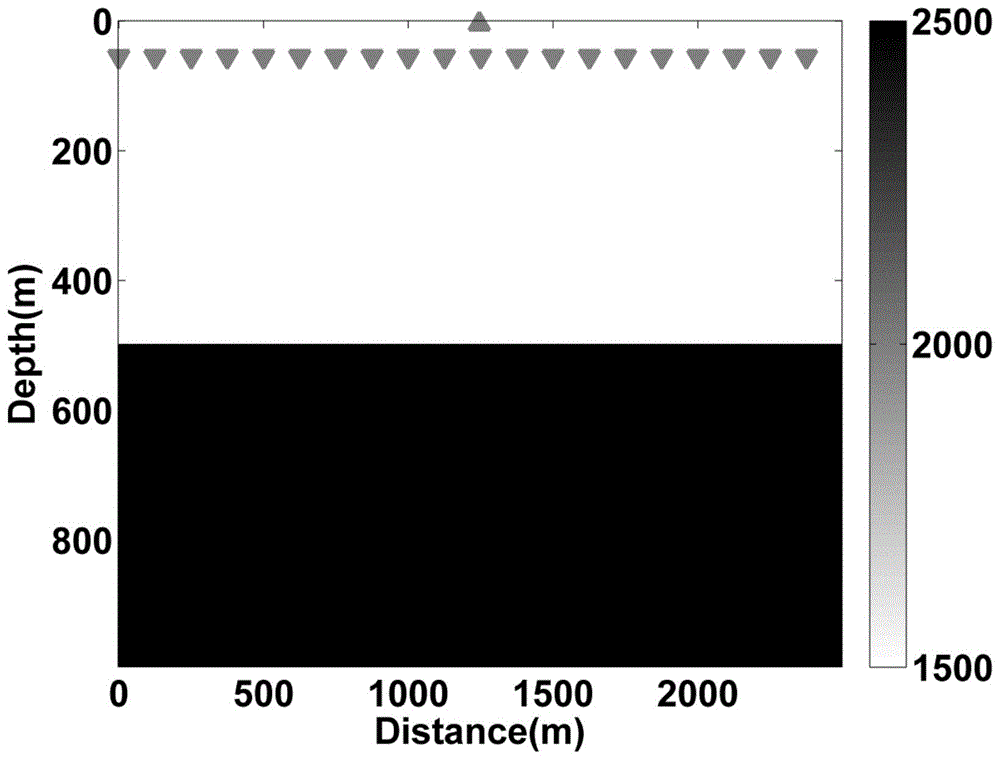
图1是速度模型，图中向上的三角表示震源，向下的三角表示检波器；

图2a是波动方程合成的含鬼波记录；

图2b是波动方程合成的不含鬼波记录(作为参考)；

图3a是采用常规方法压制鬼波结果；

图3b是采用本发明方法压制鬼波结果。

具体实施方式

下面结合附图和实施例对本发明进行详细的描述。

本发明提供的一种基于泰勒展开的波动方程鬼波压制方法，包括以下步骤：

(1)将含有鬼波的地震数据表示为一次波和鬼波的叠加，得到由鬼波算子g表示的一次波表达式。

带有鬼波的地震数据，可以视为一次波p和鬼波g的叠加，即

d＝p+g＝(i+rf)p＝gp(1)

其中，f表示波场延拓矩阵，r表示海平面的反射系数，通常假设等于-1，g表示鬼波算子。为了得到不含鬼波记录，需要对鬼波算子g进行求逆，直接对鬼波算子g求逆存在奇异性(分母为0)，通常的做法是在分母上加一个正则化项，即

其中，ε是一个小的正数。公式(2)是常规的鬼波压制算法，这种方法克服了奇异性问题，可以实现稳定的鬼波压制，但是因为公式(2)的算子并不完全等于鬼波算子的逆，因此鬼波压制精度较低。

(2)将鬼波算子g基于泰勒展开，得到由波场延拓矩阵f表示的一次波表达式。

由公式(1)可知，鬼波算子g＝(i-f)的逆1/(i-f),可以通过如下的泰勒展开来回避奇异性问题：

将公式(3)代入公式(1)，得到由波场延拓矩阵f表示的一次波p表达式：

p＝(1+f+f²+…)d(4)

可知，公式(4)是一种稳定的反演算子，其求解需要显式表征波场延拓矩阵f。

(3)计算得到波场延拓矩阵f，并将其代入步骤(2)中的一次波表达式，得到鬼波压制后的一次波。

具体的，包括以下步骤：

(3.1)将拖缆面γ0的记录波场p(r′)沿z轴向上延拓到海平面γ1，计算得到海平面γ1上r处的波场p(r)，其中，z轴表示深度方向，x轴和y轴表示水平方向。

波场p(r)采用记录波场p(r′)及其法向导数的积分形式表示，即：

其中，g(r,r′)是格林函数，表示法向导数。

(3.2)假设拖缆面和海平面之间的介质(即海水层)为均匀的，则可近似得到拖缆面γ0的记录波场p(r′)的法向导数。

为了计算r处的波场u(r)，需要知道拖缆面γ0的上波场u(r′)及其法向导数但是通常我们只记录波场值p(r′)，缺少法向导数的记录。为了利用方程(5)进行实际数据的波场延拓，需要对公式(5)进行简化。忽略拖缆面γ0与海平面γ1之间的多次反射，记录波场p(r′)的法向导数可以近似表示为：

其中，θ为边界法线方向和传播路径r-r′之间的夹角，为背景波数，c0为背景速度，ω为角频率。

(3.3)在三维情况下对格林函数进行表示，得到其计算式：

(3.4)将步骤(3.2)和步骤(3.3)中得到的拖缆面γ0的记录波场p(r′)的法向导数以及格林函数的三维表达式代入步骤(3.1)中，得到不含法向导数的海平面上r处的波场p(r)的积分方程：

其中，r＝|r-r′|，

(3.5)将步骤(3.4)中的海平面上r处的波场p(r)积分方程进行离散化，即可得到波场延拓矩阵f。

将波场p(r)积分方程进行离散化，得到：

p(r)＝fp(r′)(9)

结合公式(8)和(9)，即可得到波场延拓矩阵f。

下面结合具体实施例对本发明方法做进一步介绍。

1)波动方程正演模拟

如图1所示，是输入的半空间速度模型，其中方向向上的三角形表示震源，震源函数为主频15hz的雷克子波。检波器(图中方向向下的三角形)位于海平面下深度z＝50m位置。选取合适的参数进行正演模拟，可以得到如图2所示的地震记录，其中图2a表示含鬼波的地震记录，图2b表示不含鬼波的地震记录。从地震记录上可以清楚看到海面虚反射(鬼波)叠加在一次波之上。波动方程鬼波压制的目的是从图2a所示的含鬼波的地震记录中得到图2b所示的不含鬼波的地震记录。

2)基于公式(4)实现高精度鬼波压制

如图3a和图3b所示，分别采用本发明方法和常规方法(基于方程(2))对图2a所示的含鬼波的地震记录进行鬼波压制，其中，常规方法的鬼波压制结果如图3a所示,本发明方法的鬼波压制结果如图3b所示。通过与图2b进行对比，可以看出，本发明提出的波动方程鬼波压制方法可以进行高精度的鬼波压制，压制后的记录几乎和理想结果完全一致。从剖面上可以看出，常规算法可以恢复一次波，但是输出结果存在比较多的噪声，这是因为正则化项的引入带来的。

数值模拟实验的结果说明了本申请基于泰勒展开的波动方程鬼波压制技术的有效性和优越性。

上述各实施例仅用于说明本发明，其中各部件的结构、连接方式和制作工艺等都是可以有所变化的，凡是在本发明技术方案的基础上进行的等同变换和改进，均不应排除在本发明的保护范围之外。