一种梯度折射率火焰三维温度场测量方法与流程

本发明涉及一种梯度折射率火焰高精度三维温度场测量方法，属于测量技术领域。

背景技术：

在高温工业设备中，如锅炉、燃气轮机、发动机燃烧室等，为了提高燃烧效率和加强燃烧安全防护，通常需要实时监测各项燃烧参数。温度是高温热处理的重要热工参数，实时而准确的温度场检测是预防工业事故、高温测量、低碳环保、节约能源的重要手段。

图像法作为一种被动式非接触测量手段，在高温火焰的温度监测中得到了越来越多的关注，它需要建立火焰中的辐射传输模型。目前图像测温法通常假定介质的折射率均匀分布，即假定了光线的传播轨迹可以按直线处理，然而在实际生产中，火焰内部的温度分布不均会导致折射率分布不均。尤其是在大型火焰中，火焰内部存在多个高温区，如果不考虑由于折射率分布不均带来的光线偏折的影响，由此得到的温度测量结果会造成较大的误差。

折射率的测量方法通常有纹影法、光学干涉法、阴影法、全息干涉法等，而其中纹影法具有测量精度高、测量装置简单的优点，它是一种将相分布转换为可见图像的光学方法，通常可以用于测量一个区域内的介质折射率，然后根据折射率与温度的g-d关系式来测量火焰的温度场，但不同燃料和燃烧工况下的温度和折射率之间的这种状态关系是半经验的理论，只能针对少量工况有较好的测量精度。

技术实现要素：

本发明所要解决的技术问题是针对上述现有技术存在的问题，而提出一种基于纹影法与图像法的融合测试技术，旨在测量梯度折射率火焰的三维温度场，以解决传统火焰温度场计算模型因忽略火焰对光的折射作用而无法保证足够精度的问题。

本发明的技术方案如下：

一种梯度折射率火焰高精度三维温度场测量方法，包括以下几个步骤：

步骤一：利用同步控制器连接两台相机，对轴对称燃烧火焰实现同时采集其“z”字型纹影成像和火焰自发光灰度图像。

步骤二：根据纹影成像中光线经过火焰由于折射率引起的起偏角，获得火焰的折射率分布，偏转角θ和折射率n之间的关系：

其中x方向为光线入射方向，y方向为入射方向的垂直方向。

步骤三：根据火焰的折射率分布，利用菲涅尔折射定律，从相机的探测器逆向追踪光线，记录光线在火焰中的穿行方向和控制体编号。

步骤四：利用黑体炉在相同工作距离和曝光条件下标定图像灰度与温度之间的关系，获得火焰的出射辐射强度分布。

步骤五：根据光线在火焰中的传播路径，利用源项有限体积法建立火焰广义辐射源项和相机探测到的火焰出射辐射强度之间的关系：

其中，i(rw，ω)表示探测到的火焰出射辐射强度，s(r，ω)表示火焰广义辐射源项，β表示火焰的衰减系数，m表示光线在火焰中穿过的控制体总个数，δs表示火焰在每个控制体中穿行的距离，ω表示某根光线代表的探测方向。

步骤六：根据广义辐射源项和火焰出射辐射强度的关系，采用lsqr反演算法进行迭代计算，重建出火焰的三维辐射源项分布。

步骤七：将广义源项分布代入梯度折射率介质的辐射传递方程，利用直角坐标系下的有限体积法计算出梯度折射率火焰的辐射强度分布，直角坐标系下梯度折射率辐射传递方程形式为：

其中，i(r，ω)表示火焰在位置r沿方向ω的辐射强度大小，θ为极角，为方位角，ξ＝cosθ，ka为吸收系数，ks表示散射系数。

步骤八：根据广义源项的定义和辐射强度分布，计算出火焰的自发辐射强度，进而根据黑体发光或化学发光中温度与自发辐射强度之间的关系获得火焰的温度分布。广义辐射源项定义为：

其中，ib(r)表示火焰的自发辐射强度分布，i(r，ω′)表示火焰在位置r沿方向ω′的辐射强度大小φ(ω，ω′)表示由ω方向散射出去并且由ω′方向入射的散射相函。dω′表示立体角大小。

有益效果

与现有技术相比，本发明有以下优点：

1、考虑了火焰的折射率分布，建立了梯度折射率火焰的成像模型，比当前未考虑折射率影响的图像法温度测量方法，从模型上来说更加精确。

2、利用纹影法测量得到了火焰的折射率分布，没有进一步采用传统纹影法测温的折射率和温度场的关系或者温度场，而是与图像法测温相结合，避免了传统的纹影法测温时由于使用半经验公式而只能在少数工况下适用的范围限制。

3、由于采用纹影法与图像法相融合的测温方法，突破了原来纹影法测温中只考虑气体而忽略颗粒散射的特性，测温对象可以从原来的化学发光火焰拓展到黑体发光与化学发光共存的大部分火焰。

附图说明

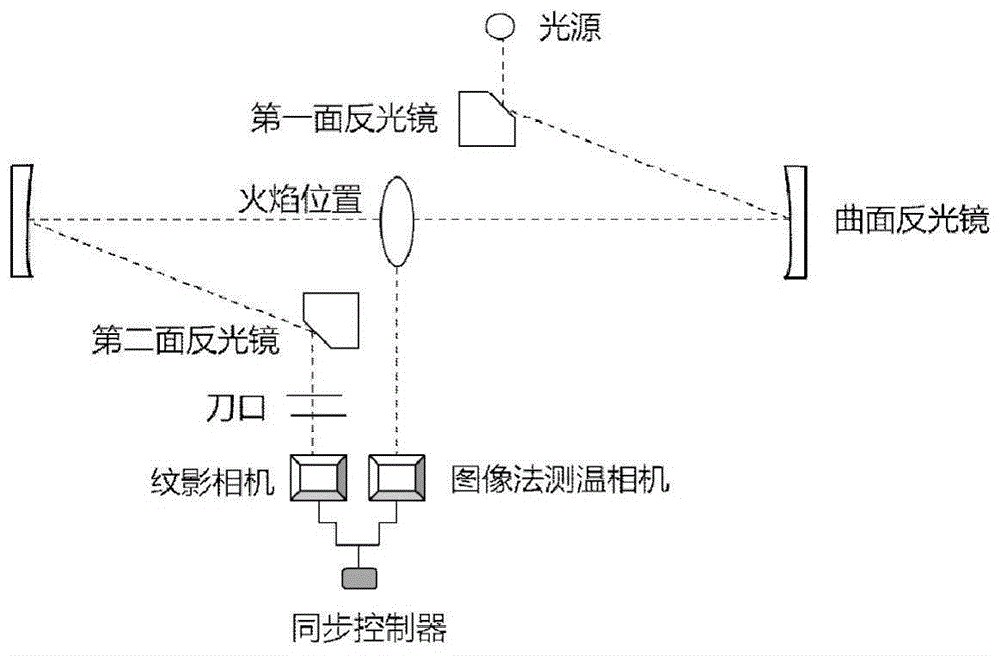
图1为实验系统示意图；

图2为采集的蜡烛火焰图像；

图3为采用纹影法得到的火焰纹影图；

图4为在某一控制体界面处的光线偏折示意图；

图5为光线在梯度折射率介质中的轨迹追踪示意图；

图6为黑体炉标定的灰度值与强度值的关系曲线图；

图7为考虑梯度折射率后的火焰温度场三维重建结果。

具体实施方式

下面结合附图，对本发明的具体实施方式作进一步详细描述。

具体包括以下几个步骤：

步骤一：搭建如图1所示的实验系统，首先利用同步控制器连接纹影相机以及图像法测温相机，然后对燃烧的蜡烛火焰实现同时采集其“z”字型纹影成像和火焰自发光灰度图像(如图2，图3所示)。

步骤二：根据纹影成像中光线经过火焰由于折射率引起的起偏角，根据偏转角θ和折射率n之间的关系，获得火焰的折射率分布，

其中，x方向为光线入射方向，y方向为入射方向的垂直方向。

步骤三：根据火焰的折射率分布，利用菲涅尔折射定律，从相机的探测器逆向追踪光线，记录光线在火焰中的穿行方向和控制体编号，菲涅尔折射定律为：

式中，j为控制体编号；

光线在其中某一个控制体界面的偏折如图4所示；而当用i(rw，ω)表示探测到的火焰出射辐射强度，δs表示火焰在每个控制体中穿行的距离时，光线整个的偏折轨迹如图5所示。

步骤四：打开黑体炉和相机，将相机与黑体炉的距离、曝光条件等参数调整到与采集火焰图像时相同，黑体炉温度从600℃到850℃，每隔50℃拍摄十张黑体炉图像，根据普朗克定律，通过拟合得到强度值与灰度值的关系，完成标定(如图6)，获得火焰的出射辐射强度分布。

步骤五：根据光线在火焰中的传播路径，利用源项有限体积法建立火焰广义辐射源项和相机探测到的火焰出射辐射强度之间的关系：

其中，i(rw，ω)表示探测到的火焰出射辐射强度，s(r，ω)表示火焰广义辐射源项，β表示火焰的衰减系数，m表示光线在火焰中穿过的控制体总个数，δs表示火焰在每个控制体中穿行的距离，ω表示某根光线代表的探测方向；i，j为控制体编号；

步骤六：在吸收系数已知的条件下，步骤五中的关系式可简化为如下形式：

ax＝b

其中，a，b均为常数矩阵，x为所求辐射源项分布矩阵。

接下来采用lsqr反演算法进行计算，通过初始化、变量迭代循环计算以及参数修正等步骤对该方程进行求解，最终求得火焰的三维辐射源项分布结果。

步骤七：将广义源项分布代入梯度折射率介质的辐射传递方程，利用直角坐标系下的有限体积法计算出梯度折射率火焰的辐射强度分布，直角坐标系下梯度折射率辐射传递方程形式为：

其中，i(r，ω)表示火焰在位置r沿方向ω的辐射强度大小，

式中，i，j和k均为粗体，表示三个垂直方向上的单位向量；θ为极角；为方位角；ξ＝cosθ；ka为吸收系数；ks表示散射系数。

步骤八：根据广义源项的定义和辐射强度分布，计算出火焰的自发辐射强度，进而根据黑体发光或化学发光中温度与自发辐射强度之间的关系获得火焰的温度分布(如图5所示)。广义辐射源项定义为：

其中，ib(r)表示火焰的自发辐射强度分布，i(r，ω′)表示火焰在位置r沿方向ω′的辐射强度大小φ(ω，ω′)表示由ω方向散射出去并且由ω′方向入射的散射相函；dω′表示立体角大小。

研究对象为黑体发光火焰时，辐射强度与温度的关系为：

式中，ibλ是波长λ的光谱辐射强度值，w/(sr·m³)；ε是黑体的发射率；t是黑体的温度值，k；c1为第一辐射常数，c2为第二辐射常数，分别为3.7418×10^-16w·m²和1.4388×10^-2m·k。

研究对象为化学发光火焰时，根据化学发光测温原理，分子中不同能级间的跃迁产生相应的谱线强度与温度的关系为：

式中，h为普朗克常数，c为光速，v为振动能级，j′为高能级转动量子数；n为高能级分子数，a为自发发射爱因斯坦跃迁概率，v为跃迁波数；n0为分子总数，k为玻尔兹曼常数，ge为电子态简并度，te、tv、tr分别为电子、振动和转动温度，ee、ev、er分别为电子态、振动态和转动态能量，qe、qv、qr分别为电子态、振动态和转动态配分函数。