一种基于磁传感器阵列的磁偶极子目标跟踪方法与流程

本公开涉及一种基于磁传感器阵列的磁偶极子目标跟踪方法。

背景技术：

随着海洋资源的持续开发，海域权益与临海安全性受到世界各国的广泛关注与重视，研究快速、高效的侵入目标检测与识别方法，对于提高临海防御能力具有重要军事意义。磁探测技术是一种被动探测技术，因其能够有效弥补声学近场、近海探测的不足受到国内外的广泛关注。通过传感器阵列采集感兴趣目标体周围的磁异常信号，以获取兴趣目标的电磁特征，进而实现目标的识别及快速定位和跟踪具有重要的研究价值。

磁目标的定位与跟踪最常用的方法包括两大类：优化定位算法与滤波算法。其中，优化定位算法通常建立在较多观测数据基础上，比如传感器网络、磁梯度张量系统或者航磁飞行测线等，通过最优化估计算法以获取目标位置、磁矩等特征参量。滤波跟踪算法，通常基于传感器阵列持续测量运动目标磁场数据，以实现对磁目标体的实时跟踪与状态估计，由于良好的跟踪性能于实时性等优点，受到国内外学者及研究人员的广泛关注。

但研究人员发现现有技术中存在以下问题：以往利用传感器阵列对磁偶极子目标跟踪的算法研究集中于优化算法的非线性模型适应能力，在抑制地磁干扰方面主要通过梯度系统完成。磁梯度系统虽然可以很好的抑制地磁干扰，但是受制于基线过短、磁梯度场衰减快等因素，磁梯度系统不适合与目标的远距离跟踪。

当磁偶极子目标接近磁传感器阵列时，传感器测量磁场中同时包含目标磁异常场与背景地磁场。现有技术一般通过设置远参考传感器方法，利用参考传感器与测量传感器间地磁场的空间相关性，消除测量磁场中的地磁背景，获取目标磁异常场，即通过在较远的位置设立参考传感器，参考传感器仅测量背景而其余的阵列传感器同时测量背景与目标的磁异常信号，这样通过处理以实现消除背景磁场而获得目标的磁异常信号之目的。然而，基于参考磁传感器的方法存在着两个明显的缺陷：其一，参考传感器与测量传感器之间距离难以把握，距离较近时，参考传感器容易受目标磁异常影响，致使测量磁异常产生误差；当二者距离较远时，传感器间的相关性下降，致使地磁背景场消除不彻底。其二，参考传感器的设置处需要可靠的地磁环境，以保证工作期间不受外界其他磁干扰源影响。此外，通过构建磁梯度张量系统也可以有效的避免地磁干扰，然而磁梯度场的衰减较磁偶极子场更快，并不适合远距离目标跟踪。

技术实现要素：

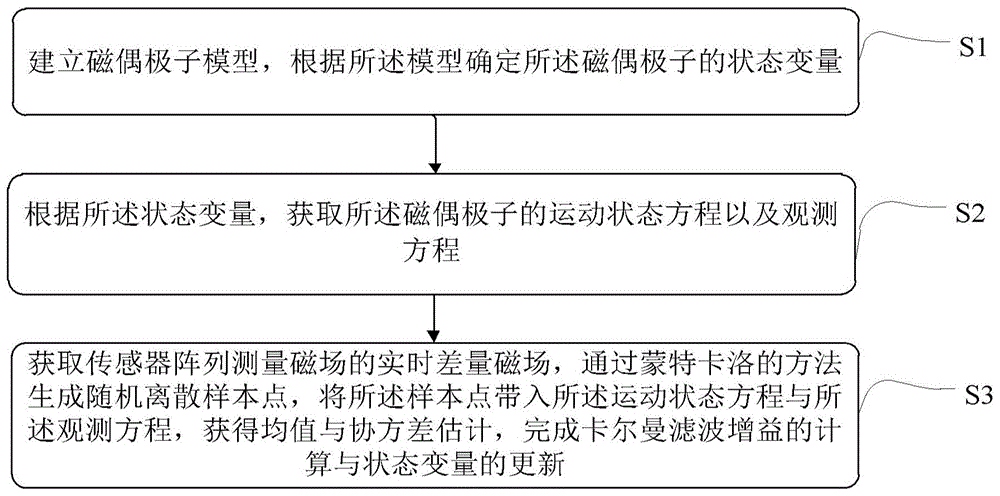
本公开提供了一种基于磁传感器阵列的磁偶极子目标跟踪方法，所述方法包括：步骤1，建立磁偶极子模型，根据所述模型确定所述磁偶极子的状态变量；步骤2，根据所述状态变量，获取所述磁偶极子的运动状态方程以及观测方程；步骤3，获取传感器阵列测量磁场的实时差量磁场，通过蒙特卡洛的方法生成随机离散样本点，将所述样本点带入所述运动状态方程与所述观测方程，获得均值与协方差估计，完成卡尔曼滤波增益的计算与状态变量的更新。

附图说明

为了更完整地理解本公开及其优势，现在将参考结合附图的以下描述，其中：

图1示意性示出了本公开实施例提供的基于磁传感器阵列的磁偶极子目标跟踪方法的方法流程图；

图2示意性示出了本公开实施例提供的基于磁传感器阵列的磁偶极子目标跟踪方法中步骤3的方法流程图；

图3示意性示出了本公开实施例提供的仿真示例中仿真磁偶极子运动轨迹图；

图4a示意性示出了本公开实施例提供仿真示例中仿真磁偶极子在x坐标轴投影的运动轨迹图；

图4b示意性示出了本公开实施例提供仿真示例中仿真磁偶极子在y坐标轴投影的运动轨迹图；

图4c示意性示出了本公开实施例提供仿真示例中仿真磁偶极子在z坐标轴投影的运动轨迹图；

图5a示意性示出了本公开实施例提供仿真示例中传感器1处的测量磁场三分量；

图5b示意性示出了本公开实施例提供仿真示例中传感器1处的磁梯度场中x分量磁场在x方向梯度、y分量场在y方向梯度及z分量场在z方向的梯度；

图5c示意性示出了本公开实施例提供仿真示例中传感器1，2的差量磁场；

图6示意性示出了本公开实施例1中磁偶极子的运动轨迹图；

图7a示意性示出了本公开实施例1中x坐标轴投影轨迹的误差；

图7b示意性示出了本公开实施例1中y坐标轴投影轨迹的误差；

图7c示意性示出了本公开实施例1中z坐标轴投影轨迹的误差；

图8示意性示出了本公开实施例提供的基于磁传感器阵列的磁偶极子目标跟踪系统的框图；

图9示意性示出了本公开实施例提供的基于磁传感器阵列的磁偶极子目标跟踪方法中步骤3的流程图。

具体实施方式

以下，将参照附图来描述本公开的实施例。但是应该理解，这些描述只是示例性的，而并非要限制本公开的范围。在下面的详细描述中，为便于解释，阐述了许多具体的细节以提供对本公开实施例的全面理解。然而，明显地，一个或多个实施例在没有这些具体细节的情况下也可以被实施。此外，在以下说明中，省略了对公知结构和技术的描述，以避免不必要地混淆本公开的概念。

在此使用的术语仅仅是为了描述具体实施例，而并非意在限制本公开。在此使用的术语“包括”、“包含”等表明了所述特征、步骤、操作和/或部件的存在，但是并不排除存在或添加一个或多个其他特征、步骤、操作或部件。

本公开的一个实施例提供了一种基于磁传感器阵列的磁偶极子目标跟踪方法，参见图1，所述方法包括步骤1～步骤3的内容：

步骤1，建立磁偶极子模型，根据所述模型确定所述磁偶极子的状态变量。

当磁性目标体的探测距离大于其自身尺寸的3倍时，目标体可等效为磁偶极子，磁偶极子矢量磁场表达式如下式。

式中，μ0为自由空间磁导率，m为目标体总磁矩矢量，r为目标与传感器之间的距离矢量，r为距离矢量r的幅度。

当坐标系确立后，磁偶极子矢量磁场可以写为如式1矩阵形式。

其中，x0，y0，z0为在三维坐标系中矢量磁力仪的坐标，x，y，z为在三维坐标系中磁偶极子的坐标；bx，by，bz为磁偶极子磁场矢量在三维坐标轴的投影分量，而mx，my，mz代表了磁偶极子磁矩矢量在三维坐标坐标轴的投影分量，r为磁偶极子与传感器之间的距离矢量的幅度，μ0为自由空间磁导率。对于任意磁偶极子目标产生的磁场唯一依赖于目标与传感器的相对位置及磁偶极子的磁矩。通过独立的六个变量确定。

当传感器在地磁环境中进行测量时，测量磁场可以表示为磁偶极子异常磁场与背景地磁场的叠加形式如下式。

bm＝b+be(13)

其中，bm，b，be分别代表传感器处的总磁场、目标磁异常场和地磁场矢量。

步骤2，根据所述状态变量，获取所述磁偶极子的运动状态方程以及观测方程。

根据磁偶极子模型，在目标的跟踪过程中目标的状态变量由两个部分组成：描述目标运动状态的位置参数与速度参数；描述目标磁性的磁矩参数。因此在时间t时刻，所述状态变量通过下列状态变量的向量表达式表示：

xt＝[x(t)，y(t)，z(t)，vx(t)，vy(t)，vz(t)，mx(t)，my(t)，mz(t)](2)

其中，x(t)，y(t)，z(t)分别表示t时刻磁偶极子在x方向，y方向和z方向的位置，vx(t)，vy(t)，vz(t)分别表示t时刻磁偶极子在x方向，y方向和z方向的速度，mx(t)，my(t)，mz(t)分别表示t时刻磁偶极子在x方向，y方向和z方向的磁矩。

考虑到实际水面舰船及水下航行器等目标运动相对缓慢，状态相对稳定等情况，可以用恒速模型来描述磁偶极子目标的运动状态，可以满足实际工作需求。描述目标运动的状态方程可以表达如下式14。

x(t)＝x(t-δt)+δt·vx(t-δt)

y(t)＝y(t-δt)+δt·vy(t-δt)

z(t)＝z(t-δt)+δt·vz(t-δt)

vx(t)＝vx(t-δt)(14)

vy(t)＝vy(t-δt)

vz(t)＝vz(t-δt)

对于目标的磁矩参量，当磁偶极子目标运动过程中姿态发生变化时磁矩也会发生相应的改变，考虑到磁偶极子姿态运动状态无法估计且短时间相对稳定等因素，可以用恒磁矩状态方程表示如下式15。

mx(t)＝mx(t-δt)

my(t)＝my(t-δt)(15)

mz(t)＝mz(t-δt)

根据目标的位置参量与磁矩参量，可以获得不同传感器位置处的磁异常场，当使用3个矢量磁场传感器测量磁场时，测量场可以表示为因此t时刻的观测输出量z，观测输出量即为传感器阵列在目标跟踪过程中实际观测的磁场值，可以表示如下式16。

zt＝[bx1(t)，by1(t)，bz1(t)，bx2(t)，by2(t)，bz2(t)，bx3(t)，by3(t)，bz3(t)](16)

其中，bx1(t)，by1(t)，bz1(t)分别表示第一传感器在x方向、y方向和z方向上的测量场，bx2(t)，by2(t)，bz2(t)分别表示第二传感器在x方向、y方向和z方向上的测量场，bx3(t)，by3(t)，bz3(t)分别表示第三传感器在x方向、y方向和z方向上的测量场。

综上可得，磁偶极子目标跟踪过程中的状态方程是线性的；而观测方程是非线性的。

步骤3，获取传感器阵列测量磁场的实时差量磁场，通过蒙特卡洛的方法生成随机离散样本点，将所述样本点带入所述运动状态方程与所述观测方程，获得均值与协方差估计，完成卡尔曼滤波增益的计算与状态变量的更新。

在一种可行的方式中，参见图2以及图9，所述步骤3可以通过下列步骤301-步骤305进行实现，步骤3的方法为蒙特卡洛卡尔曼滤波方法，具体地：

步骤301，对卡尔曼滤波器进行初始化设置，将所述状态变量及其协方差进行初始化。

定义初始状态变量x0为9×1维列向量；初始化协方差为9×9矩阵，

x0＝[x(0)，y(0)，z(0)，vx(0)，vy(0)，vz(0)，mx(0)，my(0)，mz(0)](3)

其中，x(0)，y(0)，z(0)为分别为磁偶极子在x方向，y方向和z方向的位置初始值；vx(0)，vy(0)，vz(0)为磁偶极子在x方向，y方向和z方向的速度初始值；mx(0)，my(0)，mz(0)为磁偶极子在x方向，y方向和z方向的磁矩初始值。

步骤302，根据蒙特卡洛方法随机生成n个样本点，根据所述样本点和所述磁偶极子的运动状态方程，获取状态变量均值预测，以及状态变量的协方差预测。

根据蒙特卡洛方法随机生成n个样本点，为i＝1，2，…，n，样本点权重wi＝1/n，i＝1，2，…，n；

获取n时刻的状态变量均值预测值xn|n-1为：

获取n时刻的状态变量的协方差预测值为：

其中，c(i)～n(c；0，i)，i＝1，2，…，n；xn-1/n-1为n-1时刻的状态变量均值，dn-1|n-1为n-1时刻的变量标准差，n＝2，3，4…；为所述磁偶极子的运动状态方程；q为状态转移过程中变量随机误差的协方差矩阵。

q值设定是考虑到状态变量的随机性分布，当q值估计偏大时会导致跟踪的误差的增加，而q值估计偏小时跟踪速度变慢以至于不能适应目标的随机性变化。本公开实施例中：q值为0.01*diag([1110.010.010.01111])；即假定变量位置x、y、z的随机分布标准差为0.1m，而速度vx、vy、vz变量的随机分布标准差为0.01m/s，磁矩mx、my、mz的随机分布标准差为0.1am²。

步骤303，根据蒙特卡洛方法随机生成n个样本点，根据所述样本点、所述磁偶极子的运动状态方程和观测方程，获取观测量均值预测、观测量协方差预测、观测量与状态变量的互协方差预测。

根据蒙特卡洛方法随机生成n个样本点，为i＝0，1，2，…，n，样本点权重wi＝1/n，i＝1，2，…，n；

获取n时刻的观测量均值预测值zn|n-1为：

获取n时刻的观测量协方差预测值为：

获取n时刻的观测量与状态变量的互协方差预测值为：

其中：其中，c(i)～n(c；0，i)，i＝1，2，…，n；dn-1|n-1为n-1时刻的变量标准差，xn-1/n-1为n-1时刻的状态变量均值，xn|n-1为n时刻的状态变量均值预测值；n＝2，3，4…；为所述磁偶极子的运动状态方程；为所述磁偶极子的观测方程；r测量噪声协方差矩阵。

测量噪声协方差矩阵r，由实际跟踪过程中采用的传感器噪声水平决定，在本公开实施例中：假设传感器的噪声水平为1e^-10(rms)，因此对应的观测协方差为r值为1e-²⁰*diag([111111])。

步骤304，通过所述观测量协方差预测、所述观测量与状态变量的互协方差预测，计算卡尔曼滤波增益估计；利用所述观测量均值预测、所述卡尔曼滤波增益估计与实时差量磁场，更新状态变量均值及其协方差矩阵。

所述卡尔曼滤波增益估计kn为：

所述n时刻的状态变量均值xn|n为：xn|n＝xn|n-1+kn(zn-zn|n-1)(10)

所述n时刻的协方差矩阵为：

其中，为n时刻的观测量协方差预测值，为n时刻的观测量与状态变量的互协方差预测值，xn|n-1为n时刻的状态变量均值预测值；zn|n-1为n时刻的观测量均值预测值，为n时刻的状态变量的协方差预测值；

zn为n时刻测量的差量磁场，可以通过下式进行表示：

zn＝[bx1(n)-bx2(n)，by1(n)-by2(n)，bz1(n)-bz2(n)，bx2(n)-bx3(n)，by2(n)-by3(n)，bz2(n)-bz3(n)]

其中，bx1(n)，by1(n)，bz1(n)分别表示n时刻第一传感器在x方向、y方向和z方向上的测量场，bx2(n)，by2(n)，bz2(n)分别表示n时刻第二传感器在x方向、y方向和z方向上的测量场，bx3(n)，by3(n)，bz3(n)分别表示n时刻第三传感器在x方向、y方向和z方向上的测量场。

n时刻的状态变量均值xn|n即为更新的状态变量。

需要说明的是，本公开实施例采用差量磁场的获取，是通过差量计算消除地磁背景，但同时信号也变为目标在传感器磁异常的差值，而并非原始观测磁异常)既保证测量过程中不受地磁场的干扰，又避免参考传感器的设置的问题。

下面通过仿真示例，阐述磁偶极子差量磁场与测量场及梯度磁场的特性。仿真磁偶极子运动轨迹如图3所示，其中黑色圆圈代表测量磁场传感器，仿真磁偶极子的磁矩定为[10，20，30]a·m²。磁偶极子在三个坐标轴投影的运动轨迹如图4a，4b，4c所示，其中的波浪动用于模拟实际运动过程中的振荡性。

两个传感器测量磁场如图5a，5b，5c所示，其中图5a代表传感器1处的测量磁场三分量，其中图5b代表传感器1处的磁梯度场中的三个典型分量，依次为x分量磁场在x方向梯度、y分量场在y方向梯度及z分量场在z方向的梯度，图5c代表传感器1，2的差量磁场。

由图5a，5b，5c可见，差量磁场与传感器原始测量磁场在磁异常幅度值上相当，而梯度磁场最小。因此，采用差量磁场进行目标跟踪时，在理论上具有与原始测量磁场相同的跟踪性能；而与采用磁梯度场跟踪相比，则具有更远的探测距离。

步骤305，将所述更新的状态变量均值及其协方差矩阵进行存储，返回步骤302进行下一时刻状态变量的更新。

该过程为迭代滤波过程，通过每一时刻的观测变量输出该时刻状态变量的估计，及其概率分布的估计(协方差矩阵)，通过这些变量为下一时刻的状态变量估计做准备，通过步骤304更新的状态变量xn|n返回步骤302后即成为n-1时刻(上一时刻)的状态变量均值xn-1/n-1。

下面通过一个具体实施例1来对采用本公开的方法进行磁偶极子跟踪的的效果进行说明：

实施例1：仿真磁偶极子跟踪实验

磁偶极子的运动轨迹如图6所示；用于实现目标跟踪的矢量磁力仪共有三个，坐标分别为(-2m，0，0)，(0，0，0)，(2m，0，0)，依次标记为传感器1，2，3。通过传感器1、2和传感器2、3分别获得差量磁场bx1、by1、bz1和bx2、by2、bz2。在原始差量场上叠加随机高斯白噪声模拟实际工作的系统噪声，噪声的标准差为100pt。利用观测磁场分量获得的差量磁场为：

zn＝[bx1(n)-bx2(n)，by1(n)-by2(n)，bz1(n)-bz2(n)，bx2(n)-bx3(n)，by2(n)-by3(n)，bz2(n)-bz3(n)]

分别采用卡尔曼滤波(extendedkalmanfilter，ekf)、无迹卡尔曼滤波(unscentedkalmanfilter，ukf)与本公开提出的蒙特卡洛卡尔曼滤波方法(montecarlokalmanfilter，mckf)，实现磁偶极子目标实时跟踪。为更好评估不同算法的跟踪性能，采用100次随机实验，将跟踪误差的统计平均值作为评判指标。不同算法的仿真实验误差结果如图7a、7b、7c所示，其中图7a为x坐标轴投影轨迹的误差，其中图7b为y坐标轴投影轨迹的误差，其中图7c为z坐标轴投影轨迹的误差。

从图7a、7b、7c可以看出，ekf与ukf具有类似的跟踪效果，mckf的初期跟踪效果较差，而后期跟踪效果明显优于ekf/ukf的跟踪结果。定性来讲，mckf在收敛速度上较ekf/ukf更慢，但稳定后在跟踪效果上跟踪精度最高。为定量分析不同算法跟踪性能，将三种跟踪方法的跟踪误差计算列举如表1(a)、表1(b)、表1(c)所示。

表1(a)x方向投影轨迹跟踪平均误差(m)

表1(b)y方向投影轨迹跟踪平均误差(m)

表1(c)z方向投影轨迹跟踪平均误差(m)

表1中列举了不同时间区间内，三个方向投影轨迹的跟踪误差平均值，其中表1(a)为x方向，表1(b)为y方向，表1(c)为z方向。从表1(a)、表1(b)可以看出mckf算法与ekf/ukf算法相比，在跟踪初期的1-40点内跟踪误差较大，随后在40-80点内mckf跟踪误差接近于ekf/ukf结果，稳定后的80-200点内，mckf的跟踪精度明显优于其余两种跟踪算法；表1(c)结果表明，在z方向投影轨迹的mckf跟踪误差与ekf/ukf算法相当。综上所述，mckf跟踪算法在响应速度上慢于ekf/ukf算法，在稳定后mckf算法在跟踪精度要优于传统的ekf/ukf跟踪算法。

综上所述，本公开的有益效果包括但不限于：

(1)本公开方法简单、实用，可有效抑制磁偶极子目标跟踪过程中地磁背景的干扰。

(2)本发明方法较传统磁梯度方法，在目标跟踪距离上更有优势。

(3)本发明中提出的蒙特卡洛卡尔曼滤波方法mckf磁偶极子跟踪方法较传统的ekf、ukf磁偶极子跟踪方法跟踪精度更高。

另外，本公开另一个实施例还提供了一种基于磁传感器阵列的磁偶极子目标跟踪系统，参见图8，所述系统800包括：确定状态变量模块801，用于建立磁偶极子模型，根据所述模型确定所述磁偶极子的状态变量；获取状态方程及观测方程模块802，用于根据所述状态变量，获取所述磁偶极子的运动状态方程以及观测方程；状态变量更新模块803，用于获取传感器阵列测量磁场的实时差量磁场，通过蒙特卡洛的方法生成随机离散样本点，将所述样本点带入所述运动状态方程与所述观测方程，获得均值与协方差估计，完成卡尔曼滤波增益的计算与状态变量的更新。

本领域技术人员可以理解，本公开的各个实施例和/或权利要求中记载的特征可以进行多种组合或/或结合，即使这样的组合或结合没有明确记载于本公开中。特别地，在不脱离本公开精神和教导的情况下，本公开的各个实施例和/或权利要求中记载的特征可以进行多种组合和/或结合。所有这些组合和/或结合均落入本公开的范围。

尽管已经参照本公开的特定示例性实施例示出并描述了本公开，但是本领域技术人员应该理解，在不背离所附权利要求及其等同物限定的本公开的精神和范围的情况下，可以对本公开进行形式和细节上的多种改变。因此，本公开的范围不应该限于上述实施例，而是应该不仅由所附权利要求来进行确定，还由所附权利要求的等同物来进行限定。