远距离分布式无源测向定位的布阵方法与流程

本发明属于目标探测技术领域，具体涉及无源测向定位在远距离定位情况下的布阵方法。

背景技术：

无源定位技术通常运用于电子侦察设备中，电子侦察设备与主动雷达相对，在探测目标时自身保持无线电静默状态，仅靠接受辐射源目标发射的无线电信号，因此其隐蔽性较好，无源定位由于缺少信号的先验信息，通常只能获得目标信号的方位角、到达时等定位信息，应用上一般以测向定位为主。无源测向定位需要电子侦察平台分别在目标的不同方向上获取多个测向信息以及自身站址，才能解算出可靠的目标地理位置，因此单站无源测向定位往往通过移动自身平台位置拉长基线长度的方式完成定位任务。而多侦察源定位构型灵活，受到各个领域的广泛关注，可以通过非集中式分布的手段，同时获取空间内多个位置对某个目标的测向信息，短时间内完成对目标的定位。现如今，目标位置的解算方法都已经比较成熟，很多方法在观测性强时都能贴近理论精度界，但其前置工作布阵的优化问题在国内鲜有讨论，根据目标的先验信息给出布阵策略非常有意义，同样能大大提高辐射源目标的定位精度。

技术实现要素：

本发明针对多侦察源分布式无源测向定位，在远距离侦察情况下对具有先验信息目标，提出了观测站位置该如何分布的布阵策略。本发明首先建立所提问题的场景模型，解释分布式多侦察源中的远距离侦察情况的定义，然后通过理论推导得出定位效果最优的布阵策略，最后再通过仿真验证布阵策略的正确性。

本发明所采用的技术方案为：

首先对问题场景建立模型，不妨设辐射源目标所处的位置为坐标系原点x＝(0,0)^t建立坐标系，假定无源定位系统有n个电子侦察源，每个电子侦察源的位置为ui＝(xi,yi)^t，ri为电子侦察源到目标的距离；假定电子侦察编队的中心为其重心不妨将目标指向电子侦察编队中心的方向作为x轴负方向，即u＝(-r,0)^t，r为目标和电子侦察编队中心的距离；我们再假定电子侦察编队的基线长度为r，基线长度定义为电子侦察源距离中心的最远距离，即本发明中对于远距离侦察的定义为电子侦察编队的基线长度r不超过目标与电子侦察编队中心距离r的十分之一，即r<0.1r，定位模型如图1所示。

假设第i个电子侦察源接收到的辐射源目标到达方位角为θi，则观测向量可以表示为θ＝[θ1,θ2,…,θn]^t，观测方程为：

假设每个电子侦察源的方位角测量误差相互独立且服从同一高斯分布：

e(ni)＝0

e(ninj)＝σ²δ(i-j)(2)

σ＝π/180

设n阶单位矩阵表示为in×n，则测量噪声n＝[n1,n2,…,nn]的协方差矩阵为：

q＝σ²in×n(3)

根据观测方程，我们可以得到观测方程的雅克比矩阵f为：

观测向量θ的费谢尔信息矩阵为：

费谢尔信息矩阵行列式的值如下所示：

上文提到，远距离侦察的约束条件为r<0.1r，ri的取值范围为[0.9r,1.1r]，并不是函数值的主要影响变量；又由于θi的值较小，根据洛必达法则有可以得到新的评价函数公式7：

代价函数的第一项中的与各电子侦察站的接收信号方位角的方差有直接关联；在远距离定位任务的约束条件下，第二项的值较小对代价函数的值影响较小；第三项在布阵对称分布时值达到最小为0。因此我们可以得到以下布阵准则与方法：

a.假定电子侦察平台两两之间距离不大于kkm，不小于kkm；实际中最大基线限制kkm和最小距离限制kkm根据需求设定；

b.将侦察平台尽可能等分置于角度最大的两端，令其方差达到最大；

一方面，针对具有一定先验信息的目标或对特定区域目标的定位任务，本专利的方差最大布阵准则可以作为观测站位置如何分布的依据；另一方面，可以根据多个观测站所接收到的方位角数据，依据方差最大准则可以快速的判断本次定位结果的可靠性。

附图说明

图1为远距离侦察定位模型示意图；

图2为远距离侦察布阵策略示意图；

图3为仿真条件的侦察布阵示意图；

图4为侦察平台个数为2个时定位性能与阵形拓扑结构的关系图；

图5为侦察平台个数为3个时定位性能与阵形拓扑结构的关系图；

图6为侦察平台个数为4个时定位性能与阵形拓扑结构的关系图；

仿真结果

通过仿真侦察平台分别为2～4个时，侦察平台位置不同时，定位性能的比较图；仿真中布阵相对位置如图4所示，其中定位性能用crlb界限表示：

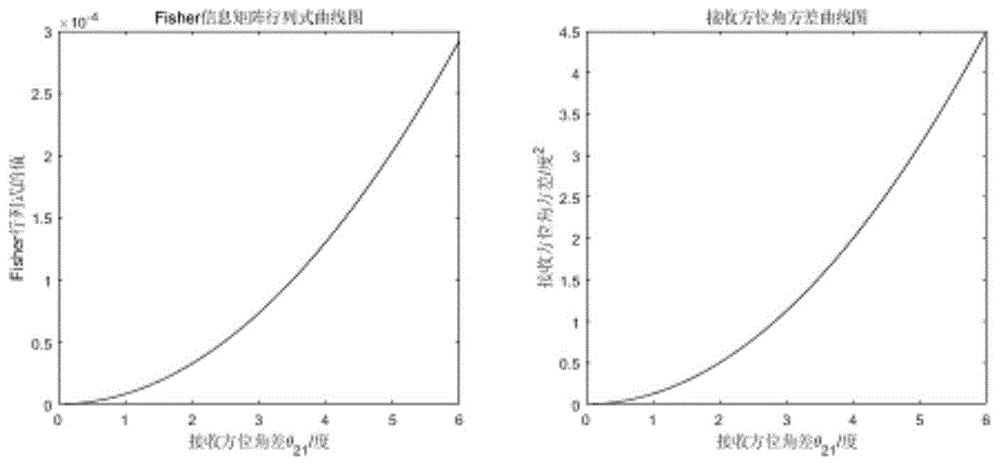
当仿真侦察平台个数为2个时，假设其中一个侦察平台位于布阵区域的最左侧并假设其接收到目标信号的方位角为0°，两侦察平台接收方位角差θ21最大不超过6°，其定位性能与其接收方位角差的关系图如图4所示：

当仿真侦察平台个数为3个时，假设其中一个侦察平台位于布阵区域的最左侧并假设其接收到目标信号的方位角为0°，其余侦察平台与其接收方位角差θ21,θ31最大不超过6°，其定位性能与其接收方位角差的关系图如图5所示：

当仿真侦察平台个数为4个时，假设其中两个侦察平台分别位于布阵区域的最左侧与最右侧，其接收到目标信号的方位角分别为0°和θ41＝6°，其余侦察平台在两侦察平台之间θ21,θ31<6°，其定位性能与其接收方位角差的关系图如图6所示：

可以从图4，5和6中看出，当侦察平台的布阵按本专利提出的准则分布时，最为定位性能目标函数的fisher信息矩阵行列式的值最大，定位性能最优，证明了本专利布阵准则的正确性；同时我们可以看到，定位性能与各侦察平台的接收方位角的方差呈正相关，各侦察平台的接收方位角的方差越大，则定位性能越好，从理论上验证了布阵准则的正确性。