一种基于机器人盘式打磨的工件表面粗糙度预测方法与流程

本发明属于工业机器人自动化技术加工领域，具体涉及一种基于机器人盘式打磨的工件表面粗糙度预测方法。

背景技术：

以工业机器人为执行手段的磨抛加工是提升复杂曲面零件加工表面质量和精度的重要工艺。盘式打磨头和辊式打磨头是机器人打磨加工中的两种常用末端执行器。对于如高铁白车身、新能源客车车体等较平整面的打磨，相比于后者，盘式打磨有着更高的效率，且能获得更好的表面平整度。但由于打磨盘上一点处的圆周线速度与其到打磨盘圆心的距离成正比，因此会导致加工面上沿着径向分布的不同位置的打磨速度不同，进而导致加工表面粗糙度不均匀的问题。如果采用以被打磨点线速度为特征值的粗糙度预测模型将无法实现该加工表面粗糙度的准确预测。因此研究机器人盘式打磨工件表面粗糙度分布规律，提出一种基于机器人盘式打磨的工件表面粗糙度预测方法对提高打磨质量有着重要的意义。

技术实现要素：

本发明的目的就是针对盘式打磨的特点而提供一种基于机器人盘式打磨的工件表面粗糙度预测方法。

本发明的目的可以通过以下的技术方案实现：

一种基于机器人盘式打磨的工件表面粗糙度预测方法，其特征在于：包括如下步骤：

步骤s1、选取影响盘式打磨粗糙度的工艺参数建立机器人盘式打磨工件表面粗糙度的预测模型；

步骤s2、设计正交试验获取样本数据；

步骤s3、根据多元线性回归确定预测模型参数数值；

步骤s4、利用所得参数进行预测。

作为优选，在步骤s1中，选取打磨压强p、机器人进给速度vt、打磨盘转速n、被打磨工件上一点到打磨轨迹中线的距离d这四个影响盘式打磨粗糙度的工艺参数作为预测模型中的特征值。

作为优选，在步骤s1中，建立预测模型具体方法如下：

在一次打磨后，工件表面粗糙度ra会在ra0～rae之间，其中ra0为工件初始表面粗糙度，rae为所用打磨工具能得到的工件表面粗糙度极限值，因此，可以将表面粗糙度ra的预测模型表示为：

其中，rap为表面粗糙度预测值，m为参数p、vt、n、d的多元函数，且令m＞0，故的值域为(0,1)，选用指数函数作为拟合函数，可得：

其中，a、θ1、θ2、θ3和θ4为系数，且a为正数；

公式(2)可化为：

对公式(3)的等式两边取自然对数，可得

令θ0＝ln(a)，x0＝1，x1＝p，x2＝vt，x3＝n，x4＝d，则可得线性回归方程的预测模型：

其中，x1,x2,x3,x4表示影响该预测模型的四个特征，θ0,θ1,θ2,θ3,θ4为该预测模型的参数，即四个特征的系数，x0为常数，i表示序数。

作为优选，所述步骤s2中正交试验设计具体包含以下步骤：

步骤s2.1、针对打磨压强p、机器人进给速度vt、打磨盘转速n、被打磨工件上一点到打磨轨迹中线的距离d四个因素，每个因素设计三个水平，按照正交表l9(3⁴)设计试验；

步骤s2.2、控制机器人夹持打磨盘在工件上停驻打磨20s以上，测量打磨后工件表面粗糙度值，即为所用打磨工具能得到的工件表面粗糙度极限值rae；

步骤s2.3、在打磨前测量并记录工件原始表面粗糙度ra0，按照正交试验表进行试验，通过离线编程，控制机器人夹持打磨头沿直线轨迹移动一段足够距离，要保证打磨过程中整个打磨盘完全打磨经过被测量点，测量打磨后表面粗糙度ra，并根据计算样本真实值y；

作为优选，所述步骤s2.2中、测量所用打磨工具能得到的工件表面粗糙度极限值rae时，控制机器人夹持打磨盘在工件上停驻打磨时间为25-50s。

作为优选，步骤s3中，在线性回归中，线性回归假设特征和结果满足线性关系，特征对结果的影响可以通过特征前的系数体现，用矩阵形式表示公式(5)预测模型，得

yp＝θ^tx公式(6)

其中，x是预测模型的特征值向量，包括x0,x1,x2,x3,x4，θ是预测模型的偏置项，包括θ0,θ1,θ2,θ3,θ4；

样本真实值y和估计值yp存在误差，用损失函数对预测模型做出评估，损失函数可表示为：

其中，yp是预测值向量，包含每组试验数据的预测值，是第j组实验数据的预测值；y是实际值向量，包含每组实验数据的实际值，y^(j)是第j组实验数据的实际值，n为实验数据的总组数；

使用最小二乘法，求解损失函数的最小值，得到因子的最优参数，θ0,θ1,θ2,θ3,θ4，并由θ0＝ln(a)计算出系数a。

作为优选，使用最小二乘法，求解损失函数的最小值时可通过标准方程求解使损失函数最小的θ值，标准方程表示如下：

θ＝(x^t·x)^-1·x^t·y公式(8)

求解代公式(8)标准方程，得到模型的最优参数，θ0,θ1,θ2,θ3,θ4，并由θ0＝ln(a)计算出系数a。

作为优选，在步骤s3中，可以采用matlab的regress命令完成线性回归的计算。

作为优选，步骤s4中，将步骤s3中所求得的最优参数θ1,θ2,θ3,θ4以及由方程θ0＝ln(a)求解出的a的值代入预测模型，对机器人盘式打磨工件表面粗糙度进行预测。

本发明产生的有益效果是：

本发明提供了一种预测机器人盘式打磨工件表面一点处表面粗糙度的方法，可用于研究盘式打磨工件表面粗糙度分布的规律，而据此调整打磨工艺参数或改进机器人的加工轨迹规划以提高加工质量。

附图说明

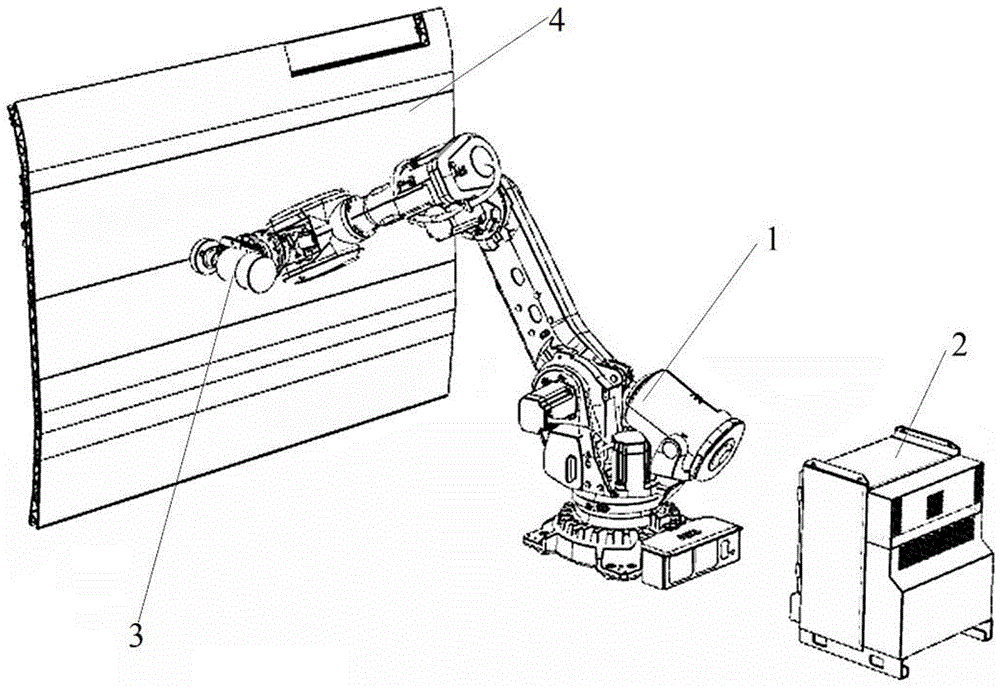
图1为本发明实施例中机器人盘式打磨系统简图；

图2为本发明实施例中打磨表面粗糙度预测原理图；

图3为本发明实施例中盘式打磨简化示意图；

图4为本发明实施例中图3中工件上a-g点打磨过程中圆周线速度vt随时间t变化图像；

图5为本发明实施例中l9(3⁴)正交试验表范例。

1-工业机器人，2-机器人控制柜，3-机器人盘式打磨头，4-被打磨工件。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。

如图1所示，为本发明实施例中机器人盘式打磨系统示意图，其包括工业机器人，机器人控制柜，机器人盘式打磨头以及被打磨工件，机器人控制柜控制工业机器人带动机器人盘式打磨头按照设定程序在被打磨工件表面行走打磨，该硬件系统采用现有技术中常规的机器人即可。

如图2所示，一种基于机器人盘式打磨的工件表面粗糙度预测方法，包括以下步骤：

s1、盘式打磨表面粗糙度预测模型的建立

盘式打磨常用于对平面的打磨。基于现有研究与经验，机器人平面磨抛中影响表面粗糙度的主要工艺参数有：打磨正压力fa；打磨工具圆周速度v0；机器人进给速度vt。但在盘式打磨中，特殊的是，工件上一点的打磨工具圆周速度随着机器人沿轨迹的运动是不断变化的。

取被打磨工件上垂直于打磨轨迹的一条线段为参考线，如图3，a-g点为参考线上等距分布的7个点，a点位于打磨轨迹的中线上，g点位于打磨轨迹的边缘。从打磨盘运动至与该线段相切开始，线段上一点的工具圆周速度v0可以表示为打磨盘转速n(r/min)，机器人进给速度v0(mm/s)，以及被打磨工件上一点到打磨轨迹中线的距离d(mm)的函数，如下式：

其中，r为打磨盘的半径，单位为mm；t为时间，单位为s；t0为自打磨盘与线段相切到线段上该点被打磨所经过的时间，单位为s。

图3中工件上a-g点打磨过程中圆周线速度v随时间t变化图像如图4，其中打磨盘半径r取100mm，转速n取1500r/min，机器人进给速度vt取10mm/s。

此外，取决于打磨盘的半径r，在相同打磨正压力的情况下，作用在工件上的打磨压强也并不相同，进而也会对打磨表面粗糙度产生影响。

因此，在盘式打磨中实际影响打磨表面粗糙度的因素为打磨压强p；机器人进给速度vt；打磨盘转速n；被打磨工件上一点到打磨轨迹中线的距离d。

在一次打磨后，工件表面粗糙度ra会在ra0～rae之间，其中ra0为工件初始表面粗糙度，rae为所用打磨工具能得到的工件表面粗糙度极限值。因此，可以将表面粗糙度ra的预测模型表示为：

其中，rap为表面粗糙度预测值，m为参数p、vt、n、d的多元函数，且令m＞0，故的值域为(0,1)，选用指数函数作为拟合函数，可得：

其中，a、θ1、θ2、θ3和θ4为系数，且a为正数。

公式(2)可化为

对公式(4)等式两边取自然对数，可得

令θ0＝ln(a)，x0＝1，x1＝p，x2＝vt，x3＝n，x4＝d，则可得线性回归方程的预测模型：

其中，x1,x2,x3,x4表示影响该预测模型的四个特征，θ0,θ1,θ2,θ3,θ4为该预测模型的参数，即四个特征的系数，x0为常数，i表示序数。

s2、样本数据的获取

s2.1设计正交试验

要得到更准确的粗糙度预测模型，需要有足够的，具有代表性的输入数据。设计正交试验可以高效、快速的获取所需的样本数据。在s1的模型中，有打磨压强p，机器人进给速度vt，打磨盘转速n，被打磨工件上一点到打磨轨迹中线的距离d四个因素，每个因素设计三个水平，按照正交表l9(3⁴)设计试验。

s2.2表面粗糙度极限值rae的测量

研究结果表明，当使用某种打磨工具进行打磨时，随着打磨时间的增加，工件表面粗糙度将不断减小并趋于某一固定值，该固定值即为所用打磨工具所能得到的工件表面粗糙度极限值rae。一般控制机器人夹持打磨盘在工件上停驻打磨20s以上即可，本实施例基于提供最优实施例为停驻打磨30s，测量打磨后工件表面粗糙度值，即为rae。

s2.3试验过程

在打磨前测量并记录工件原始表面粗糙度ra0，按照正交试验表进行试验，通过离线编程，控制机器人夹持打磨头沿直线轨迹移动一段足够距离，要保证打磨过程中整个打磨盘完全打磨经过被测量点，测量打磨后表面粗糙度ra，并根据计算样本真实值y。

s3、根据多元线性回归确定预测模型参数数值

线性回归假设特征和结果满足线性关系，特征对结果的影响可以通过特征前的系数体现。用矩阵形式表示公式(6)预测模型，得

yp＝θ^tx公式(7)

其中，x是预测模型的特征值向量，包括x0,x1,x2,x3,x4，θ是预测模型的偏置项，包括θ0,θ1,θ2,θ3,θ4；

样本真实值y和估计值yp存在误差，用损失函数对预测模型做出评估，损失函数可表示为：

其中，yp是预测值向量，包含每组试验数据的预测值，是第j组实验数据的预测值；y是实际值向量，包含每组实验数据的实际值，y^(j)是第j组实验数据的实际值，n为实验数据的总组数；

使用最小二乘法，求解损失函数的最小值，得到因子的最优参数，具体的，可通过标准方程求解使损失函数最小的θ值，标准方程表示如下：

θ＝(x^t·x)^-1·x^t·y公式(9)

求解代公式(8)标准方程，得到模型的最优参数，θ0,θ1,θ2,θ3,θ4，并由θ0＝ln(a)计算出系数a。

由于特征数量并不大，使用matlab的regress命令，可以简便地完成线性回归的相关计算。regress命令常用于一元或多元线性回归，其本质是最小二乘法。对试验所得数据进行预处理，根据得到各组数据所对应的y值。通过程序计算，可以得到回归方程的各系数θ0、θ1、θ2、θ3和θ4的值，并可由θ0＝ln(a)计算出系数a。除此之外，使用regress命令还可以得到回归系数的区间估计、残差、置信区间等，可以用于判断拟合模型的准确性。

s4、利用所得参数进行预测

将步骤s3中所求得的最优参数θ1、θ2、θ3和θ4以及由方程θ0＝ln(a)求解出的a的值代入预测模型中，对机器人盘式打磨工件表面粗糙度进行预测。

以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，可以根据上述说明加以简单的变换实现相同的技术效果。凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。