一种基于PP波反射系数能谱的薄层厚度预测方法与流程

本发明涉及地震技术反演方法研究领域，具体涉及一种基于pp波反射系数能谱的薄层厚度预测方法。

背景技术：

薄层与薄互层在我国是广泛存在的，随着我国化石能源勘探的发展，薄砂岩和薄煤层的识别越来越受到重视，薄层的研究已经成为岩性油气藏研究的重要部分。研究表明，薄层厚度定量预测是薄层物性、地震属性反演分析的基础，了解厚度变化对工业储量评价和开采极为重要。

相比于厚层，薄层在地震勘探中更加难以解译，其顶底界面在地震记录上很难分辨，薄层厚度预测也成为一个难题。针对这一问题，前人已经做了许多探索。薄层厚度预测研究从时间域^[2-5]到频率域^[6-15]，从特殊模型到一般模型，在探索中进步和完善。时间域方法根据振幅和厚度的关系来定量预测厚度，频率域中可以选择峰值频率和陷频周期以及振幅谱这些属性来计算厚度。显然，前人为薄层厚度预测提供了指导性结论，然而现有的技术，由于方法理论不完善的限制，对于薄层厚度的反演并没有达到工业生产的要求，这在一定程度上制约了工业领域对于薄层的认知，薄层厚度预测的精度仍需要提高^[16]。所以，研究和发展新的薄层定量预测技术对化石能源勘探开发具有重要的现实意义。

参考文献

[1]yangc,wangy,luj.weakimpedancedifferenceapproximationsofthin-bedpp-wavereflectionresponses[j].journalofgeophysics&engineering,2017,14(4).

[2]widessmb.howthinisathinbed？[j].geophysics,1973,38(6):1176-1180.

[3]kallweit,r.s,andwood,l.c,thelimitsofresolutionofzero-phasewavelets:geophyiscs,,1982,47,1035-1046.

[4]chung,h.m.,andd.c.lawton,amplituderesponsesofthinbeds:sinusoidal

approximationversusrickerapproximation:geophysics,1995,60,223–230

[5]刘震,张万选,张厚福.储层厚度定量解释方法研究[j].石油地球物理勘探,1991,26(6):777-784.

[6]窦易升.薄层厚度定量解释的振幅谱平方比法[j].石油地球物理勘探,1995,v30(s2):57-65.

[7]partyka,g.a.,gridley,j.a.,andlopez,j.a.,interpretationalaspectsofspectraldecompositioninreservoircharacterization:theleadingedge,1999,18,353–360.

[8]partyka,g.a.,2005,spectraldecomposition:segdistinguishedlecture.

[9]marfurt,k.j,kirlin,etal.narrow-bandspectralanalysisandthin-bedtuning[j].geophysics,2001,66(4):1274-1283.

[10]puryearci.layer-thicknessdeterminationandstratigraphicinterpretationusingspectralinversion:theoryandapplication[j].geophysics,2008,73(73):r37.

[11]李雪英,李东庆,白诗缘.薄层研究方法综述[j].地球物理学进展,2014,29(5):21-97-2203.

[12]周开明.薄层的二阶功率谱特征研究及厚度预测[j].石油物探,2008,47(1):30-34.

[13]sunluping,zhengxiaodong,etal.thin-bedthicknesscalculationformulaanditsapproximationusingpeakfrequency[j].appliedgeophysics,2009,6(3):234-240.

[14]yangd,pengg,chenz,etal.thinbedthicknesscalculationfromspectralcorrelation[c].segtechnicalprogramexpanded.2017,2305-2309.

[15]高君,曹思远,吕雪雁,等.峰值频率法估算薄层厚度[j].地球物理学进展,2018(1).

[16]王赟,杨春,芦俊.薄互层弹性波反演面临的困境[j].地球物理学报,2018.

技术实现要素：

针对现有技术的不足，本发明旨在提供一种基于pp波反射系数能谱的薄层厚度预测方法，对于随频率变化的薄层反射系数，考虑其能谱，在频率域进行厚度预测，公式简单，计算快捷，能够高精度的进行薄层厚度预测。

基于上述技术目的，本发明采用如下技术方案：

一种基于pp波反射系数能谱的薄层厚度预测方法，包括如下步骤：

s1、获取薄层反射系数能谱；

s2、利用所述薄层反射能谱求取对频率的一阶及三阶导数：

(r²(f))′＝-4a1a2πδtsin(2πfδt)(1)；

(r²(f))″′＝16a1a2π³(δt)³sin(2πfδt)(2)；

其中，

a1＝r1

vpa1＝(vp2+vp1)/2；δvp1＝vp2-vp1；

ρa1＝(ρ2+ρ1)/2；δρ1＝ρ2-ρ1；

vpa2＝(vp3+vp2)/2；δvp2＝vp3-vp2；

ρa2＝(ρ3+ρ2)/2；δρ2＝ρ3-ρ2；(6)；

r1、r2分别是顶界面和底界面的pp波反射系数，δt为薄层的时间厚度，vpi、ρi(i＝1,2,3)分别为薄层模型各层i的纵波速度和密度，f为频率；

s3、利用步骤s2中求取的对频率的一阶及三阶导数获取薄层时间厚度如下：

s4、将步骤s3得到的薄层时间厚度计算公式转换到深度域得到薄层厚度如下：

进一步地，步骤s1中，对实际地震数据进行反褶积运算得到薄层复反射系数，并利用薄层复反射系数便可得到薄层反射系数能谱。

本发明的有益效果在于：本发明方法利用了薄层反射系数能谱随频率变化的特征，在频率域进行公式推导，以更少的近似来进行薄层厚度预测。本发明方法中对于随频率变化的薄层反射系数，考虑其能谱，在频率域进行厚度预测，公式简单，计算快捷，能够高精度的进行薄层厚度预测。

附图说明

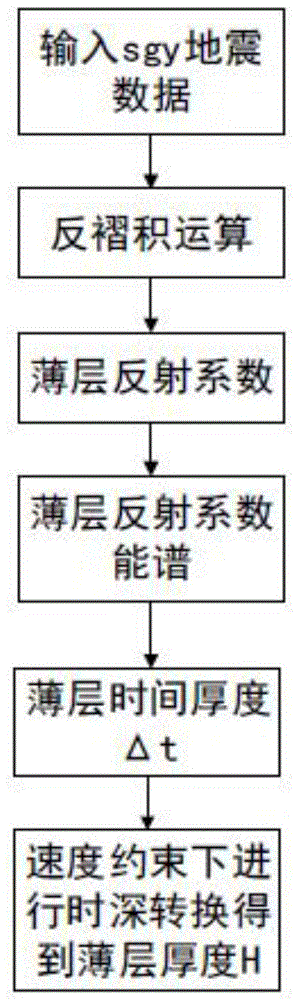
图1为本发明实施例2方法流程图；

图2为本发明实施例2理论模型反褶积流程；

图3为本发明实施例2实际模型反褶积流程；

图4为本发明实施例3设计的楔状模型；

图5为本发明实施例3采用的楔状模型合成记录图；

图6为本发明实施例3中楔状模型厚度求解对比图；

图7为本发明实施例4的实际数据目标层示意图；

图8为本发明实施例4的实际模型反射系数能谱及厚度反演结果示意图。

具体实施方式

以下将结合附图对本发明作进一步的描述，需要说明的是，本实施例以本技术方案为前提，给出了详细的实施方式和具体的操作过程，但本发明的保护范围并不限于本实施例。

实施例1

一种基于pp波反射系数能谱的薄层厚度预测方法，包括如下步骤：

s1、获取薄层反射系数能谱；

s2、利用所述薄层反射能谱求取对频率的一阶及三阶导数：

(r²(f))′＝-4a1a2πδtsin(2πfδt)(1)；

(r²(f))″′＝16a1a2π³(δt)³sin(2πfδt)(2)；

其中，

a1＝r1

vpa1＝(vp2+vp1)/2；δvp1＝vp2-vp1；

ρa1＝(ρ2+ρ1)/2；δρ1＝ρ2-ρ1；

vpa2＝(vp3+vp2)/2；δvp2＝vp3-vp2；

ρa2＝(ρ3+ρ2)/2；δρ2＝ρ3-ρ2；(6)；

r1、r2分别是顶界面和底界面的pp波反射系数，δt为薄层的时间厚度，vpi、ρi(i＝1,2,3)分别为薄层模型各层i的纵波速度和密度，f为频率；

式(1)是基于薄层模型和弱阻抗差近似公式^[1]获得的垂直入射假设下的薄层复反射系数公式，则是其薄层反射能谱形式。

s3、利用步骤s2中求取的对频率的一阶及三阶导数获取薄层时间厚度如下：

s4、将步骤s3得到的薄层时间厚度计算公式转换到深度域得到薄层厚度如下：

通过上述方法，可以实现针对弱阻抗差薄层，在垂直入射情况下进行厚度预测。

实施例2

图1为本实施例2的流程图，输入数据为.sgy地震数据，进行反褶积运算得到薄层复反射系数，将薄层复反射系数进行运算便可得到薄层的反射系数能谱，接下来利用式(1)(2)(7)(8)进行厚度预测得到薄层的时间厚度以及实际层厚。

其中反褶积运算的实现过程分为理论模型反褶积运算(图2)和实际数据模型反褶积运算(图3)。下面就两种运算进行介绍。

理论模型反褶积运算：如图2所示，理论模型反褶积运算是输入地震数据s(t)和雷克子波w(t)，利用fft(快速傅立叶变换)变换到频率域得到s(f)和w(f)，基于频率域地震记录是子波和反射系数的乘积理论，可以得到，反射系数是地震记录除以子波，这样便可得到薄层的反射系数，继而得到反射系数能谱，在此基础上就可以利用式(1)(2)(7)(8)进行厚度预测。

实际数据模型反褶积运算：如图3所示，在商业软件hrs中将复数道进行分频处理得到多个单频数据，将单频目标层地震角道集数据输入，用hilbert变换构造复地震道，求取每个实部地震道和虚部地震道的最大振幅，分别为sr(i)和si(i)(i表示第i个地震道，i<＝总道数)，sr(1)和si(1)分别表示第一道地震记录实虚部，是垂直入射道集，或者是近似垂直角道集。对实际数据来说，确定精准子波是很困难的，本实施例中是薄层反射系数能谱(振幅)进行计算，假设单频假设下，子波的最大振幅是不变的，用如下方法进行子波近似计算：

利用测井模型计算垂直入射反射系数，实虚部分别为rr和ri，此时利用基于频率域地震记录是子波和反射系数的乘积理论，可以得到薄层的反射系数，wr和wi。反射系数是地震记录除以子波，只考虑振幅，分别计算实部和虚部反射系数振幅，组合成复数这样便可得到薄层的反射系数，取垂直入射角道集计算的反射系数，得到反射系数能谱，在此基础上就可以利用式(1)(2)(7)(8)进行厚度预测。

实施例3

理论模型计算：

为不失一般性，设计四种楔状体模型(如图4所示)，设震源子波为ricker子波，主频50hz，合成地震记录如图5所示，其中(a)、(b)、(c)、(d)分别为模型1、模型2、模型3、模型4的合成地震记录。利用实施例1所述方法预测厚度并将预测结果与widess方法、chung&lawton基于ricker零相位子波假设表达式、sun提出的基于峰值频率的薄层厚度预测方法(pf方法)进行对比分析。widess方法只适用于第四种模型(顶底界面反射系数极性相反大小相同的模型，即图(d))，加入widess方法是为了对图(d)所示模型进行更为全面的分析对比。

利用widess方法^[2]：

ad是地震记录振幅，am是震源子波的波峰波谷振幅平均值，r是顶底界面相对反射系数，λ是薄层的主波长，h是薄层厚度。

利用chung&lawton基于ricker零相位子波假设表达式^[4]：

公式中armax表示雷克近似下的地震反射波振幅，ai表示地震子波的振幅，h表示薄层厚度，λ表示主频对应的主波长，r1,r2分别表示顶底界面的反射系数振幅。

上述两种方法是在时间域进行厚度预测，求解厚度只需从上述公式中求出厚度即可。

sun提出的基于峰值频率的薄层厚度预测方法^[13]是在频率域进行求解，具体公式如下：

根据不同近似程度以及适用模型的不同，sun将其分为三类：

其中r＝r1/r2,fp-s,fp分别是地震记录的峰值频率和ricker子波的峰值频率，τ表示的是薄层的双程旅行时，下标1、2、3表示公式近似阶数。对于顶底反射系数极性相同的薄层，一阶和二阶近似公式均适用，二阶近似公式具有更高的精度；对于顶底反射系数极性相反的薄层，一阶近似公式不适用，二阶近似公式仅当薄层厚度较小时适用。对于等幅反极性型薄层，一阶和二阶近似公式均不适用，需使用三阶近似公式，所以公式是针对于r＝-1假设的。

利用上述理论进行模型测试及对比分析：

表1

(注：表1中速度的单位为：m/s，密度的单位为：g/cm3。r1、r2为顶底界面反射系数)

四个楔状模型的参数如表1所示，通过薄层精准反射系数逐道计算出薄层模型的反射系数，在此基础上，将数据计算成为薄层反射系数能谱，用差分方法进行求导并计算出薄层的厚度，结果如图6所示，其中图6(a)、(b)、(c)(d)分别是利用实施例1方法和其他三种方法对模型1、2、3、4的薄层厚度求解对比示意图。

从图6可以看出，与其他几种方法对比，利用实施例1方法得到的预测曲线最接近真实厚度曲线(误差小于5％)，预测结果要好于其它三种方法，且实施例1所述方法计算过程中不需要考虑反射系数的大小，并且在后续计算中还可以估计反射系数大小。结果表明实施例1所述方法改善了薄层预测的精度，能精准的预测薄层厚度。

实施例4

以下为鄂尔多斯杭锦旗地区j86井约束下的实例(图7)。

表2实际数据测井模型

(注：表2中速度的单位为：m/s，密度的单位为：g/cm3。r1、r2为顶底界面反射系数)

图8(a)为实际模型反射系数能谱，图8(b)为厚度反演结果。通过前期处理得到薄层反射系数能谱，用差分方法进行求导并计算出薄层的厚度，如图8(b)所示。实际模型的真实层厚为5.5m，反演的薄层厚度为5.75m，误差只有4％，属于工业界可接受范围(工业界一般要求误差不大于10％)。结果表明，实施例1所述方法在有井约束情况下能高精度的对实际薄层介质进行厚度预测。

对于本领域的技术人员来说，可以根据以上的技术方案和构思，给出各种相应的改变和变形，而所有的这些改变和变形，都应该包括在本发明权利要求的保护范围之内。