一种基于LSTM和多传感器融合的室内定位方法与流程

本发明涉及室内定位技术领域，特别是涉及一种基于lstm和多传感器融合的室内定位方法。

背景技术：

室内定位系统(indoorpositioningsystem，ips)是指在建筑物中使用移动设备收集无线电波、磁场、声波信号或其他的传感信息来定位物体或人的系统。室内定位是移动互联网时代的基础服务，能够给消费者提供更加优质的服务，为企业带来经济效益。随着室内定位技术的不断发展，室内定位技术将在人们的日生活领域、智能景区等行业应用领域以及地铁等地下公共领域发挥重要作用。虽然目前室内定位技术百花齐放，比如基于无限信号的红外和超声波定位技术、基于粒子滤波和地磁的定位技术、基于wifi的定位技术和基于计算机视觉和图像的定位技术等。然而，这些定位技术的精度在3米左右，虽然能满足当下的定位需求，但是大多都需要部署额外设备，例如每隔6-8m布设一个ibeacon，成本很高。因此，迫切需要一种低成本、易部署和高精度的室内定位方法。

技术实现要素：

针对现有技术存在的问题，本发明提供一种基于lstm和多传感器融合的室内定位方法，能够提高室内定位的精度，且成本低、容易部署。

本发明的技术方案为：

一种基于lstm和多传感器融合的室内定位方法，其特征在于，包括下述步骤：

步骤1：使待定位的行人配置手机，通过手机的加速度计、地磁传感器、陀螺仪，以采样频率f分别采集行人在第t时刻的三轴加速度at＝[axt,ayt,azt]^t、三轴磁力值mt＝[mxt,myt,mzt]^t、三轴角速度ωt＝[wxt,wyt,wzt]^t，采集行人在第t时刻的位置坐标(posxt,posyt)，形成数据集，并将数据集传输给计算机，利用计算机对数据集进行预处理；其中，t∈{1,2,...,n}，n为一个行走周期中采集的样本总数；

步骤2：利用wifi信息对行人进行粗定位：

步骤2.1：在离线阶段，建立行人位置和指纹之间的对应关系：按室内结构对每个楼层进行划分，对所有房间和走廊进行编号并将每个房间作为一个网格、将走廊划分成多个网格，在每个网格中随机选取多个采样点；利用wifi传感器采集在每个采样点上手机能连接到的ap的rss构成位置指纹，并记录ap的id及该采样点对应的房间编号或走廊编号，构建wifi指纹库；

步骤2.2：在在线阶段，在wifi指纹库中利用欧氏距离找到与当前行人手机接收到的ap的rss最近的指纹，并利用三角定位法，计算出行人的初始位置(x0,y0)；

步骤3：利用三轴加速度数据对行人进行计步并进行步长估计，利用三轴磁力值数据和三轴角速度数据对行人进行方向估计，形成行人运动模型，并结合wifi粗定位获得的初始位置，对行人位置进行估算：

步骤3.1：采用滑动窗口方式，利用当前时间窗口内的三轴加速度数据对行人进行计步：计算第t时刻的步行参数为

若vat＝1，则第t时刻行人走了一步；若vat＝0，则第t时刻行人未走一步；其中，accelow、accehigh分别为加速度峰值的下限、上限，δt为两个相邻步的时间间隔，tlow、thigh分别为两个相邻步的时间间隔的下限、上限；

步骤3.2：对行人进行动态步长估计：计算行人的步长为

lt＝αh+βw+γf

其中，h为行人的身高，w为行人的体重，f为步频，f＝f/n，α、β、γ均为参数；

步骤3.3：利用三轴磁力值数据和三轴角速度数据对行人进行方向估计：

步骤3.3.1：计算手机的俯仰角θt、横滚角偏航角ψt对应的旋转矩阵分别为

步骤3.3.2：计算手机坐标系到地球坐标系的坐标转换矩阵为

步骤3.3.3：利用三轴角速度数据计算手机的偏航角为ψt1；

步骤3.3.4：利用三轴加速度数据计算手机的俯仰角θt、横滚角分别为

其中，g为重力加速度；

步骤3.3.5：利用三轴磁力值数据计算手机的偏航角ψt2为

步骤3.3.6：将利用三轴角速度数据计算的偏航角ψt1作为状态向量、将利用三轴磁力值数据计算的偏航角ψt2作为观测向量，进行卡尔曼滤波，得到修正后的偏航角ψt；

步骤3.4：估算第t时刻行人的位置为(xt,yt)；

其中，xt＝xt-1+ltsinψt，yt＝yt-1+ltcosψt；

步骤4：构建并训练行人定位的lstm模型，利用训练后的lstm模型对行人位置进行预测：

步骤4.1：用行人在第t时刻的三轴磁力值的模值mt及位置坐标(posxt,posyt)构建训练数据集in＝{in1,in2,...,int,...,inn}；

其中，int＝(mt,pt)，pt＝(posxt,posyt)；

步骤4.2：设定lstm模型的输出的激活函数为tanh函数、三个门的激活函数均为sigmoid函数σ；

步骤4.3：利用训练数据集，对lstm模型进行训练：

步骤4.3.1：计算遗忘门的输出为

ft＝σ(wf[ht-1,int]+bf)

其中，ht-1为上一时刻lstm模型的输出，wf为遗忘门的权重，wf由ht-1的权重和int的权重构成，bf为遗忘门的偏置；

步骤4.3.2：计算输入门的输出为

it＝σ(wi[ht-1,int]+bi)

利用tanh激活函数建立新的候选向量为

更新记忆单元为

其中，wi为输入门的权重，bi为输入门的偏置；

步骤4.3.3：计算输出门的输出为

ot＝σ(wo[ht-1,int]+bo)

利用tanh激活函数控制记忆单元，得到lstm模型在第t时刻的输出为

其中，wo为输出门的权重，bo为输出门的偏置；

步骤4.4：沿时间方向的反向传播过程，对lstm模型进行训练：

步骤4.4.1：定义目标函数为

定义第t时刻lstm模型的误差项为

其中，为行人位置的预测坐标；

步骤4.4.2：计算遗忘门、输入门、输出门、候选向量的加权输入分别为

netf,t＝wf[ht-1,int]+bf＝wfhht-1+wfinint+bf

neti,t＝wi[ht-1,int]+bi＝wihht-1+wiinint+bi

neto,t＝wo[ht-1,int]+bo＝wohht-1+woinint+bo

得到遗忘门、输入门、输出门、候选向量加权输入的误差项分别为

计算第t-1时刻lstm模型的误差项为

利用全导数公式可得

计算lstm模型沿时间方向反向传播到第k时刻的误差项为

步骤4.4.3：将误差项向上一层传播，假设当前为第l层，定义第l-1层的误差项是目标函数对第l-1层加权输入的导数

计算第l层的输入为

其中，f^l-1为第l-1层的激活函数；

利用全导数公式将误差传递到上一层为

计算第t时刻遗忘门的梯度为

将各时刻梯度加一起，得到第t时刻遗忘门权重的梯度为

步骤4.5：利用训练后的lstm模型对行人位置进行预测，得到第t时刻行人的位置为(hxt,hyt)；

步骤5：对步骤3和步骤4中计算出的行人位置进行卡尔曼滤波融合，完成对行人的定位：

步骤5.1：将步骤4中lstm模型预测出的行人位置(hxt,hyt)作为状态向量xt，构建行人定位的状态方程为

xt＝axt-1+but+wt

步骤5.2：将步骤3中行人运动模型估算出的行人位置(xt,yt)作为观测向量zt，构建行人定位的观测方程为

zt＝stxt+vt

其中，a为状态转移矩阵，a、b均为常数矩阵，ut为控制量，wt、vt分别为第一噪声向量、第二噪声向量，st为观测矩阵；

步骤5.3：估计第t时刻行人位置的状态变量为

步骤5.4：计算第t时刻行人位置的协方差为

pt^-＝apt-1a^t+r

其中，r为常数矩阵；

步骤5.5：计算第t时刻行人位置的卡尔曼滤波增益为

kt＝pt^-st^t[stpt^-st^t+r]^-1

步骤5.6：用第t时刻行人位置的观测量对第t时刻行人位置的估计量进行修正，得到第t时刻行人位置的最优估计值为

将作为行人在第t时刻的最终位置；

步骤5.7：更新协方差为：

pt＝[i-ktst]pt^-

其中，i为单位矩阵。

所述步骤1中，对数据集进行预处理包括：对数据集进行去噪处理以过滤奇异点后进行均值滤波处理。

本发明的有益效果为：

(1)本发明基于lstm和多传感器融合对行人进行室内定位，利用lstm提高了地磁序列匹配的精度，利用卡尔曼滤波让算法适用于更多的场景，且定位精度达到平均1.5m，适用范围广，定位时间短。

(2)本发明不需要借助任何额外设备，只需要智能手机就能够实现在室内环境下行人的定位服务，成本低、容易部署，且能够取得更高的定位精度。

附图说明

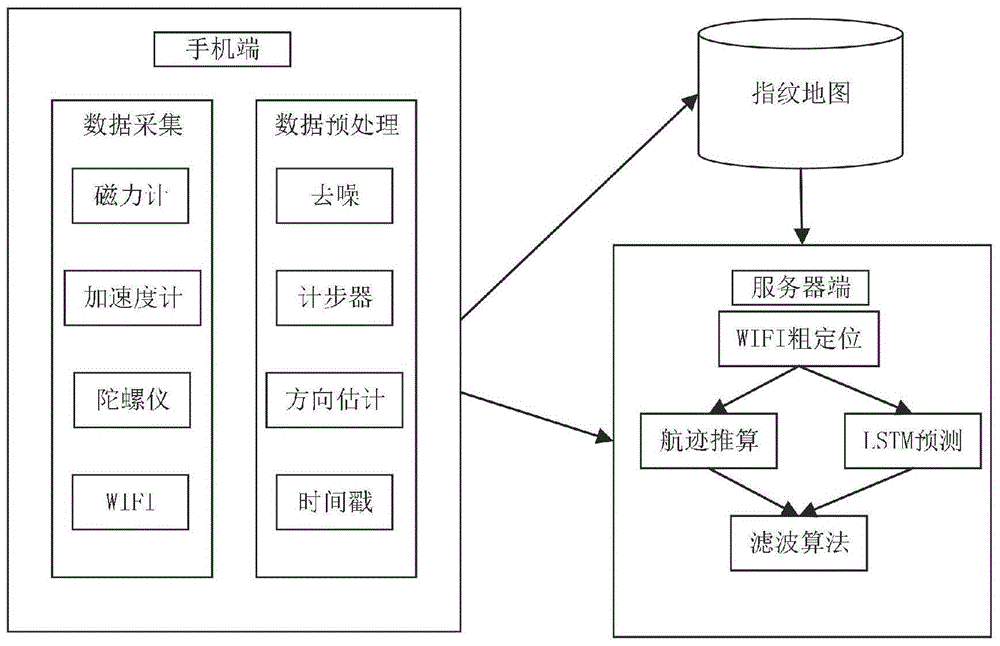
图1为本发明基于lstm和多传感器融合的室内定位方法的流程图；

图2为本发明实施例中对楼层进行划分的示意图；

图3为本发明实施例中地磁指纹的三维效果图；

图4为本发明实施例中行人运动模型的结构示意图；

图5为本发明实施例中不同步长的加速度曲线图；

图6为本发明实施例中实际步长与预测步长的对比图；

图7为地球坐标系的示意图；

图8为手机坐标系的示意图；

图9为本发明实施例中行人运动模型和smartpdr模型对空旷的大厅中行人定位的误差对比图；

图10为本发明实施例中行人运动模型和smartpdr模型对走廊中行人定位的误差对比图；

图11为本发明实施例中行人运动模型和smartpdr模型对实验室中行人定位的误差对比图；

图12为本发明实施例中行人运动模型和smartpdr模型对教室中行人定位的误差对比图；

图13为本发明行人定位的lstm模型的结构示意图；

图14为本发明行人定位的lstm模型的计算结构示意图；

图15为本发明行人定位的lstm模型的参数计算过程示意图；

图16为实施例中不同场景中lstm模型的定位精度对比图；

图17为实施例中不同场景中lmsloc的定位精度对比图；

图18为实施例中走廊场景下本发明基于lstm和多传感器融合的室内定位方法和其他方法的定位精度对比图；

图19为实施例中大厅场景下本发明基于lstm和多传感器融合的室内定位方法和其他方法的定位精度对比图；

图20为实施例中本发明基于lstm和多传感器融合的室内定位方法和其他方法的定位时间对比图。

具体实施方式

下面将结合附图和具体实施方式，对本发明作进一步描述。

如图1所示，为本发明基于lstm和多传感器融合的室内定位方法的流程图。本发明的基于lstm和多传感器融合的室内定位方法，其特征在于，包括下述步骤：

步骤1：使待定位的行人配置手机，通过手机的加速度计、地磁传感器、陀螺仪，以采样频率f分别采集行人在第t时刻的三轴加速度at＝[axt,ayt,azt]^t、三轴磁力值mt＝[mxt,myt,mzt]^t、三轴角速度ωt＝[wxt,wyt,wzt]^t，采集行人在第t时刻的位置坐标(posxt,posyt)，形成数据集，并将数据集传输给计算机，利用计算机对数据集进行预处理；其中，t∈{1,2,...,n}，n为一个行走周期中采集的样本总数。

所述步骤1中，对数据集进行预处理包括：对数据集进行去噪处理以过滤奇异点后进行均值滤波处理。

本实施例中，使待定位的行人配置的手机为android智能手机。分别配置两种手机，进行两组定位。一部是小米6，另一部是三星galaxys8，选两部手机的目的是为了分析不同手机之间的相关数据的差别，采集数据集时用的是三星galaxys8，小米6作为比较。不同手机的采集频率不同，因此延迟也不同，延迟越高，处理器的负载越小，耗电越少。处理数据的计算机采用windows10系统，用来处理数据的语言是python3，开发工具是pycharm。lstm模型选择的实现库是keras。

本实施例中，手机端采集数据并进行数据预处理，采集到的数据在计算机中的表示如表1所示。

表1

步骤2：利用wifi信息对行人进行粗定位：

步骤2.1：在离线阶段，建立行人位置和指纹之间的对应关系：按室内结构对每个楼层进行划分，对所有房间和走廊进行编号并将每个房间作为一个网格、将走廊划分成多个网格，在每个网格中随机选取多个采样点；利用wifi传感器采集在每个采样点上手机能连接到的ap的rss构成位置指纹，并记录ap的id及该采样点对应的房间编号或走廊编号，构建wifi指纹库；

步骤2.2：在在线阶段，在wifi指纹库中利用欧氏距离找到与当前行人手机接收到的ap的rss最近的指纹，并利用三角定位法，计算出行人的初始位置(x0,y0)。

本实施例中，如图2所示，对楼层进行划分。对走廊中一个6m*10m区域形成的地磁指纹如图3所示，x、y轴的数据代表平面坐标，z轴数据表示的是该点的地磁模值数据。

步骤3：利用三轴加速度数据对行人进行计步并进行步长估计，利用三轴磁力值数据和三轴角速度数据对行人进行方向估计，形成如图4所示的行人运动模型，并结合wifi粗定位获得的初始位置，对行人位置进行估算：

步骤3.1：采用滑动窗口方式，利用当前时间窗口内的三轴加速度数据对行人进行计步：计算第t时刻的步行参数为

若vat＝1，则第t时刻行人走了一步；若vat＝0，则第t时刻行人未走一步；其中，accelow、accehigh分别为加速度峰值的下限、上限，δt为两个相邻步的时间间隔，tlow、thigh分别为两个相邻步的时间间隔的下限、上限。

其中，通过滑动窗口的方式来处理加速度数据，滑动窗口相当于一个加速度数据缓存区，加速度传感器不断地向缓存区输入实时的加速度三轴数据的模值，当一个窗口填满，就启动一个线程对该窗口的数据进行计步。

手机的姿态不是固定的，因此计步算法使用的是加速度传感器三个轴数据的模值。但是传感器本身包含许多噪声，而且行人走路过程中手机本身也会有抖动，也就是说不是所有的波峰和波谷都是走路造成的。例如微信和支付宝的步数记录，频繁地摇动手机步数就会增加，实际定位中这种情况是必须要考虑到的，所以在计步之前，先对原始的加速度数据进行去噪，过滤掉这些伪波峰或波谷。行人步行的时候两个相邻步之间是有时间间隔的，步行速度快则时间间隔短，步行速度慢则时间间隔长。人类能够达到的最快的跑步频率为5hz，也就是说人类的极限是1秒跑5步，相当于1步0.2秒，也就是说相邻两步的时间间隔不能小于0.2秒。同样，波峰和波谷也就是加速度模值的峰值也在一定的范围内。

本实施例中，accelow＝g，accehigh＝2g，tlow＝200毫秒，thigh＝2000毫秒，在不同情况下的计步效果如下表2所示。行人直走30步时，计步算法的准确率为100％，因为这时行人一直保持着一个姿势前进，加速度传感器读数也比较稳定。当行人先直走，然后再转个直角弯，再接着直走时，这时实际步数为60步，计步结果为59步。行人沿着走廊走一圈再回到原地时，经过了三个直角弯，这时出现了5步的偏差。计步算法的平均准确率在98％，能够满足定位需求。

表2

步骤3.2：对行人进行动态步长估计：计算行人的步长为

lt＝αh+βw+γf

其中，h为行人的身高，w为行人的体重，f为步频，f＝f/n，α、β、γ均为参数。

本实施例中，α为0.42，β为0.0006，γ为0.0003。行人的步长受身高影响较大，受体重影响较小。步长与加速度计的读数有相关性，步长越长加速度传感器读数模值的峰值越大，振幅也越大，不同步长的加速度曲线如图5所示。如图6所示，为本实施例中实际步长与预测步长的对比图，显然，步长估计方法取得了不错的效果，行人的步长为80cm，预测误差很小，当行人突然改变步长时，算法也取得了不错的效果。

步骤3.3：利用三轴磁力值数据和三轴角速度数据对行人进行方向估计：

本发明最终给出的行人位置是以地球坐标系为参考的，因此需要对手机坐标系进行转换。地球坐标系与手机坐标系的示意图分别如图7、图8所示。

步骤3.3.1：计算手机的俯仰角θt、横滚角偏航角ψt对应的旋转矩阵分别为

步骤3.3.2：计算手机坐标系到地球坐标系的坐标转换矩阵为

其中，i表示手机坐标系，e表示地球坐标系。俯仰角θt表示手机绕x轴旋转的角度，也就是表示的手机上下摆动，以y轴往z轴方向为正，范围是-180°到180°。横滚角是手机绕y轴旋转产生的角，表示手机的左右旋转，以顺时针方向为正方向，范围是-90°到90°。偏航角ψt，此时手机绕z轴旋转，代表地磁北与y轴的夹角，按照顺时针方向增加，范围是0～360°。

步骤3.3.3：利用三轴角速度数据计算手机的偏航角为ψt1；

陀螺仪无法给出初始方向，这时需要用地磁传感器结合加速度计来计算手机的初始的偏航角，假设初始时手机处于静止状态。

步骤3.3.4：利用三轴加速度数据计算手机的俯仰角θt、横滚角分别为

其中，g为重力加速度；

步骤3.3.5：利用三轴磁力值数据计算手机的偏航角ψt2为

步骤3.3.6：将利用三轴角速度数据计算的偏航角ψt1作为状态向量、将利用三轴磁力值数据计算的偏航角ψt2作为观测向量，进行卡尔曼滤波，得到修正后的偏航角ψt；

定义四元数q＝(q0,q1,q2,q3)，那么用四元数表示的手机姿态其中：

通过卡尔曼滤波来修正偏航角，假设陀螺仪的角速度误差和地磁传感器的误差都是状态变量，都服从高斯分布。将陀螺仪结果作为系统状态，将地磁传感器计算的角度作为系统的观测，然后进行更新协方差矩阵和观测更新，最后将求解的四元数转换为手机的实际方向角。其中，通过陀螺仪采集的数据来校正地磁传感器的磁场干扰，同时地磁传感器可以提供初始方位并且补偿陀螺仪的偏差。不同情况下的方向估计效果如下表3所示，从表3中可以看出，快速转弯的误差最大为3.6°，而转180°的误差为2.9°。这说明经过卡尔曼滤波之后，地磁传感器能有效地修正快速转动时陀螺仪的误差。

表3

步骤3.4：估算第t时刻行人的位置为(xt,yt)；

其中，xt＝xt-1+ltsinψt，yt＝yt-1+ltcosψt。

其中，利用行人运动模型估计行人位置的惯性导航算法如下表4所示。

如图9、图10、图11、图12所示，分别为本实施例中行人运动模型和smartpdr模型对空旷的大厅、走廊、实验室、教室中行人定位的误差对比图。可以看出，在空旷的大厅场景中，随着时间的增长，两种方法的误差逐渐增大，这是累计误差引起的，因为每一步的步长的估计和方向的估计都存在一定的噪声，这个噪声在行人走路的过程中逐渐增大。但是本发明lmsloc提出的行人运动模型的增长趋势明显比smartpdr要低，在15米的时候，smartpdr的误差已经达到了3米多，而lmsloc的误差在1m多，这说明短时间内行人运动模型的精度是值得信赖的。在其他几个场景中，lmsloc的表现效果都比smartpdr要好。

表4

步骤4：构建并训练行人定位的lstm模型，利用训练后的lstm模型对行人位置进行预测：

由于行人的走路方式多种多样，单一的指纹地图并不能包含这种特性。而本发明需要的是泛化能力强且适应多种场景的模型。采集到的多个指纹地图是平行的结构，因此需要将这些数据合并处理，因此需要选择多序列并行的lstm(longshort-termmemory，长短期记忆网络)结构来解决这一问题。

步骤4.1：用行人在第t时刻的三轴磁力值的模值mt及位置坐标(posxt,posyt)构建训练数据集in＝{in1,in2,...,int,...,inn}；

其中，int＝(mt,pt)，pt＝(posxt,posyt)；

设计好lstm的整体结构后，要进行参数的设置，首先需要定义输入和输出数据，每一个地磁指纹都包括地磁传感器的三轴读数的模值及对应的室内位置的横纵坐标。如图13所示，为本发明行人定位的lstm模型的结构示意图。其中，学习系统由训练数据学习一个预测器y＝f(mt)；预测系统通过学习到的lstm模型对于新的输入实例mt+1进行预测，即预测其输出的位置pt+1。

如图14、图15所示，分别为本发明行人定位的lstm模型的计算结构、参数计算过程示意图。

步骤4.2：设定lstm模型的输出的激活函数为tanh函数、三个门的激活函数均为sigmoid函数σ；

其中，tanh函数能够避免出现梯度消失问题，因为它的二阶导数在趋近零点之前能维持很长距离。sigmoid函数可以将输出压缩到0和1之间，当sigmoid值为0时，任何信息都不能通过，反之，sigmoid值为1时，任何信息都能通过，因此该函数可以用来控制忘记或者记住信息，所以设置lstm模型的三个门的激活函数都为sigmoid函数。

步骤4.3：利用训练数据集，对lstm模型进行训练：

步骤4.3.1：计算遗忘门的输出为

ft＝σ(wf[ht-1,int]+bf)

其中，ht-1为上一时刻lstm模型的输出，wf为遗忘门的权重，wf由ht-1的权重和int的权重构成，bf为遗忘门的偏置；

遗忘门读取上一时刻模型的输出和当前时刻模型的输入，再乘上sigmoid激活函数，决定遗忘多少信息。记忆单元包含上一时刻的地磁数据和对应的位置，计步算法判断是否行人走了一步，然后lstm模型决定是否要忘记上一时刻的信息。

步骤4.3.2：计算输入门的输出为

it＝σ(wi[ht-1,int]+bi)

利用tanh激活函数建立新的候选向量为

更新记忆单元为

其中，wi为输入门的权重，bi为输入门的偏置；

输入门负责决定地磁数据是否要存入到记忆单元中，首先，sigmoid层决定什么值将要更新，在地磁序列模型中，要增加新的地磁数据到记忆单元中，来替代旧的需要忘记的数据；然后，tanh激活函数建立一个新的候选向量，并将其被加入到记忆单元中。这时就完成了记忆单元的更新，记忆单元ct-1更新为新的状态ct，将长期记忆与遗忘门相乘，丢弃需要丢弃的信息，将当前记忆与输入门相乘，选择需要保留的信息，然后将两部分相加，这样就完成了一次数据的更新。遗忘门负责保存很久之前的信息，输入门避免不相关的信息进入记忆。

步骤4.3.3：计算输出门的输出为

ot＝σ(wo[ht-1,int]+bo)

利用tanh激活函数控制记忆单元，得到lstm模型在第t时刻的输出为

其中，wo为输出门的权重，bo为输出门的偏置；

其中，先通过激活函数来确定哪个部分将被输出，然后通过tanh控制记忆单元，二者相乘，共同决定lstm当前时刻的输出ht。

步骤4.4：沿时间方向的反向传播过程，对lstm模型进行训练：

步骤4.4.1：定义目标函数为

定义第t时刻lstm模型的误差项为

其中，为行人位置的预测坐标；

优化算法的目的就是找到是目标函数最小的参数值。

步骤4.4.2：计算遗忘门、输入门、输出门、候选向量的加权输入分别为

netf,t＝wf[ht-1,int]+bf＝wfhht-1+wfinint+bf

neti,t＝wi[ht-1,int]+bi＝wihht-1+wiinint+bi

neto,t＝wo[ht-1,int]+bo＝wohht-1+woinint+bo

得到遗忘门、输入门、输出门、候选向量加权输入的误差项分别为

计算第t-1时刻lstm模型的误差项为

利用全导数公式可得

计算lstm模型沿时间方向反向传播到第k时刻的误差项为

其中，是一个n*n的矩阵，n是隐层的维度。

步骤4.4.3：将误差项向上一层传播，假设当前为第l层，定义第l-1层的误差项是目标函数对第l-1层加权输入的导数

计算第l层的输入为

其中，f^l-1为第l-1层的激活函数；

利用全导数公式将误差传递到上一层为

计算第t时刻遗忘门的梯度为

将各时刻梯度加一起，得到第t时刻遗忘门权重的梯度为

步骤4.5：利用训练后的lstm模型对行人位置进行预测，得到第t时刻行人的位置为(hxt,hyt)。

lstm模型训练结果显示，在复杂场景的定位精度在1m左右，但是在稍显空旷的场景精度就会降低。实验证明行人运动模型的短时间内精度是准确的，受环境影响较小。因此在空旷场景下，利用卡尔曼滤波算法将lstm模型预测的结果和行人运动模型的结果进行整合，用行人运动模型的结果来不断修正lstm模型预测的误差。

步骤5：对步骤3和步骤4中计算出的行人位置进行卡尔曼滤波融合，完成对行人的定位：

步骤5.1：将步骤4中lstm模型预测出的行人位置(hxt,hyt)作为状态向量xt，构建行人定位的状态方程为

xt＝axt-1+but+wt

其中，在lstm预测模型中，第t时刻的系统状态是与上一时刻t-1密切相关的，因为lstm网络本身处理的就是时序数据。

步骤5.2：将步骤3中行人运动模型估算出的行人位置(xt,yt)作为观测向量zt，构建行人定位的观测方程为

zt＝stxt+vt

其中，a为状态转移矩阵，a、b均为常数矩阵，ut为控制量，wt、vt分别为第一噪声向量、第二噪声向量，st为观测矩阵；

其中，观测方程定义了行人运动模型的计算结果与系统当前时刻的状态也即lstm模型的结果的关系。

预测过程中把lstm网络的预测值作为先验信息，然后通过行人运动模型来更新lstm网络的预测值。

步骤5.3：估计第t时刻行人位置的状态变量为

步骤5.4：计算第t时刻行人位置的协方差为

pt^-＝apt-1a^t+r

其中，r为常数矩阵；

用上一时刻的状态预测当前的状态，用上一时刻的状态的协方差预测当前的协方差，这是系统状态的时间更新。

步骤5.5：计算第t时刻行人位置的卡尔曼滤波增益为

kt＝pt^-st^t[stpt^-st^t+r]^-1

其中，卡尔曼滤波增益其实是系统状态估计值的方差和运动模型的方差的比值，因此上一时刻系统状态的估计值对卡尔曼增益的大小起决定性作用，也就是说上一时刻lstm模型的估计值方差很大，那么说明上一时刻的估计不准确，导致卡尔曼增益也很大，更接近1，因此导致行人运动模型的观测值所占的比例就会更大，当前时刻算法更信赖行人运动模型的测量值，这时在最终算法提供的位置信息中，行人运动模型所占的比例大，这样就可以修正空旷场景下lstm预测不准确的问题。

步骤5.6：用第t时刻行人位置的观测量对第t时刻行人位置的估计量进行修正，得到第t时刻行人位置的最优估计值为

将作为行人在第t时刻的最终位置；

步骤5.7：更新协方差为：

pt＝[i-ktst]pt^-

其中，i为单位矩阵。

上述卡尔曼滤波融合方法自回归地运行下去，使得估计值一步步逼近真实值，算法最终计算的位置会更准确。

为了检验卡尔曼滤波融合的效果，本实施例中，将lstm模型在不同场景中的定位效果与本发明的方法lmsloc中卡尔曼滤波融合后的定位效果进行对比，如图16、图17所示。图中，cdf为累积分布函数。从图16中可以看出，lstm在复杂场景例如实验室表现最好，其次是教室和走廊，在大厅定位效果稍差。因为其他三个场景中的每个场景都比大厅结构复杂。实验室过道窄，且台式电脑很多，地磁环境被扭曲程度大，教室和走廊的宽度相差不多，而且走廊一侧靠墙，受钢筋影响，扭曲程度大，而大厅就相对比较空旷了，除了一个柱子没有别的东西，地磁变化率不明显。从图17可以看出，本发明的方法lmsloc中卡尔曼滤波融合后，在空旷场景，定位精度有了明显的提高，这是因为融合了惯性导航的原因，在这种情况下，地磁变化率不明显，卡尔曼滤波会给惯性导航的结果一个更大的权重，这时行人运动模型在定位过程中发挥主要作用。本发明可以得出结论，越复杂的建筑结构可能会导致严重的磁变形这意味着产生更好的指纹。

为了检验本发明基于lstm和多传感器融合的室内定位方法lmsloc和其他定位方法的优劣，选择了其他三个方法进行对比实验，分别是基于粒子滤波和地磁指纹的maloc、smartpdr、基于wifi的wiloc，在同一场景下评估不同算法的定位精度，分别是走廊和大厅，定位结果如图18、图19所示。结果表明，lmsloc的定位精度表现更好。虽然lmsloc和粒子滤波算法maloc表现出几乎相同的精度，但是相较于wiloc和smartpdr，lmsloc的定位精度明显更令人满意。

如图20所示，为本发明基于lstm和多传感器融合的室内定位方法和其他方法的定位时间对比图。其中，图20为定位时间复杂度的盒图形式，x轴表示选取的方法，y轴表示算法运行的时间。在定位时效性方面，粒子滤波本来就是使用的蒙特卡洛的思想，如果粒子数量过高，那么就会大大影响算法的效率。从图15中也可以清楚地看出，smartpdr方法由于其计算的过程都是确定的，时间上所耗费的时间是最短的，而粒子滤波算法maloc随着粒子数的增加，时间的复杂度也在增加。本发明提出的方法lmsloc在时效性方面的表现是远远超过粒子滤波算法maloc的。

显然，上述实施例仅仅是本发明的一部分实施例，而不是全部的实施例。上述实施例仅用于解释本发明，并不构成对本发明保护范围的限定。基于上述实施例，本领域技术人员在没有做出创造性劳动的前提下所获得的所有其他实施例，也即凡在本申请的精神和原理之内所作的所有修改、等同替换和改进等，均落在本发明要求的保护范围内。