一种地球同步轨道星机双基合成孔径雷达大幅宽成像方法与流程

本发明属于合成孔径雷达技术领域，特别涉及一种地球同步轨道星机双基合成孔径雷达大幅宽成像方法。

背景技术：

合成孔径雷达(sar)是一种高分辨成像雷达，具有穿透性强，能全天时、全天候的特点，目前技术已经相较成熟，被广泛应用在地球遥感、资源勘探、地形测绘等领域。

地球同步轨道合成孔径雷达(geosynchronoussyntheticapertureradar,geosar)的轨道高度在36000km左右的同步轨道，其波束对地面的覆盖能达到280km，有着重访周期短，可观测范围广的优势，可在大范围内保持对指定区域的持续照射。

地球同步轨道星机双基合成孔径雷达(geosynchronousspaceborne-airbornebistaticsar,geobisar)以geosar的卫星作为照射源，机载平台作为接收站，是一种新的对地成像的双基sar架构。由于其收发分置，具有双基sar系统配置灵活的特点；并且机载接收站不主动辐射能量，隐蔽性好，发射站在地球同步轨道，生存力强，具有长期、稳定、可靠的成像能力。同时，这种“远发近收”的构型可以获得比单基geosar更高的成像信噪比，并且引入高转角速度的机载平台可以在短时间内积累多普勒带宽保证成像分辨率。

然而，机载接收站受限于高度与最小天线单元面积限制，接收波束覆盖范围一般只能达到几公里级别(3km左右)，这与geosar的波束覆盖范围(280km左右)相差甚远。因此，为了充分利用发射站的覆盖范围，扩大接收站的观测范围，本发明采用tops模式对地面进行多测绘带扫描接收。但是由于一般的geo-bisar的点目标回波多普勒带宽已经超过了发射站的脉冲重复频率(prf)，会导致频谱因欠采样而发生混叠，带来欠采样模糊，现有技术中，针对geobisar的欠采样模糊的多通道技术被提出。而在tops模式下接收到的回波频谱会存在多普勒质心空变，不同方位点目标的频谱占据着不同频段，导致整个场景内的多普勒带宽远远超出prf；另外，还有针对一般tops回波去除旋转模糊的方法。但是这类方法都针对的都是prf大于点目标多普勒带宽的情形，一旦prf低于点目标多普勒带宽，方法将失效，无法进行不模糊的成像。

技术实现要素：

本发明的目的在于解决上述问题，提出了一种地球同步轨道星机双基合成孔径雷达大幅宽成像方法，使用geo卫星作为照射源，在机载接收平台上沿航迹布置多个通道同时进行tops扫描接收回波，然后对接收到的多个通道的回波进行处理，去除欠采样模糊，再解决旋转模糊，抑制了geo星机双基sar在采用tops模式接收回波时的频谱模糊，实现了geo星机双基sar回波的无模糊成像。

一种地球同步轨道星机双基合成孔径雷达大幅宽成像方法，包括以下步骤：

s1、n个通道同时对子测绘带录取回波，第m个通道的基带回波信号为sechom(τ,η)，其中，τ和η分别表示距离向时间和方位向时间；

s2、对多通道的基带回波信号进行多通道重构，得到无欠采样模糊的回波频谱；

s3、对所述回波频谱进行去旋转模糊；

s4、对回波信号进行聚焦处理；

s5、进行去方位时域混叠，得到所述子测绘带的一次burst图像；

s6、将得到的多个子测绘带的burst图像进行拼接，获得宽测绘带sar图像，完成大幅宽成像。

进一步地，所述步骤s1包括：

发射线性调频信号，n个通道同时对子测绘带录取回波，进行解调得到基带回波信号，第m个通道的基带回波信号为

其中，wr(·)和wa(·)分别表示距离向和方位向的窗函数，rect(·)表示矩形窗函数，rm(η)表示第m个通道的双基距离和历史，表示波束中心穿越目标的时刻，旋转系数τ和η分别表示距离向时间和方位向时间，c表示光速，j表示虚数单位，r0表示目标点到接收站航迹的垂直距离，td表示波束驻留时间，tb表示一次burst的时间，kr表示发射信号的调频率，vf表示波束脚印的速度，vr表示平台速度，ωrot表示扫描旋转角速度，λ表示中心波长，c和f0分别表示光速和sar发射脉冲载频。

进一步地，其特征在于，所述步骤s2包括：

s21、对所述步骤s1得到的每个通道的基带回波信号进行质心去斜，即相位相乘

sderampm(τ,η)＝sechom(τ,η)exp(-jπkdcη²)

其中，kdc为多普勒质心随方位时间变化的斜率，

s22、构造第m个通道相对于参考通道的差异函数

其中，δxm表示第m个通道到参考通道的距离，fη表示方位频率，k1t表示发射站到目标点的斜距一阶系数；

s23、将hm(fη)在频域平移prf的整数倍的结果作为元素构成系统矩阵

其中，n表示通道数，prf表示脉冲重复频率；

s24、获取所述系统矩阵的逆，得到重构矩阵

s25、将所述步骤s21得到的sderampm(τ,η)进行方位向快速傅里叶变换

srdm(τ,fη)＝fftaz{sderampm(τ,η)}

其中，fftaz{·}表示方位向快速傅里叶变换运算；

s26、将n个通道的基带回波信号经过所述步骤s25的结果排列成矩阵形式

srd(τ,fη)＝[srd1(τ,fη)srd2(τ,fη)…srdn(τ,fη)]

s27、将srd(τ,fη)与所述步骤s24中的p(τ,fη)相乘，完成多通道重构，得到无欠采样模糊的回波频谱

spre(τ,fη)＝srd(τ,fη)·p(τ,fη)

＝(u1(τ,fη)u2(τ,fη+prf)…un(τ,fη+(n-1)prf))

其中，uk(τ,fη),k＝1,2,…n表示重构后的第k个子带频谱，重构后的信号频谱由n个频谱拼接而成，重构后的fη由fη∈[-prf/2,prf/2]转换为fη∈[-n·prf/2,n·prf/2]，等效方位采样率为重构前的n倍，抑制欠采样模糊。

进一步地，所述步骤s3包括：

s31、对spre(τ,fη)进行方位向快速傅里叶变换

sderamp(τ,η)＝ifftaz{sprf(τ,fη)}

s32、对sderamp(τ,η)进行方位向快速傅里叶变换

sp1(τ,η1)＝ifftaz{sderamp(τ,η)}

其中，η1表示所述步骤s32的方位向傅里叶变换后的方位时间，η1∈[-0.5n·prf/kdc,0.5n·prf/kdc]；

s33、对sp1(τ,η1)进行方位向相位相乘

s34、对sp2(τ,η1)进行方位向快速傅里叶变换

sp3(τ,fη1)＝fftaz{sp2(τ,η1)}

其中，fη1表示η1对应的方位频率，fη1∈[-kdctb/2,kdctb/2]；

s35、对sp3(τ,fη1)进行相位相乘

进一步地，所述步骤s4包括：

s41、对secho(τ,fη1)进行距离向快速傅里叶变换

s2df(fτ,fη1)＝fftra{secho(τ,fη1)}

其中，fftra{·}表示距离向快速傅里叶变换运算，fτ表示距离频率；

s42、对s2df(fτ,fη1)进行相位相乘

其中，rt0ref表示burst中心时刻的场景中心到发射站的斜距，rr0ref表示burst中心时刻的场景中心到接收站的斜距；rb0＝rr0ref+rt0ref，其中，k1t和k2t分别表示发射站到目标点的斜距一阶和二阶系数，θst表示接收站的初始斜视角；

s43、对所述步骤s42中相位相乘的结果在距离频率向进行stolt插值，stolt插值过程中距离频率与原距离频率fτ的映射关系为

其中，fτ'表示stolt后的距离频率，rt0表示场景内任意点到发射站的距离，rr0表示场景内任意点到接收站的距离，θe表示场景内任意点的等效斜视角，

s44、对所述步骤s43的结果在方位频率向进行stolt插值，stolt插值过程中方位频率与原方位频率fη1的映射关系为

其中，f′η1表示stolt插值后的方位频率，(xc,yc)表示场景中心点的坐标，(x,y)表示场景内任意点的坐标；

s45、对所述步骤s44的stolt插值的结果进行距离向快速傅里叶变换

sfocus(τ',f′η1)＝ifftra{s'2df(f′τ,f′η1)}

其中，τ'表示fτ'对应的距离向时间，s'2df(f′τ,f′η1)表示所述步骤s44的stolt插值的结果。

进一步地，所述步骤s5包括：

s51、对sfocus(τ',f′η1)进行相位相乘

其中，k'dc表示所述步骤s45完成后的信号多普勒质心变化斜率，rr0表示接收站到场景中心的最近斜距；

s52、对spost1(τ',f′η1)进行方位向快速傅里叶变换

spost1(τ',η′1)＝ifftaz{spost1(τ',f′η1)}

s53、对spost1(τ',η′1)进行相位相乘

spost2(τ',η′1)＝spost1(τ',η′1)exp(jπk'dcη′1²)

s54、对spost2(τ',η′1)进行方位向快速傅里叶变换

spost3(τ',η2)＝fftaz{spost2(τ',η′1)}

其中，η2表示此处方位向快速傅里叶变换的方位时间，η2∈[-0.5tbkdc/k'dc,0.5tbkdc/k'dc]；

s55、对spost3(τ',η2)进行相位相乘

得到子测绘带的一次burst图像。

进一步地，所述步骤s6包括：

依次对各子测绘带执行步骤s1-s5，得到各子测绘带的burst图像，将得到的多个burst图像进行拼接，获得宽测绘带sar图像，完成大幅宽成像。

进一步地，所述步骤s1之前，包括：

初始化系统参数，包括脉冲重复频率、方位向burst采样点数、通道间隔、通道个数、扫描旋转角速度、机载平台速度及地球同步轨道卫星轨道参数。

本发明的有益效果：本发明提供了一种地球同步轨道星机双基合成孔径雷达大幅宽成像方法，本发明根据geo星机双基sar的成像特点，采用在接收站配置多通道并且进行tops扫描多个距离测绘带的手段来录取回波，一方面可以利用多通道技术抑制回波频谱中的欠采样模糊，一方面用two-step和modifiedtwo-step方法处理tops模式下的回波，再结合多个测绘带的数据聚焦出多个测绘带的sar图像，将其拼接后即可得到大幅宽的成像结果。由于本发明使用了多通道技术，对系统的prf要求较低，可以大大减轻geosar发射功率与数据存储的负担。而tops接收模式对多个距离向的测绘带进行扫描，大幅提高了机载接收站的成像范围。

附图说明

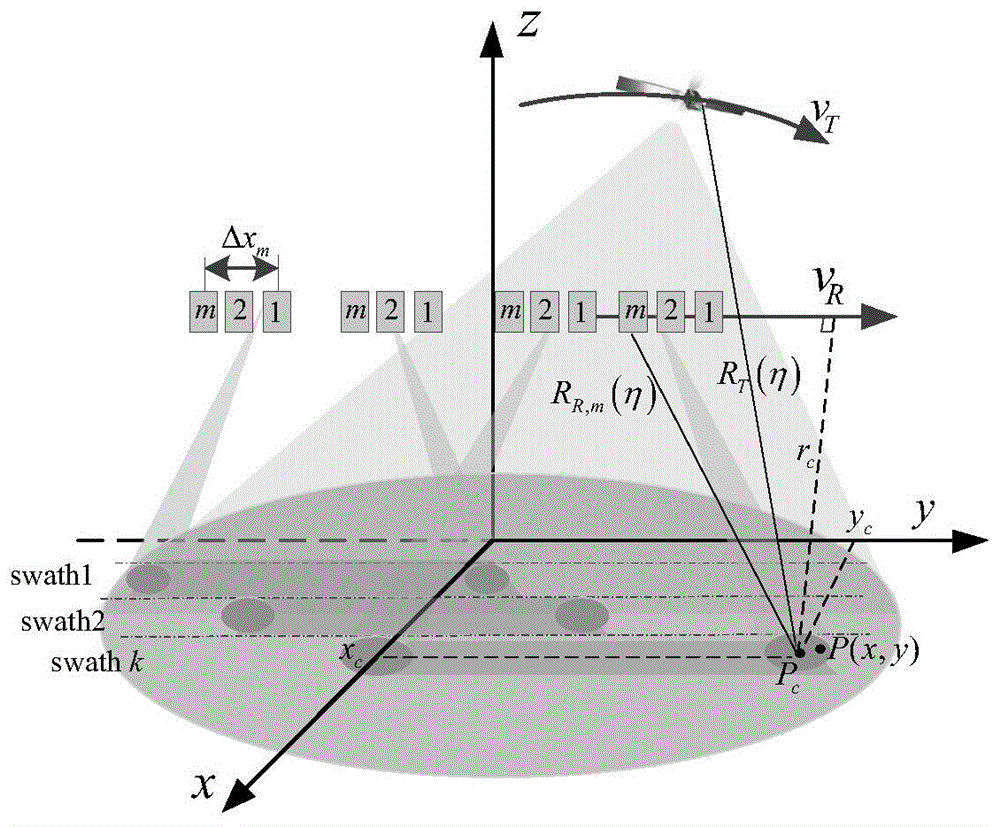
图1为本发明实施例的geo星机双基sar回波录取几何示意图。

图2为本发明实施例的流程图。

图3为本发明实施例的点目标分布示意图。

图4为本发明实施例的大幅宽sar成像结果图。

图5为图4中点目标a的等高图。

图6为图4中点目标b的等高图。

图7为图4中点目标c的等高图。

具体实施方式

下面结合附图对本发明的实施例做进一步的说明。

本发明提出了一种地球同步轨道星机双基合成孔径雷达大幅宽成像方法，地球同步轨道合成孔径雷达(geosynchronoussyntheticapertureradar,geosar)，为一种将sar有效载荷放置在地球同步轨道卫星上的主动式遥感传感器。而geo星机双基sar(geo-bisar)，即地球同步轨道星机双基合成孔径雷达，是双基地sar的一种，是一种以地球同步轨道卫星为发射站，接收站是机载平台的星机双基地sar。

本实施例中，geo星机双基sar几何结构如图1所示，系统参数如下表1所示。

表1geo星机双基sar系统参数表

请参阅图2，本发明通过以下步骤实现：

s1、n个通道同时对子测绘带录取回波，第m个通道的基带回波信号为sechom(τ,η)，其中，τ和η分别表示距离向时间和方位向时间。

本实施例中，发射线性调频信号，n＝4个通道同时对子测绘带进行tops扫描录取回波，进行解调得到基带回波信号，第m个通道的基带回波信号为

其中，m∈(1,2,3,4)，wr(·)和wa(·)分别表示距离向和方位向的窗函数，rect(·)表示矩形窗函数，rm(η)表示第m个通道的双基距离和历史，表示波束中心穿越目标的时刻，旋转系数τ和η分别表示距离向时间和方位向时间，c表示光速，j表示虚数单位，r0表示目标点到接收站航迹的垂直距离，td表示波束驻留时间，tb表示一次burst的时间，kr表示发射信号的调频率，vf表示波束脚印的速度，vr表示平台速度，ωrot表示扫描旋转角速度，λ表示中心波长，c和f0分别表示光速和sar发射脉冲载频。

s2、对多通道的基带回波信号进行多通道重构，得到无欠采样模糊的回波频谱。

本实施例中，步骤s2通过以下子步骤实现：

s21、对步骤s1得到的每个通道的基带回波信号进行质心去斜，即相位相乘

sderampm(τ,η)＝sechom(τ,η)exp(-jπkdcη²)

其中，kdc为多普勒质心随方位时间变化的斜率，

s22、构造第m个通道相对于参考通道的差异函数

其中，δxm表示第m个通道到参考通道的距离，fη表示方位频率，k1t表示发射站到目标点的斜距一阶估计系数。

s23、将hm(fη)在频域平移prf的整数倍的结果作为元素构成系统矩阵

其中，n表示通道数，prf表示脉冲重复频率。

s24、获取s23中系统矩阵的逆，得到重构矩阵

s25、将步骤s21得到的sderampm(τ,η)进行方位向快速傅里叶变换

srdm(τ,fη)＝fftaz{sderampm(τ,η)}

其中，fftaz{·}表示方位向快速傅里叶变换运算。

s26、将n＝4个通道的基带回波信号经过步骤s25的结果排列成矩阵形式

srd(τ,fη)＝[srd1(τ,fη)srd2(τ,fη)…srd4(τ,fη)]

s27、将s26的结果srd(τ,fη)与步骤s24中的p(τ,fη)相乘，完成多通道重构，得到无欠采样模糊的回波频谱

spre(τ,fη)＝srd(τ,fη)·p(τ,fη)

＝(u1(τ,fη)u2(τ,fη+prf)…u4(τ,fη+3prf))

其中，uk(τ,fη),k＝1,2,…4表示重构后的第k个子带频谱，重构后的信号频谱由n＝4个频谱拼接而成，重构后的fη由fη∈[-prf/2,prf/2]转换为了fη∈[-4·prf/2,4·prf/2]，等效方位采样率为重构前的n＝4倍，欠采样模糊得到了有效抑制。

s3、对回波频谱进行去旋转模糊。

本实施例中，步骤s3通过以下子步骤实现：

s31、对s27的结果spre(τ,fη)进行方位向快速傅里叶变换

sderamp(τ,η)＝ifftaz{sprf(τ,fη)}

s32、对s31的结果sderamp(τ,η)进行方位向快速傅里叶变换

sp1(τ,η1)＝ifftaz{sderamp(τ,η)}

其中，η1表示该步骤s32的方位向傅里叶变换后的方位时间，η1∈[-0.5n·prf/kdc,0.5n·prf/kdc]；

s33、对s32的结果sp1(τ,η1)进行方位向相位相乘

s34、对s33的结果sp2(τ,η1)进行方位向快速傅里叶变换

sp3(τ,fη1)＝fftaz{sp2(τ,η1)}

其中，fη1表示η1对应的方位频率，fη1∈[-kdctb/2,kdctb/2]，tb表示一次burst的时间。

s35、对s34的结果sp3(τ,fη1)进行相位相乘

s4、对回波信号进行聚焦处理。

本实施例中，步骤s4通过以下子步骤实现：

s41、对s35中的相位相乘结果secho(τ,fη1)进行距离向快速傅里叶变换

s2df(fτ,fη1)＝fftra{secho(τ,fη1)}

其中，fftra{·}表示距离向快速傅里叶变换运算，fτ表示距离频率。

s42、对s41的结果s2df(fτ,fη1)进行相位相乘

其中，rt0ref表示burst中心时刻的场景中心到发射站的斜距，rr0ref表示burst中心时刻的场景中心到接收站的斜距；rb0＝rr0ref+rt0ref，其中，k1t和k2t分别表示发射站到目标点的斜距一阶和二阶估计系数，θst表示接收站的初始斜视角。

s43、对s42中相位相乘的结果在距离频率向进行stolt插值，stolt插值过程中新距离频率与原距离频率fτ的映射关系为

其中，fτ'表示stolt后的新距离频率，rt0表示场景内任意点到发射站的距离，rr0表示场景内任意点到接收站的距离，θe表示场景内任意点的等效斜视角，

s44、对步骤s43的结果在方位频率向进行stolt插值，stolt插值过程中新方位频率与原方位频率fη1的映射关系为

其中，f′η1表示stolt插值后的新方位频率，(xc,yc)表示场景中心点的坐标，(x,y)表示场景内任意点的坐标。

s45、对步骤s44的stolt插值的结果进行距离向快速傅里叶变换

sfocus(τ',f′η1)＝ifftra{s'2df(f′τ,f′η1)}

其中，τ'表示fτ'对应的距离向时间，s'2df(f′τ,f′η1)表示步骤s44的stolt插值的结果。

s5、进行去方位时域混叠，得到子测绘带的一次burst图像。

本实施例中，步骤s5通过以下子步骤实现：

s51、对s45的结果sfocus(τ',f′η1)进行相位相乘

其中，k'dc表示步骤s45完成后信号的多普勒质心变化斜率，rr0表示接收站到场景中心的最近斜距；

s52、对s51的结果spost1(τ',f′η1)进行方位向快速傅里叶变换

spost1(τ',η′1)＝ifftaz{spost1(τ',f′η1)}

s53、对s52的结果spost1(τ',η′1)进行相位相乘

s54、对s53的结果spost2(τ',η′1)进行方位向快速傅里叶变换

spost3(τ',η2)＝fftaz{spost2(τ',η′1)}

其中，η2表示此处方位向快速傅里叶变换的方位时间，η2∈[-0.5tbkdc/k'dc,0.5tbkdc/k'dc]。

s55、对s54的结果spost3(τ',η2)进行相位相乘

得到子测绘带的一次burst图像。

s6、将得到的多个子测绘带的burst图像进行拼接，获得宽测绘带sar图像，完成大幅宽成像。

本实施例中，依次对各子测绘带执行步骤s1-s5，得到各子测绘带的burst图像，将得到的多个burst图像进行拼接，获得宽测绘带sar图像，完成大幅宽成像。

图3为点目标分布示意图。如图4-7所示为本发明实施例中点目标的结果图。图4为3个测绘带拼接而成的大幅宽sar图像；图5为图4中点目标a的等高图；图6为图4中点目标b的等高图；图7为图4中点目标c的等高图。

本领域的普通技术人员将会意识到，这里的实施例是为了帮助读者理解本发明的原理，应被理解为本发明的保护范围并不局限于这样的特别陈述和实施例。本领域的普通技术人员可以根据本发明公开的这些技术启示做出各种不脱离本发明实质的其它各种具体变形和组合，这些变形和组合仍然在本发明的保护范围内。