基于任务完成时间最小化的多无人机路径规划方法与流程
本发明属于无人机路径规划领域,具体为一种基于任务完成时间最小化的多无人机路径规划方法。
背景技术:
无人机路径规划是实现无人机自主飞行的关键技术保障,路径规划方法则是路径规划的核心。无人机路径规划是指在综合考虑无人机到达时间、油耗、威胁以及飞行区域等因素的前提下,为无人机规划出最优或者满意的飞行路径,以保证圆满地完成飞行任务,并安全返回基地。在20世纪60年代,学者开始研究单架无人机的路径规划技术,70至80年代研究者们受到了机器人领域一些思想的启发,无人机在90年代以后发展迅速,应用领域变得更加广泛,无人机执行的任务也是多种多样。单无人机路径规划方法按照规划决策一般可以分为传统经典算法和现代智能算法。传统优化算法不少都属于凸优化范畴,有唯一明确的全局最优点。很多单无人机路径规划问题都采用凸优化的办法进行解决。现代智能算法大致可以分为五类算法:进化类算法(遗传算法、差分进化算法、免疫算法),群智能算法(蚁群算法、粒子群算法),模拟退火算法,紧急搜索算法,神经网络算法。
如今,随着任务多样化和复杂化,多无人机协同执行任务具有很大的优势。一方面,可以通过任务的同步执行以提高执行效率,缩短完成时间;另一方面,多无人机可以增加任务成功的概率。事实上,多无人机路径规划需要解决任务分配和路径优化两个子问题。现有的路径规划方法大多分开解决这两个子问题。先将任务分配给每架无人机,然后无人机根据分配的任务利用单架无人机路径规划方法得到优化的路径。这种方法没有考虑无人机之间的任务协同,只是单纯将多无人机路径规划方法分解为多个子问题。除此之外,现有的一些算法虽然考虑同时优化这两个问题,但是没有考虑到每架无人机的能耗限制。大多数都是从总能耗和总任务完成时间的角度出发优化,这样容易造成单架无人机负荷过大的后果。
技术实现要素:
本发明的目的在于提供一种基于任务完成时间最小化的多无人机路径规划方法。
实现本发明目的的技术方案为:一种基于任务完成时间最小化的多无人机路径规划方法,包括以下步骤:
步骤1、设定多无人机飞行约束条件和需要满足的信息采集任务要求;
步骤2、根据基站覆盖原理以及设定的信息采集任务要求,确定无人机在信息采集任务过程中的悬停点;
步骤3、根据设计的悬停点和飞行约束条件,利用最小-最大路径覆盖算法,规划每架无人机的路径,完成信息采集任务的分配;
步骤4、基于规划的无人机路径,对飞行时间和信息采集时间进行优化分配,得到最终的无人机轨迹。
优选地,步骤1设定的多无人机飞行约束条件和信息采集任务要求具体为:
式中,li(0)表示无人机i的初始位置,li(t)表示无人机i的最终位置,
||li(t)||是无人机i在t时刻的速度,vmax是无人机最大速度;||li(t)-li'(t)||表示无人机i与i'之间的距离,dmin表示无人机之间保证避碰的最小距离;r表示无人机投影在地面的最大通信半径,||li′(t)-cj′||表示无人机i地面投影点与传感器j之间的距离。
优选地,步骤2根据基站覆盖原理以及设定的信息采集任务要求,确定无人机在信息采集任务过程中的悬停点,具体如下:
步骤2.1、将x定义为已经被覆盖的传感器集合,初始化为空集合;将y定义为未被覆盖的传感器集合,初始化为传感器集合p;将v定义为悬停点集合,初始化为空集合;
步骤2.2、利用凸包的计算方法计算y集合中边界传感器,将其存在ybo集合中,y集合中剩余传感器存在yin集合中;
步骤2.3、随机选择ybo集合中一个传感器b0,并且将ybo集合中与b0的距离在2r范围内的传感器存在集合ρ中,r是无人机在地面上的最大通信半径;
步骤2.4、利用选址问题中寻找中心位置的算法,找到可以覆盖ρ中所有传感器的悬停位置hm,并计算ρ中所有传感器与hm的距离,记录下最大距离d;
步骤2.5、比较d与r的大小关系,若d>r,删除ρ中距离hm最远的点;
步骤2.6、重复步骤2.4-2.5,直到d≤r;
步骤2.7、将yin集合中与hm的距离在r范围以内的传感器存入ρ集合,距离在[r,2r]范围内的传感器存入θ集合中;
步骤2.8、在θ中找到距离hm最近的点b′,把b′从θ中删除,并将其添加到ρ集合中,重复步骤2.4,得到悬停位置hm和最大距离d;
步骤2.9、判断最大距离d与通信半径r的关系。如果d≤r,返回步骤2.8,直到θ集合为空集合;如果d≥r,将b′从ρ中删除,执行步骤2.10;
步骤2.10、更新x,y,v集合,其中x=x∪ρ,y=y/ρ,v=v∪hm;
步骤2.11、重复步骤2.2~2.10,直到所有传感器被覆盖,即y集合为空集合。
优选地,步骤3中利用最小-最大路径覆盖算法,分配规划每架无人机的路径的具体步骤为:
步骤3.1、利用旅行商问题的算法计算一条覆盖所有悬停点的无人机路径;
步骤3.2、只考虑悬停时收集信息的情形,计算无人机在悬停点vm执行信息采集任务需要的悬停时间h(vm)、在悬停点之间飞行所需要的飞行时间w(vm,vm+1)以及总时间w(c);
步骤3.3、计算路径分解向量b=(b1,...,bi,...,bk),其中
步骤3.4、根据步骤3.1得到的路径,建立悬停点和路径的组合序列ve=(ve0=v0,ve1=e(v0,v1),ve2=v1,ve3=e(v1,v2),...,ve2n+1=v0),其中vm表示悬停点,e(vm,vm+1)表示悬停点vm和vm+1之间的路径;
步骤3.5、悬停点和路径的子序列(veo,ve1,...,vej(i))的总权重为wh(veo,ve1,ve2,ve3,...,vej(i))=h(ve0)+w(ve1)+h(ve2)+w(ve3)+....+h(vej(i))/w(vej(i)),其中h(ve2m)为悬停时间,w(ve2m+1)为飞行时间;
步骤3.6、根据判定条件wh(veo,ve1,...,vej(i))≤bi,在ve序列中寻找路径分界点vej(i),1≤i≤k;
步骤3.7、如果路径分界点vej(i)是边,则将该边删除,vej(i)=vej(i)-1作为无人机i初始路径的终点,ve′j(i)=vej(i)+1作为无人机i+1初始路径的起点;
步骤3.8、如果路径分界点vej(i)是点,则vej(i)=vej(i)-2作为无人机i初始路径的终点,ve′j(i)=vej(i)作为无人机i+1初始路径的起始点;
步骤3.9、重复步骤3.6~3.8,直到i=k,得到k架无人机的初始路径c={c1,...,ci,...,ck},其中ci为无人机i的初始路径,即ci=(ve′j(i-1),...,vej(i));
步骤3.10、将初始路径加上无人机从起点飞行到任务区域的路径,构成k架无人机的闭合路径。
优选地,步骤4基于规划的无人机路径,对飞行时间和信息采集时间进行优化分配,得到最终的多无人机路径的具体方法为:
将无人机路径离散化,分成zi段,每段路径长度为
式(8)中,
本发明与现有技术相比,其显著优点为:本发明以最小化用时最长的无人机的任务完成时间为目标,将多无人机路径规划问题转化为悬停点选择以及信息采集任务的分配,高效合理的规划无人机轨迹,降低了任务完成时间,提高了信息采集任务的速率;本发明利用公平性原则的算法来对无人机路径进行规划,最小化任务完成时间从而保证信息采集任务的完成效率。
附图说明
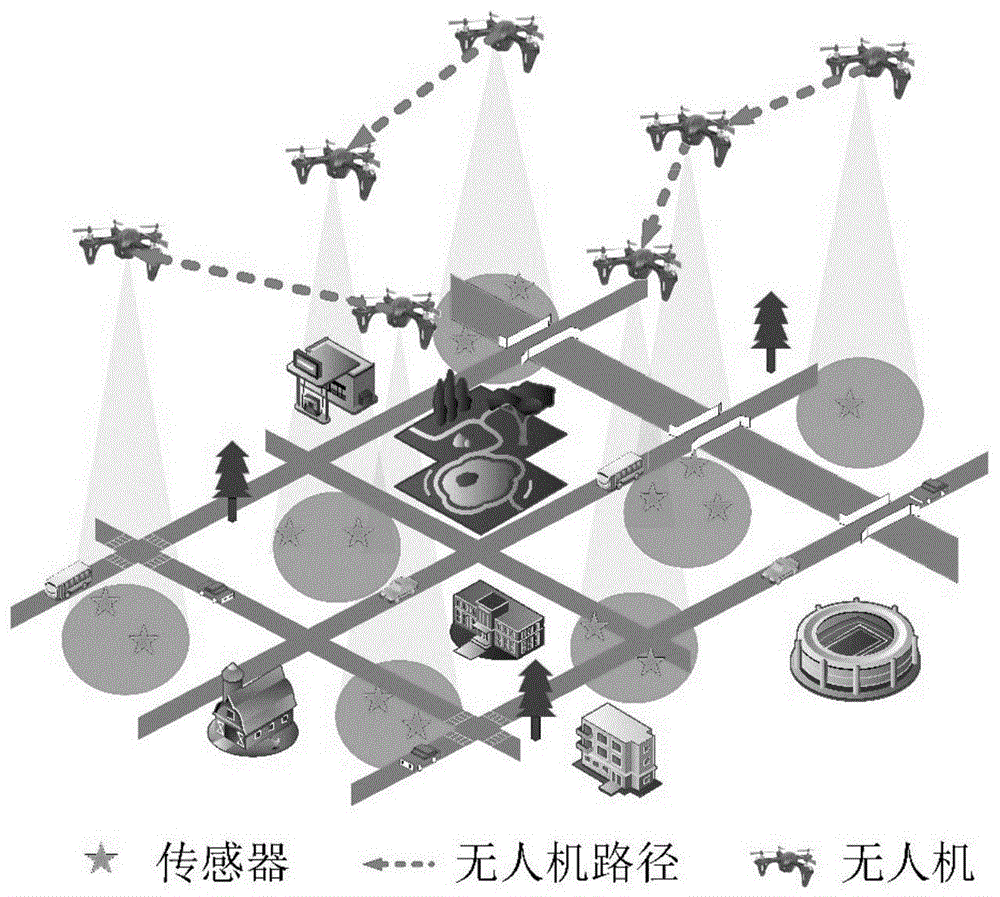
图1为面向多无人机的信息采集场景示意图。
图2为本发明的流程图。
图3为无人机悬停点设计仿真结果图。
图4为多无人机最大任务完成时间与传感器个数关系仿真结果图。
图5为多无人机最大任务完成时间与无人机个数关系仿真结果图。
图6为多无人机最大任务完成时间与通信半径关系仿真结果图。
图7为多无人机最大任务完成时间与监测区域范围关系仿真结果图。
具体实施方式
如图2所示,一种基于任务完成时间最小化的多无人机路径规划方法,考虑有k架无人机协同对无线传感器网络中传感器的信息进行采集。在考虑信息采集质量的前提下,通过对k架无人机的路径规划,实现用时最长的无人机任务完成时间最小化的目标,具体步骤为:
步骤1、设定多无人机飞行约束条件和需要满足的信息采集任务要求,具体为:
式中,li(0)表示无人机i的初始位置,li(t)表示无人机i的最终位置,
||li(t)||是无人机i在t时刻的速度,vmax是无人机最大速度;||li(t)-li'(t)||表示无人机i与i'之间的距离,dmin表示无人机之间保证避碰的最小距离;r表示无人机投影在地面的最大通信半径,||li′(t)-cj′||表示无人机i地面投影点与传感器j之间的距离。
式(1)保证了无人机完成任务后回到起始位置;式(2)保证了无人机在每个传感器上收集的信息都满足吞吐量要求;式(3)保证了每架无人机在t时刻最多只与一个传感器通信;式(4)保证了每个传感器在t时刻最多只由一个无人机提供服务;式(5)保证了无人机的飞行速度不超过其最大速度;式(6)保证了多无人机飞行的时候避免碰撞;式(7)保证了无人机的信息采集质量。
步骤2、根据基站覆盖原理以及设定的信息采集任务要求,确定无人机在信息采集任务过程中的悬停点,在该点无人机可以依次从多个传感器中收集信息。将悬停点选择问题建模为基站覆盖问题。实现方法为:给定传感器的位置和无人机的通信半径,目标是找到最小数量的悬停点和相应位置,使得每个传感器至少被一个悬停点覆盖,具体步骤如下:
步骤2.1、将x定义为已经被覆盖的传感器集合,初始化为空集合;将y定义为未被覆盖的传感器集合,初始化为传感器集合p;将v定义为悬停点集合,初始化为空集合;
步骤2.2、利用凸包的计算方法计算y集合中边界传感器,将其存在ybo集合中,y集合中剩余传感器存在yin集合中;
步骤2.3、随机选择ybo集合中一个传感器b0,并且将ybo集合中与b0的距离在2r范围内的传感器存在集合ρ中,r是无人机在地面上的最大通信半径;
步骤2.4、利用选址问题中寻找中心位置的算法,找到可以覆盖ρ中所有传感器的悬停位置hm,并计算ρ中所有传感器与hm的距离,记录下最大距离d;
步骤2.5、比较d与r的大小关系,若d>r,删除ρ中距离hm最远的点;
步骤2.6、重复步骤2.4-2.5,直到d≤r;
步骤2.7、将yin集合中与hm的距离在r范围以内的传感器存入ρ集合,距离在[r,2r]范围内的传感器存入θ集合中;
步骤2.8、在θ中找到距离hm最近的点b′,把b′从θ中删除,并将其添加到ρ集合中,重复步骤2.4,得到悬停位置hm和最大距离d。
步骤2.9、判断最大距离d与通信半径r的关系。如果d≤r,返回步骤2.8,直到θ集合为空集合;如果d≥r,将b′从ρ中删除,执行步骤2.10;
步骤2.10、更新x,y,v集合,其中x=x∪ρ,y=y/ρ,v=v∪hm;
步骤2.11、重复步骤2.2-2.10,直到所有传感器被覆盖,即y集合为空集合。
步骤3、根据设计的悬停点和飞行约束条件,利用最小-最大路径覆盖算法,规划每架无人机的路径,完成信息采集任务的分配。
根据悬停点位置,利用最小-最大路径覆盖算法,将信息采集任务进行分配并规划每架无人机的路径。先利用旅行商问题的算法计算一条覆盖所有悬停点的无人机路径,然后计算各个任务所需要的飞行时间和悬停时间,根据无人机任务用时公平性原则进行任务分配和路径分解,最终得到每架无人机的任务分配和其路径,具体步骤为:
步骤3.1、利用旅行商问题的算法计算一条覆盖所有悬停点的无人机路径;
步骤3.2、只考虑悬停时收集信息的情形,计算无人机在悬停点vm执行信息采集任务需要的悬停时间h(vm)、在悬停点之间飞行所需要的飞行时间w(vm,vm+1)以及总时间w(c);
步骤3.3、计算路径分解向量b=(b1,...,bi,...,bk),其中
步骤3.4、根据步骤3.1得到的路径,建立悬停点和路径的组合序列ve=(ve0=v0,ve1=e(v0,v1),ve2=v1,ve3=e(v1,v2),...,ve2n+1=v0),其中vm表示悬停点,e(vm,vm+1)表示悬停点vm和vm+1之间的路径;
步骤3.5、悬停点和路径的子序列(veo,ve1,...,vej(i))的总权重为wh(veo,ve1,ve2,ve3,...,vej(i))=h(ve0)+w(ve1)+h(ve2)+w(ve3)+....+h(vej(i))/w(vej(i)),其中h(ve2m)为悬停时间,w(ve2m+1)为飞行时间。
步骤3.6、根据判定条件wh(veo,ve1,...,vej(i))≤bi,在ve序列中寻找路径分界点vej(i),1≤i≤k;
步骤3.7、如果路径分界点vej(i)是边,则将该边删除,vej(i)=vej(i)-1作为无人机i初始路径的终点,ve′j(i)=vej(i)+1作为无人机i+1初始路径的起点;
步骤3.8、如果路径分界点vej(i)是点,则vej(i)=vej(i)-2作为无人机i初始路径的终点,ve′j(i)=vej(i)作为无人机i+1初始路径的起始点;
步骤3.9、重复步骤3.6~3.8,直到i=k,得到k架无人机的初始路径c={c1,...,ci,...,ck},其中ci为无人机i的初始路径,即ci=(ve′j(i-1),...,vej(i));
步骤3.10、将初始路径加上无人机从起点飞行到任务区域的路径,构成k架无人机的闭合路径。
步骤4、基于规划的无人机路径,对飞行时间和信息采集时间进行优化分配,得到最终的无人机轨迹。
在步骤4中,基于步骤3中规划的无人机路径,进一步考虑无人机在飞行时采集信息的情形,对飞行时间和信息采集时间进行优化分配,具体方法为:
式中,
式(12)保证了无人机新的悬停时间不超过优化前的悬停时间;式(12)保证了无人机在某段路程中飞行时的信息采集时间
实施例
一种基于任务完成时间最小化的多无人机路径规划方法,具体应用如下:
如图1所示,考虑用多架无人机对5km×5km的区域内n个传感器进行信息采集。无人机飞行高度为50m,无人机间避碰的最小距离为100m,投影在地面的通信半径为500m。信息传输功率为10dbm,总带宽为1mhz,高斯白噪声功率为-110dbm,每米信道功率增益为50dbm。本实施例对比了四种不同的路径规划方法:1)每架无人机负责的传感器数量相同。首先计算一条覆盖所有传感器的路径,然后根据任务数相等的原理对路径进行分解;2)利用多旅行商问题的算法得到每架无人机的轨迹;3)利用k-均值算法计算悬停点位置,然后利用最小-最大路径覆盖算法得到每架无人机的轨迹。
本实施例对比了四种不同的路径规划方法:1)任务平均算法:首先进行信息采集任务分配,将信息采集任务平均分配给每架无人机。然后每架无人机根据各自分配的任务,利用旅行商算法规划路径;2)多旅行商算法:直接利用多旅行商问题的算法得到每架无人机的轨迹;3)k-均值算法:首先利用k-均值聚类算法计算悬停点位置,然后根据悬停点位置和信息采集任务要求,利用最小-最大路径覆盖算法得到每架无人机的轨迹。
图3表示在5km×5km的监测区域内对70个传感器的悬停点设计的仿真结果图。图4表示在无人机个数为3时,传感器个数由10增长至120的过程中,多无人机中最大任务完成时间的变化趋势;图5表示在传感器个数为100时,无人机个数由1增长至10的过程中,多无人机中最大任务完成时间的变化趋势;图6表示在传感器个数为120且无人机个数为3时,通信半径由100m增长至800m的过程中,多无人机中最大任务完成时间的变化趋势;图7表示在传感器个数为100且无人机个数为3时,监测区域由1km×1km扩大至9km×9km的过程中,多无人机中最大任务完成时间的变化趋势;
如图3所示,利用20个悬停点就可以将70个传感器全部覆盖,可以有效地减少无人机在传感器之间飞行的时间,降低任务完成时间。
如图4所示,随着传感器个数的增多,采用本发明设计的方案来对度无人机路径进行规划,多无人机的最大任务完成时间小于其它三种方案。
如图5所示,随着无人机个数的增多,本发明设计的方案中多无人机中最大任务完成时间小于另外三种方案,且由图可得,无人机个数小于等于4时,任务完成时间下降较快,当无人机组数大于4时,下降迟缓,因此从经济角度,无人机个数可根据实验结果选择合适的值,达到经济高效的效果。
如图6所示,随着通信半径的变化,本发明设计的方案的任务完成时间是四个方案中最小的,且随通信半径的增加而下降。
如图7所示,在不同大小的监测场景中,本发明在降低任务完成时间方面明显优于其他算法。
- 还没有人留言评论。精彩留言会获得点赞!