未知视距和非视距分布情况下基于到达时间的定位方法与流程

本发明涉及一种目标定位方法，尤其是涉及一种未知视距和非视距分布情况下基于到达时间的定位方法。

背景技术：

近年来，无线传感器网络中的目标定位技术在导航、通信和目标跟踪等领域中已得到了广泛应用。随着技术的发展与社会的进步，高精度的目标定位技术在各个领域展现出了广泛的应用前景。因此，对无线传感器网络中高精度的目标定位方法的研究十分有必要。

根据接收信号的特征参数和应用环境的不同，人们提出了各种目标定位方法，分别有到达时间(toa)、到达时间差(tdoa)、到达角度(aoa)、接收信号强度(rss)以及各种定位技术的混合定位等方法。这些传统的目标定位方法一般是假设信号源与传感器之间的传播是视距(los)传播，且视距链路分布已知，然而在复杂的城市或室内等恶劣的环境中常存在障碍物的阻碍，直接使用这些目标定位方法会导致定位精度非常低。因此，需要寻找一种适用于混合视距(los)和非视距(nlos)环境的高性能目标定位方法。

目前，很多适用于混合视距和非视距环境的目标定位方法都需要知道视距链路和非视距链路的分布情况。chanyt在已知视距链路和非视距链路的分布情况下抛弃了非视距链路的信息，用视距定位的方法对其它链路进行定位，但是该方法需要保证视距链路至少有3条。为了解决视距链路较少时的定位问题，venkateshs提出了一种线性规划方法，其将视距链路的信息用于构建目标函数，而非视距链路的信息用于构建约束条件。上述方法都需要知道视距链路和非视距链路的分布情况，然而这在实际中很难准确获取。

因此，研究一种不需要知道视距链路和非视距链路分布情况的目标定位方法是十分有必要的。

技术实现要素：

本发明所要解决的技术问题是提供一种未知视距和非视距分布情况下基于到达时间的定位方法，其无需知道视距链路和非视距链路的分布情况，且定位精度高。

本发明解决上述技术问题所采用的技术方案为：一种未知视距和非视距分布情况下基于到达时间的定位方法，其特征在于包括以下步骤：

步骤一：设定无线传感器网络中存在一个未知的目标节点和n个已知的锚节点，并设定无线传感器网络中的视距和非视距链路的分布情况未知；为无线传感器网络建立一个平面坐标系作为参考坐标系，将目标节点在参考坐标系中的坐标位置记为x，将第i个锚节点在参考坐标系中的坐标位置记为si；其中，n为正整数，n≥3，i为正整数，i的初始值为1，1≤i≤n；

步骤二：建立目标节点与每个锚节点之间的距离测量模型，如果目标节点与第i个锚节点之间为视距传播，则将目标节点与第i个锚节点之间的距离测量模型描述为：di＝||x-si||+ni；如果目标节点与第i个锚节点之间为非视距传播，则将目标节点与第i个锚节点之间的距离测量模型描述为：di＝||x-si||+bi+ni；然后将无线传感器网络中的所有视距链路视为非视距链路，针对第i个锚节点，目标节点与第i个锚节点之间的距离测量模型选用di＝||x-si||+bi+ni；其中，di表示目标节点与第i个锚节点之间的距离测量值，符号“||||”为范数符号，||x-si||表示目标节点与第i个锚节点之间的真实距离，ni表示服从均值为0且方差为σi²的高斯分布的测量噪声，bi表示目标节点与第i个锚节点之间的非视距链路中的非视距偏差，bi在[0,ρ]范围内服从均匀分布，ρ表示无线传感器网络中的非视距链路中的非视距误差最大值，bi＞＞ni，bi≤ρ；

步骤三：对等式di＝||x-si||+bi+ni两边进行平方，得到然后将中的高阶项舍去，整理后得到ni的近似表达式为再根据并采用最坏情况下的鲁棒最小二乘方法，得到ni的最小化问题，描述为：其中，min()为最小值函数，max()为最大值函数，1≤i≤n；

步骤四：令f(bi)在[0,ρ]范围内单调递减；然后将转化为接着将转化为max(|f(0)|,|f(ρ)|)，进而将转化为目标函数，描述为：其中，f(bi)为引入的中间变量，符号“||”为取绝对值符号，f(0)表示取bi＝0时f(bi)的值，f(ρ)表示取bi＝ρ时f(bi)的值，

步骤五：在目标函数中引入辅助变量t，将目标函数转化为然后在中引入辅助变量h和r，并令h中的第i个元素hi＝||x-si||²，r中的第i个元素ri＝||x-si||，将转化为非凸问题，描述为：接着利用凸松弛技术对非凸问题中的约束条件hi＝||x-si||²进行松弛，对应得到其中进而将非凸问题转化为其中，ti表示t中的第i个元素，“s.t.”表示“受约束于……”，为的转置，i2表示维数为2×2的单位矩阵，z为常数变量；

步骤六：根据di＝||x-si||+bi+ni、bi＞＞ni，且bi为正，得到然后根据hi＝||x-si||²和得到再在中引入惩罚项u，u中的第i个元素ui≥0，得到进而得到凸优化问题，描述为：

步骤七：对凸优化问题进行求解，得到x的值。

所述的步骤七中，使用cvx工具箱对凸优化问题进行求解。

与现有技术相比，本发明的优点在于：

1)本发明方法将无线传感器网络中的所有视距链路视为非视距链路进行处理，不需要知道视距链路和非视距链路的具体分布情况，只需要知道非视距链路中的非视距误差最大值。

2)本发明方法根据非视距环境中的距离测量模型，采用最坏情况下的鲁棒最小二乘方法建立一个最小化的定位问题，并将这个非凸的定位问题转化为凸的定位问题即凸优化问题，而凸的定位问题易于求解。

3)本发明方法的凸优化问题中引入有惩罚项，使得目标函数更逼近非凸原定位问题，提高了目标定位精度。

附图说明

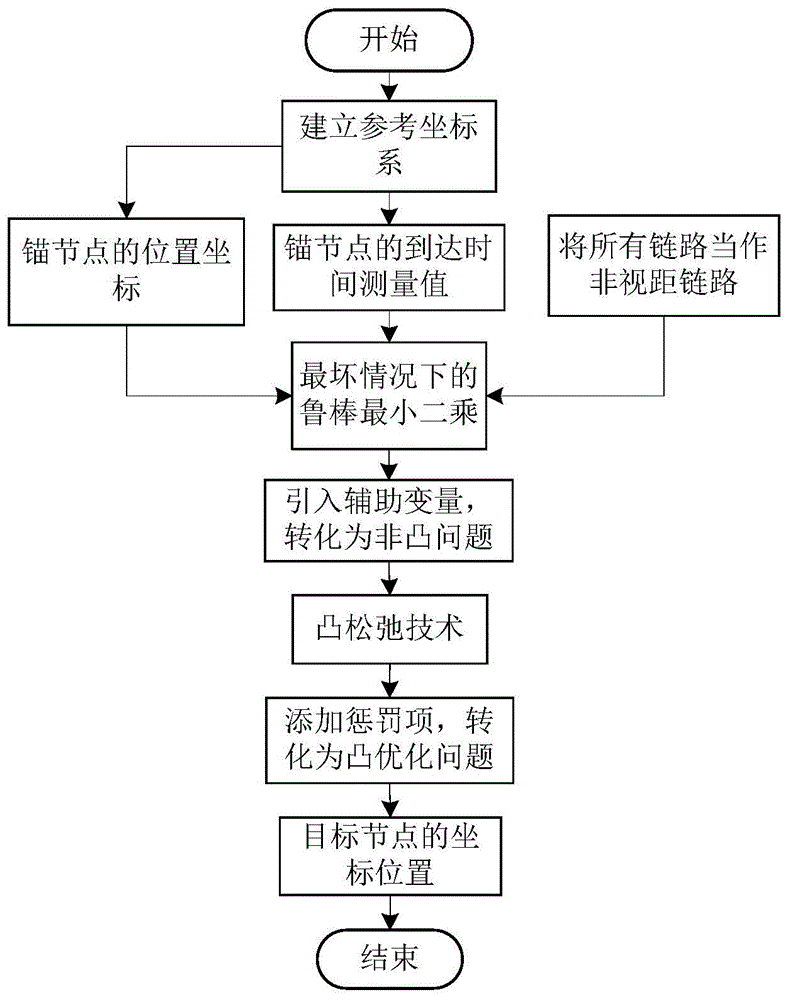
图1为本发明方法的总体实现框图；

图2为在非视距链路有4条的情况下，本发明方法、现有的鲁棒加权最小二乘(r-wls)方法、现有的鲁棒二阶锥(r-socp)方法的rmse随噪声标准差的变化曲线；

图3为在噪声标准差为0.6米的情况下，本发明方法、现有的鲁棒加权最小二乘(r-wls)方法、现有的鲁棒二阶锥(r-socp)方法的rmse随非视距(nlos)链路数量的变化曲线；

图4为在非视距链路有4条且噪声标准差为0.6米的情况下，本发明方法、现有的鲁棒加权最小二乘(r-wls)方法、现有的鲁棒二阶锥(r-socp)方法的累计分布函数(cdf)随估计误差的变化曲线。

具体实施方式

以下结合附图实施例对本发明作进一步详细描述。

本发明提出的一种未知视距和非视距分布情况下基于到达时间的定位方法，其总体实现框图如图1所示，其包括以下步骤：

步骤一：设定无线传感器网络中存在一个未知的目标节点和n个已知的锚节点，并设定无线传感器网络中的视距和非视距链路的分布情况未知；为无线传感器网络建立一个平面坐标系作为参考坐标系，将目标节点在参考坐标系中的坐标位置记为x，将第i个锚节点在参考坐标系中的坐标位置记为si；其中，n为正整数，n≥3，在本实施例中取n＝8，i为正整数，i的初始值为1，1≤i≤n。

步骤二：建立目标节点与每个锚节点之间的距离测量模型，如果目标节点与第i个锚节点之间为视距传播，则将目标节点与第i个锚节点之间的距离测量模型描述为：di＝||x-si||+ni；如果目标节点与第i个锚节点之间为非视距传播，则将目标节点与第i个锚节点之间的距离测量模型描述为：di＝||x-si||+bi+ni；由于不知道视距链路和非视距链路的分布情况，因此然后将无线传感器网络中的所有视距链路视为非视距链路，针对第i个锚节点，目标节点与第i个锚节点之间的距离测量模型选用di＝||x-si||+bi+ni；其中，di表示目标节点与第i个锚节点之间的距离测量值，di已知，符号“||||”为范数符号，||x-si||表示目标节点与第i个锚节点之间的真实距离，ni表示服从均值为0且方差为σi²的高斯分布的测量噪声，bi表示目标节点与第i个锚节点之间的非视距链路中的非视距偏差，bi在[0,ρ]范围内服从均匀分布，ρ表示无线传感器网络中的非视距链路中的非视距误差最大值，ρ一般根据具体的无线传感器网络进行设定，如将ρ设定为5米，bi＞＞ni，bi≤ρ。

步骤三：对等式di＝||x-si||+bi+ni两边进行平方，得到由于高阶项比较小，因此然后将中的高阶项舍去，整理后得到ni的近似表达式为再根据并采用最坏情况下的鲁棒最小二乘方法，得到ni的最小化问题，描述为：其中，min()为最小值函数，max()为最大值函数，1≤i≤n。

步骤四：令f(bi)在[0,ρ]范围内单调递减；然后将转化为由于f(bi)在[0,ρ]范围内单调递减，因此接着将转化为max(|f(0)|,|f(ρ)|)，进而将转化为目标函数，描述为：其中，f(bi)为引入的中间变量，符号“||”为取绝对值符号，f(0)表示取bi＝0时f(bi)的值，f(ρ)表示取bi＝ρ时f(bi)的值，

步骤五：为了将目标函数变为标准形式，在目标函数中引入辅助变量t，将目标函数转化为然后在中引入辅助变量h和r，并令h中的第i个元素hi＝||x-si||²，r中的第i个元素ri＝||x-si||，将转化为非凸问题，描述为：接着利用凸松弛技术对非凸问题中的约束条件hi＝||x-si||²进行松弛，对应得到其中进而将非凸问题转化为其中，ti表示t中的第i个元素，“s.t.”表示“受约束于……”，为的转置，i2表示维数为2×2的单位矩阵，z为常数变量。

步骤六：根据di＝||x-si||+bi+ni、bi＞＞ni，且bi为正，得到然后根据hi＝||x-si||²和得到由于在视距链路ni＜0时不成立，因此再在中引入惩罚项u，u中的第i个元素ui≥0，得到进而得到凸优化问题，描述为：

步骤七：使用cvx工具箱对凸优化问题进行求解，得到x的值。

为了验证本发明方法的可行性和有效性，通过蒙特卡洛仿真实验来比较本发明方法和其它定位算法的性能。

当目标节点与第i个锚节点之间为视距传播时，目标节点与第i个锚节点之间的距离测量模型为di＝||x-si||+ni；当目标节点与第i个锚节点之间为非视距传播时，目标节点与第i个锚节点之间的距离测量模型为di＝||x-si||+bi+ni，利用di＝||x-si||+ni和di＝||x-si||+bi+ni用于生成测量距离。假设锚节点和目标节点随机分布于20米×20米正方形区域内。锚节点数量n＝8，锚节点和目标节点的测量噪声为ni，无线传感器网络中的非视距链路中的非视距误差最大值ρ设定为5米。在此以均方根误差(rmse)来评估定位方法的性能，其定义为：其中，mc表示蒙特卡洛运行次数，mc＝10000，k的初始值为1，1≤k≤mc，表示第k次蒙特卡洛仿真中目标节点在参考坐标系中的估计位置，xk表示第k次蒙特卡洛仿真中目标节点在参考坐标系中的真实位置。

图2给出了在非视距链路有4条的情况下，本发明方法、现有的鲁棒加权最小二乘(r-wls)方法、现有的鲁棒二阶锥(r-socp)方法的rmse随噪声标准差的变化曲线。从图2中可以看出，所有定位方法中，rmse都随着噪声标准差的增大而增大，而本发明方法在噪声标准差较小时性能明显更好。

图3给出了在噪声标准差为0.6米的情况下，本发明方法、现有的鲁棒加权最小二乘(r-wls)方法、现有的鲁棒二阶锥(r-socp)方法的rmse随非视距(nlos)链路数量的变化曲线。从图3中可以看出，随着非视距链路数量的增多，本发明方法和鲁棒二阶锥(r-socp)方法的rmse随之增大，而鲁棒加权最小二乘(r-wls)方法的rmse随之减小；在非视距链路数量较少时，本发明方法的定位性能明显较好。

图4给出了在非视距链路有4条且噪声标准差为0.6米的情况下，本发明方法、现有的鲁棒加权最小二乘(r-wls)方法、现有的鲁棒二阶锥(r-socp)方法的累计分布函数(cdf)随估计误差的变化曲线。从图4中可以看出，在累计分布函数到达90％时，鲁棒加权最小二乘(r-wls)方法的估计误差为6.52米、鲁棒二阶锥(r-socp)方法的估计误差为13.79米，而本发明方法的估计误差为5.74米，可以看出，在相同条件下，本发明方法的定位性能更好。