一种基于振动信号去噪和包络分析的滚动轴承故障诊断方法与流程

本发明涉及一种基于振动信号去噪和包络分析的滚动轴承故障诊断方法，属于机械故障诊断及信号处理领域。
背景技术：
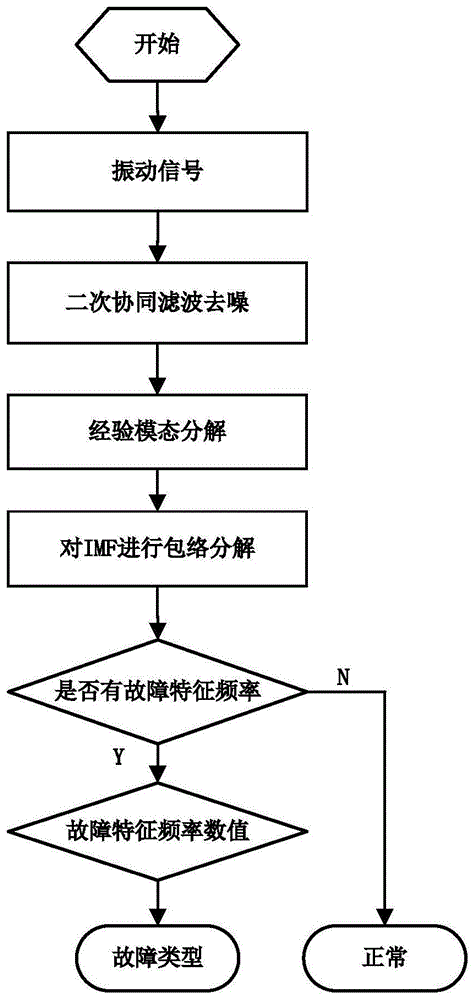
：滚动轴承是旋转设备及其他机械设备的最主要零部件之一，它的性能对整个设备的运行起决定性的作用。但是滚动轴承恶劣的工作环境使它出现故障的可能性很大，所以对滚动轴承的运行状态进行诊断以便及时采取措施对设备的正常运行非常重要。因此滚动轴承的诊断技术的研究具有重要的意义。因为振动信号包含了大部分的设备运转时的状态信息，并且振动信号容易采集，所以对振动信号的分析是最有用的故障诊断方向之一。当滚动轴承出现缺陷时，轴承共振高频会因为受到内圈，外圈，滚动体产生的脉冲激励从而出现故障特征频率(cdf)，所以若能分离并找出cdf及其倍频就可判定滚动轴承运行状态和故障类型。但是由于滚动轴承本身的特点，安装误差，运行故障和一些外部因素对轴承运动和受力的作用使轴承以一定速度运转时会产生综合振动，振动信号中包含高斯噪声和脉冲噪声等噪声。由于噪声通常较大，轻微的轴承故障信息容易淹没于噪声中，并很难被提取分离，所以这些噪声会对分离并识别cdf产生很大的干扰，即影响故障诊断。因此本文提出了一种二次协同滤波去噪方法对振动信号进行去噪，然后再利用基于经验模态分解的包络分析方法对cdf分离进行故障诊断的方法，本方法能有效的去除噪声并分离cdf，对滚动轴承进行迅速准确的故障诊断。技术实现要素：本发明解决的技术问题是：本发明提供了一种二次协同滤波去噪方法去除振动信号中的噪声，然后对去噪后的振动信号用基于经验模态分解的包络分析方法进行故障诊断。有效的解决了振动信号中噪声的影响导致故障诊断困难的问题。本发明的技术方案是：一种基于振动信号去噪和包络分析的滚动轴承故障诊断方法，其特征在于包括如下步骤：step1：通过实验分别获取滚动轴承的外圈故障，内圈故障，滚动体故障及正常情况四种类型的振动信号。step2：对搜集到的振动信号进行二次协同滤波去噪处理，由于滚动轴承自身的特点，装配误差，运行故障等因素搜集到的振动信号包含高斯噪声和脉冲噪声等，所以对搜集的振动信号进行一次协同滤波去噪后再进行一次协同滤波处理去除干扰故障诊断的噪声。step2.1：相似块分组：设置搜索窗长为l，在搜索窗内以参考块r为中心搜索与其距离最小的m个块构成分组group(r)。设任意块为s，s与r的相似度用二者的归一化距离来度量，表达式为：其中符号||·||2表示求2范数；ω为块宽；d表示相似块之间的距离，该距离越小则s块与r的相似度越高。将group(r)以m×ω的二维数组形式保存，即group(r)∈rm×ω。以步长δ将参考块s从观测信号的始端向末端移动，搜索窗也随之移动，对在每个位置获得的相似组进行记录，并将分组中每个块的位置进行标记。step2.2：协同滤波：首先将分组group(r)进行二维离散余弦变换，表达式为：g(r)＝t{group(r)}，其中g＝[gi,j]∈rm×ω(i＝1,…,m；j＝1,…,ω)为变换系数矩阵。然后对二维离散余弦变换后的系数矩阵进行阈值处理，将小于或等于阈值的系数置零而将大于阈值的系数保留，阈值的定义为：最后通过逆变换获得滤波后的分组。step2.3：聚合重构：由于相似块之间存在重叠，一个信号通常会同时属于多个相似块，信号点的重构通过聚合所有包含的相似块在该位置的滤波输出实现，聚合方式采用算术平均，表达式为：其中xs,r(n)为分组group(r)中相似块s在信号点n的滤波输出，fs(n)的表达式为：step3：对去除噪声后的振动信号进行经验模态分解，经验模态分解后的振动信号被分解成若干个内蕴模态函数(imf)。step3.1：获取振动信号x(t)的所有极大值和极小值点，用三次样条函数对极值点进行拟合，分别形成上下包络曲线。step3.2：求得上下包络曲线的均值m1，用待分解的振动信号x(t)减去均值m1得到h1，判断h1是否满足成为imf的两个条件。如果满足则把h1看作是imf分量，记作c1(t)，残差量r1＝x(t)-c1(t)看作是待分解信号；如果不满足则把h1看作是待分解信号x(t)。重复step3.1和step3.2，重复k次直到满足imf的条件为止。step3.3：把残差量当作待分解信号，令x(t)＝r，重复步骤step3.1和step3.2继续筛选，直至残差量为一个单调函数不能再分解为止，表达式如下：最终x(t)经过经验模态分解为：step4：选取imf1进行包络分析，从包络谱中寻找有无特征频率及其倍频，若有则根据频率的大小判断故障类型，若没有则是正常状态。step4.1：把经过经验模态分解得到的imf进行希尔伯特变换:step4.2：h[ci(t)]和ci(t)组成分析信号：其中step4.3：对yj(t)进行傅里叶变换获得包络谱。本发明用二次协同滤波方法对振动信号进行去噪，协同滤波方法利用振动信号中的具有相似块的特点和二维线性变换的优点对振动信号中的噪声进行有效的去除，与传统的小波变换和非局部均值去噪相比本发明提出的去噪方法具有更优越的去噪性能，能达到更好的去噪效果，能更加有利于故障诊断。本发明使用基于经验模态分解的包络分析方法进行故障诊断，故障特征频率主要在高频，而经验模态分解可以把信号分解成从高频到低频的imf，对高频imf进行包络分析从而分离出故障特征频率，与传统的傅里叶变换相比，本方法能更加有效的分离故障特征频率，因此更有利于故障诊断。附图说明图1为本发明的流程图。图2为二次协同滤波去噪流程图。图3为正常情况，内圈故障，外圈故障的振动信号时域图。图4为内圈故障振动信号经过二次协同滤波后再进行基于经验模态分解的包络分析的包络谱。图5为外圈故障振动信号经过二次协同滤波后再进行基于经验模态分解的包络分析的包络谱。图6为内圈故障振动信号经过非局部均值去噪后再进行基于经验模态分解的包络分析的包络谱。图7为外圈故障振动信号经过非局部均值去噪后再进行基于经验模态分解的包络分析的包络谱。图8为内圈故障振动信号经过小波去噪后再进行基于经验模态分解的包络分析的包络谱。图9为外圈故障诊断信号经过小波去噪后再进行基于经验模态分解的包络分析的包络谱。图10为内圈故障直接进行傅里叶变换的频谱图。图11为外圈故障直接进行傅里叶变换的频谱图。具体实施方式下面结合附图对本发明的具体实施方式进行描述，以便本领域的技术人员更好的理解本发明。但是本发明不限于具体实施方式的范围。此外应理解，在阅读了本发明的内容之后，本领域技术人员可以对本发明作各种改动或修改，这些等价形式同样落于本申请所附权力要求书所限定的范围。图1是本发明的流程图，本发明包括以下步骤：step1：通过实验分别获取滚动轴承的外圈故障，内圈故障及正常情况三种种类型的振动信号。本发明以美国西储大学轴承数据中心的滚动轴承故障诊断为例，该滚动轴承故障诊断实验装置由一个扭矩仪，一个功率计，一个三相感应电动机等组成，电动机驱动端转子由测试轴承(即诊断对象)支撑，并在测试轴承中通过放电加工设置了单点故障，故障直径包括7mils、14mils、21mils和28mils(即故障严重程度)，故障类型包括内圈故障，滚动体故障，外圈故障。电动机驱动端罩壳上安装有一个带宽高达5000hz的加速计，并通过一个记录仪采集测试轴承在不同工作状态下的振动数据。实验中所用的深沟滚动轴承型号为6205-2rsjemskf，其参数如表1所示。本次具体实施方式采用的数据采样频率为4800hz，故障直径为7mil，3点钟方向故障状态的内圈故障和外圈故障为例，其时域图如图3所示。表1滚动轴承参数球的数量接触角球的直径中径内环直径外环直径厚度900.31621.5370.98432.04720.5906step2：对搜集到的振动信号进行二次协同滤波去噪处理，由于滚动轴承自身的特点，装配误差，运行故障等因素搜集到的振动信号包含高斯噪声和脉冲噪声等，所以对搜集的振动信号进行一次协同滤波去噪后再进行一次协同滤波处理去除干扰故障诊断的噪声。流程图如图2所示，协同滤波去噪分为三个步骤:相似块分组，协同滤波和聚合重构。具体过程如下：step2.1：相似块分组：设置搜索窗长为l，在搜索窗内以参考块r为中心搜索与其距离最小的m个块构成分组group(r)。设任意块为s，s与r的相似度用二者的归一化距离来度量，表达式为：其中符号||·||2表示求2范数；ω为块宽；d表示相似块之间的距离，该距离越小则s块与r的相似度越高。将group(r)以m×ω的二维数组形式保存，即group(r)∈rm×ω。以步长δ将参考块s从观测信号的始端向末端移动，搜索窗也随之移动，对在每个位置获得的相似组进行记录，并将分组中每个块的位置进行标记。其中参数搜索窗长度l为4000，块宽ω为30，步长δ为1。step2.2：协同滤波：首先将分组group(r)进行二维离散余弦变换，表达式为：g(r)＝t{group(r)}，其中g＝[gi,j]∈rm×ω(i＝1,…,m；j＝1,…,ω)为变换系数矩阵。然后对二维离散余弦变换后的系数矩阵进行阈值处理，将小于或等于阈值的系数置零而将大于阈值的系数保留，阈值的定义为：最后通过逆变换获得滤波后的分组。step2.3：聚合重构：由于相似块之间存在重叠，一个信号通常会同时属于多个相似块，信号点的重构通过聚合所有包含的相似块在该位置的滤波输出实现，聚合方式采用算术平均，表达式为：其中xs,r(n)为分组group(r)中相似块s在信号点n的滤波输出。step3：对去除噪声后的振动信号进行经验模态分解，经验模态分解后的振动信号被分解成若干个内蕴模态函数(imf)。step3.1：获取振动信号x(t)的所有极大值和极小值点，用三次样条函数对极值点进行拟合，分别形成上下包络曲线。step3.2：求得上下包络曲线的均值m1，用待分解的振动信号x(t)减去均值m1得到h1，判断h1是否满足成为imf的两个条件。如果满足则把h1看作是imf分量，记作c1(t)，残差量r1＝x(t)-c1(t)看作是待分解信号；如果不满足则把h1看作是待分解信号x(t)。重复step3.1和step3.2，重复k次直到满足imf的条件为止。step3.3：把残差量当作待分解信号，令x(t)＝r，重复步骤step3.1和step3.2继续筛选，直至残差量为一个单调函数不能再分解为止，最终x(t)经过经验模态分解为：step4：选取imf1进行包络分析，从包络谱中寻找有无特征频率及其倍频，若有则根据频率的大小判断故障类型，若没有则是正常状态。step4.1：把经过经验模态分解得到的imf进行希尔伯特变换:step4.2：h[ci(t)]和ci(t)组成分析信号：其中step4.3：对yj(t)进行傅里叶变换获得包络谱。内圈故障和外圈故障包络谱如图4和图5所示。内圈故障和外圈故障特征频率计算公式为：内圈故障特征频率fa：外圈故障特征频率fo：内圈故障和外圈故障的故障特征频率如表2所示。表2故障特征频率内圈故障外圈故障162.2hz107.4hz为了证明本发明的有效性和优势，本发明选择了传统的非局部均值去噪和小波去噪方法与本发明的方法进行对比，这两种方法的代码来自于网上公开的matlab代码。图6和图7是非局部均值去噪后的内圈故障和外圈故障包络谱，图8和图9是小波去噪后的内圈故障和外圈故障包络谱。图10和图11是直接傅里叶变换的频谱图。从图4，图5和图6，图7，图8，图9的对比可以明显看出经过二次协同滤波去噪后的包络谱受噪声影响小，故障特频率幅值相比较于噪声频率幅值更大，更容易识别从而能快速的进行故障诊断；并且有更多的倍频可以识别从而提高了故障诊断的准确性。通过与图10，图11的对比可以看出直接进行傅里叶变换不能分离出故障特征频率，而通过基于经验模态分解的包络分解能分离出故障特征频率及其倍频，有利于故障诊断。综上，本发明提出的二次协同滤波去噪方法能够有效的去除振动信号中的噪声，基于经验模态分解的包络分析能有效分离故障特征频率进而有效快速的进行故障诊断。当前第1页12