基于信号稀疏表示的NPC三电平逆变器故障诊断方法与流程

本发明属于电力电子故障诊断领域。
背景技术：
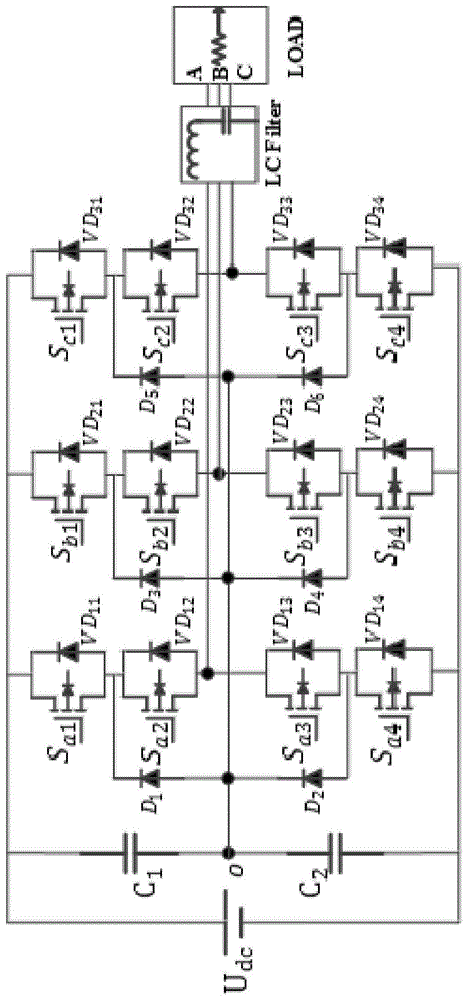
：近年来，在高压大功率应用场合，三电平逆变器受到越来越多的关注，它产生的背景是为了克服传统两电平逆变器开关应力大，直流母线电压利用率低等缺点，通过对主电路拓扑的改进，使得三电平逆变器具有相当多的优势，例如功率器件串联均压、功率管应力低，电磁干扰问题小，输出电压电流的谐波含量低，工作效率高等。虽然三电平逆变器有诸多优点，但是由于电平数增加，主电路中功率管数量成倍的增加，电路结构和内部的控制策略变得更加复杂，并且功率管在驱动信号的作用下始终要高频率的进行的导通和截止状态的切换，同时还要承受高电压和大电流，基于以上种种因素，三电平逆变器发生故障的可能性变大，导致逆变系统的可靠性降低。三电平逆变器的故障主要与功率管故障有关，逆变器在工作过程中功率管会发生短路故障和开路故障。通常，逆变装置中会设计保护电路，功率管一旦发生短路故障，保护电路迅速作用，将短路故障转为开路故障，以开路故障的形式进行诊断。虽然人们为了提高系统的可靠性和可维护性而采取降额设计或者采用并联冗余器件或电路的方法，但这些方法会使系统的造价提高，同时在一些体积和重量严格受限的场合，冗余设计难以满足要求。为改善这种状况，已有学者提出逆变器的容错技术，即在诊断出系统故障后，通过自动补偿故障的影响来维持系统的稳定性和尽可能地恢复系统故障前的性能，但是准确的故障诊断结果是进一步实施容错控制的前提和保障。所以，对逆变器的故障诊断策略进行研究，研究有效的故障诊断方法，及时分析处理故障征兆，确定故障发生的位置就显得尤为重要。三电平逆变器至今已有多年的发展历程，产生了大量拓扑结构，其基本拓扑结构可以分为三类：h桥级联型、中点箝位型(npc)和飞跨电容型。由于中点箝位型多电平逆变器性能稳定、控制较易实现等优点，已逐渐成为多电平逆变器的主流。本发明主要针对npc三电平逆变器进行故障诊断研究。故障特征提取技术和故障辨识技术是实现逆变器故障诊断两个难点。故障特征提取是指当逆变器发生故障，对相关物理量进行分析，采用适当的特征提取技术，提取这些物理量的特征信息，使得提取到的特征信息能够完整准确的表征当前故障类型(故障特征提取是故障诊断的前提)。故障辨识是指根据故障特征提取技术提取到的故障特征信息，采用有效的故障辨识方法，实现故障的诊断和定位。技术实现要素：本发明的目的是提出一种基于信号稀疏表示的npc三电平逆变器故障诊断方法。本发明是通过以下技术方案实现的。本发明所述的一种基于信号稀疏表示的npc三电平逆变器故障诊断方法，包括如下步骤：(1)故障模型的建立：对npc三电平逆变器的拓扑结构和开路故障类型进行分析，同时在matlab/simulink环境搭建npc三电平逆变器故障仿真模型，模拟开路故障类形。采样三相相电压信号y作为分析的特征信号。(2)故障特征提取：对三相相电压信号y进行分析，通过信号稀疏表示的方法，得到过完备字典d和稀疏系数(稀疏编码)x，将稀疏系数x作为信号的特征信息。(3)故障辨识：建立多分类支持向量机模型，用训练样本对支持向量机进行训练，将已训练的支持向量机保存。用测试样本测试训练好的支持向量机模型，分析故障诊断结果。进一步地，所述的步骤(2)故障特征提取：对三相相电压信号y进行分析，通过信号稀疏表示的方法，得到过完备字典d和稀疏系数(稀疏编码)x，将稀疏系数x作为信号的特征信息。包括以下步骤：(1)建立目标函数。用信号稀疏表示方法进行故障特征提取，目标函数为：其中，y＝[y1,y1,…,yi,…,yn]∈rm×n是特征信号，d＝[d1,d2,…,dp]∈rm×p(p＞＞m)是一个过完备字典，x＝[x1,x2,…,xi,…,xn]∈rp×n是稀疏系数矩阵，s是稀疏度。信号稀疏表示用于特征提取的过程就是求解字典d和稀疏系数矩阵x的过程，其中x即为特征信号y的特征信息；(2)k-svd算法求解d和x。如附图3包括稀疏编码(求解x)和字典更新(求解d)两个交替迭代的过程。(a)稀疏编码稀疏编码过程用于求解满足方程(2)的信号稀疏系数x：字典d是固定的，目标是找到最佳的稀疏系数矩阵x来表示信号y，本发明在稀疏编码阶段采用匹配追踪算法的优化算法正交匹配追踪算法。设特征信号为yi，则yi可以分解为其中，rmyi为第m次迭代后得到的残差，r0yi＝yi，dγn为第n次迭代匹配到的第γ个原子，<rnyi,dγn>为rnyi和dγn的内积(最大值)。式(3)为匹配追踪算法的迭代过程。在式(3)的基础上，正交匹配追踪算法通过对已经参与迭代的原子利用施密特正交化方法进行正交化处理形成一组正交基，新的参与迭代的原子属于该正交基张成空间的补空间，不会是之前已经参与迭代的原子，因此字典中的任意一个原子最多参与一次迭代。与匹配追踪算法相比，正交匹配追踪算法的收敛速度更快，正交匹配追踪算法包括以下步骤：(1)初始化残差r、稀疏系数xi和原子位置索引υ：(2)选择与残差r最大相关原子：(3)更新残差和稀疏表示系数：一般的，正交匹配追踪算法进行多次迭代才能得到满足要求的稀疏系数，若稀疏度为s，则正交匹配追踪算法步骤(2)和(3)需要迭代s次。(b)字典更新字典更新是逐列更新的，每次只更新d中某一列和x中相对应的行，而字典d其他列则固定不变，待该列完成更新后，再依次更新其他的列，更新过程为：||y-dx||2＝||ek-dkgk||2＝||ek(j)-dkgk(j)||2+c(8)式(7)中，dj为字典d的第j列，gj为稀疏系数矩阵x的第j行。当更新第k个字典原子时，除去字典d中第k列和稀疏系数矩阵x的第j行，生成误差矩阵ek。对ek进行奇异值分解，ek＝uλvt，其中u和v是酉矩阵，λ是对角元素由大到小排列的对角阵。取u的第一个列向量，作为新的dk，取v的第一个列向量与λ的第一个元素的乘积作为新的gk。用新的dk取代之前的dk，这样就完成了一个原子的更新。然而，上述操作会出现一个问题，信号稀疏表示希望得到的稀疏系数xi是稀疏的，但是新的gk可能会使稀疏系数的稀疏度达不到要求。式(8)对字典更新过程做进一步处理，gk(j)是gk中非零元素组成的缩略矩阵，ek(j)是ek的缩略矩阵，由gk非零元素的位置决定ek的缩略矩阵ek(j)，对ek(j)做svd分解，ek(j)＝uλvt。取u的第一个列向量，作为新的dk，取v的第一个列向量与λ的第一个元素的乘积作为新的gk，然后将gk中元素分配到合适位置，与更新前位置一一对应。这样就完成了一个原子的更新且保证稀疏系数满足稀疏度的约束。同理，按照相同的方法依次对字典d中其他各个原子进行更新。本发明的特点及有益效果：傅里叶变换，小波变换，主成分分析等信号分析方法是故障特征提取和故障诊断常用方法。然而，却各有优缺点。在本发明中，我们初步尝试将信号稀疏表示方法引入到三电平逆变器的特征提取中，是一种新的npc三电平逆变器故障特征提取方法，其将信号稀疏表示和支持向量机结合取得了良好的诊断效果，具有诊断正确率高等优点。附图说明附图1为npc三电平逆变器拓扑结构。附图2为npc三电平逆变器故障诊断仿真图。附图3为k-svd算法流程图。附图4为“一对一组合”多分类支持向量机结构图。附图5为npc三电平逆变器故障诊断流程图。附图6为功率管开路故障时三相电压波形图。其中，(a)为正常运行时三相电压波形图，(b)为sa1在0.04s发生故障时三相电压波形图，(c)为sa2和sa3在0.04s发生故障时三相电压波形图，(d)为sa1和sb4在0.04s发生故障时三相电压波形图。附图7为k-svd算法参数对重构误差的影响图。其中，(a)为迭代次数对重构误差的影响图，(b)为字典原子数对重构误差的影响图，(c)为稀疏度k对重构误差影响图。附图8为测试样本的辨识结果图。具体实施方式下面结合附图工作原理对具体实施方式进行说明。(1)npc三电平逆变器故障诊断流程如附图5所示，在matlab/simulink环境下搭建三电平逆变器故障诊断仿真模型如附图2所示。附图6为选取的4种不同故障情形下逆变器输出端三相相电压波形图。分析相电压波形可知，不同故障类型的相电压波形具有不同的表现形式，相电压波形隐含着反映故障类型的重要的特征信息。因此，可以将三相相电压作为待分析的特征信号，采用信号稀疏表示的方法对相电压信号进行稀疏表示获取稀疏系数，提取信号特征向量；用支持向量机方法根据提取的特征信息进行故障辨识，通过故障特征提取和故障辨识两个过程共同作用，实现对逆变器功率管的故障诊断。(2)采集数据样本。考虑到温度、光照强度和负载等因素的影响，可以改变逆变器输入端直流电压和输出端负载以获取不同工况下的样本数据。采集450v45kw、450v50kw、450v55kw、500v45kw、500v50kw、500v55kw、550v45kw、550v50kw、550v55kw工况情形下的三相相电压信号ua、ub、uc作为训练样本，由于三相相电压具有在周期性，每相相电压选择一个采样周期，采样频率为500hz，采样点数为10个，三相相电压采样后组成的新的信号维数是30，将其作为分析的特征信号，数据样本总数为657个，组成30×657的数据样本矩阵。按照同样的方法进一步采集520v45kw、520v50kw、520v55kw工况情形下三相相电压数据作为测试样本，测试样本的总数为219个，组成30×219的测试样本矩阵。(3)k-svd算法参数对重构误差的影响。样本数据根据k-svd算法自适应学习得到一个字典d和在d上稀疏系数x，x可以近似重构出原始信号y，表示重构误差。对训练样本进行分析，研究迭代次数、信号的稀疏度、初始化字典的原子数目对重构误差的影响。在附图7中，(a)表示在稀疏度为4，字典原子数目为40，,迭代次数分别在1-10的情况下的重构误差，(b)表示在稀疏度为4，字典原子数目分别为35-60情况下的重构误差，(c)表示在字典数目为40，稀疏度分别为2-7情况下的重构误差。通过分析可知，迭代次数、原子数目、稀疏度等参数对信号的重构误差产生影响，重构误差与稀疏系数x有关，因此不同的参数设置得到的不同的信号稀疏系数x，信号的稀疏系数作为故障诊断提取的特征向量，自然也会对故障诊断的精确度产生影响。(4)信号稀疏表示和支持向量机结合故障诊断。k-svd算法参数设置为迭代次数设置为10、字典原子数目设置为40、稀疏度设置为4。训练样本30×657经k-svd算法处理后得到过完备字典d和稀释系数x_train。因为稀疏度设置为4，所以每个信号的稀疏表示中非零元素的个数最多为4个，表1中(6,1)0.04657、(15,1)0.42777、(30,1)0.11003、(35,1)0.09975含义为字典d中第6、15、30、35个原子被激活去对第一个信号进行线性表示，线性表示系数分别为0.04657、0.42777、0.1103、0.09975，其他原的子未被激活，线性表示系数均为0。稀疏系数表示方法以向量(矩阵)的形式呈现，向量[0,0,…,0.04657,0,…,0.42777,0,…,0.11003,0,…,0.09975,0,…,0]为第一个信号的特征向量。因为字典原子数目为40，所以第一个信号得到的稀疏系数组成的向量由40个元素组成，其中非零元素个数为4，其余36个元素全为0。按照同样的方法得到657个数据样本的特征向量作为新的样本数据。进一步用正交匹配追踪算法得到测试样本30×219在字典d上的稀疏系数x_test。从而实现对训练数据和测试数据的全部样本数据的特征提取。在故障辨识方法上，选择“一对一”多分类支持向量机分类器对故障类型进行辨识，设置合适的参数和核函数，首先用训练数据对多分类支持向量机进行训练，完成训练结束后，得到多分类支持向量机训练模型，接着用测试样本进行测试。附图8所示为测试样本的辨识结果，通过对比测试样本的实际标签和期望标签，只有1个故障类型预测失败，测试样本的故障诊断正确率达到99.54％，仿真实验表明，基于信号稀疏表示和支持向量机结合的故障诊断方法在npc三电平逆变器故障诊断领域有很好的诊断效果。(5)不同故障诊断方法对比。为了进一步证实信号的稀疏表示和支持向量机结合方法的优越性，进行了4组对比试验。分别为小波包变换-bp神经网络实验，小波包变换-pca-bp神经网络实验，信号稀疏表示-bp神经网络实验，信号稀疏表示-支持向量机实验。仿真实验过程要运用bp神经网络和多分类支持向量机等分类模型，需要明确各种分类器输入和输出量，根据对比实验要求，分类器的输入端为不同特征提取方法提取的故障特征向量，输出端对应的是故障类型。因为npc三电平逆变器的故障类型多样，用bp神经网络和支持向量机分类器进行辨识时，需要进行故障编码和加标签进行区分，bp神经网络输出端故障编码方式用12为二进制进行编码，分别对应12个功率开关器件，0表示正常，1表示发生开路故障，如00000000表示12个功率开关器件正常，000000000001表示sa1发生开路故障，001000010000表示sb1sc2发生开路故障。支持向量机输出端以标签的形式进行故障区分，1，2，…，73分别对73种故障进行区分。四组对比试验参数设置分别为：小波包变换参数设置为小波基选取db5小波，分解层数为3层，pca参数设置为累计主元贡献率η＝90％，神经网络参数设置为隐含层函数logsig，输出层函数为tansig，训练函数为trainlm，误差为0.005。k-svd算法中，稀疏度为4，字典大小为30×40，迭代次数为10。表2为不同诊断方法的参数设置，表3为不同故障诊断方法的诊断结果。通过比较不同的故障特征提取方法和故障辨识方法，我们发现信号稀疏表示和支持向量机结合的方法故障诊断的正确率最高，相较于其他方法具有更好的诊断效果。表1部分故障稀疏结果表2对比试验参数设置表3对比试验诊断结果诊断方法诊断正确率小波包+bp神经网络91.78％(201/219)小波包+pca+bp神经网络94.52％(207/219)稀疏表示+bp神经网络98.63％(216/219)稀疏表示+支持向量机99.54％(218/219)当前第1页1 2 3