基于MEMS惯性传感器的载体动态姿态估计方法与流程

本申请涉及mems传感技术领域，尤其涉及基于mems惯性传感器的载体动态姿态估计方法。

背景技术：

智能化、无人化是当今车辆行业的发展趋势，无论是无人驾驶汽车的发展还是智能化操作的工程车辆的应用，实时、精确、稳定的姿态信息是实现智能操作、无人驾驶网络的前提。mems传感器由于其体积小、质量轻、功耗低和高可靠性的特点，在当今工业界得到了广泛的应用。但是mems惯性器件同时存在以下缺点：1)陀螺仪存在漂移误差，长时间使用会存在误差积累；2)加速度计在运动状态下受线性加速度和向心加速度影响较大，单独使用求解姿态时存在较大误差，动态性能较差。并且由于现实中磁场的干扰是随机的，误差进行预消除，单独求解航向角时误差较大。所以，使用mems惯性器件求解载体的姿态角时必须使用多种传感器组成姿态测量系统，运用合理的数据融合方法对传感器的误差进行消除和补偿，得到稳定、准确的姿态。

技术实现要素：

本申请提供一种基于mems惯性传感器的载体动态姿态估计方法，能够稳定准确的得到动态载体的姿态信息。

一种基于mems惯性传感器的载体动态姿态估计方法，包括以下步骤：

获取三轴加速度计数据并通过加速度计噪声模型进行处理；

获取三轴陀螺仪数据并通过陀螺仪噪声模型进行处理；

将以上三轴陀螺仪处理后的数据和三轴加速度计数据处理后的数据通过ekf滤波器进行处理，求取姿态角，更新姿态信息。其有益效果是：由于利用mems传感器求解载体姿态时主要存在以下几种误差：1)传感器的安装误差；2)陀螺仪的漂移和线性度误差；3)加速度计和陀螺仪的零位误差；所以通过加速度计噪声模型对加速度计数据进行处理，通过陀螺仪噪声模型对陀螺仪数据进行处理，进而稳定准确地得到动态载体的姿态信息。

在一些实施方式中，ekf滤波器处理包括以下步骤：构建卡尔曼滤波器系统模型：

其中：x(k)∈rⁿ表示k时刻系统的状态矢量；z(k)∈r^m表示k时刻系统的观测矢量；f(·)为n维矢量函数，h(·)为m维矢量函数，f(·)和h(·)对其自变量都是非线性的；w(k)∈rⁿ和v(k)∈r^m是协方差分别为q(k)和r(k)的过程噪声矢量；

建立ekf滤波器方程：包括时间更新、测量更新；

其中，时间更新包括系统状态量的先验估计和预测误差协方差矩阵的先验估计；

量测更新包括系统的卡尔曼增益、系统状态量的后验估计和预测误差协方差矩阵的后验估计。

在一些实施方式中，设系统的状态向量为：

x(k)＝(abx(k)aby(k)abz(k)ωx(k)ωy(k)ωz(k)bωx(k)bωy(k)bωz(k))^t

其中，abx(k)aby(k)abz(k)表示载体坐标系中三轴加速度测量值，ωx(k)ωy(k)ωz(k)表示载体坐标系中三轴陀螺仪测量值，bωx(k)bωy(k)bωz(k)分别为绕滚转轴、俯仰轴和航向轴的陀螺仪随机漂移向量，则所述系统的状态方程为：

对f(x(k-1),(k-1))求取jacobi矩阵：

由状态转移函数可得状态的一步预测值：

计算状态向量一步预测误差方差矩阵：

p(k)＝φ(k,k-1)p(k,k-1)φ^t(k,k-1)+q(k)。

在一些实施方式中，设系统的观测向量为z(k)＝(ωbx(k)ωby(k)ωbz(k))^t，其中，ωbx(k)ωby(k)ωbz(k)表示载体坐标系中三轴加速度测量值，则所述系统的观测方程为：

对h(x(k)，k)求取jacobi矩阵，可得系统量测矩阵为：

由量测函数可得量测向量的一步预测值：

在一些实施方式中，计算状态增益矩阵：

k(k)＝p(k，k-1)h^t(k)[h(k)p(k，k-1)h^t(k)+r(k)]^-1。

在一些实施方式中，k时刻的状态向量估计值为：

在一些实时方式中，更新状态误差协方差矩阵为：

p(k)＝[i-k(k)h(k)]p(k，k-1)[i-k(k)h(k)]^t+k(k)r(k)k^t(k)。

在一些实施方式中，过程噪声协方差为：

量测噪声协方差矩阵为定常数对角阵。

在一些实施方式中，还包括以下步骤：

将所述ekf滤波器输出数据和修正后的加速度计输出数据进行融合求取姿态角，更新姿态信息。

本申请技术方案与现有技术相比，具有以下有益效果：

本申请的技术方案通过建立载体姿态测量模型，将三轴陀螺仪和三轴加速度计的输出量作为状态量，将三轴陀螺仪的输出做为观测量设计扩展卡尔曼滤波。应用载体的重力加速度和角速度进行时间更新，利用载体自身的角速度进行时间更新。从而有效降低了mems陀螺仪的漂移误差，解决了微机电系统用于载体姿态测量时精度低、易发散、易被干扰的问题，有效提高了姿态解算的精度。

通过数据融合算法，实现了利用加速度计对ekf滤波器输出结果的修正，进一步提高了系统的精度。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作一简单地介绍，显而易见地，下面描述中的附图是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

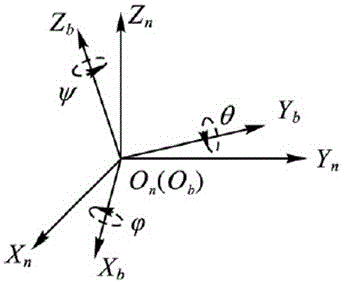
图1是本技术方案一实施方式的姿态角示意图；

图2是本申请技术方案一实施方式的方法流程图；

图3是本申请技术方案一实施方式的静止状态加高频振动实验的对比图；

图4是本申请技术方案一实施方式的以0.5hz的频率，±5°的幅度进行摇摆测试；

图5是本申请技术方案一实施方式的以50°/s的角速度进行旋转测试。

具体实施方式

为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

如图2所示，一种基于mems惯性传感器的载体动态姿态估计方法，包括以下步骤：

所用的传感器由一个三轴mems陀螺仪、一个三轴mems加速度计组成，传感器直接固联在载体上，各传感器内部测量轴相互正交且与载体坐标系重合，各传感器输出为三维矢量，角速度输出为ωb、加速度输出为ab。

步骤1：获取三轴加速度计数据并通过加速度计噪声模型进行处理。

其中，加速度计通过测量重力加速度在载体三轴上的分量来计算载体的姿态角。当载体做非匀速运动、机体存在较大振动时，会使姿态解算失效，因此需要对测量值进行校正：

加速度计的测量模型为其中：ab表示加速度计的测量值；ka表示标度系数矩阵；g＝(00-g)^t表示地理坐标系下的重力加速度矢量，g表示重力加速度常量；af表示载体的线性加速度矩阵；ba表示偏置误差矩阵；va表示测量噪声矩阵，为零均值的高斯白噪声，协方差为

步骤2：获取三轴陀螺仪数据并通过陀螺仪噪声模型进行处理。

陀螺仪通过测量载体的角速度，积分后既可以得到载体转动角度，但是由于mems陀螺仪制造工艺等因素，陀螺仪输出存在随机漂移和测量噪声误差。因此，单独使用陀螺仪进行姿态测量时，积分时间越长，姿态估计的误差越大，因此需要对测量值进行校正：

陀螺仪测量模型为ωb＝kωω+bω+vω,其中ωb表示陀螺仪的测量值；ω表示陀螺仪真值角速度；kω表示标度系数矩阵；bω表示陀螺仪随机漂移矩阵；vω表示测量噪声矩阵，为零均值的高斯白噪声，协方差为

步骤3：将以上三轴陀螺仪处理后的数据和三轴加速度计数据处理后的数据通过ekf滤波器进行处理，然后ekf滤波器输出数据和加速度计输出数据再进行融合，求取姿态角，更新姿态信息。

其中，ekf滤波器进行处理包括以下步骤：

构建卡尔曼滤波器系统模型：

其中：x(k)∈rⁿ表示k时刻系统的状态矢量；z(k)∈r^m表示k时刻系统的观测矢量；f(·)为n维矢量函数，h(·)为m维矢量函数，f(·)和h(·)对其自变量都是非线性的；w(k)∈rⁿ和v(k)∈r^m是协方差分别为q(k)和r(k)的过程噪声矢量；

建立扩展ekf滤波器方程：包括时间更新、测量更新；其中，时间更新包括系统状态量的先验估计和预测误差协方差矩阵的先验估计；量测更新包括系统的卡尔曼增益、系统状态量的后验估计和预测误差协方差矩阵的后验估计。具体描述如下：

1.初始化

计算状态初始值x(0)，设定过程噪声协方差q(k)、量测噪声协方差r(k)额误差方差矩阵p(0)。

2.时间更新

设系统的状态向量为：

x(k)＝(abx(k)aby(k)abz(k)ωx(k)ωy(k)ωz(k)bωx(k)bωy(k)bωz(k))^t

其中，abx(k)aby(k)abz(k)表示载体坐标系中三轴加速度测量值，ωx(k)ωy(k)ωz(k)表示载体坐标系中三轴陀螺仪测量值，bωx(k)bωy(k)bωz(k)分别为绕滚转轴、俯仰轴和航向轴的陀螺仪随机漂移向量，则所述系统的状态方程为：

对f(x(k-1)，(k-1))求取jacobi矩阵：

由状态转移函数可得状态的一步预测值：

计算状态向量一步预测误差方差矩阵：

p(k)＝φ(k，k-1)p(k，k-1)φ^t(k，k-1)+q(k)。

3.量测更新

设系统的观测向量为z(k)＝(ωbx(k)ωby(k)ωbz(k))^t，其中，ωbx(k)ωby(k)ωbz(k)表示载体坐标系中三轴陀螺仪测量值，则所述系统的观测方程为：

对h(x(k)，k)求取jacobi矩阵，可得系统量测矩阵为：

由量测函数可得量测向量的一步预测值：

计算状态增益矩阵：

k(k)＝p(k，k-1)h^t(k)[h(k)p(k，k-1)h^t(k)+r(k)]^-1。

k时刻的状态向量估计值为：

更新状态误差协方差矩阵为：

p(k)＝[i-k(k)h(k)]p(k，k-1)[i-k(k)h(k)]^t+k(k)r(k)k^t(k)。

其中，过程噪声协方差为：

量测噪声协方差矩阵为定常数对角阵。

而加速度计输出值和卡尔曼滤波输出姿态值之间的融合包括以下步骤：

一.判断两个惯性器件的值，其中，判定条件设为：

1.加速度计的矢量和与理想重力加速度g作比较；

2.三轴陀螺仪的输出值

(1)当|a-g|<0.01且ω<0.01时，载体姿态输出为：

其中，其中k为动态变化系数，att为卡尔曼输出的载体姿态角度

(2)当|a-g|<0.001g且ω<0.001g时，此时的载体姿态输出为

(3)当|a-g|>0.01g或ω>0.01g时att＝att，即完全置信卡尔曼滤波器的输出值。

二、判断陀螺仪输出前后差值：

当ωk,x-ωk-1,x<0.05且ωk,y-ωk-1,y<0.05且ωk,z-ωk-1,z<0.05时，完全置信加速度计的输出值，即

另外，需要说明的是：载体姿态运动模型的设置。

1.参考坐标系

定义载体坐标系为oxbybzb，该坐标系原点选为载体质心，xb轴沿载体横轴向右，yb轴沿载体纵轴向前，zb轴垂直载体指向上方，构成右手坐标系。定义地理坐标系oxnynzn作为导航坐标系，导航坐标系采用东北天坐标系，采用载体质心为原点。姿态角的定义如图1所示，绕x轴旋转对应俯仰角pitch、绕y轴旋转对应横滚角roll、绕z轴旋转对应偏航角yaw，分别为三轴欧拉角φ、θ、ψ。

2.坐标系间的转换

导航坐标系和载体坐标系两者可以通过姿态矩阵进行转换。本技术方案采用的是y→x→z的旋转顺序，分别旋转角度得到。则载体坐标系和导航坐标系之间的旋转关系可表示为：

其中：

式(1)为坐标转换矩阵，即姿态矩阵，对于坐标转换矩阵可知重力加速度在载体坐标上的三轴矢量为：

其中，

由式(1)(2)可得载体三轴与水平面的夹角分别为：

实施例2效果实验对比

本文设置了三组实验进行对比，以验证本文算法的有效性，三组实验分别是：1)静止状态加高频振动实验，结果如图3所示；2)以0.5hz的频率，±5°的幅度进行摇摆测试，结果如图4所示；3)以50°/s的角速度进行旋转测试，结果如图5所示。每组实验都是极三种姿态计算算法：利用加速度计的姿态解算算法(g-a)，采用fir滤波的姿态解算算法(fir)，以及本申请设计的ekf滤波算法(ekf)，通过对比检验三种算法的不同情况下的性能。

由图3可见，在震动状态下，g-a算法有较大的波动，误差达到3°左右，而fir算法虽然解决了振动引起的角度变化的问题，但是z轴的角度有较大误差，而ekf算法则是有效的修正了z轴的角度，并且将角度的变化幅度控制在0.3°之内，能够准确的获得载体的姿态信息。

由图4和图5可得，在旋转和摇摆的运动状态下，g-a算法和fir算法存在较大的误差，尤其是在摇摆运动状态下，g-a算法和fir算法存在最大3-5°的误差，不能够准确的描述载体的姿态和运动状态；ekf算法则能够准确的对载体的姿态进行描述，在这两种运动状态下误差小于0.2°，能够有效的反应当前时刻的载体姿态。

本申请技术方案与现有技术相比，具有以下有益效果：

由于利用mems传感器求解载体姿态时主要存在以下几种误差：1)传感器的安装误差；2)陀螺仪的漂移和线性度误差；3)加速度计和陀螺仪的零位误差；所以通过加速度计噪声模型对加速度计数据进行处理，通过陀螺仪噪声模型对陀螺仪数据进行处理，将以上三轴陀螺仪处理后的数据和三轴加速度计数据处理后的数据通过ekf滤波器处理，稳定准确地得到动态载体的姿态信息。

其次，本技术方案通过建立载体姿态测量模型，将三轴陀螺仪和三轴加速度计的输出量作为状态量，将三轴陀螺仪的输出做为观测量设计扩展卡尔曼滤波。应用载体的重力加速度和角速度进行时间更新，利用载体自身的角速度进行时间更新。从而有效降低了mems陀螺仪的漂移误差，解决了微机电系统用于载体姿态测量时精度低、易发散、易被干扰的问题，有效提高了姿态解算的精度。在此基础上进行多传感信息融合，进一步稳定准确地得到动态载体的姿态信息。

最后应说明的是：以上实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的精神和范围。