一种离轴式激光雷达几何因子的校正方法与流程

本发明涉及一种激光雷达技术领域，特别涉及一种离轴式激光雷达几何因子的校正方法。

背景技术：

激光雷达是一种主动式的现代光学遥感设备，具有很高的时空分辨率，可以连续地探测大气中气溶胶粒子的光学特性垂直分布特征，较好的弥补以往探测仪器的不足。

激光雷达的工作原理是激光器向大气中发射线偏振光，激光传输路径上的大气气溶胶或云等物质散射后，其偏振态和光强会发生相应的变化，通过光学接收系统捕获后向散射设信号，再经过对原始信号的去噪、反演等处理便可以得到反映大气气溶胶或云的物理特性的图谱。

同轴式光学发射系统和离轴式光学发射系统是目前两种比较常用的发射系统类型。对于离轴式系统来说，采用实验的方法校正几何因子是目前比较常用的一种方式，但这种方式理论上要求天空干洁无气溶胶，对天气状况要求较高，实际的校正效果受到天气的影响，存在一定程度的不确定性。

技术实现要素：

为了解决上述现有技术中的不足，本发明的目的在于提供一种离轴式激光雷达几何因子的校正方法，该校正方法能够在无需依赖天气状况的情况也能够对激光雷达的几何因子进行校正。

本发明解决其技术问题所采用的技术方案为：一种离轴式激光雷达几何因子的校正方法，包括以下步骤：

s1、将激光雷达的望远镜接收信号区域分为盲区、过渡区以及完全接收区；

其中，所述盲区是激光器的后向散射信号不在望远镜有效接收范围之内的区域，所述过渡区是激光器的后向散射信号的部分信号被望远镜有效接收范围的区域，所述完全接收区是激光器的后向散射信号完全被望远镜有效接收范围之内的区域；

s2、在所述盲区、过渡区、完全接收区中，分别得出三个区域内的几何因子，其中，

在所述盲区中，几何因子为o＝0；

在所述过渡区中，几何因子0＜o＜1；

在所述完全接收区中，几何因子为o＝1；

s3、对所述过渡区中的几何因子进行修正，其修正过程为：

a、得出望远镜接收到的任意位置处的后向散射信号强度i1，以及激光器发出的激光在相同位置处的信号强度i2；

b、根据上述得到的望远镜接收到的信号强度i1以及激光器发出的激光在相同位置处的信号强度i2，得出理论几何因子o′，其中，o′＝i1/i2；

c、根据高斯分布公式，得出几何因子的权重w；

d、根据几何因子o与权重w的关系，得出几何因子o的精确值，其中，o＝w*i1/i2。

2.根据权利要求1所述的离轴式激光雷达几何因子的校正方法，其特征在于，在步骤s3中，将o′＝i1/i2使用o′＝s/s′代替，其中，s是望远镜接收到的后向散射信号强度为i1位置处的光斑面积，s′是激光器发出的激光在信号强度为i2处的光斑面积。

采用上述技术方案，本发明与现有技术相比，具有以下有益效果：

1.本发明不依赖于天气情况，可以在任何情况下对离轴式激光雷达的几何因子进行校正；

2.本发明相较于传统技术中采用实验法的校正方法，免去了需要采集数据、数据拟合等复杂的过程，简单高效。

附图说明

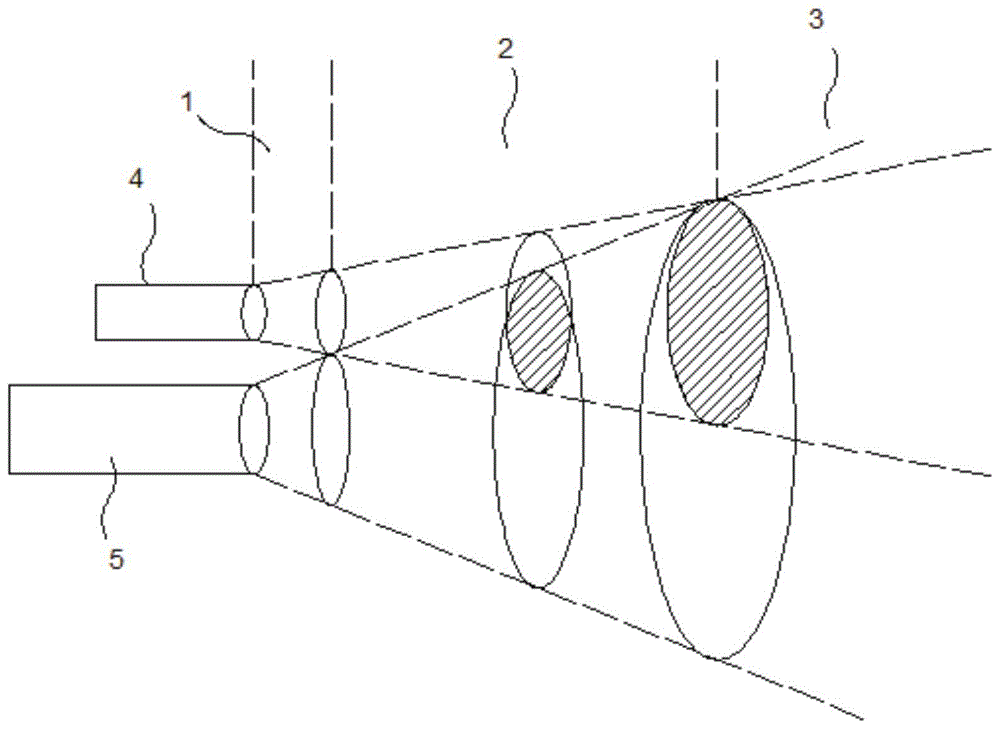
图1是本发明的离轴激光雷达的几何因子示意图；

图2是本发明的望远镜接收信号的光斑示意图a；

图3是本发明的望远镜接收信号的光斑示意图b；

图4是本发明的望远镜的信号接收比例关系图；

图5是本发明的望远镜接收信号的光斑质心位置示意图；

图6本发明的过渡区的几何因子的高斯分布示意图。

具体实施方式

下面结合附图和实施例对本申请作进一步的详细说明。可以理解的是，此处所描述的具体实施例仅仅用于解释相关发明，而非对该发明的限定。另外还需要说明的是，为了便于描述，附图中仅示出了与发明相关的部分。

需要说明的是，在不冲突的情况下，本申请中的实施例及实施例中的特征可以相互组合。下面将参考附图并结合实施例来详细说明本申请。

本发明公开了一种离轴式激光雷达几何因子的校正方法，该方法相较于传统校正中采用的实验法，能够免去依赖天气状况才可进行校正的麻烦，而且免去了需要采集数据、数据拟合等复杂的过程，简单高效。包括以下步骤：

s1、如图1所示，将激光雷达的望远镜接收信号区域分为盲区1、过渡区2以及完全接收区3；

其中，盲区1是激光器4的后向散射信号不在望远镜5有效接收范围之内的区域，过渡区2是激光器4的后向散射信号的部分信号被望远镜5有效接收范围的区域，完全接收区3是激光器4的后向散射信号完全被望远镜5有效接收范围之内的区域。

s2、在盲区1、过渡区2、完全接收区3中，分别得出三个区域内的几何因子，其中，

在盲区1中，由于望远镜5完全接收不到激光器4的向后散射信号，因而在盲区1中，其几何因子为o＝0；

在过渡区2中，由于望远镜5只能接收到激光器4的部分向后散射信号，而该部分向后散射信号的强度i1小于激光器4发出的激光在相同位置时的光信号强度i2，在过渡区2中，望远镜5接收到的信号比例随着距离r改变，在不同距离上有着不同的比例，在过渡区2中这个比例的范围为0＜o＜1，随着距离的增加，接收的比例也逐渐增大，因而其几何因子0＜o＜1；

在完全接收区3中，由于望远镜5接收到激光器4的全部向后散射信号，因而，在完全接收区3中，其几何因子为o＝1。

由上可知，在盲区1以及完全接收区3中，其几何因子是固定不变的，因而在盲区1和完全接收区3中，其几何因子是不需要进行校正的，而在过渡区2中，随着过渡区3中任意位置到激光器的距离的增加，其几何因子是逐渐变化，因而，在过渡区2中，其几何因子是个变量，需要对其进行修正。

s3、对过渡区2中的几何因子进行修正，其修正过程为：

a、得出望远镜5接收到的任意位置处的后向散射信号强度i1，以及激光器4发出的激光在相同位置处的信号强度i2；

b、根据上述得到的望远镜5接收到的信号强度i1以及激光器4发出的激光在相同位置处的信号强度i2，得出理论几何因子o′，其中，o′＝i1/i2；

c、根据高斯分布公式，得出几何因子的权重w；

d、根据几何因子o与权重w的关系，得出几何因子o的精确值，其中，o＝w*i1/i2。

在步骤s3中，将o′＝i1/i2使用o′＝s/s′代替，其中，s是望远镜接收到的后向散射信号强度为i1位置处的光斑面积，s′是激光器发出的激光在信号强度为i2处的光斑面积。

下面结合附图，对修正过渡区2中的几何因子进行具体的描述。

在过渡区2中，望远镜5接收到的信号的光斑如图2所示，也就是说，望远镜5接收到的信号的光斑面积s，可以分成两部分，分别是s1和s2，如图3所示，其中：

s＝s1+s2。

在这里面s1和s2是望远镜5的主光轴距离d、激光器发散角α、望远镜接收角β和激光传输距离l的函数，他们的关系可以表达为：

s1＝func1(d^-1，α，β，l)

s2＝func2(d^-1，α，β，l)

由此可以得到望远镜5接收部分的光斑面积s的表达式为：

s＝func1(d^-1，α，β，l)+func2(d^-1，α，β，l)

在上式中，

s1＝func1(d^-1，α，β，l)

s2＝func2(d^-1，α，β，l)

也可以表达为：

其中，

在上式中，α1是激光器4发射的激光发散角，α2是望远镜5的接收视场角，l是激光器4发出的激光到达位置到激光雷达的距离，d0是激光器4的光轴与望远镜5的光轴之间的距离。其中，在本实施例中，α和α1均表示激光器4发射的激光发散角，两者数值相等；α2与β均表示望远镜5的接收视场角，两者数值相等。

在本实施例中，距离激光雷达为l处的光斑面积s的表达式为：

s＝π(α1*l)²；

因而，在本实施例中，理论上的几何因子的表达式为：

通常，不同位置的激光光强分布符合高斯分布，不同位置的激光光强是光斑半径r的函数，对于接收范围内的光斑能量的计算做一个近似，定义有效接受区域径向长度的中点为质心p，用该点的能量代表这个区域的平均能量，质心p位置如图5所示。同时，激光器4发出的激光能量是以高斯分布的形式分布的，其能量分布图如图6所示，因而，在过渡区2中，激光光斑半径为r处的高斯分布权重的表达式为：

上式中，r是激光光斑的最大半径，r是传输距离为l处的激光光斑半径。

假设质心p到激光器主光轴中心间距为r′，由此得到的最终几何因子为：

其中，是质心p位于激光器4主光轴时的权重。

由此可见，通过本发明的校准方法来校准激光雷达的几何因子，可以不用依赖天气情况，在任何情况下对离轴式激光雷达的几何因子进行校正，而且免去了需要采集数据、数据拟合等复杂的过程，简单高效。

以上描述仅为本申请的较佳实施例以及对所运用技术原理的说明。本领域技术人员应当理解，本申请中所涉及的发明范围，并不限于上述技术特征的特定组合而成的技术方案，同时也应涵盖在不脱离所述发明构思的情况下，由上述技术特征或其等同特征进行任意组合而形成的其它技术方案。例如上述特征与本申请中公开的(但不限于)具有类似功能的技术特征进行互相替换而形成的技术方案。

除说明书所述的技术特征外，其余技术特征为本领域技术人员的已知技术，为突出本发明的创新特点，其余技术特征在此不再赘述。