一种基于圆形扫描的机载激光雷达最大测距能力和测角精度的检验方法与流程

本发明属于激光雷达测量系统的检验方法领域，特别涉及该领域中的一种基于圆形扫描的机载激光雷达最大测距能力和测角精度的检验方法。

背景技术：

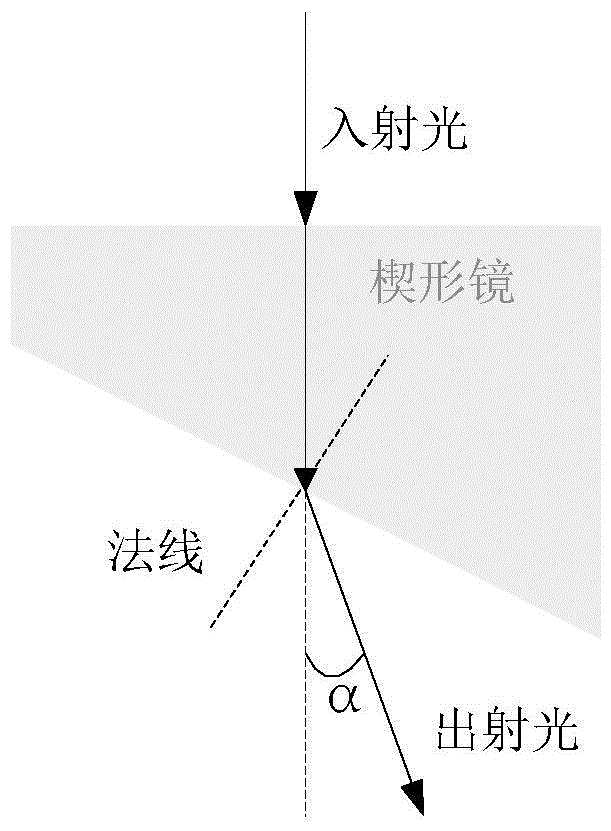
基于圆形扫描的机载激光雷达采用单波束工作方式，如图1所示，激光器每次只发射一路光束，经楔形镜折射后沿楔形镜最厚的位置射出，在通过前部的镜面后对外部目标物发射。楔形镜固定在旋转轴承上，电机转动时轴承带动楔形镜一起转动，激光的折射光束也随着楔形镜最厚的部位进行圆形的旋转，在雷达的发射镜面形成扫描圆。

激光雷达通过发射激光束，并接收目标反射的回波信号展开测量作业。以回波信号接收时间与激光束发射时间之间的差值，计算目标物与激光雷达之间的距离，再结合激光束发射时楔形镜的旋转位置、激光折射角等信息，计算目标物相对于激光雷达的方向及位置信息。

激光雷达工作时的直接测量值包括激光束发射至接收的时间差t以及激光束发射时的镜面位置角θ；楔形镜折射角α理论上为固定值，但是如果楔形镜的安装存在偏差，将导致在不同的θ角位置对应的α值不相等。

激光雷达测量数据解算中，以时间t计算目标点距离l；以距离l、镜面位置角θ、楔形镜折射角α解算目标点在激光雷达三维坐标系中的x、y、z坐标值。因此，激光雷达的目标测量错误主要由测量值t、θ以及固定值α的异常引起。

技术实现要素：

本发明所要解决的技术问题就是提供一种基于圆形扫描的机载激光雷达最大测距能力和测角精度的检验方法。

本发明采用如下技术方案：

一种基于圆形扫描的机载激光雷达最大测距能力和测角精度的检验方法，其改进之处在于，包括如下步骤：

(1)最大测距能力检验步骤：

(11)选择可以测量到约1000米、约3100米远处目标的激光雷达架设位置，并将激光雷达架设在该位置，架设基座可旋转也可固定；

(12)使用激光测距机测量2个不同距离处的无遮挡目标，分别为约1000m处的目标a和约3100m处的目标b，激光测距机的测量值作为距离真值参与检验；

(13)设置激光雷达采用最大输出功率，然后用100khz的工作频率对目标a、b展开原地测量，测量过程中，激光雷达的楔形镜不旋转，激光束沿固定的镜面位置角发射，激光雷达设备可随其架设基座原地旋转；

(14)测量完成后进行数据的解算，并根据测量数据的解算结果判断激光雷达的测距能力，判断方法如下：

(141)如激光雷达在100khz频率工作时，对目标a、b的测量均存在大量回波数据，且距离解算结果与激光测距机的测量值相等，则认为在100khz工作时可达到3000米的最大测距值；

(142)如激光雷达在100khz频率工作时，测量数据的解算结果对目标a、b均有明显的距离值，且目标a处距离解算结果与激光测距机的测量值相等，但目标b处距离解算结果为约100米或约1600米，则可认为激光雷达的测量能力可达3000米，但该处数据解算存在错误；

(143)如激光雷达在100khz频率工作时，测量数据的解算结果仅有约1000米的距离值，不存在与目标b相关的距离解算结果，即约100米、约1600米和约3100米，则认为激光雷达的测量能力不满足3000米的测距要求，其测距能力不足；

(2)镜面位置角检验步骤：

(21)激光雷达前部镜面在安装集成时共使用了8个螺钉，在检验中选择螺钉的中心点作为检验点，分别定义为点a、b、c、d、e、f、g、h；

(22)将激光雷达的发射光轴转动至检测点a，使得雷达的发射光轴与a点的中心在同一平面上，定点采集数据，随后将激光雷达的发射光轴依次转动至检测点b-h，进行定点数据采集；

(23)解析在点a-h采集的激光雷达数据，获得在每个检测点的镜面位置角θa、θb、θc、θd、θe、θf、θg、θh；

(24)依次计算相邻点之间的角度差θb-θa、θc-θb、θd-θc、θe-θd、θf-θe、θg-θf、θh-θg、θa-θh，在计算θa-θh时，取θa＝360°，如有角度差≠45°的情况，则可认为镜面位置角存在异常；

(25)重复(22)-(24)三次，如均有角度差＝45°，则认为镜面位置角正确；

(3)楔形镜折射角检验步骤：

(31)选择一个较高的平整房顶，将激光雷达竖直放置，使其前部镜面面向房顶；

(32)设置激光雷达的发射功率为最小功率，并在前部镜面贴上遮光纸，阻挡发射激光束的部分能量，以实现近距离检测；

(33)设置激光雷达以低速转动并采集数据，进行数据解算；

(34)数据解算完成后先去掉距离值差异较大的点，包括但不限于柱子和侧壁，在距离值相等的点中选择4组发射角相差180°的数据作为检验数据，定义为a-h点；

(35)对于距离测量值相等的a、e点，如有满足za＝ze；xa＝-xe；ya＝-ye的坐标解算结果，则可认为激光雷达在ae轴的折射角相等；

(36)分别计算b与f、c与g、d与h点的检测数据，如有不满足上述计算结果的情况，则认为楔形镜折射角存在异常；

(37)重复(34)-(36)，选择检测点3次，如均满足上述计算结果，则认为楔形镜发射角正确。

本发明的有益效果是：

本发明所公开基于圆形扫描的机载激光雷达最大测距能力和测角精度的检验方法，可有效检验激光雷达在加工、装配阶段可能出现的多种结构性误差以及点云解算中存在的算法错误，发现激光雷达在设计、组装及数据处理方面存在的问题，避免因激光雷达自身测量数据错误，导致机载激光雷达系统飞行作业后建立的目标地域的三维模型失真。

采用本发明的检验方法，在完成激光雷达测距精度的检验后，按照从(1)至(3)的步骤依次检验，在确认上一个参数检验正确后，再展开下一个参数的检验，可以实现对激光雷达最大测距能力、镜面位置角以及楔形镜折射角的精确检验，进而实现对激光雷达设备中存在问题的精确定位。

附图说明

图1是楔形镜的折射方式示意图；

图2是激光雷达光束发射方式的示意图；

图3是本发明方法的流程示意图；

图4是本发明方法检验激光雷达最大测距能力的原理图；

图5是距离解算的间隔时间示意图；

图6是镜面x0y坐标系中的检验点分布图；

图7是楔形镜折射角检验点分布图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图和实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。

最大测距能力是目前激光雷达产品的一个重要参数，是机载激光雷达实现中、高空测量作业的基本要求，也是本实施例涉及的激光雷达产品的一个重要考核指标。

如图3所示，本实施例的技术方案以基于圆形扫描的机载激光雷达的工作原理为依据，设计并实现了最大测距能力检验方法、镜面位置角检验方法及楔形镜折射角检验方法，使用这些方法不仅可以在激光雷达设备自身组装时发现结构装配偏差，也可以在设备研制时优化波形解算算法，并帮助确定激光雷达在不同工作环境下的最佳作业参数。

上述的最大测距能力检验方法、镜面位置角检验方法及楔形镜折射角检验方法均以激光雷达测距精度为基础，在雷达测距精度满足要求的前提下展开检验。雷达测距精度的检验采用全站仪测量的方法实现，具体细节此处不再赘述。

(1)最大测距能力检验：

最大测距能力即激光雷达的最大作业距离，本实施例中涉及的激光雷达设备在100khz工作时最大作业距离为3km。

设激光雷达发射激光束至接收到回波的时间为t，则激光雷达至目标的距离为：

l＝c×t/2，c＝光速；

工作频率在100khz的激光雷达，激光束的发射间隔时间为10^-5秒，而激光雷达接收到3km处目标回波信号的时间为：

可知，激光雷达在对3km远处的目标发射激光束后，并不能在下一个激光束发射前接收到目标的回波信号。而3km处目标回波信号的接收时间正好与第二个激光束发射的时间重合，这可能会导致回波信号不能被正确接收，为避免因发射、接收冲突而造成测距失败，在实际检验过程中选择距离激光雷达略大于3km的目标进行测量。

如图5所示，采用激光雷达对约3100m远处的目标b进行测量时，接收到目标b的回波时距离发射激光束(主波)的间隔时间为2.067×10^-5秒，相对于主波后第一个激光束的间隔时间为1.067×10^-5秒，相对于主波后第二个激光束的间隔时间为0.067×10^-5秒。

在进行目标距离解算时，只有找到目标b的回波信号对应的发射激光束(主波)，才能获得正确的目标距离(约3100米)；如将主波信号认定为主波后的第一个激光束，则距离计算值为约1600米；如将主波信号认定为主波后的第二个激光束，则距离计算值为约100米。

另外，如果因为目标b距离激光雷达过远，不足以产生有效的回波，则测量数据中无法解算出与目标b的距离相关的距离值，即距离解算结果中不存在约100米、约1600米、约3100米的数值。

具体方法如下：

(11)选择可以测量到约1000米、约3100米远处目标的激光雷达架设位置，并将激光雷达架设在该位置，架设基座可旋转也可固定；

(12)使用激光测距机测量2个不同距离处的无遮挡目标，分别为约1000m处的目标a和约3100m处的目标b，激光测距机的测量值作为距离真值参与检验；

(13)如图4所示，设置激光雷达采用最大输出功率，然后用100khz的工作频率对目标a、b展开原地测量，测量过程中，激光雷达的楔形镜不旋转，激光束沿固定的镜面位置角发射，激光雷达设备可随其架设基座原地旋转；

(14)测量完成后进行数据的解算，并根据测量数据的解算结果判断激光雷达的测距能力，判断方法如下：

(141)如激光雷达在100khz频率工作时，对目标a、b的测量均存在大量回波数据，且距离解算结果与激光测距机的测量值相等，则认为在100khz工作时可达到3000米的最大测距值；

(142)如激光雷达在100khz频率工作时，测量数据的解算结果对目标a、b均有明显的距离值，且目标a处距离解算结果与激光测距机的测量值相等，但目标b处距离解算结果为约100米或约1600米，则可认为激光雷达的测量能力可达3000米，但该处数据解算存在错误；可认为目标点对激光雷达产生了回波，激光功率及光路设计满足要求，造成距离解算异常的原因仅为波形解算的算法错误。

(143)如激光雷达在100khz频率工作时，测量数据的解算结果仅有约1000米的距离值，不存在与目标b相关的距离解算结果，即约100米、约1600米和约3100米，则认为激光雷达的测量能力不满足3000米的测距要求，其测距能力不足；测距能力不足是由于发射激光束的能量不足以到达远处的目标，或远处目标产生的回波太弱无法返回激光雷达，造成这种问题的主要原因是激光雷达的发射功率不足，需要对激光的发射装置进行改进。

(2)镜面位置角检验：

激光雷达内部的伺服电机驱动楔形镜以平行于镜面的方式旋转，雷达发射的激光束随着楔形镜的旋转形成以楔形镜中心为圆心、半径固定的激光发射圆。

激光雷达内部电机转动时，由电机带动轴承匀速旋转，编码器通过读取固定在轴承上的光栅获得镜面位置角，镜面位置角错误将导致测量目标在激光雷达的x0y平面内位置解算错误。导致镜面位置角错误的原因如下：光栅与轴承不同轴；光栅码异常、编码器故障；电机转轴与编码器中心不同轴。镜面位置角为激光雷达设备直接读取的数据，检验中只需对激光雷达前部镜面按照角度进行等分，并分析等分后相邻点之间的夹角。

具体方法如下：

(21)激光雷达前部镜面在安装集成时共使用了8个螺钉，这8个螺钉的位置正好满足均匀分布的特征，在检验中选择螺钉的中心点作为检验点(具体位置如图6所示)，分别定义为点a、b、c、d、e、f、g、h；

(22)转动激光雷达，将激光雷达的发射光轴转动至检测点a(即激光雷达楔形镜最厚的位置位于点a)，使得雷达的发射光轴与a点的中心在同一平面上，定点采集数据，随后将激光雷达的发射光轴依次转动至检测点b-h，进行定点数据采集；

(23)解析在点a-h采集的激光雷达数据，获得在每个检测点的镜面位置角θa、θb、θc、θd、θe、θf、θg、θh；

(24)依次计算相邻点之间的角度差θb-θa、θc-θb、θd-θc、θe-θd、θf-θe、θg-θf、θh-θg、θa-θh，在计算θa-θh时，取θa＝360°，如有角度差≠45°的情况，则可认为镜面位置角存在异常；

(25)重复(22)-(24)三次，如均有角度差＝45°，则认为镜面位置角正确；

(3)楔形镜折射角检验：

如图2所示，楔形镜折射角指激光束相对于前部镜面的出射角度，以激光雷达的镜面中心为原点，目标点在激光雷达0xyz坐标系中z方向的坐标为：

z＝l×cosα，α为楔形镜折射角；

x、y轴方向的坐标分别为：x＝l×sinα×cosθ，y＝l×sinα×sinθ，θ为镜面位置角；由于激光雷达数据解算时按照楔形镜折射角为固定值的方法计算，如楔形镜折射角出现异常，将导致目标点在0xyz坐标系中的坐标值解算错误。造成楔形镜折射角异常的原因可能是镜面中心o与楔形镜法线之间存在位置偏差，也可能是驱动电机的转轴与楔形镜的法线之间存在偏差。

由于激光雷达楔形镜折射角理论上为固定值，可采用对平面旋转测量的方法检验。使用激光雷达对平面进行扫描时，如有两个点的扫描角满足θ2＝θ1+180°，则这两个点的解算数据也应满足z1＝z2、x1＝-x2、y1＝-y2。选取多组满足θ2＝θ1+180°的扫描点，如数据解算结果均有z1＝z2、x1＝-x2、y1＝-y2，则可认为激光雷达的楔形镜折射角固定。如存在测量距离l相同且θ2＝θ1+180°，但解算结果不满足z1＝z2、x1＝-x2、y1＝-y2的扫描点，则认为楔形镜折射角存在异常。

具体方法如下：

(31)选择一个较高的平整房顶，将激光雷达竖直放置，使其前部镜面面向房顶；

(32)设置激光雷达的发射功率为最小功率，并在前部镜面贴上遮光纸，阻挡发射激光束的部分能量，以实现近距离检测；

(33)设置激光雷达以低速转动并采集数据，进行数据解算；

(34)数据解算完成后先去掉距离值差异较大的点(柱子和侧壁等测距值异常的点)，在距离值相等的点中选择4组发射角相差180°的数据作为检验数据，如附图7中的a-h点；

(35)对于距离测量值相等的a、e点，如有满足za＝ze；xa＝-xe；ya＝-ye的坐标解算结果，则可认为激光雷达在ae轴的折射角相等；

(36)分别计算b与f、c与g、d与h点的检测数据，如有不满足上述计算结果的情况，则认为楔形镜折射角存在异常；

(37)重复(34)-(36)，选择检测点3次，如均满足上述计算结果，则认为楔形镜发射角正确。