一种用于补偿六维力传感器的方法与流程

本发明涉及一种用于补偿六维力传感器的方法，属于自动化领域。

背景技术：

目前，在机械臂的应用过程中，机械臂末端的六维力传感器负责对机械臂的受力情况进行实时监测，同时作为运动规划的参考，要求能够同时监控三个力分量与三个力矩分量的变化，并实时将力与力矩的全部信息反馈到中央控制器，便于中央控制器对机械臂进行控制。其中，使用六维力传感器的过程是通过将所有支路采集的数据利用特定的算法进行解算，转化为空间载荷值的过程。

但在实际应该过程中，发现六维力传感器存在如下问题：当六维力传感器的刚性要求较大，且力和力矩的测量量程接近1:1时，六维力传感器的维间耦合严重，所得的解算结果精度较低。经检索，目前现有技术中未发现有解决该问题的方法，只能使用该精度较低的解算结果进行应用。

技术实现要素：

有鉴于此，本发明提出一种用于补偿六维力传感器的方法，在不增加六维力传感器结构复杂度的同时，通过补偿算法，对六维力传感器的解算结果进行补偿，提高六维力传感器的解算精度。

一种用于补偿六维力传感器的方法，获得由x轴、y轴和z轴方向的力和力矩六个元素组成的初始解算矩阵；

根据六维力传感器初始解算矩阵的值与校准力值的差异，确定力与力矩之间的预设关系；将初始解算矩阵中获得的元素代入预设关系中，获得力的补偿量，并对初始解算矩阵中的力进行补偿；

根据六维力传感器初始解算矩阵的值与校准力值的差异，确定力矩与力矩之间的预设关系；将初始解算矩阵中获得的元素代入预设关系中，获得力矩的补偿量；并对初始解算矩阵中的力矩进行补偿；

其中，所述力与力矩之间的预设关系包括第一预设关系和第二预设关系，其中，第一预设关系是反映主影响力矩对x轴、y轴和z轴方向的力产生的影响关系；第二预设关系是反应次影响力矩对x轴、y轴和z轴方向的力产生的影响关系；其中，主影响力矩和次影响力矩根据实际应用分析场景确定。

较佳地，所述初始解算矩阵由预设的校准矩阵和传感器的灵敏度电压差的乘积获得。

较佳地，在获得第一预设关系时，以x轴方向的力矩作为主影响力矩，解算x轴方向的力矩对x轴、y轴和z轴方向的力产生的影响关系，则其第一预设关系为：

其中，δfx1为x轴方向的力矩对x轴方向的力的预设关系所对应的补偿，δfy1为x轴方向的力矩对y轴方向的力之间的预设关系所对应的补偿，δfz1为x轴方向的力矩对z轴方向的力之间的预设关系所对应的补偿，mx0为所述初始解算矩阵中x轴方向的力矩，ki'为系数，i’＝1，2，…，9，d1、d2、d3为常数项。

较佳地，在获得第二预设关系时，以y轴方向和z轴方向的力矩作为次影响力矩，解算y轴方向和z轴方向的力矩对x轴方向、y轴方向和z轴方向的力产生的影响关系，则其第二预设关系为：

δfx2＝e1×my0²+e2×my0×mz0+e3×mz0²+e4×my0+e5×mz0+f1(4)

δfy2＝e6×my0²+e7×my0×mz0+e8×mz0²+e9×my0+e10×mz0+f2(5)

δfz2＝e11×my0²+e12×my0×mz0+e13×mz0²+e14×my0+e15×mz0+f3(6)

其中，δfx2为y轴方向和z轴方向的力矩对x轴方向的力之间预设关系所对应的补偿，δfy2为y轴方向和z轴方向的力矩对y轴方向的力之间预设关系所对应的补偿，δfz2为y轴方向和z轴方向的力矩对z轴方向的力之间预设关系所对应的补偿，my0和mz0为所述初始解算矩阵中的y轴方向和z轴方向的力矩，ei″为系数，i″＝1，2，…，15，f1、f2、f3为常数项。

较佳地，在根据力与力矩之间的预设关系，获得补偿初始解算矩阵中的力之后，对初始解算矩阵中的力进行补偿的方法为：

fx＝fx0+δfx1+δfx2(7)

fy＝fy0+δfy1+δfy2(8)

fz＝fz0+δfz1+δfz2(9)

其中，fx为最终广义解算矩阵中x轴方向的力，fy为最终广义解算矩阵中y轴方向的力，fz为最终广义解算矩阵中z轴方向的力；fx0为初始解算矩阵中x轴方向的力，fy0为初始解算矩阵中y轴方向的力，fz0为初始解算矩阵中z轴方向的力；δfx1、δfy1、δfz1可通过第一预设关系求得；δfx2、δfy2、δfz2可通过第二预设关系求得。

较佳地，所述力矩与力矩之间的预设关系为：

mx＝mx0+g1×my0²+g2×my0×mz0+g3×mz0²+g4×my0+g5×mz0+h1(10)

my＝my0+g6×mx0²+g7×mx0×mz0+g8×mz0²+g9×mx0+g10×mz0+h2(11)

mz＝mz0+g11×mx0²+g12×mx0×my0+g13×my0²+g14×mx0+g15×my0+h3(12)

其中，mx为最终广义解算矩阵中x轴方向的力矩，my为最终广义解算矩阵中y轴方向的力矩，mz为最终广义解算矩阵中z轴方向的力矩；mx0为初始解算矩阵中x轴方向的力矩，my0为初始解算解算矩阵中y轴方向的力矩，mz0为初始解算解算矩阵中z轴方向的力矩，gt为系数，t＝1，2，…，15，h1、h2、h3为常数项。

有益效果：

1、本发明通过设定力矩与力的预设关系，以及力矩与力矩之间的预设关系，实现了对初始解算矩阵中力矩与力的补偿，进而提高了测量精度。

2、在分析力矩与力的预设关系时，本发明不仅考虑了产生主要影响的力矩对不同方向的力的影响进行补偿，还考虑了产生次要影响的力矩对不同方向的力进行补偿。，该方法能够使测量结果更加精准。

附图说明

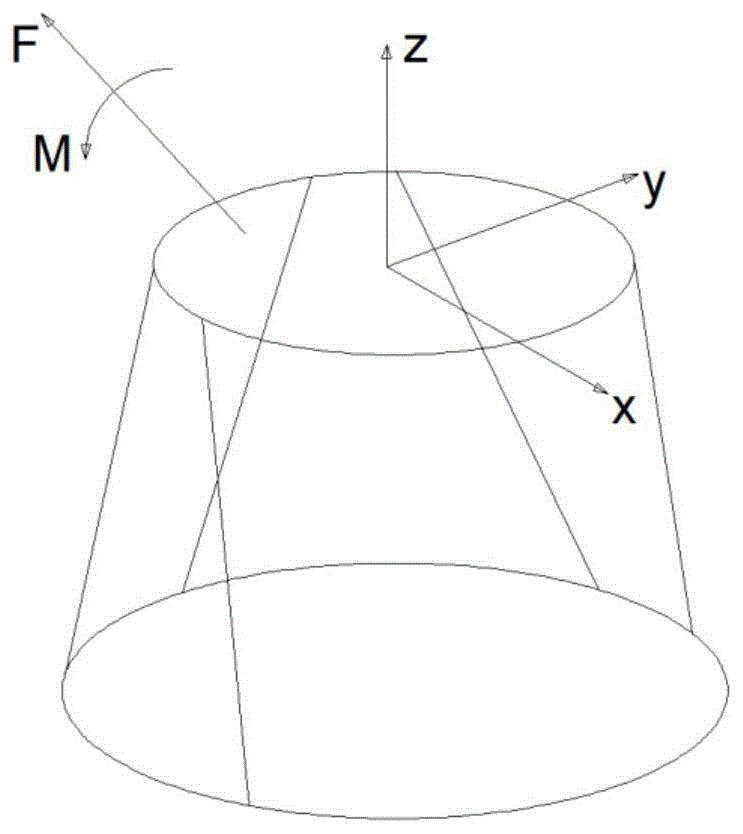
图1是本发明的六维力传感器的结构示意图；

图2是本发明用于补偿六维力传感器的方法流程示意图；

图3是本发明利用力矩与力的预设关系补偿初始解算矩阵中的力的流程示意图。

具体实施方式

下面结合附图并举两个实施例，对本发明进行详细描述。

本发明提供一种用于补偿六维力传感器的方法，流程图如图2所示，具体包括如下步骤：

步骤一、获得初始结算矩阵

初始解算力矩中包括六个元素，分别是三个不同方向的力和三个不同方向的力矩。如三个方向的力呈正交关系；三个方向的力矩呈正交关系。图1为本公开实施例提供的一种六维力传感器的结构示意图。图中示例性的示出了力f、力矩m、x轴、y轴、z轴。

其初始解算矩阵的计算公式为：

f6×1＝c6×6×δu灵敏度6×1(13)

其中，f6×1为初始解算矩阵且fx0、fy0和fz0代表初始解算矩阵中x轴、y轴和z轴方向的力，mx0、my0和mz0初始解算矩阵中x轴、y轴和z轴方向的力矩；

c6×6为校准矩阵且c11、c22、c33、c44、c55、c66为校准矩阵常数；

δu灵敏度6×1为传感器电压差且δu灵敏度＝u载荷i-u0i，为传感器零点输出基准电压，u载荷i，为传感器采集的数据，i＝1～6；

将公式(1)进一步演化，则获得初始解算矩阵的具体公式为：

步骤二、如图2所示，利用六维力传感器初始解算矩阵的值与校准力值的差异确定的力矩与力之间的预设关系补偿初始解算矩阵中的力，利用六维力传感器初始解算矩阵的值与校准力值的差异确定的力矩与力矩之间的预设关系补偿初始解算矩阵中的力矩，获得最终广义解算矩阵，进而提高六维力传感器的解算进度。

如图3所示，在步骤二中，最终广义解算矩阵中包括6个元素，分别为三个方向的力和三个方向的力矩。利用初始解算矩阵中的力矩和初始解算矩阵中的力的预设关系补偿初始解算矩阵中的力，以获得最终广义解算矩阵中的力；利用初始解算矩阵中力矩之间的预设关系补偿初始解算矩阵中的力矩，以获得最终广义解算矩阵中的力矩。本实施例中，可首先利用初始解算矩阵中力矩与初始解算矩阵中力之间的预设关系补偿初始解算矩阵中的力，获得最终广义解算矩阵中的力，再利用初始解算矩阵中力矩之间的预设关系补偿初始解算矩阵中的力矩，获得最终广义解算矩阵中的力矩；或者，首先利用初始解算矩阵中力矩之间的预设关系补偿初始解算矩阵中的力矩，获得最终广义解算矩阵中的力矩，再利用初始解算矩阵中力矩与初始解算矩阵中力之间的预设关系补偿初始解算矩阵中的力，获得最终广义解算矩阵中的力。

其具体实现方法为：

a、利用初始解算矩阵中的力矩和初始解算矩阵中的力的预设关系补偿初始解算矩阵中的力，以获得最终广义解算矩阵中的力；其中，上述预设关系包括第一预设关系和第二预设关系，第一预设关系是对某方向的力的解算产生主要影响的某一方向的力矩与x轴方向、y轴方向和z轴方向的力之间的预设关系，可反映单一方向的力矩对单一方向的力的影响。在实际应用中，可以根据实际应用分析场景选择某一轴，分析该轴方向的力矩对x轴方向、y轴方向和z轴方向的力的解算产生的影响。例如，选择x轴方向的力矩对x轴方向、y轴方向和z轴方向的力的解算产生主要影响；或选择y轴方向的力矩对x轴方向、y轴方向和z轴方向的力的解算产生主要影响；再或选择z轴方向的力矩对x轴方向、y轴方向和z轴方向的力的解算产生主要影响。

第二预设关系为对某方向的力的解算产生次要影响的一个或两个方向的力矩与x轴方向、y轴方向和z轴方向的力之间的预设关系，可反映一个或两个方向力矩对某一个的力的影响。同样的，第二预设关系在进行解算时，选择分析除第一预设关系中选择的轴以外的一个或多个轴所对应方向力矩分别对x轴方向、y轴方向和z轴方向的力的解算产生的影响。例如，选择y轴方向和z轴方向的力矩对x轴方向、y轴方向和z轴方向的力产生影响；或选择x轴方向和z轴方向的力矩对x轴方向、y轴方向和z轴方向的力产生影响。再或选择y轴方向和x轴方向的力矩对x轴方向、y轴方向和z轴方向的力产生影响。

首先，根据第一预设关系，获得待补偿初始解算矩阵中的力。本实施例仅以x轴方向的力矩对x轴方向、y轴方向和z轴方向的力的解算产生主要影响为例进行说明。第一预设关系为：

其中，δfx1为x轴方向的力矩对x轴方向的力的预设关系所对应的补偿，δfy1为x轴方向的力矩对y轴方向的力之间的预设关系所对应的补偿，δfz1为x轴方向的力矩对z轴方向的力之间的预设关系所对应的补偿，mx0为所述初始解算矩阵中x轴方向的力矩，ki′(i’＝1至9)为系数，d1、d2、d3为常数项。

之后，根据第二预设关系，获得待补偿初始解算矩阵中的力。由于上述实施例中在获得第一预设关系时选择以x轴方向的力矩对x轴方向、y轴方向和z轴方向的力进行解算，所以在获得第二预设关系时，将以y轴方向和z轴方向的力矩对x轴方向、y轴方向和z轴方向的力产生影响。

第二预设关系为：

δfx2＝e1×my0²+e2×my0×mz0+e3×mz0²+e4×my0+e5×mz0+f1；(18)

δfy2＝e6×my0²+e7×my0×mz0+e8×mz0²+e9×my0+e10×mz0+f2；(19)

δfz2＝e11×my0²+e12×my0×mz0+e13×mz0²+e14×my0+e15×mz0+f3；(20)

其中，δfx2为y轴方向和z轴方向的力矩对x轴方向的力之间预设关系所对应的补偿，δfy2为y轴方向和z轴方向的力矩对y轴方向的力之间预设关系所对应的补偿，δfz2为y轴方向和z轴方向的力矩对z轴方向的力之间预设关系所对应的补偿，my0和mz0为所述初始解算矩阵中的y轴方向和z轴方向的力矩，ei″(i″＝1至15)为系数，f1、f2、f3为常数项。

则最终广义解算矩阵中的力为：

fx＝fx0+δfx1+δfx2；(21)

fy＝fy0+δfy1+δfy2；(22)

fz＝fz0+δfz1+δfz2；；(23)

其中，fx为最终广义解算矩阵中x轴方向的力，fy为最终广义解算矩阵中y轴方向的力，fz为最终广义解算矩阵中z轴方向的力；fx0为初始解算矩阵中x轴方向的力，fy0为初始解算矩阵中y轴方向的力，fz0为初始解算矩阵中z轴方向的力；δfx1、δfy1、δfz1可通过第一预设关系求得；δfx2、δfy2、δfz2可通过第二预设关系求得。

b、初始解算矩阵中力矩与力矩之间的预设关系为：

mx＝mx0+g1×my0²+g2×my0×mz0+g3×mz0²+g4×my0+g5×mz0+h1(24)

my＝my0+g6×mx0²+g7×mx0×mz0+g8×mz0²+g9×mx0+g10×mz0+h2(25)

mz＝mz0+g11×mx0²+g12×mx0×my0+g13×my0²+g14×mx0+g15×my0+h3(26)

其中，mx为最终广义解算矩阵中x轴方向的力矩，my为最终广义解算矩阵中y轴方向的力矩，mz为最终广义解算矩阵中z轴方向的力矩；mx0为初始解算矩阵中x轴方向的力矩，my0为初始解算解算矩阵中y轴方向的力矩，mz0为初始解算解算矩阵中z轴方向的力矩，gt(t＝1至15)为系数，h1、h2、h3为常数项。

上述方法最终实现了对初始结算矩阵中力和力矩的补偿，提高了测量精度。

综上所述，以上仅为本发明的较佳实施例而已，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。