一种精密单点定位的方法与流程

本发明涉及精密单点定位技术领域，具体为一种精密单点定位的方法。

背景技术：

在卫星导航定位中，采用伪距定位的方法定位精度只能达到米级，而载波相位测量的精度为0.2～0.3mm，其测距精度比测码伪距的精度要高2～3个数量级，因此载波相位测量在高精度定位中得到了广泛的应用。但是载波是一种没有任何标记的余弦波，接收机的鉴相器只能测量载波相位不足一周的部分，而整周数是不确定的。此外整周计数部分还可能产生跳变的问题，这就使得载波相位测量的数据处理工作变得较为复杂。在不依靠基准站的情况下，精密单点定位(ppp)对整周进行估计，并采用载波相位作为测量量，可以显著提供定位精度。

下面的论文列举了精密单点定位的原理及一些实现方法：

koubaj,herouxp.precisepointpositioningusingigsorbitandclockproducts[j].gpssolutions,2001,5(2):12–28

gaoy,shenx.improvingambiguityconvergenceincarrierphase-basedprecisepointpositioning[c].ionnationaltechnicalmeeting,saltlakecity,2001

zhangxiaohong,lipan,zuoxiang.kinematicpreciseorbitdeterminationbasedonambiguity-fixedppp[j].geomaticsandinformationscienceofwuhanuniversity,2013,38(9):1009–1013(张小红,李盼,左翔.固定模糊度的精密单点定位几何定轨方法及结果分析[j].武汉大学学报·信息科学版,2013,38(9):1009–1013.)

ahmedf,vaclavovicp,teferlefn,etal.comparativeanalysisofreal-timeprecisepointpositioningzenithtotaldelayestimates[j].gpssolutions,2014:1–13。

精密单点定位方法的缺陷是收敛慢，往往需要经过半个小时以上的平滑才能收敛到所需要的精度。有一些相关专利对上述技术进行了改进，但也都主要是通过改进分析方法提高收敛的准确度和可靠性的判断，对提高定位精度和减少收敛时间没有帮助，如专利“实时精密单点定位方法”。

造成精密单点定位方法缺陷的原因分析如下：

在卫星导航测量中的观测量存在各种误差，两个频率上的伪距测量量和载波相位测量量如下公式：

上述公式中，λ1和λ2是波长，ρ表示卫星与接收机的几何距离，与接收机位置相关的信息就包含在其中。上角标i表示第i颗卫星。

dtr和dpr1，dpr1表示接收机的钟差和伪距硬件延迟，这一部分跟卫星无关，可以通过增加观测量去除。同理，dφr1和dφr2也可以通过增加观测量去除。表示卫星钟差，可以通过精密星历去除。是卫星上的码硬件延时，属于已知量。是对流层延时，可以通过分析大气中的干湿分量分别计算去除。ε是测量误差，属于零均值的高斯白噪声，可以通过平滑和滤波的方式减小，并反映在定位误差上。因此，通过上述观测量进行定位时，需要计算的量就是电离层延时以及两个频率上的整周模糊度n1及n2。由于卫星上的相位延时和包含了未知的调制载波的初始相位信息，因此属于未知量，在计算中归并到整周模糊度n1及n2上，导致n1及n2不再是整数，而是一个实数。

在普通定位方法中，仅用到伪距观测量p1和p2，但是由于伪距观测量测量噪声很大，导致定位结果不够准确。高精度定位会用观测噪声很小的载波相位观测量l1和l2，但其中含有未知的整周模糊度n1及n2。

因此，在进行精密单点定位的计算时，需要解算n1及n2，并且解算或者去除

由于和并不独立，tec表示自由电子密度，f1和f2分别是两个频点的载波频率，所以通过一些组合的观测量可以达到上述目的。这些组合的观测量包括：

无电离层组合：

无几何组合或宽巷组合：l4＝l1-l2,p4＝p1-p2

宽巷线性组合：

m-w组合：

上述组合观测量中宽巷线性组合通常用于检测周跳，但无法消除任何一项未知数，因此通常不用于解算。而其他组合各有优缺点：

无电离层组合可以消除未知的电离层延时，但是等效波长为0，无法求解组合的整周模糊度。

宽巷组合无法完全消除电离层影响。

m-w组合虽然不包含电离层，也具有较长的等效波长用于求解模糊度，但引入伪距观测量使得观测误差大大增加。

精密单点定位通过综合使用以上组合观测量，能够达到消除或解算未知量的目的，但是由于求解实数整周模糊度存在准确性问题以及观测量误差大的问题，造成滤波和解算需要很多历元才能成功收敛。

技术实现要素：

本发明的目的在于提供一种精密单点定位的方法，以解决上述背景技术提出的不能准确计算电离层参数并估算整周模糊度，不能直接准确估算电离层延时大小，整周模糊度数值准确度低，影响收敛速度更快完成高精度定位解算的问题。

为实现上述目的，本发明提供如下技术方案：一种精密单点定位的方法，包括如下步骤：

s1：射频前端，经过天线接收卫星信号；

s2：基带信号处理，经过信号放大，下变频和ad转换后变成数字基带信号；

s3：原始观测生成，在基带信号处理单元中对信号进行跟踪处理，根据跟踪的结果产生不同频点的原始观测量，包括伪距测量量p1和p2和载波相位测量量l1和l2或φ1和φ2(由于两个频点的载波波长λ1和λ2是已知量，所以两者可以互相转换)；

s4：组合观测量求解整周模糊度n1和n2；

s5：进行定位解算。

优选的，所述s1：射频前端，经过天线接收卫星信号；s2：基带信号处理，经过信号放大，下变频和ad转换后变成数字基带信号；s3：原始观测生成，在基带信号处理单元中对信号进行跟踪处理，根据跟踪的结果产生不同频点的原始观测量，包括伪距测量量p1和p2和载波相位测量量l1和l2或φ1和φ2(由于两个频点的载波波长λ1和λ2是已知量，所以两者可以互相转换)构成基带信号处理单元。

优选的，所述组合观测量求解整周模糊度n1和n2，由各种组合观测量的观测方程可以看出，组合观测量为原始观测量的线性组合。在卫星导航信号中，由于各个信号的载波频率都是1.023mhz的整数倍(如伽利略e5信号两个频率分别为1176.45mhz＝1150x1.023mhz，1207.14＝1180x1.023mhz)；

因此以频率为系数的线性组合可以视为整数系数的线性组合；

在这种情况下，作为整数的整周模糊度n1和n2的整数系数组合依然为整数；

选取两组组合观测量(如其中一种实施例可以选取宽巷组合和宽巷线性组合)，则组合伪距观测量与组合载波相位观测量的差将只包含组合的整周模糊度与测量噪声(即在该实施例中为l4-p4和l5-p5)；

由于测量噪声为时间无关，因此可以通过多个观测量的平滑去除，由此可以计算得到组合的整周模糊度(在该实施例中可以定义为n4和n5)；

在测量噪声平滑到足够小以后，对计算得到的组合整周模糊度取整即可得到真正的整数值组合整周模糊度；

进而计算得到整周模糊度n1和n2；

由于相对于其他高精度单点定位方法采用两个间隔较远的频点，本发明中使用的boc信号的两个频点距离很近(如伽利略的e5信号间隔为30.69mhz)，等效的波长较长，因此有利于计算整数的整周模糊度。

优选的，所述定位解算，在得到整周模糊度n1和n2后，带入到载波相位观测量的表达式中后，仅有的未知量就剩下与接收机位置相关的几何距离ρ和接收机本地钟差dtr；

因此可以通过传统的最小二乘或卡尔曼滤波的方式进行求解，进一步平滑观测噪声；

通过对定位结果的误差统计和计算(如判断卡尔曼滤波过程中的状态噪声)，在定位结果的误差小于期望值以后，则可以将精确的定位结果进行输出。

与现有技术相比，本发明的有益效果是：该精密单点定位的方法对卫星导航信号中的boc信号进行接收，利用boc信号的频谱具备两个统一调制但又处于不同频点上的两个能量瓣(或称为边带)的特点，对两个不同频率信号进行统一接收，通过该方法，可以解决原有方法不能准确计算电离层参数并估算整周模糊度的问题，较准确地对电离层延时进行估算，可以更快更可靠地实现高精度单点定位，并且能够直接准确估算电离层延时大小，求解整数值的整周模糊度，提高了准确度，提高收敛速度更快完成高精度的定位解算。

附图说明

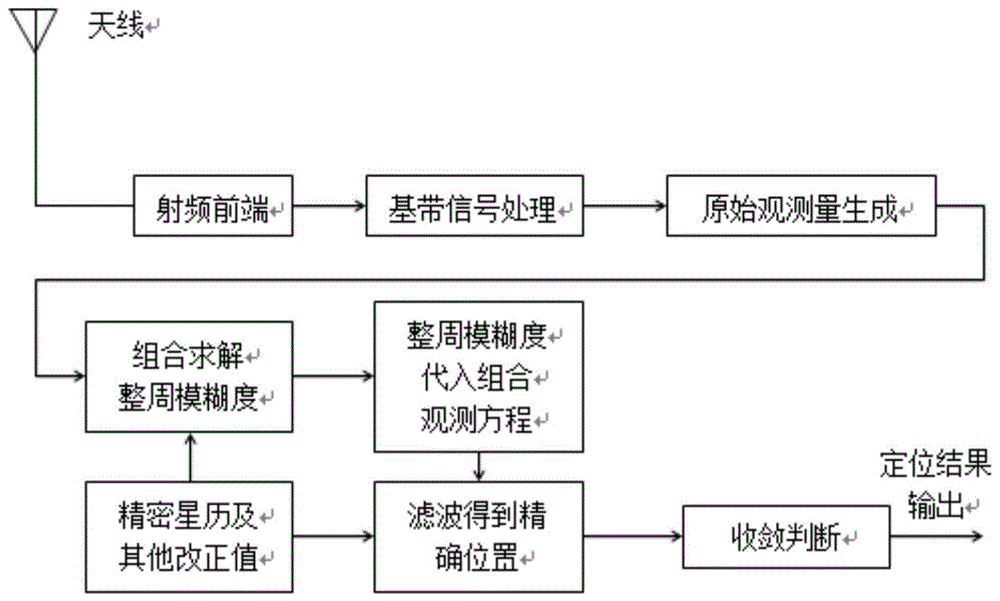
图1为本发明数据处理方法流程示意图；

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

请参阅图1，本发明提供一种技术方案：一种精密单点定位的方法，包括如下步骤：

s1：射频前端，经过天线接收卫星信号；

s2：基带信号处理，经过信号放大，下变频和ad转换后变成数字基带信号；

s3：原始观测生成，在基带信号处理单元中对信号进行跟踪处理，根据跟踪的结果产生不同频点的原始观测量，包括伪距测量量p1和p2和载波相位测量量l1和l2或φ1和φ2(由于两个频点的载波波长λ1和λ2是已知量，所以两者可以互相转换)；

s1：射频前端，经过天线接收卫星信号；s2：基带信号处理，经过信号放大，下变频和ad转换后变成数字基带信号；s3：原始观测生成，在基带信号处理单元中对信号进行跟踪处理，根据跟踪的结果产生不同频点的原始观测量，包括伪距测量量p1和p2和载波相位测量量l1和l2或φ1和φ2(由于两个频点的载波波长λ1和λ2是已知量，所以两者可以互相转换)构成基带信号处理单元；

接收处理的卫星导航信号为宽带boc信号，boc信号在现代卫星导航信号中被普遍采用，比如说伽利略的e5信号就采用了altboc(15，10)的调制方法，而gps和北斗的卫星导航信号也采用或准备采用包括boc(15，10)或boc(15，2.5)这样的宽带boc信号；

宽带boc信号的特点是调制时作为一个统一的复数信号进行调制，接收时既可以当作一个单一的信号，也可以把两个边带分别当作bpsk调制的普通信号进行接收；

接收端在射频前端把信号当作一个单独的宽带信号进行处理，并变成一个包含全部两个边带的宽带数字中频信号，然后在基带信号处理中分别恢复两个载波，并比较两个载波间的相位差得到两者的相对延时关系；

由于在接收端，两个边带的信号会分别剥离进行bpsk调制的码，因此在等效处理时可以把调制端的bpsk调制和接收端的bpsk解调去掉，把信号简化为两个相位同步的单频信号：

s＝sin(2πf1t)+sin(2πf2t)。到达接收端时，由于电离层的影响，两个频点的信号分别具有不同的延时，也就是接收端收到的信号为

其中及是两个频率经过电离层造成的相位延时；

在射频前端经过下变频后，得到基带信号：

其中fl和分别时本地载波的频率和初始相位，将两个频点的信号进行分离，并分别与同步的本地数字载波sl1＝sin[2π(f1-fl)t]和sl2＝sin[2π(f1-fl)t]进行相干解调后，可以得到和

由于用于下变频的本地载波具有未知的初始相位导致接收端在恢复载波时，无法单独恢复和

通过同步解调的方式比较两者的相位差可以计算得到

根据电离层相位延时的公式可以得到两个不同频率载波的相位差为

以伽利略的e5信号为例，上述公式中f1和f2分别取值1176.45mhz和1207.14mhz，根据测量得到的δφ可以计算自由电子密度tec并进一步计算得到两个频点的电离层延时，由于用于计算电离层延时的观测值δφ的测量噪声很小(通常可以达到百分之一到千分之几周)，由此计算得到的电离层延时误差在分米级以下，且噪声也是时间无关的高斯白噪声，可以在后续的滤波计算中进行消除；

原始观测量的生成与一般接收机处理方法中原始观测量的生成基本一致，由于对电离层延时进行了测量估计，可以在原始观测量中预先将电离层延时予以去除；

通过比较载波测量量l1和l2的表达式可以发现，两者的不同点在忽略测量噪声εφ时，不同的部分有电离层延时dtiono、卫星端硬件延时dφs以及接收端硬件延时dφr，考虑到对于boc信号由于是作为复数信号统一调制的，接收端进行接收时也是作为一个整体信号进行的解调，所以信号经过的是同样的硬件电路，因此两个不同频率信号的卫星端硬件延时dφs以及接收端硬件延时dφr是一致的，所不同的就只有电离层延时，因此，在将原始观测量中的电离层延时去除后，将计算得到的电离层延时进行线性组合后，将仅包含未知量n1和n2；

s4：组合观测量求解整周模糊度n1和n2；

所述组合观测量求解整周模糊度n1和n2，由各种组合观测量的观测方程可以看出，组合观测量为原始观测量的线性组合。在卫星导航信号中，由于各个信号的载波频率都是1.023mhz的整数倍(如伽利略e5信号两个频率分别为1176.45mhz＝1150x1.023mhz，1207.14＝1180x1.023mhz)；

因此以频率为系数的线性组合可以视为整数系数的线性组合；

在这种情况下，作为整数的整周模糊度n1和n2的整数系数组合依然为整数；

选取两组组合观测量(如其中一种实施例可以选取宽巷组合和宽巷线性组合)，则组合伪距观测量与组合载波相位观测量的差将只包含组合的整周模糊度与测量噪声(即在该实施例中为l4-p4和l5-p5)；

由于测量噪声为时间无关，因此可以通过多个观测量的平滑去除，由此可以计算得到组合的整周模糊度(在该实施例中可以定义为n4和n5)；

在测量噪声平滑到足够小以后，对计算得到的组合整周模糊度取整即可得到真正的整数值组合整周模糊度；

进而计算得到整周模糊度n1和n2；

由于相对于其他高精度单点定位方法采用两个间隔较远的频点，本发明中使用的boc信号的两个频点距离很近(如伽利略的e5信号间隔为30.69mhz)，等效的波长较长，因此有利于计算整数的整周模糊度。

s5：进行定位解算；

所述定位解算，在得到整周模糊度n1和n2后，带入到载波相位观测量的表达式中后，仅有的未知量就剩下与接收机位置相关的几何距离ρ和接收机本地钟差dtr；

因此可以通过传统的最小二乘或卡尔曼滤波的方式进行求解，进一步平滑观测噪声；

通过对定位结果的误差统计和计算(如判断卡尔曼滤波过程中的状态噪声)，在定位结果的误差小于期望值以后，则可以将精确的定位结果进行输出。

尽管参照前述实施例对本发明进行了详细的说明，对于本领域的技术人员来说，其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。