一种无物方控制点的GNSS近景摄影测量装置的制作方法

本实用新型涉及gnssrtk测量技术和无控制数字近景摄影测量技术，具体涉及一种无物方控制点的gnss近景摄影测量装置，属于工程测量中的细部测量领域。

背景技术：

随着全球卫星定位系统(gnss)技术的不断发展，gnss技术在测绘领域的使用越来越广泛。gnss主要是通过接收卫星信号进行测量，在有遮挡或部分遮挡的情况下，gnss就不能使用或者测量精度无法保证。

近景摄影测量是一种瞬间获取被测物体大量物理信息和几何信息的测量手段，它不接触、不伤及测量目标，不干扰被测物自然状态，可在恶劣条件下作业。

传统的近景摄影测量方式，能够达到很高的精度，但是需要布置物方控制点，并不适用精度要求稍低但需要操作简单快捷的测量需求。

微电子技术和半导体技术方面的突破，超大规模的集成电路和数字传感器技术的迅速发展，出现了许多新型的高清摄像头，其优点在于价格比数码相机低廉，体积小，能够与gnss接收机集成在一起。

在测量建筑物或者其他立体结构时，遇到遮挡或信号不好的情况，将集成了高清摄像头的gnss接收机放置于信号好的位置并进行坐标测量，该位置称为摄站点，同时在该位置上用摄像头拍摄建筑物影像。将数个摄站上的三维坐标数据和影像数据进行处理，在不同影像上选取同一目标点，建立立体模型，在模型上对待测点进行立体量测。

技术实现要素：

本实用新型的目的在于设计一种无物方控制点的gnss近景摄影测量装置，其能间接解决gnss测量时信号不佳的问题和近景摄影测量需要布置控制点的问题。

本实用新型通过集成gnss接收机、高清摄像头、个人数字助理(pda，personaldigitalassistant)、对中杆等硬件设备，无需布设控制点，通过处理gnss坐标和影像数据，直接获取待测目标点的三维坐标。

为达到上述目的，本实用新型提供了一种无物方控制点的gnss近景摄影测量系统，包括了gnss接收机、高清摄像头、个人数字助理pda、对中杆和连接架。所述高清摄像头集成于gnss接收机中。所述pda通过蓝牙对gnss接收机和高清摄像头进行操控。所述对中杆将与gnss接收机连接。所述连接架可将对中杆、pda连夹在一起。

本实用新型的操作步骤为：

(1)将所述对中杆竖直立于能够接收到卫星信号的某摄站点上，该摄站点距离目标点10m～20m为宜；

(2)所述gnss接收机记录该摄站点的三维坐标；

(3)所述高清摄像头在该摄站点上记录目标点的影像；

(4)在三个不共线的位置上，都以步骤(1)至步骤(3)进行操作，获取三个摄站点的坐标信息和和三张同一目标点的影像；

(5)在pda中将坐标数据和影像数据进行处理，对待测目标点进行立体量测，解算其三维坐标。

与现有的技术相比，本实用新型有如下优点：

本实用新型的无物方控制点的gnss近景摄影测量装置，集成了全球卫星定位技术、近景摄影测量技术、无线通信技术与一身的快速测量坐标的装置。在无信号遮挡的地方直接使用gnss测量点的坐标，若遇到信号遮挡严重但视线通视，则可使用上述方法对目标点进行摄影测量。该装置有效解决了近景摄影测量需要布设物方控制点的问题，又充分利用了近景摄影测量不需要接触目标点就可以进行立体量测的优势，弥补了gnss测量存在信号遮挡的缺陷，减少野外测量的工作量，提高碎部测量的工作效率和自动化程度。

附图说明

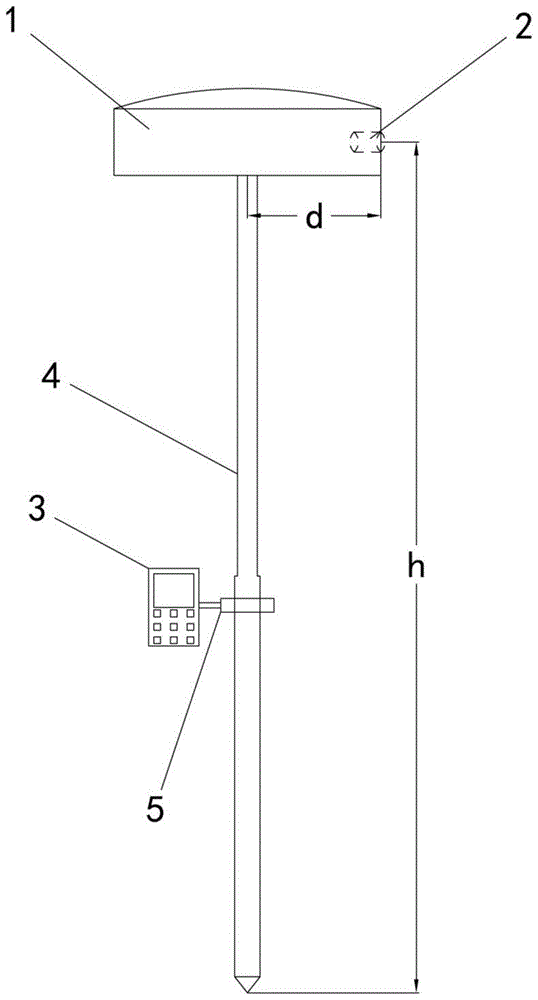
图1为本实用新型结构示意图。

图2为对中杆中心与摄影中心平面位置关系图。

图3为gnss近景摄影测量装置外业作业图。

图中：1-gnss接收机；2-高清摄像头；3-pda；4-对中杆；5-连接架。

具体实施方式

以下结合附图对本实用新型做进一步描述：

如图1所示，本实用新型的近景摄影测量装置，包括gnss接收机1、高清摄像头2、个人数字助理pda3、对中杆4和连接架5。高清摄像头2集成在gnss接收机1内部靠边缘的位置，gnss接收机1中心与高清摄像头2中心位于同一水平面，两者的水平距离为d，摄像头镜头与gnss接收机1边缘接合，组成带有摄像头的gnss接收机；将带有摄像头的gnss接收机安装于对中杆4之上，gnss接收机1中心与对中杆4中心在竖直方向上重合，对中杆4可伸缩并且量出gnss接收机1中心与地面的高差h；个人数字助理pda3通过蓝牙对gnss接收机1和高清摄像头2进行操控，人数字助理pda3有键盘操作和电容式触摸屏操作两种方式，方便人机交互；人数字助理pda3可通过连接架5固定在对中杆4上，也可手持，连接架5可拆卸。

如图2所示，对中杆4中心与摄影中心平面位置关系图。对中杆4中心用o表示，摄影中心(摄像头中心)用s表示，对中杆中心与摄影中心的连线线段为os，os的坐标方位角用αos表示，os的长度为d。

实施例

如图3所示，要测量某建筑物的特征点坐标，由于建筑物所处位置gnss信号受遮挡严重，不能直接使用gnss接收机进行测量，因此采用gnss近景摄影测量装置进行测量。

一种无物方控制点的gnss近景摄影测量装置，将所述对中杆竖直立于能够接收到卫星信号的某摄站点上，并且与目标点通视，如图3所示。利用pda操控gnss接收机和高清摄像头，获取1摄站点至3摄站点的坐标数据和目标点的影像数据，要求在于这三个摄站点不能共线。

在pda中将采集到的gnss坐标数据和影像数据进行处理，解算相对定向元素和绝对定向元素，最后进行目标点的立体量测，数据的主要解算过程如下：

摄像头检校

应用高清数码摄像头进行近景摄影测量工作前，必须对其进行严格的检校，以恢复摄影中心与像片之间的相对几何关系。

对摄像头进行检校的主要内容就是获取摄像头的基本信息、镜头畸变参数和内方位元素(x0，y0，f)等参数。

相对定向模块

建立坐标系时以左像片的像空间坐标系作为像空间辅助坐标系，记为s1-x1y1z1；过右摄影中心建立另一像空间辅助坐标系s2-x2y2z2，两者相应坐标轴相互平行。此时，像点a1，a2在各自的像片坐标系中的坐标分别为(x1，y1)，(x2，y2)，像空间辅助坐标系中的坐标为(x1，y1，z1)，(x2，y2，z2)，而s2在s1-x1y1z1中的坐标为(bx，by，bz)。由此，共面条件方程可以表示为

(1)式中：(x0，y0，f)为像片的内方位元素；这里认为两张像片具有相同的内方位元素；旋转矩阵r由第二张像片相对于第一张像片的3个旋转角ω,κ的函数组成，a1,a2,a3,b1,b2,b3,c1,c2,c3为r中的9个方向余弦。

本文采用直接求解bx，by，bz这3个基线分量，由于bx，by，bz只有2个独立参数，因此需要加入1个约束条件，即3个基线分量的平方和为定值，如式(4)的第一个式子所示。

本文采用基于正交旋转矩阵的共面条件方程式求解，以旋转矩阵r中的9个方向余弦作为未知参数。

旋转矩阵r是正交矩阵，即rr^t＝r^tr＝rr^-1＝i，列出由9个方向余弦组成的6个正交条件，建立6个条件方程，如式(4)的后6个式子所示。

需要解算12个未知参数，即3个基线分量和9个旋转矩阵中的元素，最终加入7个条件方程式，包括1个基线分量的约束条件，6个正交矩阵约束条件。误差方程式为：

v＝ax-l(2)

x^t＝[dbxdbydbzda1da2da3db1db2db3dc1dc2dc3]

l＝-f0＝x2y1bz+x1z2by+y2z1bx-y1z2bx-x1y2bz-x2z1by

直接利用式(1)对12个未知数求导得到的误差方程式系数

对3个基线分量及9个旋转矩阵元素建立的7个条件方程为

(4)式中：b表示为基线长度，由于比例在模型连接中将会调整并在绝对定向中求出，因此这里可以设置为任意常数。附加条件方程式为

cx+w＝0(5)

式中：w为条件方程常数项矩阵。此时m张相片可建立(m-1)个如式(2)的误差方程，最后加入如式(5)的7个误差方程式，利用附加条件的间接平差方法解算12个未知参数。

解算出了这12个未知参数，也就相当于求出右像片相对左像片的相对方位元素。现以左像片的像空间坐标系作为像空间辅助坐标系，则左、右像片的相对方位元素为：

左片1：xs1＝0，ys1＝0，zs1＝0，ω1＝0，κ1＝0

右片2：xs2＝bx2，ys2＝by2，zs2＝bz2，ω2，κ2

右片3：xs3＝bx3，ys3＝by3，zs3＝bz3，ω3，κ3

……

绝对定向模块

绝对定向的基本关系式为：

式中，(xtp,ytp,ztp)为模型点的地面摄影测量坐标，λ为模型缩放比例因子，ai，bi，ci(i＝1,2,3)是坐标轴系3个转角φ，ω，k的方向余弦，(xp,yp,zp)为同一模型点的摄影测量坐标，δx、δy、δz为坐标原点的平移量。

这7个参数λ，φ，ω，k，δx，δy，δz称为绝对定向元素。

传统上求解这7个绝对定向元素是利用已知控制点的摄影测量坐标和它的地面摄影测量坐标，从绝对定向的关系式出发，求解上述7个绝对定向元素。

本实用新型的求解绝对定向元素算法中，是利用摄影中心的摄影测量坐标(xps,yps,zps)和它的地面摄影测量坐标(xtps,ytps,ztps)，关系式如下：

摄影中心的摄影测量坐标(xps,yps,zps)为像片的相对方位线元素，即上述左片1(xs1,ys1,zs1)，右片2(xs2,ys2,zs2)，右片3(xs3,ys3,zs3)，……

摄影中心的地面摄影测量坐标(xtps,ytps,ztps)是右手坐标系，其横轴为x轴，纵轴为y轴；摄影中心的地面测量坐标(xts,yts,zts)是左手坐标系，其横轴为y轴，纵轴为x轴。地面摄影测量坐标系和地面测量坐标系可以通过简单的数学关系相互转换。

下面介绍摄影中心的地面测量坐标(xts,yts,zts)的获取方式。

如图1所示，gnss接收机所测得的地面点坐标为(xg,yg,zg)，对中杆的底端到摄影中心的高为h，对中杆中心到摄影中心的水平距离为d。如图2所示，对中杆中心与摄影中心的连线线段os的坐标方位角用αos表示，线段os的磁方位角用amos表示，磁偏角用δp表示，子午线收敛角用γp表示。

在gnss接收机中，内置一个电子罗盘，用于测量线段os的磁方位角amos，δp和γp都可根据实地地区找到对应的参数。

线段os的坐标方位角可表示为αos＝amos+δp-γp(8)

摄影中心的地面测量坐标可表示为(xg+dsinαos,yg+dcosαos,zg+h)。

由于电子罗盘的局限性，其测量的磁方位角会存在误差，其测角中误差最大为3°对中杆中心到摄影中心的水平距离为d为8cm，d的中误差为0.5cm，故摄影中心点的地面测量坐标带有6.4mm左右的点位中误差。

在gnss近景摄影测量中，至少在3个不共线位置上对同一目标进行交相摄影，获取了至少3组数据(摄站点坐标和在该点拍摄的影像作为一组数据)。

由相对定向获取了摄影中心的摄影测量坐标(xps,yps,zps)，即上述左片1(xs1,ys1,zs1)，右片2(xs2,ys2,zs2)，右片3(xs3,ys3,zs3)。

将摄影中心的3个地面测量坐标转换成3个地面摄影测量坐标。

在公式(7)中，有7个未知数，即7个绝对定向参数，至少需要7个方程，本方法中涉及了3个摄影中心点，可列9个方程，有多余观测值，按最小二程法平差求解。

采用重心化坐标求解绝对定向元素

坐标重心化是一种很常用的数据预处理方法，其目的有两个。

一是减少模型点坐标在计算过程中的有效位数，以保证计算的精度。

二是采用了重心化坐标以后，可使法方程的系数简化，个别项的数值变成0，部分未知数可以分开求解，从而提高了计算速度。

立体量测模块

多片空间前方交会

近景摄影测量中，摄影中心、物点和对应像点的共线方程式为：

式(9)中：f为相机主距；像方坐标系下，(x，y)为像点坐标，(x0，y0)为主点坐标，(δx，δy)为畸变误差；物方坐标系下，(x，y，z)为物点坐标，(xs，ys，zs)为摄影中心坐标，ai，bi，ci(i＝1,2,3)是角元素的函数，表示主光轴的朝向。

近景摄影测量处理中，像点坐标(x，y)是主要的一类观测值。

将共线方程式线性化，得到像点坐标改正数方程式为：

式(11)是一个迭代运算过程。其中(vx，vy)为像点坐标改正数；(x)和(y)是像点坐标前一次迭代运算结果的近似值，像点坐标对每个变量的偏导数可依据式(9)得到。

当内、外方位元素均已知时，像点坐标改正数方程式可简化为：

如由3张像片p1，p2，p3按前方交会解法，求解未知点a在物方空间坐标系d-xyz内的空间坐标(x，y，z)，即可利用上述误差方程式进行解算，解算的原则是：要使点a的3个像点(a1，a2，a3)的像片坐标观测值的改正数的平方和为最小，即：

组成法方程，解得近似值(x0，y0，z0)的改正值(δx，δy，δz)，即可获得未知数坐标下一次的趋近值(x，y，z)：

由迭代判据确定迭代次数，迭代判据一般是可能获取精度的下一位的1，每一次仅解求一个待定点的三维空间坐标。