一种利用自平衡理论的板梁检测装置的制作方法

本实用新型涉及桥梁工程技术领域，具体涉及一种利用自平衡理论的板梁检测装置。

背景技术：

为保证钢筋混凝土桥梁质量，通常需要对单片预制梁进行现场试验检测。受工地试验条件的限制，对单根板梁，现场试验往往需要吊车、加载配重、加载支架(钢梁)、千斤顶、钢丝绳等，现场装配起来比较繁琐，非常不方便，使检测过程变得麻烦、效率低下，且带有一定的安全隐患，因而研制一种简洁方便的加载方式是十分必要的。

技术实现要素：

针对现有技术的不足，本实用新型提供了一种利用自平衡理论的板梁检测装置。

本实用新型将平面张弦梁的理论应用到梁的力学性能检测上，使梁的整个检测体系变成自平衡体系，把撑杆代替为千斤顶，在加载时，不需要外用大型起吊机器吊重物，只需要选取合适的拉钢索，控制千斤顶的伸长即可实现对梁的受力，使加载过程简单方便。

一种利用自平衡理论的板梁检测装置，包括：

试验梁；

安装在所述试验梁上的工字钢；

直立在所述工字钢上的千斤顶；

安装在所述千斤顶顶面的钢板；

连接在所述试验梁和钢板上的钢丝索。

本实用新型中，钢丝索将此体系变成自平衡体系，不需要外用大型起吊机器吊重物给千斤顶提供反力，而是利用钢丝索的抗拉张力约束千斤顶的伸长；钢丝索对梁的施加的力使此体系不再是简单的梁跨中受压结构，梁在受到跨中位置的集中力的同时，还受到钢丝索对梁端部的集中力，这个力可以分解为两部分，对梁的竖直方向的力与水平方向的力。水平方向的力等效为作用在梁轴线上的水平力，和作用在梁端部的弯矩，这个弯矩会对梁的跨中弯矩与挠度产生影响。

所述的工字钢为三个，其中，二个工字钢平行放置在所述试验梁上，另一工字钢放置在所述二个平行的工字钢上。

放置在所述二个平行的工字钢上的工字钢的长度方向与所述二个平行的工字钢的长度方向垂直。

所述的试验梁的两端设置有钩环，所述的钩环为半圆环结构。

所述的钢板的两端设置有两个安装孔。

所述的钢丝索的一端钩在所述钩环上，所述的钢丝索的另一端钩在所述钢板的安装孔上。

一种利用自平衡理论的板梁检测装置的梁力学检测方法，包括以下步骤：

1)根据千斤顶、工字钢与试验梁的尺寸及所需要施加的最大弯矩计算出所需钢索的面积as；

2)、根据试验梁跨中所对应的最大弯矩计算出千斤顶所需要加载的最大力fq1与对应的挠度；

3)根据计算得到的试验梁跨中总挠度y1、试验梁跨中上端应力σ上和试验梁跨中下端应力σ下评估实际质量。

步骤1)中，所需钢索的面积as计算具体包括：

a)选用的钢索弹性模量为es，θ0为未加载力时，钢索与梁的夹角，梁未受力时钢板到梁上钩环之间竖直位移为lx0，梁的长度l，eb为梁的弹性模量，ib为梁的截面系数，ab为梁的截面面积，m1为梁跨中所对应的最大弯矩；

b)计算所需钢索的长度ls0与所需钢索的面积as；

所需钢索的长度

所需钢索的面积的as的计算方式

如下：lx1为受力后钢板到梁上钩环之间竖直位移，为计算钢索总面积，需要人为确定一个lx1的最大伸长率λmax，其值在0到0.1之间，使千斤顶加载时，lx1,max的最大值lx1,max＝(1+λmax)lx0。as的计算公式为：

其中，h为试验梁的截面高度，a1为单根钢索的截面面积，表示向上取整数。

步骤2)中，根据试验梁跨中所对应的最大弯矩计算出千斤顶所需要加载的最大力fq1与对应的挠度，具体包括；

lx1的表达式为

δ1＝c²-3bd+12aeδ2＝2c³-9bcd+27ad²+27b²e-72ace

其中：

a＝4t²l²b＝4t²l²h-32m1tlc＝h²t²l²-16m1tlh+64m1²+t²l⁴-4t²l²ls0²

d＝-4ht²l²ls0²+ht²l⁴-8m1tl³

t为

试验梁跨中总挠度y1：

试验梁跨中上端应力σ上和试验梁跨中下端应力σ下分别为：

与现有技术相比，本实用新型的有益效果是：

本实用新型装置是利用自平衡体系的概念，实现对梁的力学性能检测。常规的梁的力学性能检测，是利用千斤顶对梁跨中施压，测试跨中的最大挠度和应力，加载过程需要吊车、加载配重、加载支架(钢梁)等，现场检测极不方便。本装置与传统工艺相比，采用钢索与梁的连接，使整个结构成为一个自平衡结构，利用钢索的约束，采用千斤顶加载，不需要大型器械，使本方法的检测变得方便。采用本实用新型装置检测得到的梁质量的目标参数(梁跨中总挠度y1、梁跨中上端应力σ上和梁跨中下端应力σ下)准确度高，并且简单快速，有利益于市场化推广利用。

附图说明

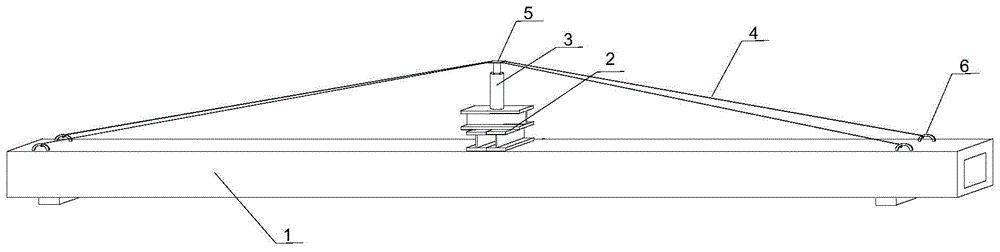
图1为本实用新型中利用自平衡理论的板梁检测装置的结构示意图；

图2为试验梁的截面图；

图3为钢丝索与试验梁的连接的结构示意图；

图4为钢丝索与钢板的连接的结构示意图；

图中：1-试验梁，2-工字钢，3-千斤顶，4-钢丝索，5-钢板，6-钩环预埋件。

具体实施方式

以下结合附图和实施实例对实用新型做进一步说明。

如图1所示，一种利用自平衡理论的板梁检测装置，包括：试验梁1，安装在试验梁1上并垫在千斤顶下的三个工字钢2，三个工字钢2中两个平行放置在试验梁1上，另一工字钢放置在二个平行的工字钢上，直立在工字钢2上的千斤顶3，连接千斤顶3与试验梁1的钢丝索4，钢丝索4直接用钩子勾在试验梁1的钩环预埋件6(钩环预埋件6形成环状结构，形成半圆环结构钩环，方便钢丝索4直接用钩子勾)上，一块两边带孔的钢板5放在千斤顶3上，钢丝索4直接勾在带孔钢板上。钢丝索4将此体系变成自平衡体系，不需要外用大型起吊机器吊重物给千斤顶3提供反力，直接利用钢丝索4的抗拉张力约束千斤顶3的伸长；钢丝索4对试验梁1的施加的力使此体系不再是简单的试验梁1跨中受压结构，试验梁1在受到跨中位置的集中力的同时，还受到钢丝索4对试验梁1的集中力，这个力可以分解为两部分，对试验梁1的竖直方向的力与水平方向的力，水平方向的力等效为作用在梁轴线上的水平力，和作用在梁端部的弯矩，这个弯矩会对梁的跨中弯矩与挠度产生影响。

如图2所示，为试验梁1的横截面，从试验梁1的横截面可知，试验梁1中部呈中空结构。

如图1、图2、图3所示，用钢丝索4分别勾住钢板5孔与试验梁1钩环预埋件6，形成自平衡体系，利用钢丝索4的抗拉刚度约束千斤顶的伸长。钢丝索4直接勾在试验梁1的钩环预埋件6上，一块两边带孔的钢板5放在千斤顶3上，钢丝索4直接勾在带孔钢板5上。

钢丝索4的最小根数可以根据千斤顶3、工字钢2与试验梁1的尺寸及所需要施加的最大弯矩计算出来。

一种利用自平衡理论的板梁检测装置的梁力学检测方法，包括以下步骤：

1)根据千斤顶3、工字钢2与试验梁1的尺寸及所需要施加的最大弯矩计算出所需钢索的面积as；

步骤1)中，所需钢索的面积as计算具体包括：

a)选用的钢索弹性模量为es，θ0为钢索与梁的夹角，梁1未受力时钢板到梁1上钩环之间竖直位移为lx0，梁1的长度l，eb为梁1的弹性模量，ib为梁1的截面系数，ab为梁1的截面面积，m1为梁1跨中所对应的最大弯矩；

b)计算所需钢索(即钢丝索4)的长度ls0与所需钢索的面积as，

所需钢索的面积的as的计算方式如下：lx1为受力后钢板到梁上钩环之间竖直位移，为计算钢索总面积，需要人为确定一个lx1的最大伸长率λmax，其值在0到0.1之间，使千斤顶加载时，lx1,max的最大值lx1,max＝(1+λmax)lx0。

as的计算公式为：

其中，h为试验梁的截面高度，a1为单根钢索的截面面积，表示向上取整数；

2)、根据试验梁跨中所对应的最大弯矩计算出千斤顶所需要加载的最大力fq1与对应的挠度；

lx1的表达式为

δ1＝c²-3bd+12aeδ2＝2c³-9bcd+27ad²+27b²e-72ace

其中：

a＝4t²l²b＝4t²l²h-32m1tlc＝h²t²l²-16m1tlh+64m1²+t²l⁴-4t²l²ls02

d＝-4ht²l²ls0²+ht²l⁴-8m1tl³

t为

试验梁1跨中总挠度y1：

试验梁1跨中上端应力σ上和试验梁跨中下端应力σ下分别为：

3)根据计算得到的试验梁1跨中总挠度y1、试验梁1跨中上端应力σ上和试验梁1跨中下端应力σ下评估实际质量。

本实施例为一根长为13m的梁横截面如图2，梁的弹性模量为3.45×10¹⁰pa，求最大弯矩360kn·m时，梁1在相应千斤顶3作用下的挠度。使用长0.34m的千斤顶，12.6a的工字钢，摆放方式见图1所示，lx0＝0.126+0.126+0.34-0.02＝0.572m，(0.02是因为索与梁连接处并不是在梁上，而是固定在梁上的钢筋上，为了计算的精确性，需要减掉)。索原长ls0为6.525m，索的弹性模量es为1.15×10⁵mpa，直径为6cm。a1＝2.83×10^-3m²。假设λmax＝0.0874<0.1。

计算钢索的根数，利用公式：

选取合适数量的钢索，由于选取的钢索面积大于所需的面积，所以千斤顶的伸长率一定小于0.1。

为了进一步佐证范例的正确性，用abauqs进行计算分析，基于abauqs的二维有限元分析如下：

abauqs的模型与理论计算模型类似，钢索简化为一根，面积为5.66×10^-3m²，其余数据都与理论分析部分一样。钢索为只受拉不受压的truss结构，试验梁为beam结构。

由于钢索作用在试验梁1的上部，而不是中轴线上，在试验梁1两端分别刚接两个钢臂，钢臂与千斤顶3的刚度是试验梁的100倍，并固定千斤顶3的转角，对千斤顶3底部跟试验梁跨中两点施加两个大小相同方向相反的力f。

利用上述公式计算的理论跨中挠度和abauqs模拟的下部挠度见表1，理论跨中弯矩、梁轴力和abauqs模拟的跨中弯矩、梁轴力见表2，理论跨中上下应力值和abauqs模拟的跨中上下应力值见表3，并附上abauqs值与理论计算的相对误差百分比。

表1理论跨中挠度和abauqs模拟的下部挠度对比表

表2理论跨中弯矩、梁轴力和abauqs模拟的跨中弯矩、梁轴力对比表

表3理论跨中上下应力值和abauqs模拟的跨中上下应力值对比表

通过算例可以证明，本专利研究的公式计算结果与abauqs模拟的计算结果相对误差都在3％以内。说明本专利的方法和公式简洁有效。

上面结合实施例对本实用新型的实施方法作了详细说明，但是本实用新型并不限于上述实施例，在本领域普通技术人员所具备的知识范围内，还可以在不脱离本实用新型宗旨的前提下作出各种变化。本实用新型说明书中未作详细描述的内容均可以采用现有技术。