一种时空分布不规则不均匀卫星高度计测高数据网格化处理方法与流程

本发明涉及卫星高度计测高数据处理技术领域，具体涉及以一种时空分布不规则不均匀的卫星高度计测高数据网格化处理方法，用于将时空观测不规则的hy-2系列卫星高度计沿轨测高数据处理为时空规则的网格数据。

背景技术：

卫星雷达高度计是一种通过发射雷达微波脉冲并接收其海面回波信号进行海洋观测的微波传感器。雷达高度计通过微波脉冲从卫星到海表面路径的时间延迟来计算卫星到海表面的距离，基于微波回波信号波形与后向散射特征提取海浪有效波高和海面风速。基于卫星雷达高度计的测量的卫星到海面的距离，结合卫星高度计轨道高度和各种距离校正值，计算得到海面相对于地球参考椭球的高度，即海面高度数据，也就是卫星高度计测高数据。卫星雷达高度计仅能获取卫星星下轨迹上的海面特征信息，其沿轨观测空间分辨率约为7km，卫星轨道间距与其重访周期有关，一般为几十公里到数百公里，因此卫星雷达高度计海面观测具有时空分布不均不规则的特点。

hy-2系列卫星是我国的海洋动力环境系列卫星，该系列卫星集主被动微波遥感器于一体，具有全天候、全天时和全球探测能力。2011年8月16日，我国发射了第一颗海洋动力环境卫星——hy-2a卫星。hy-2a卫星采用太阳同步轨道，倾角99.34°，降交点地方时为6:00am。雷达高度计是hy-2a卫星的主要载荷之一。hy-2a雷达高度计是一个双频雷达高度计，分别工作在ku波段(13.58ghz)和c波段(5.25ghz)。为了满足雷达高度计海洋观测需求，卫星在寿命前期采用重复周期为14天的回归冻结轨道，轨道高度为971km，每圈运行周期为104.46min，每天运行13+11/14圈；在寿命后期采用重复周期为168天的回归轨道，卫星轨道高度为973km，每圈运行周期为104.50min，每天运行13+131/168圈，主要用于大地测量学的研究。2018年10月25日，我国发射了第二颗海洋动力环境卫星——hy-2b卫星，其上同样搭载了与hy-2a卫星一致的雷达高度计。

卫星雷达高度计观测得到的海面高度数据，可用于海洋中尺度涡、大洋环流、潮汐和海平面变化等的研究，同时可为海洋数值模式提供输入数据。用于海洋中尺度涡、大洋环流和海平面变化研究以及海洋数值模式输入数据的海面高度数据需是时空分布规则的网格数据，而卫星高度计的观测数据为时空不均匀不规则的数据。hy-2系列卫星高度计的测高数据是时空分布不规则不均匀的，因此需进行hy-2系列卫星高度计测高数据网格化处理。针对hy-2系列卫星雷达高度计海洋观测的时空不一致性，从海洋中尺度动力观测的时空尺度特征出发，发展基于沿轨数据的hy-2系列高度计测高数据网格化方法成为了hy-2系列卫星高度计数据海洋应用的重要研究方向之一。

技术实现要素：

为了解决hy-2系列卫星雷达高度计海洋观测的时空不一致性的问题，本发明克服现有技术存在的不足，提供了一种hy-2系列卫星高度计测高数据网格化处理的方法，该方法实现基于hy-2a和hy-2b卫星高度计沿轨测高数据的海面高度异常网格数据生成，并可应用于后续hy-2系列卫星高度计的数据处理。该方法的特点是针对经数据预处理与质量控制以及基于jason-3高度计数据的hy-2系列卫星高度计数据统一和轨道误差修正处理后的hy-2系列卫星沿轨测高数据，利用时空客观分析方法，构建hy-2系列卫星高度计测高数据网格化处理算法，该方法考虑了hy-2系列卫星不同高度计之间的数据差异，以国外主流卫星高度计jason-3测高数据为基准参考进行数据处理。

为了解决上述技术问题，本发明采用的技术方案为：一种时空分布不规则不均匀卫星高度计测高数据网格化处理方法，包括以下步骤：

s1、分别对待处理卫星高度计和jason-3卫星高度计数据进行预处理和质量控制；

s2、分别计算待处理卫星高度计和jason-3卫星高度计的沿轨海面高度异常数据；

s3、以jason-3高度计为参考对待处理的测高数据进行数据统一；

s4、以jason-3高度计为参考对待处理的测高数据进行轨道误差修正；

s5、通过时空客观分析方法对待处理卫星高度计的测高数据进行网格化处理。

所述步骤s1中，预处理和质量控制的具体方法为，首先基于卫星高度计的数据编辑准则，去除受陆地、海冰、降雨等影响的数据，筛选出卫星测高值、干对流层校正值、湿对流层校正值、电离层校正值、海况偏差校正值、海洋潮汐、固体地球潮、极潮、有效波高观测值、后向散射系数观测值、海面风速值在数据编辑准则所要求范围内的数据，然后针对筛选后的数据计算沿轨海面高度观测值ssh；计算公式为：

ssh＝alt-(range+rangecorrected)-tide；

其中，alt为卫星轨道高度，range为高度计测量的卫星到海面的距离，rangecorrected是对高度计测量距离的校正值，tide为各种潮汐校正值的总和；

rangecorrected＝hdry+hwet+hiono+hssb+hib+hhf；

tide＝tset+tpt+tot+tlt；

其中，rangecorrected是对高度计测量距离的校正值，tide为各种潮汐校正值的总和；hdry为干对流层校正，hwet为湿对流层校正，hiono为电离层校正，hssb为海况偏差校正，hib为大气逆压校正，hhf为海面高频振荡校正，tset为固体地球潮，tpt为极潮，tot为海洋潮，tlt为负荷潮。

所述步骤s2中，沿轨海面高度异常数据的计算公式为：

sla＝ssh-mss；

其中，sla表示计算得到的沿轨海面高度异常数据，ssh为高度计沿轨海面高度；mss为对应于高度计观测点的平均海面高度，由平均海平面模型mss_cnes_2015的网格数据经线性插值计算得到该观测点的mss值。

所述步骤s3中，采用四参数模型对测高数据进行数据统一，其模型公式为：

式中，hobj为转换到目标框架即jason-3卫星参考框架的沿轨海面高度异常数据；horiginal为转化前的待处理卫星高度计的沿轨海面高度异常数据，λ、为对应观测点的经纬度，原点的三个空间偏移量δx、δy、δz和整体偏移量b为待求的四个参数；

数据统一时，将待处理卫星高度计与jason-3卫星高度计之间的互交叉点作为公共观测点，利用最小二乘法计算出所述四个参数，然后通过模型公式将待处理卫星高度计测高数据统一到jason-3测高数据的参考框架。

所述步骤s4中，进行轨道误差修正的具体方法为：

将待处理卫星高度计自身升降轨道的自交叉点相邻点处的sla值进行线性插值，分别得到自交叉点处待处理卫星高度计升轨和降轨的sla值，将二者的差记为自交叉点sla不符值；将待处理卫星高度计与jason-3高度计的轨道上与互交叉点相邻点处的sla值进行线性插值，分别得到互交叉点处待处理卫星高度计与jason-3高度计的sla值，将二者的差记为互交叉点处sla不符值；将自交叉点处的sla不符值的一半作为自交叉点处的轨道误差，互交叉点处的sla不符值记为互交叉点处的轨道误差，分别采用时间上连续的平滑三次样条函数进行拟合得到待处理卫星高度计的轨道误差，并用其对待处理卫星高度计的测量数据进行轨道误差校正，得到经轨道误差修正后的待处理卫星高度计沿轨sla数据。

所述的一种时空分布不规则不均匀卫星高度计测高数据网格化处理方法，还包括确定待处理卫星高度计与jason-3卫星高度计的轨道之间的互交叉点位置和待处理卫星高度计的卫星升轨和降轨轨道之间的自交叉点位置的步骤，其具体方法为：

将卫星绕地球一圈的轨道以其纬度最大值和最小值为界，分为升轨和降轨两种轨道，采用纬度与经度之间的二次多项式来拟合每一轨道，解算出拟合系数并建立轨道方程，联立两个轨道的方程组，计算交点位置经纬度，根据轨道首尾点经纬度判断两条轨道是否相交；若相交，取计算得到的交点位置的纬度作为参考纬度，在两个不同轨道上分别选取与参考纬度相邻的两个点，组成两条线段，两条线段相交或其延长线相交的交点即为交叉点的精确位置。

所述步骤s5中，对待处理卫星高度计的测高数据进行网格化处理的具体方法为：

s501、对步骤s4得到的沿轨海面高度异常数据进行低通滤波与重采样，得到预处理后的sla数据；

s502、根据给定的待估计的网格点(i,j)，通过时空尺度进行筛选，得到筛选后的sla数据；

s503、计算海面高度异常观测值自身的协方差矩阵a以及海面高度异常观测值与估计值之间的协方差矩阵c；

s504、计算得到网格点(i,j)的sla数据hij，计算公式为：

其中，表示观测值，cxj和aij分别表示海面高度异常观测值自身的协方差矩阵a的矩阵元以及海面高度异常观测值与估计值之间的协方差矩阵c的矩阵元。

所述步骤s501中，低通滤波采用lanczos低通滤波方法，重采样为采用每3选1的方法进行重采样。

所述步骤s504中，矩阵元aij和矩阵元cxj的计算公式分别：

其中，是观测点xi和xj之间的相关函数，是网格点x和观测点xi之间的相关函数，为网格点x处的海面高度异常值，<εiεj>表示误差方差。

本发明与现有技术相比具有以下有益效果：本发明提供了一种时空分布不规则不均匀卫星高度计测高数据的网格化处理方法，可以实现对hy-2a和hy-2b卫星高度计沿轨测高数据的网格化处理，生成空间分辨率为0.25°×0.25°的每天的全球海洋海面高度异常网格数据，最终实现将hy-2系列卫星高度计测高数据用于海洋中尺度涡、大洋环流、海平面变化等科学研究和海洋数值业务化预报的输入数据。

附图说明

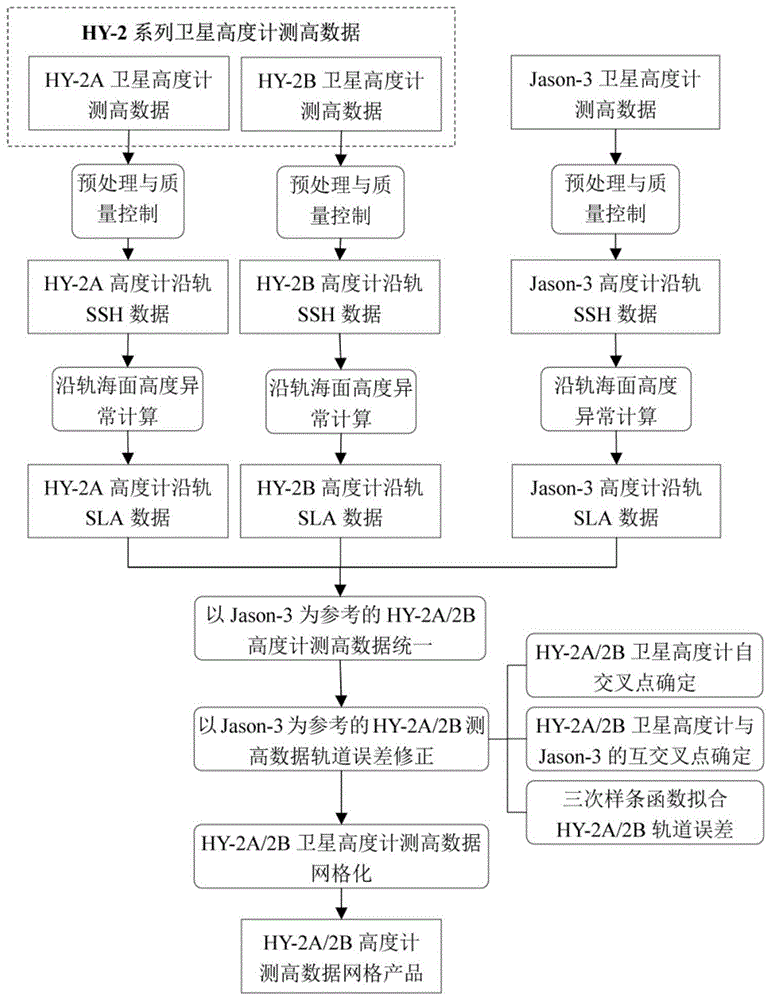
图1为本发明提出的一种hy-2系列卫星高度计测高数据的网格化处理方法的流程图；

图2为待处理卫星自交叉点及其与参考卫星互交叉点确定示意图；

图3为本发明实施例中的时空客观分析方法的具体流程图。

具体实施方式

为使本发明的技术方案和优点更加清楚，下面将结合具体实施例和附图，对本发明的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明的一部分实施例，而不是全部的实施例；基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明实施例提供了一种时空分布不规则不均匀卫星高度计测高数据网格化处理方法，其可以应用于对hy-2a/2b卫星高度计数据进行网格化处理，其具体包括以下几个步骤：

s1、分别对待处理卫星高度计和jason-3卫星高度计数据进行预处理和质量控制；

s2、分别计算待处理卫星高度计和jason-3卫星高度计的沿轨海面高度异常数据；

s3、以jason-3高度计为参考对待处理的测高数据进行数据统一；

s4、以jason-3高度计为参考对待处理的测高数据进行轨道误差修正；

s5、通过时空客观分析方法对待处理卫星高度计的测高数据进行网格化处理。

如图1所示，下面以hy-2系列卫星为例，详细说明本发明实施例的数据处理方法的具体步骤。

1.hy-2系列卫星高度计数据预处理与质量控制

预处理与质量控制的目的是基于卫星高度计自身的数据编辑准则，筛选过滤掉不满足数据质量要求的数据，然后针对筛选后的数据计算沿轨海面高度(seasurfacehight，ssh)观测值。针对hy-2a/2b雷达高度计数据和jason-3等卫星高度计gdr数据，利用各自数据手册中提供的数据编辑准则进行数据质量控制，包括去除受陆地、海冰、降雨等影响的数据，筛选出卫星测高值、干对流层校正值、湿对流层校正值、电离层校正值、海况偏差校正值、海洋潮汐、固体地球潮、极潮、有效波高观测值、后向散射系数观测值、海面风速值在数据编辑准则所要求范围内的数据，在此基础上计算出质量控制后hy-2a/2b和jason-3等卫星高度计的沿轨海面高度数据。

根据hy-2a、hy-2b和jason-3等高度计各自gdr数据中所包含的卫星轨道高度、测量距离、干对流层校正、湿对流层校正、电离层校正、海况偏差校正、大气逆压校正、海面高频振荡校正以及固体地球潮、极潮和海洋潮等潮汐校正，利用如下公式分别计算hy-2a、hy-2b和jason-3高度计的海面高度观测值：

ssh＝alt-(range+rangecorrected)-tide；(1)

rangecorrected＝hdry+hwet+hiono+hssb+hib+hhf；(2)

tide＝tset+tpt+tot+tlt；(3)

其中，alt为卫星轨道高度，range为高度计测量的卫星到海面的距离，rangecorrected是对高度计测量距离的校正值，tide为各种潮汐校正值的总和。hdry为干对流层校正，hwet为湿对流层校正，hiono为电离层校正，hssb为海况偏差校正，hib为大气逆压校正，hhf为海面高频振荡校正，tset为固体地球潮，tpt为极潮，tot为海洋潮，tlt为负荷潮。

2.hy-2系列卫星高度计沿轨海面高度异常(sealevelanomaly,sla)计算

海面高度异常(sla)是海表面相对于平均海平面的差值，它等于海面高度ssh与平均海平面高度mss(meanseasurface)的差。平均海平面mss一般为多年平均的海表面高度值，它的值由平均海平面模型得到。针对hy-2a/2b和jason-3卫星高度计测高数据，利用如下公式计算高度计沿轨sla值：

sla＝ssh-mss；(4)

其中，ssh为高度计沿轨海面高度；mss为对应于高度计观测点的平均海面高度，由平均海平面模型mss_cnes_2015的网格数据经线性插值计算得到该沿轨观测点的mss值。

3.以jason-3高度计为参考的hy-2a/2b卫星高度计测高数据统一

为了便于hy-2a/2b卫星高度计测高网格数据与国外同类数据的联合使用，在hy-2a/2b卫星高度计测高数据网格化时，将以jason-3高度计数据为参考进行hy-2a/2b卫星高度计测高数据统一。因hy-2a/2b卫星高度计和jason-3高度计的距离校正算法的差异使得不同测高卫星的海面高之间存在系统性差异，该差异通常采用四参数模型表示：

式中，hobj为转换到目标框架即jason-3卫星参考框架的sla；horiginal为待转换的hy-2a/2b卫星高度计sla，λ、为对应观测点的经纬度，待求的四个参数为原点的三个偏移量δx、δy、δz和整体偏移量b。分别将hy-2a/2b与jason-3高度计之间的互交叉点作为参考点，利用最小二乘法计算出参考框架转换的四个参数，计算出hy-2a/2b的转换参数，将hy-2a/2b卫星高度计测高数据统一到jason-3测高数据的参考框架。

4.以jason-3高度计为参考的hy-2a/2b卫星高度计测高数据轨道误差修正

以jason-3高度计测高数据为基准，根据hy-2a/2b卫星高度计的自交叉点和hy-2a/2b卫星高度计与jason-3高度计之间的互交叉点的sla不符值进行轨道误差修正，得到修正后的hy-2a/2b卫星高度计沿轨sla数据。该处理主要分为两步：一是确定出hy-2a/2b卫星高度计的自交叉点和hy-2a/2b卫星高度计与jason-3高度计的互交叉点位置，二是交叉点处sla偏差确定和基于偏差最小化计算轨道误差，最终进行hy-2a/2b卫星高度计sla数据的轨道误差修正。

(1)确定交叉点

卫星绕地球飞行的地面轨迹可分为上升和下降两种轨道，其中由南向北飞过赤道的轨迹称为上升轨道，由北向南飞过赤道的轨迹为下降轨道，同一卫星上升轨道与下降轨道之间交叉点称为自交叉点，不同卫星间轨道交叉点称为互交叉点，如图2所示，十字为待处理卫星轨道a，圆点是参考卫星轨道b，轨道a的升轨与降轨轨道之间的交叉点称为自交叉点，轨道a与轨道b之间的交叉点称为互交叉点。

将卫星绕地球一圈的轨道以其纬度最大值和最小值为界，分为升轨和降轨两种轨道，采用纬度与经度之间的二次多项式来拟合所有卫星(包括待处理卫星和参考卫星jason-3)的升轨轨道和降轨轨道，该二次多项式表示为：

式中，和λ分别为轨道点纬度和经度，a、b、c为轨道拟合系数。

根据(6)式解算出轨道拟合系数并建立轨道方程，联立两个轨道组成方程组，计算交点位置经纬度，再根据轨道首尾点经纬度判断两条轨道是否相交，若计算得到的交点经纬度位于两条轨道首尾点经纬度最小最大值之间，则轨道相交；若两条轨道相交，取交点位置的纬度作为参考纬度，在两个轨道上分别选取与参考纬度相邻的两个点，组成两条线段，两条线段相交或其延长线相交的交点即为交叉点的精确位置。

基于上述方法可以分别确定hy-2a/2b卫星高度计的自交叉点和hy-2a/2b卫星高度计与jason-3的互交叉点位置。

(2)轨道误差修正

确定交叉点位置后，需计算得到互交叉点和自交叉点处不同卫星轨道间的sla不符值，基于该sla不符值进行轨道误差修正。将两条不同轨道上与交叉点相邻点处的sla值进行线性插值，分别得到交叉点处不同轨道上的sla值，二者的差即为交叉点处sla不符值。对于自交叉点，取自交叉点不符值的一半为轨道误差；对于互交叉点，互交叉点sla的不符值为轨道误差。分别基于得到的自交叉点和互交叉点的轨道误差，采用时间上连续的平滑三次样条函数来拟合卫星高度计的轨道误差，并用于校正hy-2a/2b卫星高度计的轨道误差。利用计算得到的时间连续的轨道误差，分别对hy-2a/2b卫星高度计测高数据进行轨道误差校正，得到经轨道误差修正后的hy-2a/2b卫星高度计沿轨sla数据。

5.hy-2a/2b沿轨海面高度异常(sla)数据网格化处理

因高度计时空采样特点限制了海洋短尺度动力过程信号的正常提取，因此需开展hy-2a/2b高度计沿轨海面高度异常数据的沿轨低通滤波和重采样，以滤除海洋短尺度高频变化信息和随机测量误差，方便开展用于提取海洋中尺度变化过程信息的海面高度异常数据网格化处理。如图2所示，数据网格化处理的具体步骤如下。

(1)沿轨sla数据低通滤波与重采样

hy-2a/2b高度计沿轨sla数据低通滤波采用lanczos低通滤波方法，采用随纬度变化的截断波长，截断波长依据纬度分段选取，截断波长分别为250km(纬度<5°)、200km(5°≤纬度<10°)、150km(10°≤纬度<20°)、100km(20°≤纬度<30°)、75km(30°≤纬度<40°)和65km(纬度≥40°)。对于低通滤波后的hy-2a/2b卫星高度计沿轨sla数据采用每3选1的方法进行重采用。低通滤波和重采样后的hy-2a/2b高度计沿轨sla数据用于网格化处理。

(2)沿轨sla数据网格化

针对hy-2系列高度计沿轨观测数据的时空不规则性，采用时空客观分析法进行hy-2系列高度计海面高度观测数据网格化处理。该方法是将不同时刻观测获取的分布于不同空间位置的测高数据进行网格化处理的一种方法，方法具体流程如下。

设hij是待估计的网格点(i,j)处的海面高度异常网格数据，(i＝1,2,…,n)为高度计轨道位置处的海面高度异常观测值。基于时空尺度筛选出n个观测值，利用gauss-markov理论的最小二乘最优线性估计，则有：

其中，a是sla观测值自身的协方差矩阵，c是sla观测值与估计值之间的协方差矩阵。观测值可看作真实值hⁱ与观测误差εi之和，即：

协方差矩阵a和c分别为：

其中，是观测点xi和xj之间的相关函数，是网格点x和观测点xi之间的相关函数，为网格点x处的海面高度异常值，〈εiεj〉表示误差方差。

将高度计测量误差看作相关噪声，对于高度计每一周期测量数据，仅考虑沿轨的测量误差相关性，通过调整误差方差＜εiεj＞消除长波误差来实现，具体为：

其中，b²为测量白噪声的方差，δij为δ函数，elw为长波误差的方差，一般取为高度计信号方差的20％。

时空相关函数的表达式为：

式中，r为观测点与网格点之间或不同观测点之间的距离，t为观测时间差，a＝3.34/l，t表示时间相关尺度。具体地，r的表达式为：

式中，δx、δy和δt分别为观测点和待估计网格点的纬向、经向空间距离和时间间隔，lx、ly分别为空间纬向和经向相关尺度，cpx和cpy分别为对应经纬度区域多年平均纬向和经向传播速度。

其中，l表示空间相关尺度，lat为纬度。因此，根据上述公式中的时空尺度t、lx和ly可以筛选出满足时间条件和空间条件的观测数据。

综上所述，本发明提供了一种时空分布不规则不均匀卫星高度计测高数据的网格化处理方法，可以实现对hy-2a和hy-2b卫星高度计沿轨测高数据的网格化处理，生成空间分辨率为0.25°×0.25°的每天的全球海洋sla网格数据，最终实现将hy-2系列卫星高度计测高数据用于海洋中尺度涡、大洋环流、海平面变化等科学研究和海洋数值业务化预报的输入数据。

上面结合附图对本发明的实施例作了详细说明，但是本发明并不限于上述实施例，在本领域普通技术人员所具备的知识范围内，还可以在不脱离本发明宗旨的前提下作出各种变化。