引入抗差估计的因子图融合定位方法与流程

本发明涉及定位领域，具体地，涉及一种引入抗差估计的因子图融合定位方法。

背景技术：

随着智能交通与智能车辆的迅速发展，以及应用环境的复杂多变化，人们对运动目标状态信息估计的精确度也要求越来越高，单一的传感器已无法满足现有的导航需求，对各类导航源传感器的导航信息进行融合，实现传感器的优势互补，从而提高组合导航系统的精度、容错性和可靠性是重要的发展趋势。按照融合算法的结构，多源信息融合方法可大致分为三类：集中式融合方法、并行式融合方法和序贯式融合方法。其中，集中式融合方法在组合导航中，最成熟、应用最广泛的算法是kalman(卡尔曼)滤波，kalman滤波是一种最优估计，通常是在假定观测量是线性且符合高斯分布的情况下的最优估计。而在实际应用中，观测量却通常是非线性和非高斯的，因此出现了扩展卡尔曼滤波、无迹卡尔曼滤波和粒子滤波等非线性滤波方法。这些方法虽然解决了非线性、非高斯问题，但算法复杂度增加，导致融合效率降低。也有将神经网络引入到融合算法中对系统状态信息进行学习训练，但该方法需要大量训练样本且实时性较差；并行式融合方法中代表性的是carlson提出的联邦卡尔曼滤波算法，该算法是分散化的卡尔曼滤波算法，由多个子滤波器和一个主滤波器组成，通过主滤波器和各子滤波器的融合得到全局最优估计。该方法具有实时性好、计算量小的优点，但各滤波器输出量不一致，容易引入全局估计误差，且过度依赖观测信息，容错性差；序贯式融合方法是主要解决异步异构导航源信息的融合方法，有动静态滤波方法、交互自适应方法等，其中比较新颖的是20世纪90年代frkschischang等提出因子图方法，因子图是一种概率图模型，是将各导航源观测量信息进行编码，通过节点连接的方式将所有传感器观测因子搭建多源信息融合因子图框架，然后按照一定的规则进行消息传递和迭代，从而完成参数估计和数据融合。该方法可以融合非同频、非同步的传感器观测信息，其中各导航源信息是相互独立的，依次融合，向下传递，当增加或删除传感器时，只需要在因子图中添加或删除对应的结点，满足了系统即插即用的要求，但一旦某一导航源出现异常，不能及时识别，误差会向下累积，导致系统解算误差增大，从而造成定位精确度度低的问题。

技术实现要素：

本发明的目的在于，针对上述问题，提出一种引入抗差估计的因子图融合定位方法，以实现提高定位精确度的优点。

为实现上述目的，本发明实施例采用的技术方案是：

一种引入抗差估计的因子图融合定位方法，包括：

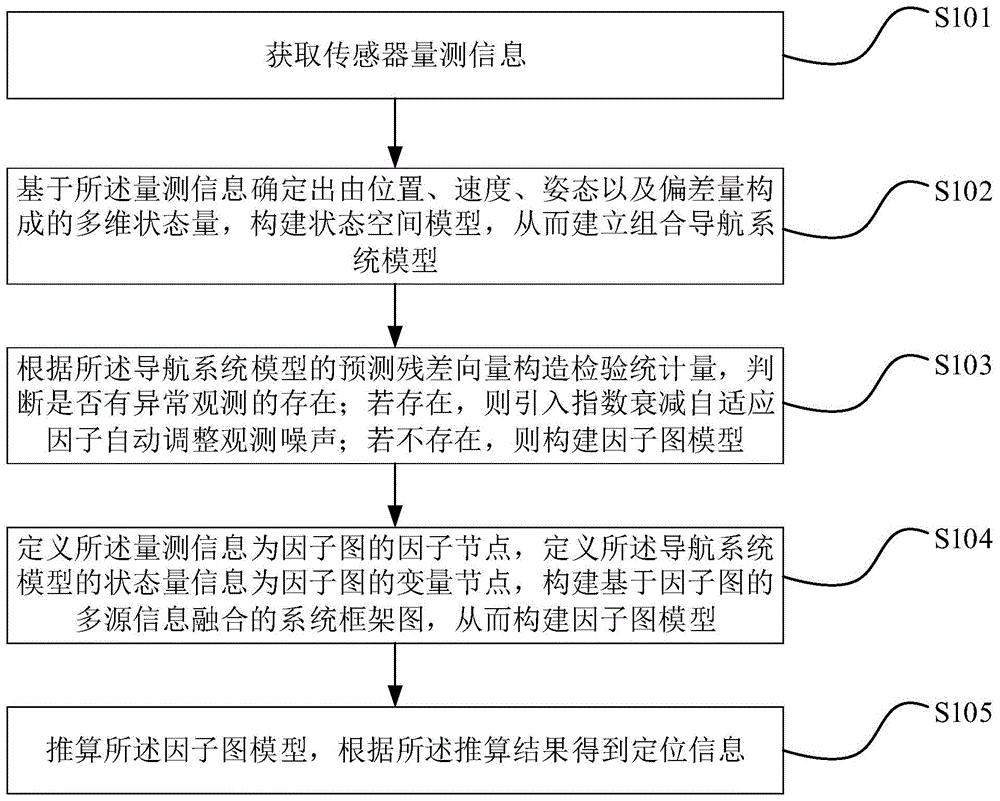
获取传感器量测信息；

基于所述量测信息确定出由位置、速度、姿态以及偏差量构成的多维状态量，构建状态空间模型，从而建立组合导航系统模型；

根据所述导航系统模型的预测残差向量构造检验统计量，判断是否有异常观测的存在；若存在，则引入指数衰减自适应因子自动调整观测噪声；若不存在，则构建因子图模型；

定义所述量测信息为因子图的因子节点，定义所述导航系统模型的状态量信息为因子图的变量节点，构建基于因子图的多源信息融合的系统框架图，从而构建因子图模型；

推算所述因子图模型，根据所述推算结果得到定位信息。

可选的，所述传感器量测信息，包括惯性测量单元中的陀螺仪和加速度计输出相应的角速度和比力的量测信息以及定位单元输出相应的经纬度量测信息。

可选的，所述状态空间模型为

式中，为k-1时刻的状态转移矩阵，hk为k时刻的观测矩阵；wk-1和vk分别为状态噪声和观测噪声，qk-1,rk为相应的协方差矩阵。

可选的，所述根据所述导航系统模型的预测残差向量构造检验统计量，判断是否有异常观测的存在为：

使用预测残差向量构造检验统计量，判断是否存在观测异常误差，从而判断是否有异常观测的存在。

可选的，所述使用预测残差向量构造检验统计量，判断是否存在观测异常误差，从而判断是否有异常观测的存在，包括：

设置置信度；

判断统计量是否超过置信度的极限，如超过置信度的极限，则存在观测异常误差。

可选的，所述置信度设置为：其中为显著性水平。

可选的，所述引入指数衰减自适应因子自动调整观测噪声，包括：

根据预测残差自动调整观测噪声，并设置噪声方差的上下限，当两个相邻的迭代差异未超过限制，则停止迭代。

可选的，定义所述量测信息为因子图的因子节点，定义所述导航系统模型的状态量信息为因子图的变量节点，构建基于因子图的多源信息融合的系统框架图，从而构建因子图模型为：

变量节点x，表示全局多元函数的变量，因子节点f，表示分解因子，变量节点x通过边e＝(eij)连接到因子节点f，边e＝(eij)是由变量节点x和因子节点f连线组成。

可选的，所述推算所述因子图模型，包括：

设置代价函数，将因子图模型消元变换为贝叶斯网络，通过高斯牛顿迭代法求解出状态更新量，最后得出最优估计值。

可选的，所述根据所述推算结果得到定位信息，包括：

基于最优估计值将获取的传感器量测信息进行融合，得到融合数据；

根据融合数据得到定位信息。

本发明的技术方案具有以下有益效果：

本发明技术方案，提出引入抗差估计的因子图融合方法，利用抗差估计对观测异常进行检测，并引入指数衰减自适应因子改变观测噪声协方差阵大小，从而抑制异常观测值的影响，提高融合算法的精度和容错性。达到提高定位精确度的目的。

下面通过附图和实施例，对本发明的技术方案做进一步的详细描述。

附图说明

图1为本发明实施例所述的引入抗差估计的因子图融合定位方法的流程图；

图2为本发明实施例所述的状态空间模型的因子示意图；

图3为本发明实施例所述的基于因子图的多源信息融合的系统框架图；

图4为本发明实施例所述的引入抗差估计的因子图融合方法的流程图。

具体实施方式

以下结合附图对本发明的优选实施例进行说明，应当理解，此处所描述的优选实施例仅用于说明和解释本发明，并不用于限定本发明。

如图1和图4所示，一种引入抗差估计的因子图融合定位方法，包括：

步骤s101：获取传感器量测信息；

可选的，所述传感器量测信息，包括惯性测量单元中的陀螺仪和加速度计输出相应的角速度和比力的量测信息，gps/bds/glonas/galileo单元输出相应的经纬度量测信息，其他各类辅助传感器输出对应的量测信息。

主要为imu惯性导航传感器、gps/bds/glonas/galileo卫星接收机、odo速度传感器等，imu传感器输出惯性测量单元中的陀螺仪和加速度计输出相应的角速度和比力的量测信息，gps/bds/glonas/galileo单元输出相应的经纬度量测信息，其他各类辅助传感器输出对应的量测信息。

步骤s102：基于所述量测信息确定出由位置、速度、姿态以及偏差量构成的多维状态量，构建状态空间模型，从而建立组合导航系统模型；

可选的，所述状态空间模型为

式中，为k-1时刻的状态转移矩阵，hk为k时刻的观测矩阵；wk-1和vk分别为状态噪声和观测噪声，qk-1,rk为相应的协方差矩阵。

对上式(1)的状态空间模型的因子图表示如图2所示；

以“东-北-天”坐标系为导航坐标系，选取状态变量x表示为：

式(2)中，φe,n,u为惯性平台东、北、天向的姿态失准角，δve,n,u为东、北、天向的速度误差，δl、δλ、δh分别表示纬度、经度、高度的误差，εx,y,z为陀螺仪的漂移误差，为加速度计的漂移误差。

对于组合导航系统，选取gps/bds/glonas/galileo单元与惯性导航系统的速度差和位置差作为观测向量，表示为：

zk＝[δveδvnδvu,δlδλδh](3)，

同样，其他传感器的量测方程可以写为：

式(4)中，h^others(.)为量测模型，n^others为观测噪声。添加其他传感器时在观测向量上添加相应的观测向量即可。

步骤s103：根据所述导航系统模型的预测残差向量构造检验统计量，判断是否有异常观测的存在；若存在，则引入指数衰减自适应因子自动调整观测噪声；若不存在，则构建因子图模型；

可选的，所述根据所述导航系统模型的预测残差向量构造检验统计量，判断是否有异常观测的存在为：

使用预测残差向量构造检验统计量，判断是否存在观测异常误差，从而判断是否有异常观测的存在。

可选的，所述使用预测残差向量构造检验统计量，判断是否存在观测异常误差，从而判断是否有异常观测的存在，包括：

设置置信度；

判断统计量是否超过置信度的极限，如超过置信度的极限，则存在观测异常误差。

可选的，所述置信度设置为：其中为显著性水平。

可选的，所述引入指数衰减自适应因子自动调整观测噪声，包括：

根据预测残差自动调整观测噪声，并设置噪声方差的上下限，当两个相邻的迭代差异未超过限制，则停止迭代。

引入抗差估计技术，首先是对异常观测信息进行检测，本发明利用预测残差向量构造检验统计量，从而判断是否存在观测异常误差。

预测残差(新息)表示k时刻的真实量测值zk与量测一步预测之间存在的误差，定义式为：

预测残差的均方误差阵为则

测量新息(预测残差)为白噪声序列，服从均值为零，方差的正态分布，即

将其归一化，得检验统计量为：

式(8)中，hki表示在时间k时刻的观测矩阵的第i行元素，rki表示观测噪声协方差矩阵的对角元素。

假设置信度为检验统计量不超过置信极限，则可以认为没有观测异常；如果超过置信极限，引入衰减自适应因子来调整观测噪声协方差矩阵，达到识别和抑制观测量异常影响的目的。

引入抗差估计的因子图融合方法，其特征在于，引入指数衰减自适应因子自动调整观测噪声。

通过式(6)可以得出预测残差的方差的表达式为：

预测残差的方差代表随机序列的集总平均，可以用离散化方程中的时间平均代替，对方程(9)进行移项，观测噪声协方差矩阵可改写为：

将上式(10)中用b(0<b<1)代替，令式(10)可以转化为：

考虑到观测异常误差可能会很大，通过式(11)计算噪声协方差时会增加异常观测的影响，令所以等式(11)可以表示为：

当引入指数衰减自适应因子更新滤波器时，可以根据预测残差自动调整观测噪声，并设置了噪声方差的上下限，避免矩阵逆为负时降低滤波精度。同时，如果两个相邻的迭代差异未超过限制，则停止迭代。

步骤s104：定义所述量测信息为因子图的因子节点，定义所述导航系统模型的状态量信息为因子图的变量节点，构建基于因子图的多源信息融合的系统框架图，从而构建因子图模型；

可选的，定义所述量测信息为因子图的因子节点，定义所述导航系统模型的状态量信息为因子图的变量节点，构建基于因子图的多源信息融合的系统框架图，从而构建因子图模型为：

变量节点x，表示全局多元函数的变量，因子节点f，表示分解因子，变量节点x通过边e＝(eij)连接到因子节点f，边e＝(eij)是由变量节点x和因子节点f连线组成。

构建因子图模型，因子图是一种表示随机变量联合概率分布的二分图模型，可以将多元变量的全局函数分解为多个局部函数因子的乘积。因子图模型包括两种节点，一种是变量节点x，表示全局多元函数的变量，一种是因子节点f，表示分解因子，变量节点通过边e连接到因子节点，所以因子图定义为：

g＝(f,x,e)(13)，

式(13)中，是变量节点的集合，m为变量节点的个数；f＝{f1(x1),f2(x2),...,fn(xn)}代表一组因子节点，n为变量节点的个数；边e＝(eij)是由变量节点和因子节点连线组成。

因子图定义了一个函数的分解式：

定义惯性测量单元以及其他辅助传感器输出的量测信息为因子图的因子节点，定义导航系统的状态量信息为因子图的变量节点，从而构建基于因子图的多源信息融合的系统框架图，如图3所示。图中，fothers为其他传感器辅助时引入的新的因子节点，因此，基于因子图的多源信息融合方法具有相当好的灵活性，可以实现传感器的即插即用。图3中●为因子节点，○为变量节点。

步骤s105：推算所述因子图模型，根据所述推算结果得到定位信息。

求解联合概率分布p(xk|zk)的最大后验估计，设置代价函数，将因子图模型消元变换为贝叶斯网络，通过高斯牛顿迭代法求解出状态更新量，最后得出最优估计值，完成多源信息的有效融合。

可选的，所述推算所述因子图模型，包括：

设置代价函数，将因子图模型消元变换为贝叶斯网络，通过高斯牛顿迭代法求解出状态更新量，最后得出最优估计值。

可选的，所述根据所述推算结果得到定位信息，包括：

基于最优估计值将获取的传感器量测信息进行融合，得到融合数据；

根据融合数据得到定位信息。

根据贝叶斯估计，联合概率密度p(xk|zk)可分解为：

且全局条件概率密度函数与分子中的似然概率密度和状态转换先验概率成正比：

根据最大后验估计准则，将具有最大后验概率密度的状态变量视为估计量。因此，因子图的推算实质上是求解联合概率分布p(xk|zk)的最大后验概率估计的过程，最大后验概率表达式为：

为了计算最大后验概率估计等式(16)的右侧p(zi|xi)p(xi|xi-1)将最大化。

对于高斯分布而言，p(zi|xi)可以表示为：

式(18)中，w为方差矩阵，hi()为量测函数，zi为实测值。

设置代价函数为：

j＝[zi-hi(xi)]^tw^-1[zi-hi(xi)]＝min(19)，

因此，令代价函数取最小值，求解最优估计量。对于线性量测量，可采用求极值法求解最优估计量对于非线性量测量，可采用牛顿迭代法进行求解。当在图中添加新的因子节点zk时，利用不同传感器的测量值计算最优解。

类似地，p(xi|xi-1)可以用同样的方法计算得到：

式(20)中，p为方差矩阵。

设置代价函数为：

令误差函数的代价函数取最小值，最优状态估计量即可得出，完成多源信息融合。

本发明实施例具有以下效果和优点：

1.采用的因子图融合方法，相比联邦滤波等其他多源信息融合方法，能够对异步异构的传感器数据进行处理，满足了系统中传感器的即插即用功能，提高了组合导航的灵活性。

2.引入抗差估计技术，能够检验系统异常观测量，并采用自适应因子调节观测噪声，提高了系统的导航精度和容错性。

3.解决了传统因子图方法中，如果某一导航源出现异常导致误差累积，系统导航解算误差增大的问题，同时降低了算法的计算复杂度。

最后应说明的是：以上所述仅为本发明的优选实施例而已，并不用于限制本发明，尽管参照前述实施例对本发明进行了详细的说明，对于本领域的技术人员来说，其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。