基于BP神经网络和主元分析法的齿轮箱故障诊断方法及系统与流程

本发明涉及齿轮箱故障诊断方法，具体涉及一种基于bp神经网络和主元分析法的齿轮箱故障诊断方法及系统。

背景技术：

齿轮箱是用来改变转速和传递动力的常用机械设备，由于齿轮箱本身工作环境恶劣，容易受到损害和出现故障。当齿轮箱发生机械故障时，总会出现噪声和振动等现象。想要通过振动信号来准确的识别故障类型，需要对振动信号进行有效的去噪处理，以排除噪声对故障特征的干扰和影响。

粒子滤波，即通过寻找一组在状态空间中传播的随机样本来近似的表示概率密度函数，用样本均值代替积分运算，进而获得系统状态的最小方差估计的过程，这些样本被形象的称为“粒子”。粒子滤波算法是一种处理非线性信号的有效算法，该算法在故障诊断、导航定位、无限通讯等诸多领域应用广泛，是当今国内外研究的热点。

但是，粒子滤波算法易于陷入局部极值的缺陷，识别率和精度低，对于不同的齿轮箱，普适性不高。

技术实现要素：

本发明的目的是提供一种基于bp神经网络和主元分析法的齿轮箱故障诊断方法及系统，本发明将bp神经网络与主元分析和粒子滤波相结合，能广泛应用于不同类型的齿轮箱故障诊断，且具有较高识别率和精度，普适性高。

本发明所采用的技术方案是：

一种基于bp神经网络和主元分析法的齿轮箱故障诊断方法，包括步骤：

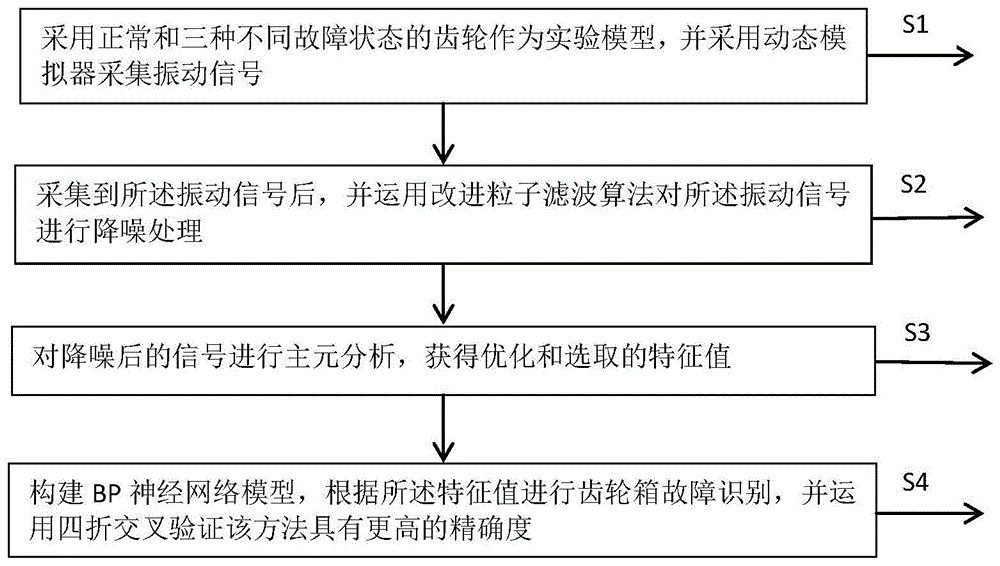
步骤1、采用正常和若干种不同故障状态的齿轮作为实验模型，采集振动信号；

步骤2、运用改进的粒子滤波算法对采集的振动信号进行降噪处理；改进的粒子滤波算法是将遗传变异算法和粒子群优化算法结合并引入到粒子滤波算法的采样过程中；

步骤3、对降噪后的振动信号进行主元分析，获得优化和选取的特征值；

步骤4、构建bp神经网络模型，根据获得的特征值进行齿轮箱故障识别，并运用四折交叉验证精确度。

在步骤1中，振动信号通过加速度传感器和动态模拟器采集；采集前，根据正常和若干种不同故障状态的齿轮的参数信息分别确定加速度传感器的参数和动态模拟器的参数。

进一步地，正常和若干种不同故障状态的齿轮的参数信息包括齿轮的尺寸、裂纹角度和微裂纹的位置，加速度传感器的参数包括安装位置和工作参数，动态模拟器的参数包括安装位置和采集参数设置。

在步骤2中，改进的粒子滤波算法包括步骤：

步骤21、初始化；

步骤22、优化粒子集样本分析；

步骤23、计算重要性权值；

步骤24、重采样；

步骤25、输出。

在步骤21中，初始化包括在k＝0时刻，根据p(x0)分布采样得到即初始化群体数目n，学习因子c1和c2，惯性系数ω，初始粒子的位置xi和速度vi，最大迭代次数epochmax，预设变异率m。

在步骤22中，优化粒子集样本分析包括步骤：

步骤22.1、按式y(epoch)＝(1-(epoch/epochmax)^α)^β计算控制函数y(epoch)，epoch为迭代次数，α和β为变异控制系数；

步骤22.2、按式ω＝ωmin+(ωmax-ωmin)·y(epoch)计算惯性系数ω，ωmin和ωmax分别为最小惯性系数和最大惯性系数；

步骤22.3、根据式u＝m·y(epoch)计算变异率u，根据式m＝[n*u]计算变异粒子数m，按式xkj＝xkj+rand*y(epoch)进行变异操作；

步骤22.4、对于每个粒子，按式计算适应度值fit[i]，并与其个体最优值pi进行比较iffit[i]＞pithenpi＝fit[i]，求解全局最优值gi，即ifpi＞githengi＝pi；

步骤22.5、根据式更新粒子的速度vi和位置xi；当达到最大迭代次数或者粒子群的最优值符合某阈值ε时，则输出结果即可得到新的粒子样本

在步骤23中，计算重要性权值包括：

采样重要性权值的计算公式为权值归一化计算公式为

在步骤24中，重采样包括：

根据重要性权值从集合中重新采样得到k时刻的新粒子集合根据得到新的粒子权值。

在步骤25中，输出包括：

输出状态估计样本集状态估计计算公式为

在步骤3中，对降噪后的振动信号进行主元分析，获得优化和选取的特征值，包括步骤：

步骤31、计算样本均值：

步骤32、求解样本向量协方差矩阵计算s的特征值λ1，λ2，…，λn以及其对应的特征向量ν1，v2，…，νn；

步骤33、计算各主元的贡献率和累计贡献率选取前p个累计贡献率满足要求的主元作为映射矩阵，将原始信号变换到特征空间：y＝v^txk，其中v＝(v1，ν2，…，νp)，计算改进的粒子滤波算法去噪处理后的主元贡献率和累计贡献率。

在步骤4中，包括步骤：

使用sigmoid函数为传递函数，bp神经网络结构的输入层节点数n＝4，输出层节点数m＝4，隐含层节点数目m由公式确定；

将经过改进的粒子滤波算法降噪后再经主元分析优化后的样本数据随机分作4份，带入构建的bp神经网络模型中进行齿轮故障诊断，并进行四折交叉验证该方法的高精确度；

四折交叉验证时，将数据分成四份，一份用来测试，剩下三份用来训练神经网络，验证精度为每次验证准确率的平均值。训练时，只改变神经元隐层节点数目m的大小，将训练样本输入建立的网络模拟空间进行训练。

一种基于上述bp神经网络和主元分析法的齿轮箱故障诊断方法的齿轮箱故障诊断系统，包括信号采集单元、滤波单元、主元分析单元和bp神经网络单元；信号采集单元采用动态模拟器在齿轮箱上采集振动信号；滤波单元用于采用改进的粒子滤波算法对采集的振动信号进行滤波处理；主元分析单元用于对滤波后的振动信号进行主元分析，获得优化和选择的特征值；bp神经网络单元用于对优化和选择的特征值进行故障识别。

本发明的有益效果是：

本发明将bp神经网络与主元分析和粒子滤波相结合，能广泛应用于不同类型的齿轮箱故障诊断，且具有较高识别率和精度，普适性高——本发明将带变异算子的粒子群优化算法引入到粒子滤波的采样过程中构成改进的粒子滤波算法，有效的避免了算法的粒子贫乏和采样后期样本单一的问题，提高了收敛速度和精度，并用该算法对正常和三种不同故障齿轮进行测试取得振动信号进行降噪处理，对进行降噪后的信号进行主元分析，降低振动信号数据的维度和相关性，降低了神经网络训练和测试的负担，构建bp神经网络模型对提取特征值进行故障诊断，并用四折交叉验证模型诊断精度进行评估和验证。通过仿真实验和设置的齿轮箱故障实验证明了该去噪算法的有效性，结果表明该方法对齿轮箱故障诊断具有更高的精确度，能广泛应用于不同齿轮箱故障诊断，普适性高。

附图说明

图1为本发明实施例的诊断方法的流程示意图。

图2为本发明实施例的齿轮箱结构示意图。

图3为本发明实施例的齿轮箱信号采集系统示意图。

图4为本发明实施例的一改进的粒子滤波算法流程图。

具体实施方式

以下结合附图对本发明进行描述，所举实例只用于解释本发明，并非用于限定本发明的范围。

一种基于bp神经网络和主元分析法的齿轮箱故障诊断方法，包括步骤：

步骤1、采用正常和若干种不同故障状态的齿轮作为实验模型，采集振动信号；在本实施例中，正常状态f1表示齿轮无裂纹，三种故障状态f2、f3、f4表示有裂纹的齿轮，其中f2、f3、f4分别表示裂纹全深度和全宽度的1/4、1/2、3/4，齿轮裂纹全深度a＝2.4mm，裂纹全宽度b＝25mm，裂纹的厚度为0.4mm，齿轮裂纹的角度为45°，实验中齿轮箱为空载状态，转速为800r/min，分别用s1、s2、s3和s4表示正常情况与三种不同故障情况下的情况。

步骤2、运用改进的粒子滤波算法对采集的振动信号进行降噪处理；改进的粒子滤波算法是将遗传变异算法和粒子群优化算法结合并引入到粒子滤波算法的采样过程中。

步骤3、对降噪后的振动信号进行主元分析(主元分析法，目前基于多元统计过程控制的故障诊断技术的核心，是基于原始数据空间，通过构造一组新的潜隐变量来降低原始数据空间的维数，再从新的映射空间抽取主要变化信息，提取统计特征，从而构成对原始数据空间特性的理解)，获得优化和选取的特征值。

步骤4、构建bp神经网络模型(bp神经网络，一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络)，根据获得的特征值进行齿轮箱故障识别，并运用四折交叉验证精确度。

在步骤1中，振动信号通过加速度传感器和动态模拟器采集；采集前，根据正常和若干种不同故障状态的齿轮的参数信息分别确定加速度传感器的参数和动态模拟器的参数。

正常和若干种不同故障状态的齿轮的参数信息包括齿轮的尺寸、裂纹角度和微裂纹的位置，加速度传感器的参数包括安装位置和工作参数，动态模拟器的参数包括安装位置和采集参数设置。在本实施例中，将两个pcb352c67型加速度传感器分别安装在齿轮箱的水平和垂直方向上，采用spectraquest型动态模拟器来采集齿轮箱振动信号。通过dsp20-42型频谱分析仪，将得到的振动信号输入到电脑中并储存。对安装在水平方向上的传感器所测得的振动信号进行分析。

在步骤2中，改进的粒子滤波算法包括步骤：

步骤21、初始化；

步骤22、优化粒子集样本分析；

步骤23、计算重要性权值；

步骤24、重采样；

步骤25、输出。

在步骤21中，初始化包括在k＝0时刻，根据p(x0)分布采样得到即初始化群体数目n，学习因子c1和c2，惯性系数ω，初始粒子的位置xi和速度vi，最大迭代次数epochmax，预设变异率m。

在步骤22中，优化粒子集样本分析包括步骤：

步骤22.1、按式y(epoch)＝(1-(epoch/epochmax)^α)^β计算控制函数y(epoch)，epoch为迭代次数，α和β为变异控制系数；

步骤22.2、按式ω＝ωmin+(ωmax-ωmin)·y(epoch)计算惯性系数ω，ωmin和ωmax分别为最小惯性系数和最大惯性系数；

步骤22.3、根据式u＝m·y(epoch)计算变异率u，根据式m＝[n*u]计算变异粒子数m，按式xkj＝xkj+rand*y(epoch)进行变异操作；

步骤22.4、对于每个粒子，按式计算适应度值fit[i]，并与其个体最优值pi进行比较iffit[i]＞pithenpi＝fit[i]，求解全局最优值gi，即ifpi＞githengi＝pi；

步骤22.5、根据式更新粒子的速度vi和位置xi；当达到最大迭代次数或者粒子群的最优值符合某阈值ε时，则输出结果即可得到新的粒子样本

在步骤23中，计算重要性权值包括：

采样重要性权值的计算公式为权值归一化计算公式为

在步骤24中，重采样包括：

根据重要性权值从集合中重新采样得到k时刻的新粒子集合根据得到新的粒子权值。

在步骤25中，输出包括：

输出状态估计样本集状态估计计算公式为

在本实施例中，选取的原始信号方程：

加入随机噪音信号后得加噪信号z(t)＝y(t)+0.005r(t)。初始概率密度函数为n(0，2)，状态初始值为1，观测噪声方差r＝1×10^-4，过程噪声方差q＝1×10^-5。粒子个数n＝30，适应度阈值ε＝0.001，最大迭代数epochmax＝200，变异控制系数α和β分别为1.7和10，ωmax和ωmin分别为0.7298和0.1，加速度常数c1和c2分别为1.4692。分别对n＝100，n＝500，n＝1000三种粒子数目进行实验仿真。

在步骤3中，对降噪后的振动信号进行主元分析，获得优化和选取的特征值，包括步骤：

步骤31、计算样本均值：

步骤32、求解样本向量协方差矩阵计算s的特征值λ1，λ2，…，λn以及其对应的特征向量ν1，v2，…，νn；

步骤33、计算各主元的贡献率和累计贡献率选取前p个累计贡献率满足要求的主元作为映射矩阵，将原始信号变换到特征空间：y＝v^txk，其中v＝(ν1，ν2，…，νp)，计算改进的粒子滤波算法去噪处理后的主元贡献率和累计贡献率。

在步骤4中，包括步骤：

使用sigmoid函数为传递函数，bp神经网络结构的输入层节点数n＝4，输出层节点数m＝4，隐含层节点数目m由公式确定；

将经过改进的粒子滤波算法降噪后再经主元分析优化后的样本数据随机分作4份(在本实施例中，共用样本160组)，带入构建的bp神经网络模型中进行齿轮故障诊断，并进行四折交叉验证该方法的高精确度；

四折交叉验证时，将数据分成四份，一份用来测试，剩下三份用来训练神经网络，验证精度为每次验证准确率的平均值。训练时，只改变神经元隐层节点数目m的大小，将训练样本输入建立的网络模拟空间进行训练。

一种基于上述bp神经网络和主元分析法的齿轮箱故障诊断方法的齿轮箱故障诊断系统，包括信号采集单元、滤波单元、主元分析单元和bp神经网络单元；信号采集单元采用动态模拟器在齿轮箱上采集振动信号；滤波单元用于采用改进的粒子滤波算法对采集的振动信号进行滤波处理；主元分析单元用于对滤波后的振动信号进行主元分析，获得优化和选择的特征值；bp神经网络单元用于对优化和选择的特征值进行故障识别。

本发明将bp神经网络与主元分析和粒子滤波相结合，能广泛应用于不同类型的齿轮箱故障诊断，且具有较高识别率和精度，普适性高——本发明将带变异算子的粒子群优化算法引入到粒子滤波的采样过程中构成改进的粒子滤波算法，有效的避免了算法的粒子贫乏和采样后期样本单一的问题，提高了收敛速度和精度，并用该算法对正常和三种不同故障齿轮进行测试取得振动信号进行降噪处理，对进行降噪后的信号进行主元分析，降低振动信号数据的维度和相关性，降低了神经网络训练和测试的负担，构建bp神经网络模型对提取特征值进行故障诊断，并用四折交叉验证模型诊断精度进行评估和验证。通过仿真实验和设置的齿轮箱故障实验证明了该去噪算法的有效性，结果表明该方法对齿轮箱故障诊断具有更高的精确度，能广泛应用于不同齿轮箱故障诊断，普适性高。