一种基于恒星拍摄的珞珈一号相机-星敏安装标定方法与流程
本发明涉及星载光学夜间灯光影像无控定位技术领域,具体涉及一种基于恒星拍摄的珞珈一号相机-星敏安装标定方法。
背景技术:
卫星在发射过程中释放的应力,卫星在在轨后物理环境的改变,都会致使相机-星敏夹角会发生变化,影响卫星影像的定位精度。故在卫星影像投入实际应用前,需要对相机-星敏夹角进行标定,以提高卫星影像定位精度。
目前,国内外已经开展了在轨几何定标研究,如在轨精确标定相机-星敏夹角的研究。此外,各国多采用利用地面高精度控制点的方式来进行相机-星敏夹角标定。但精度地面控制点的获取不仅耗费大量的人力物力,其质量也是影响卫星影像相机-星敏夹角标定的重要因素,因此克服对地面控制点的依赖,提出无需地面控制点的相机-星敏夹角标定方法具有重要的意义。
本申请发明人在实施本发明的过程中,发现现有技术的方法,至少存在如下技术问题:
相机-星敏夹角会随着季节光照变化等因素的影响而出现长周期的持续变化,致使单次定标无法真的保证卫星影像的无控定位精度。为保证卫星影像的无控定位精度,需要对在轨卫星开展长周期的高频次定标,但高精度控制点获取的频次、质量和数量等问题是影响该方法质量的关键因素。而对于像珞珈一号卫星等夜晚成像且敏捷机动性较差的卫星夜光影像,控制数据更为缺乏,难以通过传统方法实现高频次的定标,来提高卫星无控定位精度。
综上可知,现有技术中需要获取高精度地面控制点导致标定较为复杂的技术问题。
技术实现要素:
本发明提出一种基于恒星拍摄的珞珈一号相机-星敏安装标定方法,用于解决或者至少部分解决现有技术中需要获取高精度地面控制点导致的标定较为复杂的技术问题。
为了解决上述技术问题,本发明提供了一种基于恒星拍摄的珞珈一号相机-星敏安装标定方法,包括:
s1:从利用相机和星敏同时拍摄的星图中提取恒星星点的位置坐标;
s2:根据提取出的位置坐标,通过星图识别和修正得到恒星在j2000坐标系下的位置;
s3:根据恒星在j2000坐标系下的位置,求取星敏和相机分别在j2000坐标系下的姿态;
s4:根据星敏和相机分别在j2000坐标系下的姿态,对星敏-相机之间的夹角进行标定。
在一种实施方式中,s1包括:
s1.1:采用对拍摄时段获取的多帧星图进行累加求平均值的方法提取背景噪声,并去除背景噪声,设包含星点的卫星图像亮度值表示为f(x,y),则k景星图提取的背景噪声b(x,y)为:
s1.2:对步骤s1.1获取的去除背景噪声的星点影像,利用图像阈值分割方法,进行图形背景分割:设t为背景阈值,按照下式原始图像进行阈值分割,得到阈值化处理后的图像f(x,y),
s1.3:根据步骤1.2中阈值化处理后的图像中属于同一颗星点的像素,通过连通域标记可获得亮度初始位置信息和结束位置信息:(m1,n1),(m2,n2);
s1.4:利用灰度平方加权质心法对阈值化处理后的f(x,y)求一阶矩,求得第i颗恒星星点质心亚像元坐标(xi,yi):
在一种实施方式中,s2包括:
s2.1:利用栅格法对珞珈一号01星数据进行星图识别,在g×g大小的网格上进行二值化投影,并对网格元素赋值,网格中有星点的为1,没有星点的为0,生成的网格图像作为该星的模式向量;
s2.2:将观测星生成的模式向量psi与导航星模式库中的模式向量pci进行逻辑与运算,对运算生成的每颗恒星向量求和,当psi与pci一致时,则运算结果为1,否则为0,将g×g范围内所有的运算结果进行统计,最大一致的图像模式所对应的恒星作为识别结果:
s2.3:对因恒星自行产生的位移进行修正,得到修正后的恒星位置。
在一种实施方式中,对因恒星自行产生的位移进行修正,得到修正后的恒星位置,包括:通过下述公式及计算修正后的恒星位置,
在一种实施方式中,s3包括:
s3.1:根据相机/星敏得到的观测星生成的模式向量psi与导航星模式库中的模式向量pci之间的对应关系,将第i颗恒星在瞬时j2000坐标系下的测量向量表示为:
s3.2:通过坐标系间的转换,第i颗恒星在星图上的坐标为(xi,yi),转换到相机/星敏坐标系下的测量向量为:
s3.3:在相机/星敏在j2000坐标系下处于某一姿态矩阵
在一种实施方式中,在步骤s3.3之后,所述方法还包括:
s3.4:通过最小二乘准则,寻找相机坐标系到j2000坐标系,或者星敏坐标系到j2000坐标系最优姿态矩阵:
s3.5:根据s3.4中的最优姿态矩阵以及预设算法,得到姿态四元数为:
在一种实施方式中,在步骤s3.5之后,所述方法还包括:采用光行差修正方法对姿态四元数进行修正,
s3.6:获取光行差公式:
s3.7:利用地心惯性坐标系j2000、太阳质心参考系三个坐标轴的方向一致进行相加,得到卫星在太阳质心参考系下的速度vh:vh=vsc+ve,vsc表示卫星在j2000坐标系下的速度,ve表示地球在以太阳为质心,j2000坐标系下的速度;
s3.8:根据光行差公式和卫星在太阳质心参考系下的速度,计算获得光行差造成的偏差角度:
s3.9:根据偏差角度和旋转轴,采用轴/角公式构建四元数形式的变换关系,即光行差修正四元数δq为:
在一种实施方式中,s4包括:
s4.1:根据s3.3中获得的
其中
本申请实施例中的上述一个或多个技术方案,至少具有如下一种或多种技术效果:
本发明公开的一种基于恒星拍摄的珞珈一号相机-星敏安装标定方法,首先从利用相机和星敏同时拍摄的星图中提取恒星星点在星图中的位置坐标;然后根据提取出的位置坐标,通过星图识别和修正得到恒星在j2000坐标系下的位置;接着根据恒星在j2000坐标系下的位置,求取星敏和相机分别在j2000坐标系下的姿态;最后根据星敏和相机分别在j2000坐标系下的姿态,对星敏-相机之间的夹角进行标定。可以不需要地面控制点,即可以实现星敏-相机之间的标定,标定效率高。
附图说明
为了更清楚地说明本发明实施例或现有技术中的技术方案,下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍,显而易见地,下面描述中的附图是本发明的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动的前提下,还可以根据这些附图获得其他的附图。
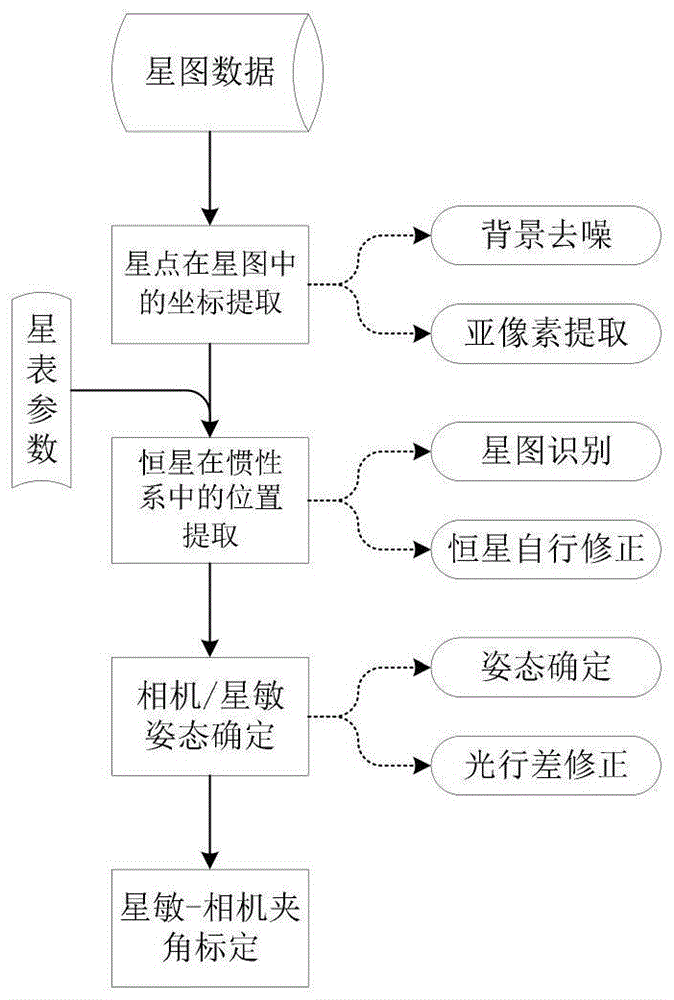
图1为本发明提供的珞珈一号相机-星敏标定流程图;
图2为本发明采用的相机/星敏恒星观测原理图;
图3为本发明实施例中光行差示意图。
具体实施方式
针对现有技术存在的不足,本发明针对珞珈一号01星夜光卫星的相机-星敏在轨定标,提出了无需地面控制点的标定方法,该方法利用相机、星敏同时对恒星曝光拍摄,通过对相机、星敏获取的星图进行处理来精确标定相机-星敏夹角本发明主要构思如下:
步骤1:利用相机和星敏同时拍摄的星图提取恒星星点的坐标;步骤2,恒星在j2000坐标系中的位置的提取;步骤3,星敏和相机在各自的惯性系下的姿态确定;步骤4,利用最小二乘法标定星敏-相机之间的夹角。
本发明顾及高精度地面控制点难以获取以及较难实现高频次相机-星敏夹角的标定的发展现状,提出了无需地面控制点的相机-星敏夹角标定方法,并以珞珈一号01星真实在轨数据为基础进行实验证明该方法的有效性,保证了珞珈一号01星无控地面定位精度。
为使本发明实施例的目的、技术方案和优点更加清楚,下面将结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚、完整地描述,显然,所描述的实施例是本发明一部分实施例,而不是全部的实施例。基于本发明中的实施例,本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例,都属于本发明保护的范围。
本实施例提供了一种基于恒星拍摄的珞珈一号相机-星敏安装标定方法,请参见图1,该方法包括:
s1:从利用相机和星敏同时拍摄的星图中提取恒星星点的位置坐标;
s2:根据提取出的位置坐标,通过星图识别和修正得到恒星在j2000坐标系下的位置;
s3:根据恒星在j2000坐标系下的位置,求取星敏和相机分别在j2000坐标系下的姿态;
s4:根据星敏和相机分别在j2000坐标系下的姿态,对星敏-相机之间的夹角进行标定。
具体来说,s1中,利用相机和星敏同时对恒星曝光拍摄,从拍摄得到的星图(星数据)中提取出恒星星点的位置坐标。
在一种实施方式中,s1包括:
s1.1:采用对拍摄时段获取的多帧星图进行累加求平均值的方法提取背景噪声,并去除背景噪声,设包含星点的卫星图像亮度值表示为f(x,y),则k景星图提取的背景噪声b(x,y)为:
s1.2:对步骤s1.1获取的去除背景噪声的星点影像,利用图像阈值分割方法,进行图形背景分割:设t为背景阈值,按照下式原始图像进行阈值分割,得到阈值化处理后的图像f(x,y),
s1.3:根据步骤1.2中阈值化处理后的图像中属于同一颗星点的像素,通过连通域标记可获得亮度初始位置信息和结束位置信息:(m1,n1),(m2,n2);
s1.4:利用灰度平方加权质心法对阈值化处理后的f(x,y)求一阶矩,求得第i颗恒星星点质心亚像元坐标(xi,yi):
具体来说,由于珞珈一号01星相机及星敏拍摄的星图具有较强背景噪声,因此,采用对拍摄时段获取的多帧星图进行累加求平均值的方法来提取背景噪声。
亮度初始位置信息和结束位置信息:(m1,n1),(m2,n2)即为同一颗星点在连通域内开始和结束对应的坐标位置。
如附图2和附图3所示,表示恒星在j2000坐标系中的位置提取。图2中,stars1-stars3为恒星,f为焦距,o-xsyszs为小孔坐标系,o-xccdyccd为成像坐标系。
图3中,s为观测者静止时恒星位置,a为观测值运动时恒星位置,θ为运动方向和光源的夹角,v为观测者的运动速度,c为光速)
在一种实施方式中,s2包括:
s2.1:利用栅格法对珞珈一号01星数据进行星图识别,在g×g大小的网格上进行二值化投影,并对网格元素赋值,网格中有星点的为1,没有星点的为0,生成的网格图像作为该星的模式向量;
s2.2:将观测星生成的模式向量psi与导航星模式库中的模式向量pci进行逻辑与运算,对运算生成的每颗恒星向量求和,当psi与pci一致时,则运算结果为1,否则为0,将g×g范围内所有的运算结果进行统计,最大一致的图像模式所对应的恒星作为识别结果:
s2.3:对因恒星自行产生的位移进行修正,得到修正后的恒星位置。
具体来说,s2.2中观测星生成的模式向量为s2.1中的模式向量。由于在宇宙中,每一颗恒星都按照自己的运行规律相对太阳系进行高速运动,因此,需要对因恒星自行产生的位移要进行计算改正。
在一种实施方式中,对因恒星自行产生的位移进行修正,得到修正后的恒星位置,包括:通过下述公式及计算修正后的恒星位置,
具体来说,假定在短时间内恒星自行视为常数,根据t'年内自行对恒星赤经赤纬位置的影响,可以计算出修正后的恒星位置,即每颗恒星在瞬时j2000坐标系下的赤经赤纬。
在一种实施方式中,s3包括:
s3.1:根据相机/星敏得到的观测星生成的模式向量psi与导航星模式库中的模式向量pci之间的对应关系,将第i颗恒星在瞬时j2000坐标系下的测量向量表示为:
s3.2:通过坐标系间的转换,第i颗恒星在星图上的坐标为(xi,yi),转换到相机/星敏坐标系下的测量向量为:
s3.3:在相机/星敏在j2000坐标系下处于某一姿态矩阵
具体来说,s3.1~3.3位姿态确定的方法:根据小孔成像的原理,相机/星敏得到的观测星生成的模式向量psi与导航星模式库中的模式向量pci存在一一对应的关系,从而可以得到第i颗恒星在瞬时j2000坐标系下的测量向量表示,然后通过坐标系转换,得到相机/星敏坐标系下的测量向量。triad算法为双矢量定姿算法,通过两颗恒星确定姿态矩阵
在一种实施方式中,在步骤s3.3之后,所述方法还包括:
s3.4:通过最小二乘准则,寻找相机坐标系到j2000坐标系,或者星敏坐标系到j2000坐标系最优姿态矩阵:
s3.5:根据s3.4中的最优姿态矩阵以及预设算法,得到姿态四元数为:
具体来说,由于相机/星敏视场内会识别出多颗恒星,导致多颗恒星建立了冗余观测,本发明通过最小二乘准则,寻找到相机坐标系到j2000坐标系,或者星敏坐标系到j2000坐标系最优姿态矩阵,姿态四元数即为寻找到的最优姿态矩阵。预设算法可以为q-method(davenport’sqmethod)、quest(quaternionestimator)、svd(singularvaluedecomposition)、foam(fastoptimalattitudematrix)、esoq(estimatoroftheoptimalquaternion)等算法。
在一种实施方式中,在步骤s3.5之后,所述方法还包括:采用光行差修正方法对姿态四元数进行修正,
s3.6:获取光行差公式:
s3.7:利用地心惯性坐标系j2000、太阳质心参考系三个坐标轴的方向一致进行相加,得到卫星在太阳质心参考系下的速度vh:vh=vsc+ve,vsc表示卫星在j2000坐标系下的速度,ve表示地球在以太阳为质心,j2000坐标系下的速度;
s3.8:根据光行差公式和卫星在太阳质心参考系下的速度,计算获得光行差造成的偏差角度:
s3.9:根据偏差角度和旋转轴,采用轴/角公式构建四元数形式的变换关系,即光行差修正四元数δq为:
具体来说,本发明还对最优姿态矩阵采用光行差的方式进行修正。太阳质心参考系三个坐标轴包括:ox、oy和oz轴,ox位于赤道平面内,指向特定历元时刻的太阳春分点;oy轴位于赤道平面内,与ox垂直、oz轴指向历元时刻地球北极的平均位置。
在一种实施方式中,s4包括:
s4.1:根据s3.3中获得的
其中
与现有技术相比,本发明具有如下优点和有益效果:
(1)本发明提出的相机-星敏夹角标定方法,无需地面控制点,可提高标定效率,节约大量的人力物力。
(2)本发明顾及高精度地面控制点难以获取以及较难实现高频次相机-星敏夹角的标定的发展现状提出的无需地面控制点的相机-星敏夹角标定方法保证夜间灯光影像无控定位精度。
以上所述的具体描述,对发明的目的、技术方案和有益效果进行了进一步详细说明,所应理解的是,以上所述仅为本发明的具体实施例而已,并不用于限定本发明的保护范围,凡在本发明的精神和原则之内,所做的任何修改、等同替换、改进等,均应包含在本发明的保护范围之内。
- 还没有人留言评论。精彩留言会获得点赞!