一种基于统计约束的叠后密度反演方法与流程

本发明涉及油气勘探技术领域，具体为一种基于统计约束的叠后密度反演方法。

背景技术：

在地球物理勘探领域，密度是表征储层的一个固有属性，密度可用于判别岩性，分析矿物的成分，若矿物成分和流体密度已知，可直接计算孔隙度，用于储层的评价。所以，地下介质的密度是地球物理探测的重要参数之一。

储层预测的核心是地震反演，以叠后地震资料为基础资料的储层反演方法是储层预测的重要方法，在进行叠后地震属性分析与反演的时候，一般只能关注振幅与纵波速度或者一个参数之间的关系。叠后地震数据反演未能给出泊松比、纵横波速度比等反应物性、流体特征的参数，限制了储层物性、流体特征的研究。随着勘探开发难度的不断加大，使用叠后地震储层预测技术来完成岩性地层油气勘探的任务越来越困难。

目前，从地震数据中获取密度参数的主要方法是利用avo反演，avo反演的理论基础是zoeppritz方程及其近似式。使用avo近似式进行三参数反演的时候，经常会出现反演中纵波速度基本较为准确，但是横波速度与密度的准确性较差。由于小偏移距的振幅数据主要受控于地震纵波速度，对密度参数敏感的是中远偏移距振幅，用avo反演获取密度参数需要大偏移距地震数据，一般来说，超过常规地震孔径的大偏移距数据资料品质差、信噪比低、动校拉伸严重，各向异性明显，因此，只利用偏移距变化的振幅数据的avo密度反演的难度较大。avo反演方法的分辨率较高，相对较为成熟，但是反演不确定性较高，结果无法准确预测，反演参数不够可靠，反演效果不理想。

技术实现要素：

本发明的目的在于提供一种基于统计约束的叠后密度反演方法，以解决上述背景技术中提出的问题。

为了解决上述技术问题，本发明提供如下技术方案：

一种基于统计约束的叠后密度反演方法，包括以下步骤：

步骤一：利用统计回归方法获得井上纵波vp、密度ρ数据统计回归系数，密度与纵波的统计回归关系：ρ＝avp^b，a、b是统计回归关系系数，利用最小二乘方法计算得到a＝a，b＝b；

步骤二：建立以密度与纵波统计关系为正则约束的目标函数，如下公式：

公式：l＝(wr-d)^t(wr-d)+λ(ρ-avp^b)^t(ρ-avp^b)(2-1)

公式：

上述公式(2－1)中的a，b是步骤一中的统计回归关系系数a、b；w是子波矩阵，r是反射系数；

步骤三、采用迭代优化算法反演纵波vp、密度ρ：

求解目标函数公式(2－1)，得目标函数的解为：

公式：

其中m＝[vp,ρ]，g＝w[jacobivp,jacobiρ]，c＝[ace^b,ce]，ce是密度反演变化量归一化的方差矩阵，λ是正则约束条件的系数，d是叠后地震观测数据，d＝wr，w是子波矩阵，r是反射系数；

公式：

公式：

公式：

公式：

公式：

公式：

雅各比jacobi矩阵是反射系数r关于纵波、密度的偏导矩阵，公式(3－2)到公式(3－7)是具体计算雅各比jacobi矩阵，叠后地震观测数据长度是n，其中上标“—”指上界面，上标“+”指下界面；

利用人工合成数据说明算法的运算过程为：

步骤301：算法输入数据，所述算法输入数据包括叠后地震观测数据、纵波模型、密度模型及井上纵波与密度的统计回归关系系数a、b；

步骤302：求纵波与密度的初始值与子波褶积的正演结果与叠后地震观测数据的差值△d＝d-wr0；

步骤303：根据公式(3－2)至公式(3－7)计算反射系数对纵波与密度的雅各比矩阵，用g＝w[jacobivp,jacobiρ]组合纵波与密度的雅各比矩阵间接得到地震关于纵波与密度的变化率，结合纵波与密度的统计回归关系系数a、b，代入公式(3－1)，求解出正演与叠后地震观测数据的差值对应的纵波与密度的变化量△vp和△ρ；

步骤304：更新反演纵波、密度结果：vp＝vp0+△vp，ρ＝ρ0+△ρ；

步骤305：将步骤304中得到的纵波、密度反演结果代入公式(2－2)与褶积模型d＝wr正演合成新的叠后地震观测数据；

步骤306：判断正演地震数据与叠后地震观测数据之间的累积误差如果满足设定量级，则停止迭代扰动，反演结束，输出结果；如果正演地震数据与叠后地震观测数据之间的累积误差未达到设定量级，则遍历步骤302－步骤305继续迭代扰动。

上述中，所述步骤301中，所述叠后地震数据是利用纵波速度和密度用公式(2－2)计算反射系数，与子波褶积合成叠后地震观测数据d。

上述中，所述步骤301中，所述纵波模型及所述密度模型，分别采用井上纵波与密度的低频部分，作为迭代算法扰动的初始值。

上述中，所述步骤301中，所述井上纵波与密度满足指数型统计回归关系，其系数是a、b，利用最小二乘方法计算得到a＝a，b＝b。

与现有技术相比，本发明所达到的有益效果是：本方法采用逐步迭代方法求解，首先将纵波模型与密度模型作为反演的初始模型，计算褶积正演记录与叠后地震观测数据d之间的误差，用公式(3－1)计算纵波与密度的变化量，更新纵波、密度反演结果，若褶积正演记录与叠后地震观测数据之间的误差足够小时，停止迭代扰动，反演过程结束。

本发明区别于传统的叠前道集avo密度反演受制于反演准确性与参数贡献度的制约，本发明利用了叠后地震观测数据进行密度反演，叠后地震观测数据资料相对于叠前道集资料其信噪比高很多，可以直接进行反演而无需进行过多的预处理工作。本发明采用的纵波、密度二维同时反演，以纵波与密度之间的统计关系为正则约束条件，平衡了参数量级不同对观测数据的贡献度，以褶积模型为基础，当纵波与密度的回归相关度较低时，仍然能得到比较可靠的密度反演结果。

附图说明

附图用来提供对本发明的进一步理解，并且构成说明书的一部分，与本发明的实施例一起用于解释本发明，并不构成对本发明的限制。在附图中：

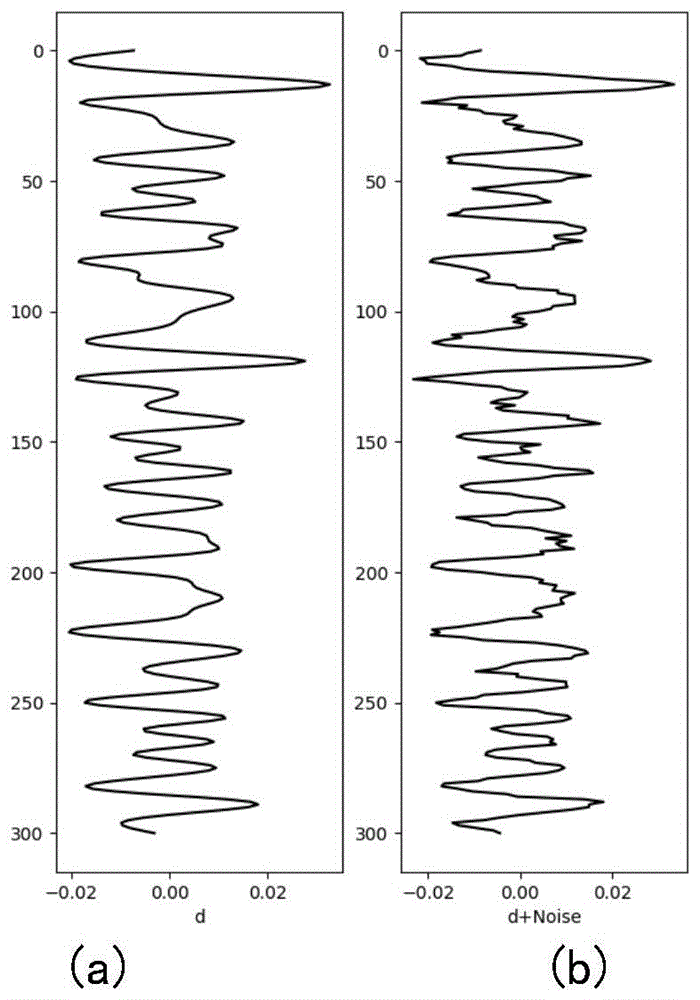
图1为本发明实施例中试验数据之一示意图，其中图1(a)为理论合成记录；图1(b)为理论合成记录加噪声。

图2为本发明实施例中试验数据纵波vp与密度ρ的交会图。

图3为本发明实施例中子波试验数据之一。

图4为本发明实施例中试验数据之二，其中图4(a)是纵波模型；图4(b)是密度模型。

图5为本发明实施例中试验反演结果，其中图5(a)为纵波反演对比，图5(b)为密度反演对比。

图6为本发明方法的算法流程图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明提出了一种基于统计约束的叠后密度反演方法，该方法采用信噪比相对较高的叠后地震观测数据，以褶积模型为基础，采用逐步迭代方式，获取全局最优的密度反演结果。具体步骤如下：

步骤一：利用统计回归方法获得井上纵波、密度数据统计回归系数；

步骤二：建立密度与纵波统计关系为正则约束的目标函数；

步骤三：采用迭代优化算法反演纵波、密度。

所述具体步骤为：

步骤一、利用统计回归方法获得井上纵波vp、密度ρ数据统计回归系数：密度与纵波之间符合指数型统计回归关系：ρ＝avp^b。

使用井上实测纵波(声波时差的倒数)和密度进行最小二乘回归计算，得到统计回归关系系数a＝a、b＝b。

步骤二、建立密度ρ与纵波vp统计关系为约束的目标函数，如下公式：

公式：l＝(wr-d)^t(wr-d)+λ(ρ-avp^b)^t(ρ-avp^b)(2-1)

公式：

上述公式(2－1)中a，b是由井上统计回归得到的vp与ρ之间统计回归关系系数，w是子波矩阵，r是反射系数。在目标函数中加入纵波与密度的回归关系是为了平衡纵波与密度数量级和对叠后地震观测数据的贡献度，有利用优化反演目标求取。

步骤三、采用迭代优化算法反演纵波vp、密度ρ：

求解目标函数公式(2－1)，得目标函数的解为：

公式：

其中m＝[vp,ρ]，g＝w[jacobivp,jacobiρ]，c＝[ace^b,ce]，ce是密度反演变化量归一化的方差矩阵，λ是正则约束条件的系数，d是叠后地震观测数据，d＝wr，w是子波矩阵，r是反射系数。

雅各比jacobi矩阵是反射系数r关于纵波、密度的偏导矩阵，公式(3－2)到公式(3－7)是具体计算雅各比jacobi矩阵，叠后地震观测数据长度是n，其中上标“—”指上界面，上标“+”指下界面。

根据图6的算法设计流程图所示：利用人工合成数据说明算法的运算过程：包括算法输入数据及算法迭代反演过程。所述算法输入数据包括：叠后地震记录，纵波模型，密度模型，井上纵波与密度的统计回归关系系数a、b。所述算法迭代反演过程包括：(1)求纵波与密度的初始值与附图3所示的子波褶积的正演结果与叠后地震观测数据图1(b)的差值△d＝d-wr0；(2)根据公式(3－2)至公式(3－7)计算反射系数对纵波与密度的雅各比矩阵，用g＝w[jacobivp,jacobiρ]组合纵波与密度的雅各比矩阵间接得到叠后地震观测数据关于纵波与密度的变化率，结合井上纵波与密度的统计关系参数(a、b)，代入(3－1)式，求解出正演与叠后地震观测数据的差值对应的纵波与密度的变化量△vp和△ρ；(3)更新反演纵波、密度结果：vp＝vp0+△vp，ρ＝ρ0+△ρ；(4)将(3)得到的纵波、密度反演结果代入公式(2－2)与褶积模型d＝wr正演合成新的叠后地震观测数据，正演地震数据与叠后地震观测数据的之间的累积误差如果足够小或满足设定量级，则停止迭代扰动，反演结束，输出结果，图5是反演结果与准确值的对比；若累积误差未达到满意量级，则遍历(1)～(4)继续迭代扰动。

叠后地震观测数据：利用纵波速度和密度用公式(2－2)计算反射系数，与子波褶积合成叠后地震观测数据d如图1(a)所示，为了试验算法的鲁棒性，对叠后地震观测数据添加随机噪声，如图1(b)所示。纵波模型与密度模型：分别采用井上纵波与密度如图5(a)、图5(b)的实线的低频部分，其中图5(a)为纵波反演对比，实线是准确纵波速度，虚线是反演纵波；图5(b)为密度反演对比，实线是准确密度，虚线是反演密度。

作为迭代算法扰动的初始值，如图4所示。井上纵波与密度的统计关系系数：利用最小二乘方法计算得到统计回归关系系数a、b，图2是井上纵波与密度的交会图。

本方法采用逐步迭代方法求解，首先将纵波模型与密度模型作为反演的初始模型，计算褶积正演记录与叠后地震观测数据d之间的误差，用公式(3－1)计算纵波与密度的变化量，更新纵波、密度反演结果，若褶积正演记录与观测数据之间的误差足够小时，停止迭代扰动，反演过程结束。

本发明区别于传统的叠前道集avo密度反演受制于反演准确性与参数贡献度的制约，本发明利用了叠后地震进行密度反演，叠后地震资料相对于叠前道集资料其信噪比高很多，可以直接进行反演而无需进行过多的预处理工作。本发明采用的纵波、密度二维同时反演，以纵波与密度之间的统计关系为正则约束条件，平衡了参数量级不同对观测数据的贡献度，以褶积模型为基础，可以得到比较可靠的密度反演结果。

最后应说明的是：以上所述仅为本发明的优选实施例而已，并不用于限制本发明，尽管参照前述实施例对本发明进行了详细的说明，对于本领域的技术人员来说，其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。