一种包装件缓冲性能的非破坏性测试方法与流程

本发明涉及一种包装件缓冲性能的非破坏性测试方法，属于包装测试方法技术领域及物流包装技术领域。

背景技术：

近年来，随着我国经济的快速发展，互联网和物联网技术的的加强，我国的物流业和电商经济也得到了前所未有的辉煌，电商物流包装作为保护商品、方便储运的主要技术手段越发显得重要。与此同时，快速发展的背后也带来了许多问题：

(1)由于国内物流环境条件的不完善和物流过程中包装不当引起的产品破损事件屡屡发生，造成了惨痛的经济损失。据数据统计，近五年来由于包装不当等因素造成的产品损失高达150亿元/年。

(2)随着电商需求量的日益扩大，也造成了大量的包装垃圾，加速了国内环境的恶化。

(3)伴随国内老龄化现象的加剧，人口红利带来的利润优势不再，导致国内许多企业急需压缩成本以保证生存。

基于上述问题，社会对包装提出了“质量优化、降低成本、绿色环保”的新要求，如何改进传统的包装件性能测试方法，促进包装设计逐渐满足新的要求，已成为包装和物流两大行业的重要研究发明。

对普通商品如日用品洗发水来说，用传统的实验室试验进行性能测试的成本大概在一千元左右。但对价格高的商品而言，传统测试方法的测试成本非常高。例如，耳熟能详的几款名牌手表：百达翡丽、江诗丹顿、朗格、宝珀等每一款的市价都在35万元以上，按照传统的测试方法，一般每件产品都至少需要3次测试，且每次都需更换新产品，则其测试成本将高达35×3＝105万元。而对于一些更高端的商品而言，其价格更高，高昂的测试成本对于普通企业将无法负担。为此，本发明基于此问题提出一种非破坏性的性能测试方法，从测试源头降低包装成本，为企业创造经济效益。

技术实现要素：

根据以上现有技术中的不足，本发明要解决的技术问题是：为解决上述问题之一，提供一种包装件缓冲性能的非破坏性测试方法，基于包装常用缓冲材料epe，针对其非线性力学模型，根据等效跌落数学模型，综合利用传统跌落试验和maplesim数值–符号仿真方法，提出非破坏性的包装性能测试方法，本专利的成功实施不仅可以降低测试成本、提高测试效率，还可以为缓冲包装性能测试提供新的思路和理论支持。

本发明为解决上述问题所采用的技术方案是：

为解决上述问题之一，提供一种包装件缓冲性能的非破坏性测试方法，其特征在于：包括如下步骤：

s1，首先利用包装件试验样品和冲击跌落试验机进行冲击跌落预试验，进行安全跌落高度的跌落测试并记录激励和响应脉冲值，然后进行目标跌落高度的跌落测试并记录激励脉冲；

s2，其次根据epe材料的非线性力学模型和等效跌落数学模型模型来进行仿真参数的理论计算和转换；

s3，接着进行maplesim仿真，通过安全跌落高度响应加速度值预测目标跌落高度响应加速度值。具体为：接着从搭建好的maplesim元件库中依次选择所需元件，对其属性和参数进行设置，依据模型图连接各元件和组件，建立包装件试验样品的仿真模型，进行maplesim仿真，通过安全跌落高度响应加速度值预测目标跌落高度响应加速度值。

优选地，所述步骤s1，具体包括如下步骤：

s11，根据设计要求确定目标和安全跌落高度；

s12，将产品在安全跌落高度下进行冲击跌落试验，记录输入和响应脉冲数据；

s13，在目标跌落高度下执行冲击跌落测试，获得目标跌落高度的输入脉冲。

所述步骤s2，具体包括如下步骤：

s21，根据实验数据计算模型参数：非线性弹簧初始刚度系数k0、非线性系数r、阻尼系数c。

所述步骤s3，具体包括如下步骤：

s31，在仿真软件中建立仿真模型；

s32，输入参数m、k0、r、c及目标跌落高度下的输入脉冲等数据至仿真模型中；

s33，运行仿真，记录仿真结果。

优选地，所述步骤s12，第一次跌落试验：第一次冲击跌落试验在安全跌落高度20cm下进行，测试数据用于参数的计算，具体步骤如下：

s121：确定安全跌落高度，将冲击台提升到此高度；

s122：将测试样品固定在冲击台上；

s123：同时释放样品和冲击台，记录实验数据(如输入加速度、响应加速度和冲击持续时间等)。

所述步骤s13，第二次跌落试验：第二次冲击跌落试验在目标跌落高度下进行，测试用于获得目标跌落高度的输入脉冲，具体步骤如下：

s131：确定目标跌落高度，将冲击台提升到此高度；

s132：释放冲击台，记录输入脉冲。

优选地，所述epe材料的非线性力学模型的建立步骤如下：首先对epe材料进行动态压缩试验，进而建立epe材料的非线性动力学模型，然后利用变分迭代法求解非线性动力学方程，最后进行试验验证，将变分迭代解与试验实测结果相比较，验证变分迭代法的准确性及新建立的模型的可行性。

优选地，所述等效跌落数学模型模型的建立步骤如下：首先以发泡类材料epe为研究对象，建立质量块–非线性弹簧模型的等效跌落数学模型，然后，在上述模型基础上建立质量块–非线性弹簧–阻尼模型的等效跌落数学模型，最后，通过试验和maplesim仿真的方法验证等效跌落数学模型的可行性。

优选地，所述步骤s1)安全跌落高度的跌落测试高度非常小，冲击强度远小于受试商品实物脆值，是非破坏性的，不会破坏受试商品实物。

与现有技术相比，本发明具有以下有益效果：

1、非破坏性测试方法的提出有利于减少包装成本。本发明基于等效跌落理论提出的运输包装件缓冲性能非破坏性测试方法，可以有效地解决测试过程中产品的破坏性问题，从测试源头降低包装成本，提高包装设计效率，将为包装企业带来可观的经济利益。

2、传统试验测试方法与计算机仿真技术的结合具有强强联合效果。本发明综合传统的实验室测试方法与maplesim仿真技术，取长补短，不仅可提高测试效率，还能够有效提高测试精度。

3、研究成果可快速转化为生产力，具有经济效益。本发明提出的maplesim仿真方法操作简单、效率高、生产成本低，易于推广，可在包装生产中被广泛推广应用，从而将本发明快速转化为生产力，具有良好的实用价值。

附图说明

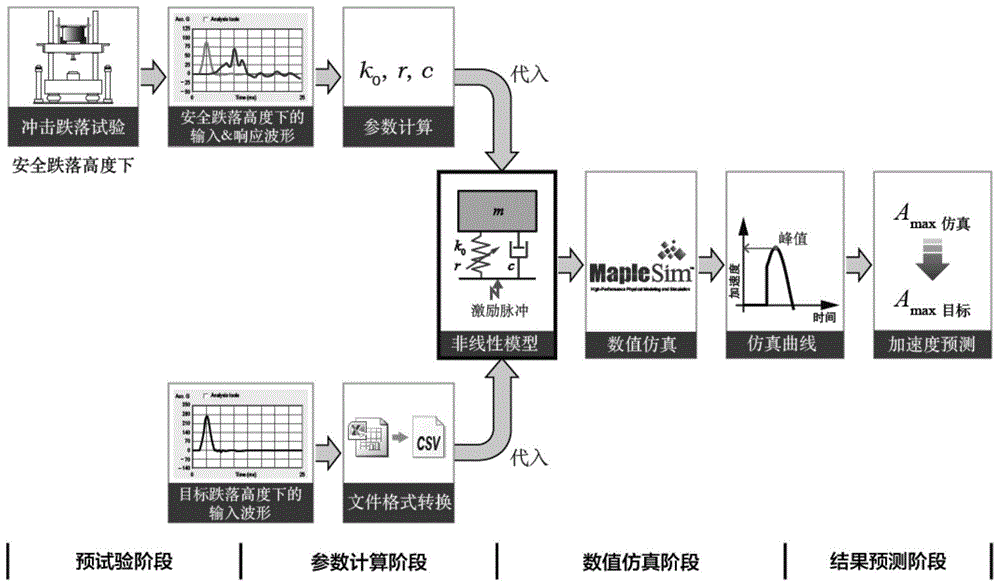
图1本发明的整体流程图；

图2为缓冲包装动力学模型图；

图3为epe材料的力–变形量曲线图；

图4为质量块–非线性弹簧–阻尼模型图；

图5为无阻尼非线性包装系统冲击跌落srs曲线图(包装系统动力学模型、时间–加速度曲线、srs曲线)；

图6质量块–非线性弹簧–阻尼模型图；

图7为有阻尼非线性包装系统冲击跌落srs曲线图(包装系统动力学模型、时间–加速度曲线、srs曲线)；

图8为maplesim仿真模型；

图9为maplesim仿真结果；

图10为目标跌落高度下的响应加速度曲线。

具体实施方式

下面结合附图对本发明做进一步描述：

以下通过具体实施例对本发明作进一步说明，但不用以限制本发明，凡在本发明精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。

实施例

本具体实施方式所述的一种包装件缓冲性能的非破坏性测试方法，其特征在于：包括如下步骤：

s1，首先利用包装件试验样品和冲击跌落试验机进行冲击跌落预试验，进行安全跌落高度的跌落测试记录激励和响应脉冲值，然后进行目标跌落高度的跌落测试并记录激励脉冲；s2，然后根据epe材料的非线性力学模型和等效跌落数学模型模型来进行仿真参数的理论计算和转换；s3，其次从搭建好的maplesim元件库中依次选择所需元件，并对其属性和参数进行设置，依据模型图连接各元件和组件，建立包装件试验样品的仿真模型，进行maplesim仿真，通过安全跌落高度响应加速度值预测目标跌落高度响应加速度值；s4，最后将maplesim仿真值与试验结果值进行比较验证，证明此方法的可行性。具体实施例的整体流程如图1所示。

本实施例中，所述epe材料的非线性力学模型的建立具体步骤如下：

·质量块–非线性弹簧力学模型的建立：

包装件一般由内装物、非线性黏弹性缓冲垫、瓦楞纸箱等外包装组成。为了研究方便一般将其简化为图2所示的缓冲包装动力学模型，其中产品质量为m；缓冲垫弹性系数(a0,b0)；跌落高度为h；位移为y，向下为正方向；为速度；为加速度。缓冲材料以发泡塑料epe为例进行分析，根据不规则型缓冲材料epe的载荷f(y)与变形量y的关系设其动力学方程如式(2.1)所示。

记a＝a0/m，b＝b0/m,(2.2)

则式(2.1)的动力学方程可变形为式(2.3)，

给定初始条件如式(2.4)所示，

取满足初始条件(2.4)的初始试函数可表示为式(2.5)，

y0(t)＝asin(βt)(2.5)

式中，a,β为待定量。

·变分迭代法求解：

现考虑如下式(2.6)所示线性方程，

l[u(x)]+n[u(x)]＝g(x)(2.6)

其中，l为线性算子，n为非线性算子，g为连续函数。

根据变分迭代理论构造如式(2.7)所示的校正泛函。

其中，λ为广义拉式乘子，为限制变分量。

根据上述式(2.6)、(2.7)所述的变分迭代理论对动力学方程式(2.3)构造校正泛函，则校正泛函如式(2.8)所示。

对式(2.8)进行变分，则可得式(2.9)。

同时得到驻值条件(2.10)。

根据式(2.10)解得广义拉氏乘子λ为式(2.11)。

则系统一阶迭代解的位移方程最终表示为式(2.12)和(2.13)的加和。其中，式(2.12)为短解项，式(2.13)为长解项。

令的系数为0，则有式(2.14)成立，此时可消去长解项式(2.13)。

消去长解项后，则系统一阶迭代解的位移方程如式(2.15)所示。

对式(2.15)分别进行一阶和二阶求导，则得到系统一阶迭代解的速度和加速度方程分别如式(2.16)和(2.17)所示。

为求待定参数a、β，对系统一阶迭代解位移方程(即式(2.12)+式(2.13))继续求解，根据长解项系数为0，即式(2.14)，可得β如式(2.18)所示。

联合式(2.16)和式(2.4)中条件，可得在时间t＝0时刻有式(2.19)成立。

联合式(2.14)和式(2.19)，可得式(2.20)。

再将式(2.20)代入式(2.18)中，最终解得β值如式(2.21)。

又已知冲击跌落时间t被定义为式(2.22)，

则当βt＝π/2时，系统的位移和加速度均达到峰值。将t＝π/(2β)代入式(2.16)和(2.17)，

则可得到系统的位移和加速度峰值分别如式(2.23)和(2.24)所示。

·动态压缩试验验证epe材料的非线性动力学模型：

依据gbt8167–87《包装用缓冲材料动态压缩试验方法》，利用缓冲材料试验机(xg–hc，西安广博检测设备有限公司)对试验材料epe进行跌落冲击试验，具体参数设置如下：试验材料为epe，试样尺寸为200mm×200mm，厚度为40mm，重锤质量为10kg，跌落高度为0.8m，并通过传感器记录冲击过程的加速度值和位移值，其代表性数据见表1所示。

表1试验记录加速度值、位移值

将得到的试验数据进行处理，并通过origin进行数据拟合，得到epe的力–变形量曲线如式(2.25)所示，其图形如图3所示。

f(y)＝a0y+b0y³(2.25)

其中拟合参数，a0＝5.62948×10⁴kg/s²，b0＝5.28639×10⁷kg/(m·s)²，则参数a＝5629.48s^-2，b＝5.29×106(m·s)^-2。

试验验证结果分析

根据参数a＝5629.48s^-2，b＝5.29×106(m·s)^-2，得待定参数：振幅a＝0.038m，公式参数β＝105s^-1，再根据已知条件：跌落高度h＝0.8m，重力加速度常数g＝9.8m/s²。将上述条件带入式(2.23)和(2.24)，得位移和加速度峰值分别为：y1max＝0.0395m,g。具体结果见表2所示，可得变分迭代一阶近似解的位移峰值及加速度峰值相对误差分别为2.07％和1.02％。其中，相对误差的计算公式如下：相对误差＝(绝对误差/被测真值)×100％＝(变分迭代结果–试验测量真值/试验测量真值)×100％。

表2试验结果与理论结果比较

研究结果表明：

(1)当跌落高度在0.8m时，非线性动力学方程的位移变分迭代结果与试验实测结果相对误差为2.07％。

(2)当跌落高度为0.8m时，非线性动力学方程的加速度变分迭代结果与试验实测结果相对误差为1.02％。

综上发现，针对新建立的epe非线性力学模型系统的方程解与实际试验结果数值之间相对误差均小于3％，满足要求。说明基于epe缓冲包装系统的质量块–非线性弹簧模型可以用于预测系统跌落冲击位移、加速的峰值等重要参数。

本实施例中，等效跌落数学模型模型的建立具体步骤如下：

·质量块–非线性弹簧模型的等效跌落数学模型

根据缓冲材料性能可将包装系统模型简化为如图4所示的质量块–非线性弹簧模型，其中产品质量为m，缓冲垫的非线性弹簧初始刚度系数为k0，非线性系数为r，跌落高度为h，位移为x，向下为正方向。

①自由跌落试验：

根据能量守恒定律可得内装物在自由跌落状态下，当冲击发生瞬间的势能ep如式(3.8)。

其中，ep是弹簧的弹性势能，xm为弹簧的最大变形量，g为重力加速度常数。

由上式(3.8)可得压缩变形量峰值xm为式(3.9)。

由牛顿第二定律知弹簧在最大变形量时内装物受到的合外力最大。记此弹簧恢复力峰值为fm，则fm可由式(3.10)表示。

由式(3.9)、(3.10)可得，自由跌落的峰值加速度为式(3.11)：

式(3.11)可简记为

afmax＝ωn·v(3.12)

其中，速度v和固有角频率ωn如公式(3.13)所示。

②冲击跌落试验：

在冲击测试中，对系统施加短时的半正弦冲击脉冲，记录系统的srs(shockresponsespectrum，冲击响应谱)曲线，如图5所示。对于srs曲线，当fn·de小于1/2π时，(fn为固有频率，de为有效冲击持续时间)，曲线为过原点的直线。因此，冲击传递率tr可表示为式(3.14)：

其中，acmax为响应加速度峰值，aimax为激励加速度峰值，

对式(3.14)变形可得acmax为响应加速度峰值由式(3.15)表示。

acmax＝2πf0·deaimax＝ω0·deaimax(3.15)

又知非线性系统的初始角频率ω0和速度增量vc分别可由式(3.16)和(3.17)所示，

vc＝deaimax(3.17)

其中，de为有效作用时间，de＝2d/π，d是响应波形的作用时间。

则式(3.15)可表示为式(3.18)。

acmax＝ωn·vc(3.18)

③等效跌落数学模型：

自由跌落测试结果和冲击跌落测试结果在一定条件下是等效的，即当自由跌落速度v等于冲击跌落的速度变化量vc时，自由跌落加速度峰值等于冲击跌落加速度峰值：afmax＝acmaxs，即式(3.12)＝式(3.18)。

·质量块–非线性弹簧–阻尼模型的等效跌落数学模型

将由内装物、缓冲垫、外包装构成的复杂结构的包装件，简化为质量块–非线性弹簧–阻尼包装系统模型，如图6所示。其中产品质量为m，k0为非线性弹簧的初始刚度系数，r为非线性弹簧的非线性系数，阻尼系数为c，跌落高度为h，位移为x，向下为正方向。

①冲击跌落试验：

质量块–非线性弹簧–阻尼模型的动力学方程为式(3.19)：

衰减系数n为式(3.20)，固有角频率ω0为式(3.21)，并引入参数k、ε如式(3.22)，则式(3.19)变形为式(3.23)。

初始条件为式(3.24)

设初始试函数为式(3.25)，其中a为振幅，ω为角频率，ωd为阻尼系统恒定角频率。

x(t)＝ae^ωtsin(ωdt)(3.25)

将上述条件代入式(3.23)，并解该微分方程，可得系统的解如下：

其中，c1，c2，c3，c4，c5，c6，c7为待定系数。

对式(3.26)进行求导得到系统加速度为式(3.27)所示。

其中，阻尼比ξ、阻尼系统角频率ωd、角频率ω、振幅a分别表示为式(3.28)、(3.29)、(3.30)和(3.31)。

w＝-ξω0(3.30)

且当时间t为式(3.32)时，

系统达到加速度峰值为式(3.33)

由牛顿第二定律可知非线性加速度an＝fn/m＝ω0·vn(这里vn为非线性系统速度)，则自由跌落系统的峰值加速度可由公式(3.33)简化为式(3.34)。

afmax＝uf·v·ω0+μf·vn·ω0(3.34)

其中，参数uf和μf均为修正系数，具体定义如下：

另外，非线性加速度an满足式(3.37)，fn为非线性弹簧力；非线性系统速度vn满足式(3.38)。

②冲击跌落试验：

同样，这里包装件被简化为图6所示的非线性弹簧-阻尼缓冲包装动力学模型。对该模型在极短瞬间施加半正弦波脉冲，可得系统的srs曲线如图7c所示。

由图7c可知，当阻尼因素考虑进来后，冲击传递率tr当f0·de很小时不再呈类线性关系，而是如式(3.39)所示。

且为式(3.40)所示。

其中，t0为周期，ω0为固有角频率，a为振幅，参数a＝π/t0，阻尼比ξ满足下式(3.41)，等效角频率ωeq满足下式(3.42)。

对于的求解方法如下：

质量块–非线性弹簧–阻尼模型的动力学方程为式(3.19)，对式(3.19)进行加权平均等效线性化，得到等效后的动力学方程为式(3.43)。

式(3.43)可变形为式(3.44)。

其中，非线性参数ε及阻尼比ξ定义如式(3.45)。

根据式(3.43)和(3.45)，可将动力学方程转化为式(3.46)。

对式(3.46)进行拉普拉斯变换得到式(3.47)。

其中，x(s)、x0(s)为拉普拉斯位移函数，s为复频率。

根据式(3.47)得到位移函数x(s)如下式(3.48)所示。

且当产品的冲击脉冲为正弦波时，其加速度可用式(3.49)表示。

其中，a0为振幅，t0为周期，u(t)为阶跃函数。

对式(3.49)进行拉普拉斯变换得式(3.50)：

其中，a＝π/t0。

根据并结合式(3.50)得式(3.51)，

将式(3.51)代入式(3.48)得式(3.52)。

下面用到了二次跃迁定理和具有高阶极点的拉普拉斯变换，具体如下：

利用第二转换定理中，让则有

在拉普拉斯变换下，式(3.53)变为式(3.54)。

在高阶极点的拉普拉斯变换中，定义：

d(s)＝(s-a1)^k(s-a2)(s-a3)…(s-an)(3.56)

因此，可得式(3.57)

变换得式(3.58)。

因此得式(3.59)。

最终可归纳出式f(t)如式(3.60)所示。

通过第二阶跃定理和高阶极点的拉普拉斯变换，得到位移方程如下式(3.61)所示。

x(t)＝a0a[g(t)·u(t)+g(t-t0)·u(t-t0)](3.61)

又因为u(t)为阶跃函数，定义为

故有

将式(3.62)和(3.63)带入(3.61)得式(3.64)：

对式(3.64)进行二次求导得到加速度如式(3.65)所示：

令α和β关系如式(3.66)所示，

并将(3.66)带入(3.52)得到x(s)如式(3.67)所示：

其中，

将式(3.68)中的6个条件带入(3.60)中，则g(t)可表示为式(3.69)。

对式(3.69)进行二次求导，可得如式(3.70)所示。

令其中parti为式(3.71)，

根据下式

联合式(3.71)和(3.72)，可得parti

又有

e^ix＝cosx+isinx(3.75)

联合式(3.73)、(3.74)和(3.75)，parti变形为式(3.76)。

另一方面，partп为下式(3.77)

令

将(3.78)带入(3.77)得到partп为式(3.79)

综上所述得到的实部为式(3.80)所示。

由线性等效跌落数学模型可知，当一个弹簧刚度为k0+衰减系数为c+质量为m的线性系统受到一激励加速度aimax的半正弦脉冲冲击时，其srs曲线如图5c所示。由图5c可知，当fn·de小于1/2π时，srs是过原点的直线。因此其冲击传递率tr可被定义为式(3.81)。

其中，ω0＝2πf0，de为有效作用时间，de＝2d/π，d是响应波形的持续时间。

记当一个非线性弹簧(弹簧刚度为k0，非线性系数为r)+衰减系数为c+质量为m的非线性系统受到同一激励加速度aimax的半正弦脉冲冲击时，其响应加速度为acmax。

这里引入修正系数nc，使得

acmax＝nc·acmax0(3.82)

将式(3.82)代入式(3.81)，变形可得式(3.83)。

acmax＝nc·ω0·vc(3.83)

这里，ω0为系统初始角频率，vc为速度增量。

③等效跌落数学模型：

综上可知，自由跌落加速度峰值afmax可由式(3.34)表示，冲击跌落加速度峰值acmax可由式(3.83)表示。故，对于非线性弹簧-阻尼模型而言，自由跌落和冲击跌落的等效条件为

其中，nc为冲击跌落系数，uf、μf分别为自由跌落的线性和非线性系数，v和vn分别为冲击跌落线性速度峰值和非线性速度峰值。

·等效跌落数学模型的验证：

通过实验验证和maplesim仿真验证的方法，证明等效跌落数学模型的可靠性，具体步骤如下：

1)实验室试验：

(1)进行冲击跌落试验并通过数据采集设备记录冲击激励和响应数据；

(2)进行动态压缩试验并通过数据采集设备记录动态压缩的激励和响应数据；

(3)通过校正公式(4.1)将动态压缩速度v校正为新速度vnew；

(4)重复速度为vnew的动态压缩试验，并测量加速度值。

(5)处理和分析试验数据。

2)maplesim仿真试验：

(1)分别进行冲击跌落试验和动态压缩试验的模型仿真，得到仿真结果，进行数据处理和分析。结果对比分析：

(2)比较试验和仿真结果并评估等效跌落数学模型。

本实施例中，所述步骤s21，根据实验数据计算模型参数：非线性弹簧刚度系数k0、非线性系数r、阻尼系数c，其具体方法如下：

①k0、r的计算需用到仿真软件maplesim，即对maplesim中自定义的非线性弹簧–阻尼器元件中的非线性弹簧初始刚度系数k0、非线性系数r、阻尼系数c进行处理分析：首先，通过阻尼比ξ计算固定阻尼系数c的值；然后改变非线性参数k0、r的值，进而得到不同的仿真结果，进行多次仿真直到仿真结果与实际冲击跌落试验测试中的试验结果一致，从而确定参数k0、r的最终值。

②阻尼系数c：表3展示了冲击跌落试验的速度v(满足)和等效跌落理论中的校正速度vnew(满足公式4.1)的数值比较，可得基于等效跌落数学模型修正前后速度间的误差为±0.5m/s，vnew近似等于v。因此，可以通过vnew＝v和公式(4.1)结合得到阻尼系数c的值。

表3基于等效跌落数学模型修正前后速度v的对比

具体方法如下：

跌落高度在0.2m时，vnew＝v＝1.98m/s，且速度vnew满足公式(4.1)。

其中，nc为冲击跌落系数、uf、μf为自由跌落的线性和非线性系数，vc为冲击跌落速度变化量，vn为非线性速度峰值。

(1)计算nc。

根据前述内容知nc满足式(4.2)。

冲击传递率tr为式(4.3)。

其中，ac为响应加速度，ai为激励加速度。根据冲击跌落试验数据得知ai＝59.25g，ac＝29.22g。因此，tr＝0.49。

根据冲击跌落试验的激励–时间曲线可得到有效持续时间de为式(4.4)：

其中，激励时间d＝7.12ms，所以得到有效持续时间de＝4.54ms。

根据冲击跌落试验的响应–时间曲线可得到固有频率fn为式(4.5)：

其中，响应时间t＝16.28ms，所以得到固有频率fn＝0.03ms。

因此，将各个参数带入到公式(4.2)可得到参数nc＝0.56。

(2)计算非线性速度vn，满足式(4.6)

经前述k0和r的仿真方法，确定k0＝3×10⁵n/m；r＝1.05×10⁷n/m³。另外，最大变形量x为28.9mm，产品质量m为7.6kg，固有频率fn为0.03ms，从而可得非线性速度vn＝7.64m/s。

(3)冲击跌落试验时的速度变化量vc为1.98m/s。

(4)参数uf和μf满足前述内容中的式(3.35)和式(3.36)。

将(1)、(2)、(3)、(4)得到的各参数带入式(4.1)，可得阻尼比ξ＝0.45。

因此，根据公式(4.7)得阻尼系数c＝1359。

本实施例中，进行maplesim数值仿真，主要通过以下三步：

(1)建立质量块–非线性弹簧–阻尼器模型；

(2)输入参数；

(3)进行仿真。

仿真模型如图8所示，其中①probe为探针，用来记录仿真结果；②m为产品质量，输入值为7.6kg；③自定义元件为非线性弹簧和阻尼器的组合元件，仿真参数k即上述非线性弹簧初始刚度系数k0，为3×10⁵n/m，仿真参数r即上述非线性系数r，为1.05×10⁷n/m³，仿真参数d即上述阻尼系数c，为1359；④为加速度组件；⑤时间序列查询表组件用于添加目标跌落高度下的输入脉冲数据。

仿真结果如图9所示。由仿真数据可知，仿真结果的响应峰值加速度为57.26g。

·预测和验证

由仿真数据可知，仿真结果的响应峰值加速度为57.26g，即预测目标跌落高度的峰值加速度amax仿真＝57.26g。

作为验证试验的第二次冲击跌落试验，其目标跌落高度下的响应加速度曲线如图10所示，可知实验峰值加速度值amax目标＝57.89g。将仿真预测值和验证试验值进行对比，可知预测误差为1.09％，因此可以证明混合跌落测试方法可行。

市场前景及产业化后经济、社会效益预期

(1)市场前景

近年伴随着我国电商经济和物流业的飞速发展，物流包装作为保护商品的主要技术手段越发显得重要，但这一发展进程中并非全是喜讯。其中，国内尚不完善的物流环境大大增加了产品破损的可能性，每年因物流包装不当造成的经济损失是非常惨痛的。据统计，仅近5年因包装在物流过程中的破损，给我国造成的直接经济损失高达100亿元/年以上。与此同时，日益扩大的需求所造成的包装垃圾随着国内境的恶化而日益受到人们的关注，由此绿色物流包装越来越受到青睐。而另一方面，国内人口红利的优势不再，市场竞争要求物流包装尽可能地降低成本。上述社会需求对物流包装提出了“质优”(足够的保护性能)、“绿色”(环保无公害)和“价廉”(降低设计与生产成本)的要求，如何设计满足上述需求的物流包装已成为物流与包装两大领域的研究课题，而新型物流包装的产生离不开包装性能测试技术的发展。可见，本项目具有广阔的市场前景。

(2)产业化后的经济效益

对于普通商品如洗发水而言，传统的包装件缓冲性能测试试验成本一般在千元水平：但对于价格昂贵产品来说，基于目前试验方法的测试成本非常高。例如，—台具有打印、复印、扫描及传真功能的彩色多功能数码复合机，其市价约在35万元/台左右。若按传统测试方法，一般至少需进行3次测试试验才能最终满足设计要求，其测试试验成本高达35×3＝105万元。对于更贵重产品而言，测试成本将会更高。基于本发明成果，该多功能数码复合机的测试只需一台多功能数码复合机实物和少量缓冲材料进行预试验，然后进行数据转换，最后进行仿真计算出最终试验结果。整个测试过程只在预试验阶段用到商品实物，而该阶段不存在破坏性，故其成本组成仅包含一台多功能数码复合机(约35万元)+缓冲材料和试验设备使用成本(约为0.1万元)，预计可使测试成本降低60％左右，从而降低可观的企业生产成本。

(3)产业化后的社会效益

本发明的主要内容之一是研究绿色物流包装材料的非线性缓冲特性，项目成果可促进绿色包装材料的防护精度，可有效扩大其市场占有率，这无疑可以在很人程度上缓解国内环境污染的压力，进而收到良好的社会效益。

以上显示和描述了本发明的基本原理、主要特征以及本发明的优点。本行业的技术人员应该了解，本发明不受上述实施例的限制，上述实施例和说明书中描述的只是说明本发明的原理，在不脱离本发明精神和范围的前提下，本发明还会有各种变化和改进，这些变化和改进都落入要求保护的本发明范围内。本发明要求保护范围由所附的权利要求书及其等效物界定。