一种利用底视差分干涉测量二维地形坡度的方法与流程

本发明涉及天基雷达技术领域，具体涉及一种星载微波雷达的高精度小地形坡度测量(测量精度优于0.0001°)，比如南北极冰架地形坡度(<3°)和海洋地形坡度(<0.1°)测量的方法，特别涉及一种利用底视差分干涉测量二维地形坡度的方法。

背景技术：

自2004年以来，科学界正在朝绘制高分辨率高精度(1mgal)全球重力场努力；同时南北极冰面高测量精度也需要进一步提高。这两者都需要高精度的地形坡度信息。

目前可以用于海洋坡度测绘的雷达主要是星载微波高度计，比如国际国内现有的实孔径雷达高度计和近年来发展的3种新型雷达高度计——底视合成孔径雷达高度计，底视干涉合成孔径雷达高度计和宽刈幅小入射角干涉成像雷达高度计。

(1)星载底视合成孔径雷达高度计。在传统实孔径雷达高度计的基础上，国外提出并研制了底视合成孔径高度计，比如欧空局在轨雷达高度计sentinel-3(国内译称哨兵3号)。用于观测卫星正下方海面的平均高度，有效波高和后向散射系数，进而生成全球海面高程，海面波高，海面风速，海面坡度和海洋重力场产品。

星载底视合成孔径雷达高度计可以测量沿轨方向的海洋坡度，但不能同时测量沿轨方向和交轨方向二维海面地形坡度。

(2)星载底视合成孔径干涉雷达高度计，比如欧空局的在轨雷达高度计cryosat-2。其工作模式分为底视实孔径模式，底视合成孔径模式和底视干涉合成孔径模式。其中底视干涉合成孔径模式主要用于南北极冰架地形坡度测量。

理论上讲，该仪器可以实现对二维地形坡度测绘。但是由于地形坡度和基线横滚角耦合在一起共同影响干涉相位，因此它只能依赖于星上星敏感器，和对星敏感器的定标，而定标后的星敏感器精度只有100urad量级(1s平均)。因此，该仪器只能满足测冰架坡度的需求，但无法实现高精度(1urad)二维海洋地形坡度测量。

(3)天基(星载)干涉成像雷达高度计。小入射角干涉成像高度计(比如国内天宫-2号的三维成像高度计，国外的swot高度计)的主要优势在于，由于采用了小入射角观测方式，相比前述底视雷达高度计，在同样的轨道高度上，其观测刈幅可以提高8倍左右，从而实现二维海面高成像，对于海洋动力学具有重要意义。代价是，测高精度比底视雷达高度计(比如传统实孔径雷达高度计，底视合成孔径高度计)有所下降。

由于海洋地形坡度非常小，而成像高度计测高精度随着远离天底点而变差，所以不能实现高精度(urad量级)二维海面地形坡度测量。

技术实现要素：

本发明的目的在于克服现有雷达高度计技术无法实现高精度二维地形坡度测绘的问题，尤其是海洋坡度测绘；提出了一种利用底视差分干涉测量二维地形坡度的方法。

为实现上述目的，本发明的实施例1提出了一种利用底视差分干涉测量二维地形坡度的方法，所述方法包括：

对星载雷达的左边天线al、中间天线ao和右边天线ar接收的回波进行方位向-距离向压缩处理，得到三个天线压缩处理后的脉冲回波；

对压缩处理后的脉冲回波进行干涉处理，得到两个干涉回波；

对两个干涉回波分别进行方位向-距离向二维平滑；

从平滑后的干涉回波中提取alar干涉相位；

基于多个alar干涉相位，利用最小二乘算法估计出横轨方向坡度角；

利用回波输出的地形跟踪高程和对应的地面网格单元距离之比，计算地面网格单元上的顺轨方向坡度角。

作为上述方法的一种改进，所述对压缩处理后的脉冲回波进行干涉处理，得到两个干涉回波；具体包括：

其中，为天线ao接收的第i个回波脉冲的第j个距离门的回波；为天线al接收的第i个回波脉冲的第j个距离门的回波；为ar天线接收的第i个回波脉冲的第j个距离门的回波；为天线ao和天线al之间第i个干涉回波脉冲的第j个距离门的干涉回波，为天线ao和天线ar之间第i个干涉回波脉冲的第j个距离门的干涉回波。

作为上述方法的一种改进，所述从平滑后的干涉回波中提取alar干涉相位；具体包括：

从干涉回波中提取的干涉相位为：

从干涉回波中提取的干涉相位为：

其中，()为取相位函数；n1，n2分别表示参与求和平均的方位向脉冲数目和参与平均的距离门数目；mij为第i个回波脉冲的第j个距离门，跟踪门标号为j0；

alar干涉相位为：

其中，k为电磁波波数，b为基线长度，即左边天线al相位中心和右边天线ar相位中心的距离。

作为上述方法的一种改进，所述基于多个alar干涉相位，利用最小二乘算法估计出横轨方向坡度角；具体包括：

alar干涉相位与横轨方向坡度角β的关系为：

其中，d，e，f为雷达系统及平台参数，σh为地表均方根高度；

利用多个干涉相位和最小二乘法，估计出横轨方向坡度角β。

本发明的实施例2提出了一种利用底视差分干涉测量二维地形坡度的方法，所述方法包括：

对星载雷达的左边天线al、中间天线ao、右边雷达天线ar、后向天线aa和前向天线af接收的回波进行方位向-距离向压缩处理，得到五个天线压缩处理后的脉冲回波；

对压缩处理后的脉冲回波进行干涉处理，得到四个干涉回波；

对四个干涉回波分别进行方位向-距离向二维平滑；

从平滑后的干涉回波中提取alar干涉相位以及aaaf干涉相位；

基于多个alar干涉相位，利用最小二乘算法估计出横轨方向坡度角；

基于多个aaaf干涉相位，利用最小二乘算法估计出顺轨方向坡度角。

作为上述方法的一种改进，所述对压缩处理后的脉冲回波进行干涉处理，得到四个干涉回波；具体包括：

其中，为ao天线接收的第i个回波脉冲的第j个距离门的回波；为al天线接收的第i个回波脉冲的第j个距离门的回波；为ar天线接收的第i个回波脉冲的第j个距离门的回波；为aa天线接收的第i个回波脉冲的第j个距离门的回波；为af天线接收的第i个回波脉冲的第j个距离门的回波；为ao天线和al天线之间第i个干涉回波脉冲的第j个距离门的回波；为ao天线和ar天线之间的第i个干涉回波脉冲的第j个距离门的回波；为ao天线和aa天线之间的第i个干涉回波脉冲的第j个距离门的回波；为ao天线和af天线之间的第i个干涉回波脉冲的第j个距离门的回波。

作为上述方法的一种改进，其特征在于，所述从平滑后的干涉回波中提取alar干涉相位以及aaaf干涉相位；具体包括：

从干涉回波中提取的干涉相位为：

从干涉回波中提取的干涉相位为：

从干涉回波中提取的干涉相位ψoa(mij0)为：

从干涉回波中提取的干涉相位ψof(mij0)为：

其中，()为取相位函数；n1，n2分别表示参与求和平均的方位向脉冲数目和参与平均的距离门数目；mij为第i个回波脉冲的第j个距离门，跟踪门标号为j0；

alar干涉相位为：

aaaf干涉相位为：

其中，k为电磁波波数，b为基线长度，即左边天线al相位中心和右边天线ar相位中心的距离。

作为上述方法的一种改进，所述基于多个alar干涉相位，利用最小二乘算法估计出横轨方向坡度角；基于多个aaaf干涉相位，利用最小二乘算法估计出顺轨方向坡度角；具体包括：

alar干涉相位与横轨方向坡度角β的关系为：

其中，d，e，f为雷达系统及平台参数，σh为地表均方根高度；

利用多个alar干涉相位和最小二乘法，估计出横轨方向坡度角β；

aaaf干涉相位与顺轨方向地形坡度角的关系为：

其中，r,s,t为雷达系统及平台参数，σh为地表均方根高度；

利用多个aaaf干涉相位以及最小二乘法，估计出顺轨方向地形坡度角

本发明的实施例3提出了一种利用底视差分干涉测量二维地形坡度的方法，所述方法包括：

对星载雷达的左边天线al、中间天线ao、右边天线ar、后向天线aa和前向天线af接收的回波进行方位向-距离向压缩处理，得到五个天线压缩处理后的脉冲回波；

对压缩处理后的脉冲回波进行干涉处理，得到四个干涉回波；

对四个干涉回波分别进行方位向-距离向二维平滑；

从平滑后的干涉回波中提取alar干涉相位以及aaaf干涉相位；

基于多个alar干涉相位，利用最小二乘算法估计出横轨方向坡度角；

基于多个aaaf干涉相位，利用最小二乘算法估计出第一顺轨方向坡度角。

利用回波输出的地形跟踪高程和对应的地面网格单元距离之比，计算地面网格单元上的第二顺轨方向坡度角；

将第一顺轨方向坡度角和第二顺轨方向坡度角进行加权平均，得到最终的顺轨方向坡度角。

作为上述方法的一种改进，所述将第一顺轨方向坡度角和第二顺轨方向坡度角进行加权平均，得到最终的顺轨方向坡度角，具体包括：

将第一顺轨方向坡度角和第二顺轨方向坡度角进行加权平均：

其中，为最终的顺轨方向坡度角；

其中，和分别是第一顺轨方向坡度角的测量方法对应的标准差和方差；和是第二顺轨方向坡度角的测量方法对应的标准差和方差。

本发明的优势在于：

1、本发明的方法建立了更接近测量几何关系和物理测量过程的严谨数学模型，并基于模型的数学特征完成系统设计，实现误差对消；

2、本发明的方法可在<5公里的空间尺度上以urad量级的地形坡度测量精度，实现二维海面(/冰架)地形坡度测量，这是目前其它测量手段无法实现的；

3、在测量海洋地形坡度和南北极冰架地形坡度时，在相对宽松的工程实现条件下，本发明的方法可以通过误差对消剔除基线机械形变，横滚角和俯仰角对地形坡度测量的影响，比现有其它方法显著提高地形坡度测量精度；

4、和基于测高实现海洋地形坡度绘制的雷达高度计设备不同，本发明的方法在星载实现过程中，直接测量二维海面坡度，因此不需要为了实现高精度测距而必需的激光反射阵列、doris系统和校正辐射计系统等；也不需要宽刈幅小入射角干涉高度计等对基线的苛刻要求和专用定标场；工程实现成本比利用高度计通过高程测量反演地形坡度的方法成本显著下降。

附图说明

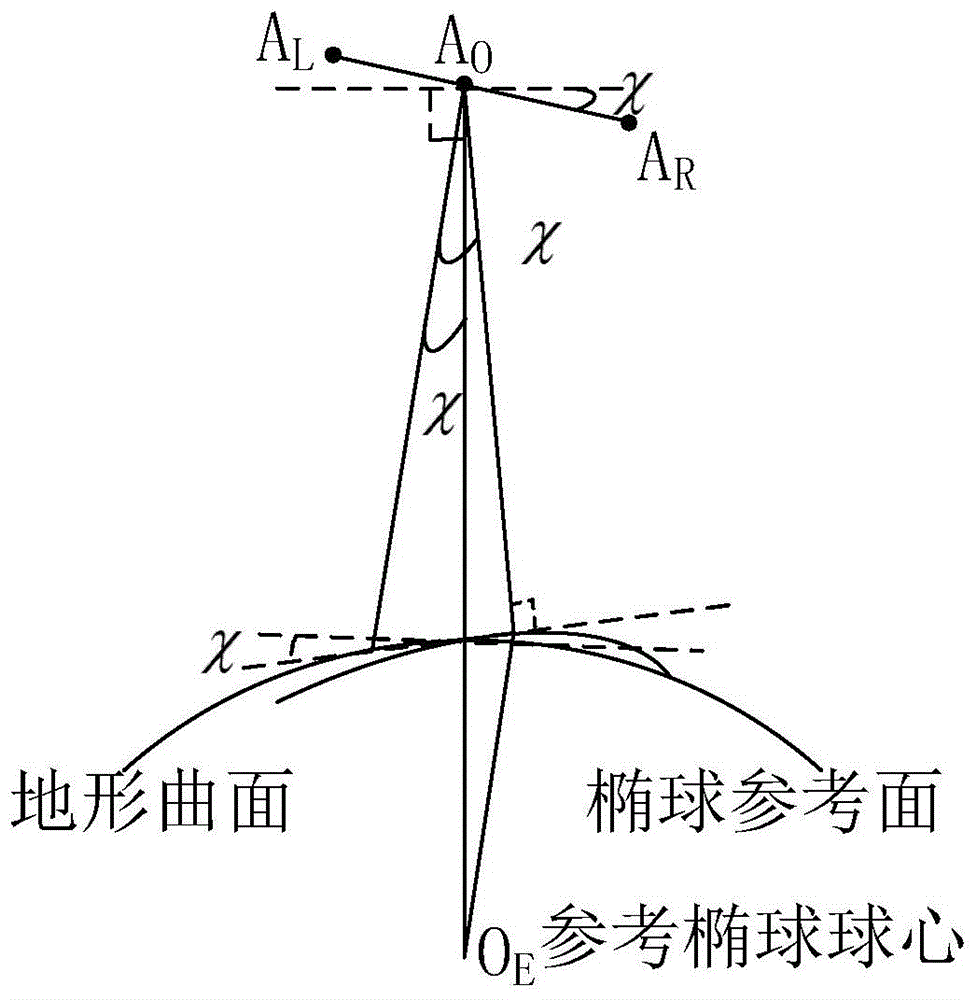
图1为二维海面地形坡度测量示意图；

图2为几何观测模型示意图；

图3为ao天线接收的回波及其跟踪点示意图；

图4为横滚角对应的相位示意图；

图5为地形坡度对应的相位示意图；

图6为仿真的横轨向地形坡度估计结果示意图；

图7为在顺轨和横轨方向上都采用差分干涉技术的方案示意图。

具体实施方式

下面结合附图和具体实施例对本发明的技术方案进行详细说明。

实施例1

被观测地形坡度和基线矢量的几何关系如图1所描述(为了显示清楚，图中角度和高度的比例关系失真，但是不影响问题本质和问题描述)。雷达垂直纸面向里飞行，天线al,ao,ar接收地面反射的电磁波。根据干涉测量理论，可以知道天线alar干涉回波相位ψ对应的干涉角φ(χ,β,σh)(φ＝ψ/(k·b)，其中k为电磁波圆波数，b为基线长度)是天线基线横滚角χ，地形坡度角β(各参数定义在后文中描述)和本地均方根高度σh的函数。因此，只要建立回波相位和天线横滚角，地形坡度之间的数学关系，就可以从中求解出天线横滚角和横轨方向的坡度角。

本发明的理论基础是建立的回波模型和回波相位模型。基于图1所示的底视干涉雷达高度计系统可以实现横轨方向上urad量级的地形坡度测量精度(后文给出证明)。因此，基于图1所示的底视干涉雷达系统可以实现高精度二维海面(/冰面)坡度测量。

下面描述本发明的理论基础。基于图2所示的几何观测模型和图1描述的几何关系，可以建立所需数学模型。

在图2中，天线基线长度b。雷达天线ao位于基线中心，其天底点为n，雷达天线ao相对于天底点n的高度为h，天底点n的本地地球半径为re。基线方向自雷达天线al指向雷达天线ar，和x轴方向相同。雷达沿y轴方向飞行，横滚角χ，逆着飞行方向看，逆时针为正(即当χ>0时，逆飞行方向看，左侧天线al高于右侧天线ar)。天线俯仰角μ，逆着x轴看，逆时针为正(即当μ>0时，雷达视轴为前视)。基线偏航角为ζ，当逆着z轴看时(即下视方向上)，逆时针为正(即当ζ>0时，左侧天线al在后，右侧天线ar在前)。点目标t的球坐标为其中表示点目标t高出参考球面的高度。点目标所在平面即过点的切平面，与过点的切平面在横轨方向上(x轴方向上)的夹角，被定义为横轨方向的坡度角β，β的方向定义和横滚角χ相同；其在沿轨(顺轨)方向上的坡度角为的方向定义和俯仰角μ相同。

基线与卫星到天底点连线和飞行速度构成的平面垂直。3个天线相位中心分别位于图1中ao,al,ar所在位置，且aoal子基线和aoar子基线对称(这里的对称是指几何对称，同时机械和热形变参数相同。虽然两个子基线长度不等也可以通过计算修正。但是两子基线长度相等便于计算，因此这里假设两子基线长度相等)。3个天线视轴在同一平面内，且互相平行。中间天线ao视轴在卫星到天底点连线和飞行速度构成的平面内且平行于卫星到天底点连线。天线ao发射电磁脉冲，ao,al,ar3个天线同时接收地面反射的雷达回波。其中，天线馈源应该和基线分离，以最小化基线变形对基线长度的影响。

针对上述几何观测模型和物理模型，可以得到干涉回波相位：

其中，表示雷达天线ao和雷达天线al之间的干涉回波相位；表示雷达天线ao和雷达天线ar之间的干涉回波相位。η＝1+h/re为本地地球曲率，σh为本地均方根高度。τ是雷达回波检测距离门对应的回波延迟。在回波延迟τ＝0处，根据(1)式，可以得到差分干涉：

和

可以进一步把(2-1)式和(3-1)式写为

其中，a、b、c是雷达系统相关的参数；d、e、f是雷达系统和平台参数。

利用(2-2)式，可以得到横滚角χ，然后利用(3-2)式可以计算横轨方向的坡度角β。在大样本条件下，上述系统的横轨方向坡度角β的测量精度为，

其中ηc为干涉回波的相干系数，对于海洋，一般超过0.95。n则为独立观测脉冲数，对于采用底视合成孔径处理的雷达系统，在2km尺度上可以获得9000个左右独立样本数目。因此，二维地形坡度角的测量精度可以达到urad量级。

在顺轨方向上，根据雷达高度计测量的各个星下点高程h(x)以及各个星下测量点之间的距离δx，计算出顺轨地形坡度采用底视合成孔径雷达高度计技术，在公里量级的空间尺度上，可以实现厘米量级的地面高程测量，因此可以实现顺轨方向上urad量级的地形坡度测量精度。

针对前文所述测量方案，以系统参数800km轨道高度，ka波段，基线长度2m(基线长度被定义为al,ar两个天线相位中心之间的距离)，脉冲重复频率9khz，信号带宽320mhz为例，介绍具体的技术实施方式。

按照如下方式实施底视差分干涉测量即可实现二维海面(冰面)的高精度地形坡度测量。在以ao为发射天线，并以设计脉冲重复频率prf朝地面发射电磁脉冲。3个天线同时接收地面反射回波，记为ψ0,ψl,ψr；对ψ0(也可以为ψl或ψr)回波进行方位向-距离向压缩处理(或者只进行距离向压缩处理)，并对处理后回波进行在轨跟踪，保持锁定目标回波信号。处理过程如下：

1、对接收的回波ψ0,ψl,ψr均进行方位向-距离向压缩处理，并对ao(也可以为其它两个天线中的任一个)接收回波进行高精度重跟踪处理。记第i个回波脉冲的第j个距离门为mij，跟踪门标号为j0。同时输出对应的地表均方根高度σh。参见附图3所示跟踪距离门。

2、对压缩处理后的脉冲回波进行干涉处理，得到：

其中，为ao天线接收的第i个回波脉冲的第j个距离门的回波；为al天线接收的第i个回波脉冲的第j个距离门的回波；为ar天线接收的第i个回波脉冲的第j个距离门的回波；为ao天线和al天线之间第i个干涉回波脉冲的第j个距离门的回波，为ao天线和ar天线之间的第i个干涉回波脉冲的第j个距离门的回波。

3、对和进行方位向-距离向二维平滑。

4、提取干涉相位：

其中，()为取相位函数；n1，n2分别表示参与求和平均的方位向脉冲数目和距离门数目。

5、按照(2)式，对于第i组回波(ao,al,ar3个天线接收到的第i个回波为一组)可以得到差分干涉相位

参见附例图4给出的相位。

6、对多个差分干涉相位利用最小二乘算法估计出横滚角χ和系统参数a,b,c。

7、对每组回波计算alar干涉相位

参见附图5给出的相位。

8、对多个利用最小二乘估计出横轨方向地形坡度角β和雷达系统及平台参数d,e,f。参见附图6给出的地形坡度角估计。

9、在顺轨方向上，利用测量回波输出的地形跟踪高程，和对应的地面网格单元距离之比，给定地面网格单元上的顺轨方向坡度

其中，h(x1)是顺轨方向坐标x1处的地表高程，h(x2)是顺轨方向坐标x2处的地表高程。利用雷达高度计测量地表高程h(x1)，h(x2)是一个成熟的技术。

鉴于目前尚没有这样一个星载底视差分干涉观测雷达系统，可以设计仿真实验来验证。在仿真中，横轨向设置了7个地形坡度。仿真参数如下表1所示。

表1仿真参数

根据上述参数进行仿真，仿真结果如图3-图6所示。图3是ao天线接收到的回波及其跟踪点。图4是横滚角对应的差分干涉相位。图5是地形坡度角对应的干涉相位。图6是对仿真的横轨向地形坡度角估计的估计。

实施例2

在顺轨方向上也采用如上所述差分干涉技术，从而整体方案如图7所示，基线afaa和前述基线alar在同一平面内，且相互垂直；afaa基线长度与alar基线长度相同。顺轨方向的差分干涉技术实施方式和第一种方案中的横轨方向的差分干涉技术实施方式相同。

针对上述几何观测模型和物理模型，可以得到干涉回波相位：

其中，表示雷达天线ao和雷达天线aa之间的干涉回波相位；表示雷达天线ao和雷达天线af之间的干涉回波相位。η＝1+h/re为本地地球曲率，σh为本地均方根高度。τ是雷达回波检测距离门对应的回波延迟。在回波延迟τ＝0处，根据(4)式，可以得到差分干涉：

和

可以进一步把(5-1)式和(6-1)式写为

其中，l，m,n是雷达系统相关的参数；r，s,t是雷达系统及平台相关的参数。

针对前文所述测量方案，以系统参数800km轨道高度，ka波段，基线长度2m(基线长度被定义为al,ar两个天线相位中心之间的距离)，脉冲重复频率9khz，信号带宽320mhz为例，介绍具体的技术实施方式。

按照如下方式实施底视差分干涉测量即可实现二维海面(冰面)的高精度地形坡度测量。在以ao为发射天线，并以设计脉冲重复频率prf朝地面发射电磁脉冲。5个天线同时接收地面反射回波，记为ψo，ψl，ψr，ψa，ψf；对ψo(也可以为ψl，ψr，ψa，ψf中任意一个)回波进行方位向-距离向压缩处理(或者只进行距离向压缩处理)，并对处理后回波进行在轨跟踪，保持锁定目标回波信号。然后进行如下处理过程：

1、对ψo，ψl，ψr，ψa,ψf回波进行方位向-距离向压缩处理，并对ao天线(其它四个天线中的任意一个)接收回波进行高精度重跟踪处理。记第i个回波脉冲的第j个距离门为mij，跟踪门标号为j0。同时输出对应的地表均方根高度σh。参见附图4所示跟踪距离门。

2、对压缩处理后的脉冲回波进行干涉处理，得到：

其中，为ao天线接收的第i个回波脉冲的第j个距离门的回波；为al天线接收的第i个回波脉冲的第j个距离门的回波；为ar天线接收的第i个回波脉冲的第j个距离门的回波；为aa天线接收的第i个回波脉冲的第j个距离门的回波；为af天线接收的第i个回波脉冲的第j个距离门的回波；为ao天线和al天线之间第i个干涉回波脉冲的第j个距离门的回波；为ao天线和ar天线之间的第i个干涉回波脉冲的第j个距离门的回波；为ao天线和aa天线之间的第i个干涉回波脉冲的第j个距离门的回波。为ao天线和af天线之间的第i个干涉回波脉冲的第j个距离门的回波。

3、对和进行方位向-距离向二维平滑。

4、提取干涉相位：

其中，()为取相位函数；n1，n2分别表示参与求和平均的方位向脉冲数目和距离门数目。

5、按照(2)式，对于第i组回波(ao,al,ar,af,aa5个天线接收到的第i个回波为一组)计算得到alar干涉相位和aaaf干涉相位

6、对多个利用最小二乘估计出横轨方向地形坡度角β和系统参数d，e，f。

7、对多个利用最小二乘估计出顺轨方向地形坡度角和系统参数r，s，t。

实施例3

在顺轨方向上采用如上所述差分干涉技术，同时进行天底点高程测量。从而整体方案如图7所示，基线afaa和前述基线alar在同一平面内，且相互垂直。这样做的优点是，可以使得顺轨方向地形坡度精度进一步提高。原因有两点：一是相位信息和高程信息相互独立；二是可以避免由于第一种方案在顺轨方向上测量高程时没有考虑目标海面坡度带来的高程误差而导致的坡度误差。根据现有海面高观测资料，绝大部分海域海面坡度导致的高程测量误差只有mm量级，但是在某些海域，这一误差可以达到cm量级，从而使得坡度误差超过1urad。这种方案的代价是系统复杂度和经济成本更高。

按照如下方式实施底视差分干涉测量即可实现二维海面(冰面)的高精度地形坡度测量。在以ao为发射天线，并以设计脉冲重复频率prf朝地面发射电磁脉冲。5个天线同时接收地面反射回波，记为ψo，ψl，ψr，ψa，ψf；对ψo(也可以为ψl，ψr，ψa，ψf中任意一个)进行方位向-距离向压缩处理(或者只进行距离向压缩处理)，并对处理后回波进行在轨跟踪，保持锁定目标回波信号。然后进行如下处理过程：

1、对ψo，ψl，ψr，ψa，ψf回波进行方位向-距离向压缩处理，并对ao天线(或对其它四个天线的任意一个)接收回波进行高精度重跟踪处理。记第i个回波脉冲的第j个距离门为mij，跟踪门标号为j0。同时输出对应的地表均方根高度σh。

2、对压缩处理后的脉冲回波进行干涉处理，得到：

其中，为ao天线接收的第i个回波脉冲的第j个距离门的回波；为al天线接收的第i个回波脉冲的第j个距离门的回波；为ar天线接收的第i个回波脉冲的第j个距离门的回波；为aa天线接收的第i个回波脉冲的第j个距离门的回波；为af天线接收的第i个回波脉冲的第j个距离门的回波；为ao天线和al天线之间第i个干涉回波脉冲的第j个距离门的回波；为ao天线和ar天线之间的第i个干涉回波脉冲的第j个距离门的回波；为ao天线和aa天线之间的第i个干涉回波脉冲的第j个距离门的回波。为ao天线和af天线之间的第i个干涉回波脉冲的第j个距离门的回波。

3、对和进行方位向-距离向二维平滑。

4、提取干涉相位：

其中，()为取相位函数；n1，n2分别表示参与求和平均的方位向脉冲数目和距离门数目。

5、按照(2)式，对于第i组回波(ao,al,ar,af,aa5个天线接收到的第i个回波为1组)计算得到alar干涉相位和aaaf干涉相位

6、对多个利用最小二乘估计出横轨方向坡度角β和系统参数d，e，f。

7、多个利用最小二乘估计出第一顺轨方向坡度角和系统参数r，s，t。

8、利用测量回波输出的地形跟踪高程，和对应的地面网格单元距离之比，给定地面网格单元上的第二顺轨方向坡度角

9、将第一顺轨方向坡度角和第二顺轨方向坡度角进行加权平均：

其中和分别是两种测量方法对应的标准差和方差。

本发明的创新点在于：

1、对参加底视差分干涉处理的雷达天线接收到的回波，在同一参考系下对各天线回波进行建模，从而得到底视干涉雷达回波模型，和底视差分干涉相位模型。这既是本发明的创新点，也是本发明的理论基础。

2、根据底视干涉相位的对称性，通过采用对称双基线构建差分干涉方程组，将目标地形坡度和横滚角从干涉相位中分离(/解耦)出来，是本发明的理论创新和技术创新。

3、在横轨和顺轨方向上利用底视对称基线3接收通道(如图7所示)测量二维地形坡度是本发明的技术创新。利用对称基线的优点是可以在观测地形坡度时实现基线形变误差对消和卫星平台横滚角对消以及卫星平台俯仰角对消，减少测量误差。

4、通过底视差分干涉回波反演高精度地形坡度的处理步骤(流程)，是本发明的第4个创新点。

最后所应说明的是，以上实施例仅用以说明本发明的技术方案而非限制。尽管参照实施例对本发明进行了详细说明，本领域的普通技术人员应当理解，对本发明的技术方案进行修改或者等同替换，都不脱离本发明技术方案的精神和范围，其均应涵盖在本发明的权利要求范围当中。