一种基于二单元扫描干涉仪的自定标近场成像方法及其系统与流程
本发明属于被动微波遥感和近场目标探测与成像技术领域,具体地说,涉及一种基于二单元扫描干涉仪的自定标近场成像方法及其系统。
背景技术:
干涉式综合孔径辐射计是被动微波遥感领域中实现微波辐射测量的主要技术手段之一。该系统通过对观测场景亮温的空间频率域分布进行测量,获得可视度函数。然后利用观测场景亮温分布与可见度函数之间的傅里叶变换关系,重建观测场景的亮温分布。与传统真实孔径辐射计相比,干涉式综合孔径微波辐射计的最大优势在于解决了被动微波遥感空间分辨率低、机械扫描难度高以及体积重量大的技术问题,在星载对地观测领域受到越来越多的关注。2009年欧空局发射的土壤湿度与海洋盐度卫星(smos,soilmoistureandoceansalinity)是国际首颗以综合孔径微波辐射计为主载荷的对地观测卫星。在此之后,针对海洋盐度遥感及静止轨道大气探测等应用场景,多项新体制载荷概念及卫星观测计划相继提出,相关技术得到了迅速发展。除卫星遥感应用之外,近场成像是干涉式综合孔径技术的另一个重要应用领域。一方面,在地面测试阶段,面向星载应用所研发的综合孔径辐射计系统往往无法达到所需要的远场条件,必须在近场条件下,完成对系统成像及部分系统级指标的验证;另一方面,近年来,人体隐匿危险品安检成像、恶劣视觉条件下的近距离目标成像、地下埋入物品探测等方面的实际应用也对高分辨率被动微波近场成像提出了迫切的需求。
但是,传统的基于傅里叶变换的成像算法是在满足远场条件的前提之下,而在近场条件下,由于天线阵列到空间域采样点的距离差不一致引入的近场相位误差,导致该条件下的基于傅里叶变换的成像算法失效,因此,近场成像算法是综合孔径辐射计近距离成像应用亟待解决的关键问题。
国内外研究机构采用了不同的方法进行解决,第一类近场成像方法的思路是通过改变天线布局排列,使得可视度函数与亮温分布满足傅里叶变换关系,如新泽西理工学院和丹麦技术大学提出将球面分布的天线阵用于近场观测,从而得到与远场条件下相同的可视度函数表达式,进而利用傅里叶变换关系反演得到目标亮温。该方法的最大优势在于可实现对任意大小目标的近场观测,但是,该方法限制了系统的观测距离,其仅对球面半径距离处的场景的成像结果有效,若对其他距离处的目标进行探测,必须改变球面阵的半径长度,这在实际应用中很难实现,另外,傅立叶变换关系是在满足傍轴近似的前提条件下,即要求观测距离远大于所采用的天线阵型的最长基线,在探测天线与目标视场的距离较小的情况下,采用二阶近似不能够保证精度,直接利用傅立叶变换进行反演会使得成像结果出现较大误差。
另一类近场成像方法的思路是在原有的平面阵基础上,对近场条件下的可视度函数相位进行修正,使得场景亮温分布与可视度函数成为一种近似的傅里叶变换关系。如欧空局的smos卫星上搭载的有效载荷miras和美国nasa研制的地球静止轨道星载毫米波综合孔径辐射计geostar样机的地面成像测试中,采用了近场相位校正方法,对点源目标及扩展目标的测试数据进行了处理。其中,在对扩展目标进行成像实验时,研究人员以成像系统的天线阵的中心轴线的某一位置处作为参考点源,并假设系统探测数据是由该点源造成。但是,在某一位置存在一个参考点源的假设没有理论支撑,而且该方法对占据视场范围较大的扩展目标成像时误差较大。
张成等人提出了一种基于moore-penrose广义逆的面聚焦数值求解法,并利用一维天线阵型对点源和扩展目标进行了近场成像仿真和外场试验,该方法相比于相位修正傅里叶变换法的成像效果有明显改善,且不受观测距离的限制。但是,该方法对于二维天线阵型的反演来说,计算复杂度高,运算效率差。
陈建飞等人提出了一种基于g矩阵的正则化综合孔径近场成像算法并进行了针对一维和二维天线阵的仿真实验,该方法相比于传统的g矩阵算法更能有效的提高图像重建的精确度。相比于fft算法来说,正则化g矩阵方法成像误差相对较小,这是因为该方法直接利用正则化方法对原始可视度函数采样数据进行处理,且不需要插值。但是,该方法同样存在计算量和运算量较大的问题。
姚现勋等人提出了一种基于局部自适应偏微分方程的近场图像反演算法,该算法的基本原理是根据原始场景亮温图像的局部特征采用不同的算法,采用各向同性扩散抑制背景区域噪声,采用自适应扩散保持目标区域内边缘细节信息,该方案可有效降低可视度函数测量过程中所包含的噪声对图像反演的影响。但是,该方法仍未达到二维天线阵型快速成像的目的。
在国内外综合孔径辐射计的应用中,二维天线阵型的使用越来越广泛,但是,现阶段的近场成像方法均存在着成像速度慢,计算复杂度高的弊端。
二元干涉仪是干涉式综合孔径微波辐射计系统的最小组成单元,通过二元分时采样可构成各种阵列构型及其对应的基线组合采样覆盖,可用于近场成像系统及算法的原型验证。已有的近场成像方法是基于参考点源的误差整体校正方法,该方法可在距离信息未知的情况下,通过对目标平面中心处参考点源进行实际辅助测量获得近场相位的校正信息,从而同时完成对系统接收通道相位误差的校准。设二单元干涉仪对小太阳直接探测所得可视度函数为vf,对相同观测距离条件下的视场中心点源目标的直接探测所得可视度函数为vf0,则经该方法校正后的可视度函数vf′为:
但是,该方法针对不同观测距离的目标探测过程中,除对目标的一次成像外,还需对视场中心点源进行成像,试验过程较为繁琐。
对于二单元扫描干涉仪来说,所有可视度函数是用两个接收机分时采样获得,两通道间的相位差异导致所有可视度函数均存在一个相同的相位误差项。而现有的近场成像方法,是基于参考点源的近场成像方法,无法解决上述二单元扫描干涉仪存在的相位误差技术问题。
技术实现要素:
本发明的目的在于,为解决现有技术存在上述缺陷,本发明提出了一种基于二单元扫描干涉仪的自定标近场成像方法,一种将接收机通道相位误差和近场相位误差进行分步校正的自定标近场成像方法,基于近场待观测视场的二维亮温图像与近场误差校正后的可视度函数数据之间的傅里叶变换关系,以近场待观测视场的二维亮温图像为输入变量,利用近场误差校正后的可视度函数,采用快速逆傅里叶变换类算法反演出目标亮温,可大大简化计算复杂度,适于进行高速率视频成像,该方法不需要再对参考点源进行二次成像,大大简化了近场目标探测试验步骤。
本发明提供的一种基于二单元扫描干涉仪的自定标近场成像方法,所述二单元扫描干涉仪利用放置在水平和竖直两个方向的滑架上在对应的滑架上的移动产生不同基线,所有基线构成一个网格分布的点阵,等效于天线阵列构型;该方法包括:
利用两个天线单元进行分时采样,将两个接收机接收的采样数据进行复相关运算,获得与每一基线对应的可视度函数值,生成一个可视度函数值集合,作为可视度函数;
对获得的可视度函数进行接收机通道相位误差校正和近场相位误差校正,获得近场误差校正后的可视度函数;
基于近场待观测视场的二维亮温图像与近场误差校正后的可视度函数之间的傅里叶变换关系,以近场待观测视场的二维亮温图像为输入变量,利用近场误差校正后的可视度函数,根据不同的天线阵列构型,采用不同的快速逆傅里叶变换算法,进行图像反演,获得近场观测视场的亮温图像。
作为上述技术方案的改进之一,所述利用两个天线单元进行分时采样,将两个接收机接收的采样数据进行复相关运算,获得与每一基线对应的可视度函数值,生成一个可视度函数值集合,作为可视度函数;具体为:
将二单元扫描干涉仪中的两个接收机接收的采样数据进行复相关运算:
其中,v12为t时刻两个接收机接收的采样数据进行复相关运算后的与基线对应的可视度函数值;e1(d1,t)为其中一个接收机接收的采样数据;e2(d2,t)为另外一个接收机接收的采样数据;d1为一空间域采样点到其中一个天线单元的直线距离;d2为一空间域采样点到另外一个天线单元的直线距离;其中,所述采样数据为辐射场强;
根据二单元扫描干涉仪中的两个天线单元的分时采样,得到不同基线及其对应的可视度函数值,将每一条基线对应的可视度函数值进行汇总,生成一个可视度函数值集合,将其作为可视度函数vf,并进行存储。
作为上述技术方案的改进之一,所述对获得的可视度函数进行接收机通道相位误差校正和近场相位误差校正,获得近场误差校正后的可视度函数;具体为:
对获得的可视度函数进行接收机通道相位误差校正,得到经接收机通道相位误差校正后的可视度函数:
vf1=vf·e-j·a(1)
其中,a为接收机通道相位误差;j为虚数单位;e-j·a为通道相位误差补偿因子;vf1为经接收机通道相位误差校正后的可视度函数;
对经接收机通道相位误差校正后的可视度函数vf1进行近场相位误差校正,得到经近场相位误差校正后的可视度函数:
其中,vf2为经近场相位误差校正后的可视度函数;vf′0为视场中心点源目标可视度函数数据;angle(vf′0)为vf′0的相位;
其中,视场中心点源目标可视度函数数据为二单元扫描干涉仪在对视场中心点源观测场景的扫描过程中,得到的所有基线对应的可视度函数值的集合,即v12(u,v)的集合;其中,v12(u,v)计算公式为:
其中,tb(ξ,η)为视场中心点源目标的亮温值;(ξ,,η)为方向余弦坐标:
作为上述技术方案的改进之一,所述天线阵列构型为利用分别放置在水平和竖直两个方向的滑架上的天线单元在对应的滑架上的移动形成的运动轨迹;其包括:开环形二维天线阵列和闭环形二维天线阵列;
其中,开环形二维天线阵列包括:y形二维天线阵列、u形二维天线阵列和t形二维天线阵列;
闭环形二维天线阵列包括:圆环形二维天线阵列、六边形二维天线阵列和方形二维天线阵列。
作为上述技术方案的改进之一,所述根据不同的天线阵列构型,采用不同的快速逆傅里叶变换算法,进行图像反演,获得近场观测视场的亮温图像;具体为:
对于t形二维天线阵列、方形二维天线阵列和u形二维天线阵列,其空间频率域采样点呈矩形网格分布,直接采用ifft算法,进行图像反演,获得近场观测视场的亮温图像;
对于y形二维天线阵列和六边形二维天线阵列,其空间频率域采样点呈六边形网格分布,直接采用六边形ifft算法,进行图像反演,获得近场观测视场的亮温图像;
对于圆环形二维天线阵列,其空间频率域采样点呈圆形网格分布,采用伪极网格逆傅里叶算法,进行图像反演,获得近场观测视场的亮温图像。
本发明还提供了一种基于二单元扫描干涉仪的自定标近场成像系统,该系统包括:二单元扫描干涉仪、设置在水平和竖直两个方向上的滑架和设置在上位机上的可视度函数获取模块、可视度函数校正模块和图像反演模块;利用放置在水平和竖直两个方向的滑架上的二单元扫描干涉仪中的两个接收机在对应的滑架上的移动产生不同基线,所有基线构成一个网格分布的点阵,等效于天线阵列构型;
所述可视度函数获取模块,用于利用两个天线单元进行分时采样,将两个接收机接收的采样数据进行复相关运算,获得与每一基线对应的可视度函数值,生成一个可视度函数值集合,获得可视度函数;
所述可视度函数校正模块,用于对获得的可视度函数进行接收机通道相位误差校正和近场相位误差校正,获得近场误差校正后的可视度函数;
所述图像反演模块,用于基于近场待观测视场的二维亮温图像与近场误差校正后的可视度函数之间的傅里叶变换关系,以近场待观测视场的二维亮温图像为输入变量,利用近场误差校正后的可视度函数,根据不同的天线阵列构型,采用不同的快速逆傅里叶变换算法,进行图像反演,获得近场观测视场的亮温图像。
作为上述技术方案的改进之一,所述可视度函数获取模块,用于利用两个天线单元进行分时采样,将两个接收机接收的采样数据进行复相关运算,获得与每一基线对应的可视度函数值,生成一个可视度函数值集合,获得可视度函数;其具体过程为:
将二单元扫描干涉仪中的两个接收机接收的采样数据进行复相关运算:
其中,v12为t时刻两个接收机接收的采样数据进行复相关运算后的与基线对应的可视度函数值;e1(d1,t)为其中一个接收机接收的采样数据;e2(d2,t)为另外一个接收机接收的采样数据;d1为一空间域采样点到其中一个天线单元的直线距离;d2为一空间域采样点到另外一个天线单元的直线距离;其中,所述采样数据为辐射场强;
根据二单元扫描干涉仪中的两个天线单元的分时采样,得到不同基线及其对应的可视度函数值,将每一条基线对应的可视度函数值进行汇总,生成一个可视度函数值集合,将其作为可视度函数vf,并进行存储。
作为上述技术方案的改进之一,所述可视度函数校正模块,用于对获得的可视度函数进行接收机通道相位误差校正和近场相位误差校正,获得近场误差校正后的可视度函数;其具体过程为:
对获得的可视度函数进行接收机通道相位误差校正,得到经接收机通道相位误差校正后的可视度函数:
vf1=vf·e-j·a(1)
其中,a为接收机通道相位误差;j为虚数单位;e-j·a为通道相位误差补偿因子;vf1为经接收机通道相位误差校正后的可视度函数;
对经接收机通道相位误差校正后的可视度函数vf1进行近场相位误差校正,得到经近场相位误差校正后的可视度函数:
其中,vf2为经近场相位误差校正后的可视度函数;vf′0为视场中心点源目标可视度函数数据;angle(vf′0)为vf′0的相位;
其中,视场中心点源目标可视度函数数据为二单元扫描干涉仪在对视场中心点源观测场景的扫描过程中,得到的所有基线对应的可视度函数值的集合,即v12(u,v)的集合;其中,v12(u,v)计算公式为:
其中,tb(ξ,η)为视场中心点源目标的亮温值;(ξ,η)为方向余弦坐标:
作为上述技术方案的改进之一,所述天线阵列构型为利用分别放置在水平和竖直两个方向的滑架上的天线单元在对应的滑架上的移动形成的运动轨迹;其包括:开环形二维天线阵列和闭环形二维天线阵列;
其中,开环形二维天线阵列包括:y形二维天线阵列、u形二维天线阵列和t形二维天线阵列;
闭环形二维天线阵列包括:圆环形二维天线阵列、六边形二维天线阵列和方形二维天线阵列。
作为上述技术方案的改进之一,所述根据不同的天线阵列构型,采用不同的快速逆傅里叶变换算法,进行图像反演,获得近场观测视场的亮温图像;具体为:
对于t形二维天线阵列、方形二维天线阵列和u形二维天线阵列,其空间频率域采样点呈矩形网格分布,直接采用ifft算法,进行图像反演,获得近场观测视场的亮温图像;
对于y形二维天线阵列和六边形二维天线阵列,其空间频率域采样点呈六边形网格分布,直接采用六边形ifft算法,进行图像反演,获得近场观测视场的亮温图像;
对于圆环形二维天线阵列,其空间频率域采样点呈圆形网格分布,采用伪极网格逆傅里叶算法,进行图像反演,获得近场观测视场的亮温图像。
本发明与现有技术相比的有益效果是:
(1)成像速度快,可利用fft成像,计算复杂度低,而且不会像基于g矩阵的反演方法那样出现病态性,适合进行高速率视频成像。
(2)操作简单,相比g矩阵方法而言,不需已知目标的具体空间三维分布信息,仅需已知目标到阵列中心的距离信息;相比基于参考点源的成像方法而言,不需对参考点源进行二次成像,可大大简化近场目标探测试验步骤。
附图说明
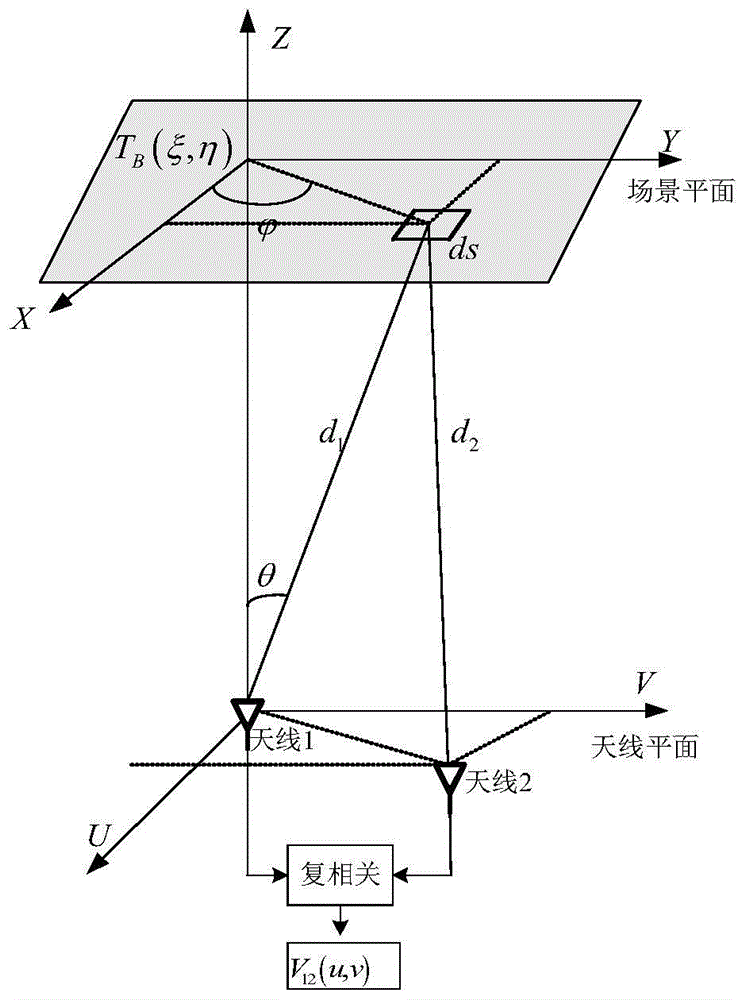
图1是本发明的一种基于二单元扫描干涉仪的自定标近场成像方法中的中心点源目标可视度函数数据的数据获取原理示意图;
图2是本发明的一种基于二单元扫描干涉仪的自定标近场成像方法的一个具体实施例中的二单元扫描干涉仪对暗室内取暖器目标的近场探测试验所得可视度函数相位示意图;
图3是图2的本发明的一种基于二单元扫描干涉仪的自定标近场成像方法的一个具体实施例中的基于近场探测试验所得可视度函数直接进行亮温重建的目标成像结果示意图;
图4是本发明的一种基于二单元扫描干涉仪的自定标近场成像方法中的经接收机通道相位误差校正后的可视度函数相位示意图;
图5是本发明的一种基于二单元扫描干涉仪的自定标近场成像方法中的经近场相位误差校正后的可视度函数相位示意图;
图6是本发明的一种基于二单元扫描干涉仪的自定标近场成像方法中利用近场误差校正后的可视度函数,对近场待观测视场的二维亮温图像进行反演,所得的目标亮温图像示意图;
图7是本发明的一种基于二单元扫描干涉仪的自定标近场成像方法的流程图。
具体实施方式
现结合附图对本发明作进一步的描述。
本发明提供了一种基于二单元扫描干涉仪的自定标近场成像方法,是针对二单元扫描干涉仪的近场探测;现有的成像方法是基于参考点源的近场成像方法,可在观测距离未知的情况下,同时完成对近场相位误差和系统接收通道误差的校准,但是,现有的方法在对不同距离的目标探测过程中,除对目标的一次探测外,还需对参考点源再次成像,试验过程较为繁琐。针对这一技术问题,本发明提出一种将系统通道相位误差、近场相位误差分步校正的自定标近场成像方法,基于近场待观测视场的二维亮温图像与近场误差校正后的可视度函数数据之间的傅里叶变换关系,以近场待观测视场的二维亮温图像为输入变量,利用近场误差校正后的可视度函数,采用快速逆傅里叶变换算法反演出目标亮温,,具有操作简单、成像速度快,计算复杂度低的优势。
本发明提供了一种基于二单元扫描干涉仪的自定标近场成像方法,如图7所示,该方法包括:
将二单元扫描干涉仪中的两个接收机接收的采样数据进行复相关运算,获得与基线对应的可视度函数值,根据二单元扫描干涉仪中的两个天线单元的分时采样,获得可视度函数,并进行存储;
具体地,将二单元扫描干涉仪中的两个接收机接收的采样数据进行复相关运算:
其中,v12为t时刻两个接收机接收的采样数据进行复相关运算后的与基线对应的可视度函数值;e1(d1,t)为其中一个接收机接收的采样数据;e2(d2,t)为另外一个接收机接收的采样数据;d1为一空间域采样点到其中一个天线单元的直线距离;d2为一空间域采样点到另外一个天线单元的直线距离;其中,所述采样数据为辐射场强;
根据二单元扫描干涉仪中的两个天线单元的分时采样,得到不同基线及其对应的可视度函数值,将每一条基线对应的可视度函数值进行汇总,生成一个可视度函数值集合,将其作为可视度函数vf,并进行存储。
对获得的可视度函数进行接收机通道相位误差校正和近场相位误差校正,获得近场误差校正后的可视度函数;
具体地,对获得的可视度函数进行接收机通道相位误差校正,得到经接收机通道相位误差校正后的可视度函数:
vf1=vf·e-j·a(1)
其中,a为接收机通道相位误差;j为虚数单位;e-j·a为通道相位误差补偿因子;vf1为经接收机通道相位误差校正后的可视度函数;vf为可视度函数;
由于经接收机通道相位误差校正后的可视度函数vf1仍然存在近场相位误差,因此,需要利用对视场中心点源目标的近场成像仿真实验所得的视场中心点源目标可视度函数数据vf′0,对经接收机通道相位误差校正后的可视度函数vf1进行近场相位误差校正,得到经近场相位误差校正后的可视度函数:
其中,vf2为经近场相位误差校正后的可视度函数;vf′0为视场中心点源目标可视度函数数据;angle(vf′0)为vf′0的相位;
其中,中心点源目标可视度函数数据的数据获取原理,如图1所示,视场中心点源目标所在的场景平面与天线1、天线2两个天线单元所在的天线平面平行,tb(ξ,η)为视场中心点源目标的亮温;(ξ,η)为方向余弦坐标;其中,
基于以上原理,利用matlab软件,构造天线阵列构型,使其对应的空间频率域覆盖形状与二单元扫描干涉仪获取的基线覆盖形状相同,在暂不考虑天线方向图误差的影响和已知目标观测距离的条件下,单个基线对整个视场中心点源目标所在的场景平面探测所得的可视度函数值v12(u,v)表示为:
其中,vf′0为在二单元干涉仪对视场中心点源观测场景的扫描过程中,所得所有基线对应的可视度函数值的集合,即v12(u,v)的集合。
基于近场待观测视场的二维亮温图像与近场误差校正后的可视度函数之间的傅里叶变换关系,利用经近场误差校正后的可视度函数vf2,根据不同的天线阵列构型,采用不同的快速逆傅里叶变换算法,进行图像反演,获得近场观测视场的亮温图像。
其中,所述不同天线阵列构型包括:开环形二维天线阵列和闭环形二维天线阵列;
其中,开环形二维天线阵列包括:y形二维天线阵列、u形二维天线阵列和t形二维天线阵列;
闭环形二维天线阵列包括:圆环形二维天线阵列、六边形二维天线阵列和方形二维天线阵列。
其中,对于t形二维天线阵列、方形二维天线阵列和u形二维天线阵列,其空间频率域采样点呈矩形网格分布,直接采用ifft算法,进行图像反演,获得近场观测视场的亮温图像;
对于y形二维天线阵列和六边形二维天线阵列,其空间频率域采样点呈六边形网格分布,直接采用六边形ifft算法,进行图像反演,获得近场观测视场的亮温图像;
对于圆环形二维天线阵列,其空间频率域采样点呈圆形网格分布,采用伪极网格逆傅里叶算法,进行图像反演,获得近场观测视场的亮温图像。
本发明还提供了一种基于二单元扫描干涉仪的自定标近场成像系统,该系统包括:二单元扫描干涉仪、设置在水平和竖直两个方向上的滑架和设置在上位机上的可视度函数获取模块、可视度函数校正模块和图像反演模块;利用放置在水平和竖直两个方向的滑架上的二单元扫描干涉仪中的两个接收机在对应的滑架上的移动产生不同基线,所有基线构成一个网格分布的点阵,等效于天线阵列构型;
可视度函数获取模块,用于利用两个天线单元进行分时采样,将两个接收机接收的采样数据进行复相关运算,获得与每一基线对应的可视度函数值,生成一个可视度函数值集合,获得可视度函数;
其具体过程为:
将二单元扫描干涉仪中的两个接收机接收的采样数据进行复相关运算:
其中,v12为t时刻两个接收机接收的采样数据进行复相关运算后的与基线对应的可视度函数值;e1(d1,t)为其中一个接收机接收的采样数据;e2(d2,t)为另外一个接收机接收的采样数据;d1为一空间域采样点到其中一个天线单元的直线距离;d2为一空间域采样点到另外一个天线单元的直线距离;其中,所述采样数据为辐射场强;
根据二单元扫描干涉仪中的两个天线单元的分时采样,得到不同基线及其对应的可视度函数值,将每一条基线对应的可视度函数值进行汇总,生成一个可视度函数值集合,将其作为可视度函数vf,并进行存储。
所述可视度函数校正模块,用于对获得的可视度函数进行接收机通道相位误差校正和近场相位误差校正,获得近场误差校正后的可视度函数;
其具体过程为:
对获得的可视度函数进行接收机通道相位误差校正,得到经接收机通道相位误差校正后的可视度函数:
vf1=vf·e-j·a(1)
其中,a为接收机通道相位误差;j为虚数单位;e-j·a为通道相位误差补偿因子;vf1为经接收机通道相位误差校正后的可视度函数;
对经接收机通道相位误差校正后的可视度函数vf1进行近场相位误差校正,得到经近场相位误差校正后的可视度函数:
其中,vf2为经近场相位误差校正后的可视度函数;vf0′为视场中心点源目标可视度函数数据;angle(vf′0)为vf′0的相位;
其中,视场中心点源目标可视度函数数据为二单元扫描干涉仪在对视场中心点源观测场景的扫描过程中,得到的所有基线对应的可视度函数值的集合,即v12(u,v)的集合;其中,v12(u,v)计算公式为:
其中,tb(ξ,η)为视场中心点源目标的亮温值;(ξ,η)为方向余弦坐标:
所述图像反演模块,用于基于近场待观测视场的二维亮温图像与近场误差校正后的可视度函数之间的傅里叶变换关系,以近场待观测视场的二维亮温图像为输入变量,利用近场误差校正后的可视度函数,根据不同的天线阵列构型,采用不同的快速逆傅里叶变换算法,进行图像反演,获得近场观测视场的亮温图像。
其中,所述天线阵列构型为利用分别放置在水平和竖直两个方向的滑架上的天线单元在对应的滑架上的移动形成的运动轨迹;其包括:开环形二维天线阵列和闭环形二维天线阵列;
其中,开环形二维天线阵列包括:y形二维天线阵列、u形二维天线阵列和t形二维天线阵列;
闭环形二维天线阵列包括:圆环形二维天线阵列、六边形二维天线阵列和方形二维天线阵列。
作为上述技术方案的改进之一,所述根据不同的天线阵列构型,采用不同的快速逆傅里叶变换算法,进行图像反演,获得近场观测视场的亮温图像;具体为:
对于t形二维天线阵列、方形二维天线阵列和u形二维天线阵列,其空间频率域采样点呈矩形网格分布,直接采用ifft算法,进行图像反演,获得近场观测视场的亮温图像;
对于y形二维天线阵列和六边形二维天线阵列,其空间频率域采样点呈六边形网格分布,直接采用六边形ifft算法,进行图像反演,获得近场观测视场的亮温图像;
对于圆环形二维天线阵列,其空间频率域采样点呈圆形网格分布,采用伪极网格逆傅里叶算法,进行图像反演,获得近场观测视场的亮温图像。
实施例1.
本实例中的二单元扫描干涉仪利用放置在水平和竖直两个方向滑架上的接收机在滑架上的移动产生不同基线,所有的基线构成一个矩形网格分布的点阵,等效于t型天线阵列的采样效果。
下面利用该二单元干涉仪开展了近场目标成像试验。利用该二单元干涉仪对暗室内观测距离为5.5m的小太阳(取暖器)进行探测,利用两个接收机对两个天线单元接收的采样数据进行复相关运算,得到包含有不同的基线对应的可视度函数值的可视度函数vf,v=0对应的vf的相位如图2所示。基于可视度函数vf重建的亮温图像结果,如图3所示。
从图2中可以明显看出,由于接收机通道相位误差和近场相位误差的存在,取暖器在近场条件下,探测所得的可视度函数相位在最短基线处有一定偏移且不满足共轭对称关系;因此,造成了图3所示的亮温图像重建结果不理想。
将最短基线处可视度函数相位近似作为接收机通道相位误差,即a近似为-1.496,经vf1=vf·e-j-a校正后的可视度函数相位如图4所示。对比图2和图4结果可以看出,经通道相位误差校正后的可视度函数相位在(u,v)=(0,0)处趋近于0。
利用matlab软件,构造t型天线阵列,使其对应的空间频率域覆盖形状与二单元扫描干涉仪获取的基线覆盖形状相同,在暂不考虑天线方向图误差的影响和已知观测距离为5.5m的条件下,以视场中心点源目标为探测目标,单个基线对整个观测视场探测所得的可视度函数值v12(u,v)表示为:
vf′0为视场中心点源目标可视度函数数据,即在二单元干涉仪对视场中心点源观测场景的扫描过程中,得到的所有基线对应的可视度函数值的集合,即v12(u,v)的集合;
基于视场中心点源目标可视度函数数据vf0′,根据:
对vf1进行近场相位误差校正,得到经近场相位误差校正的可视度函数vf2,校正后的可视度函数相位,如图5所示,此时,经过近场相位误差校正后的可视度函数相位近似满足共轭对称关系。
由于该实例中的基线分布为矩形网格分布,因此,可直接采用ifft算法,对经近场误差校正后的可视度函数vf2进行图像反演,获得近场观测视场的亮温图像,则重建后的亮温图像结果如图6所示。
将图6和直接成像结果图3对比可以发现,探测目标-小太阳的轮廓和形状更加清晰可辨识,从而验证了上述自定标近场成像方法的有效性,从而说明了本发明的方法具有操作简单、成像速度快,计算复杂度低的优点。
二单元干涉仪是干涉式综合孔径微波辐射计系统的最小组成单元,通过二元分时采样可构成一定范围覆盖的基线组合,可用于近场成像系统及算法的原型验证。现有的基于参考点源的误差整体校正方法,在针对不同观测距离的目标探测过程中,除对目标的一次成像外,还需对视场中心点源进行成像,试验过程较为繁琐。本发明提出的自定标近场成像方法,避免了对参考点源的成像试验,操作简单,可大大简化试验步骤,而且该方法的成像速度快,可利用ifft成像,计算复杂度低,而且不会像基于g矩阵的反演方法那样出现病态性,适合进行高速率视频成像。
最后所应说明的是,以上实施例仅用以说明本发明的技术方案而非限制。尽管参照实施例对本发明进行了详细说明,本领域的普通技术人员应当理解,对本发明的技术方案进行修改或者等同替换,都不脱离本发明技术方案的精神和范围,其均应涵盖在本发明的权利要求范围当中。
- 还没有人留言评论。精彩留言会获得点赞!