一种自适应基波消除方法与流程

本发明属于电机故障诊断技术领域，具体涉及一种自适应基波消除方法。

背景技术：

随着2015年5月由国务院印发的部署全面推进实施制造强国《中国制造2025》的战略文件的签批，我国对现代工业技术的发展和设备的制造水平提出了越来越高的要求，同时也对工厂生产过程中的智能化水平和生产过程的稳定运行级别提出了更高的要求。而异步电动机占国民生产中70％以上的电机比例，作为生产过程中的最底层执行元件，其是否能够正常运行，极大程度的反映和制约着生产制造过程中是否能够安全、高效、优质和低耗运行。该执行机构的损坏不仅影响电机本身，而且会影响整个生产系统的正常运行，甚至危及人身安全，造成巨大的经济损失和恶劣的社会影响。

对异步电机状态的实时监测和诊断对提高生产运行过程的稳定性、高效性、安全性等提供了保证，降低了维修成本和巡检成本，提高了运行效率，减少了突发事故造成的设备、材料和人员损失。因此异步电动机的故障实时在线诊断对工业生产起着重要的积极作用。

但是，申请人发现：目前对于异步电动机的诊断主要集中在大型的异步电动机，诊断的方式主要采用振动和温度信号，而电流诊断作为一种易融入的、非浸入式的、包含大量信息的、可在线的实时诊断方式，当前已成为社会各界学者和用户研究和关注的热点。同时也由于电流诊断的方式包含信息量大，反应问题多，从而对准备分析故障部位信息带来问题，即同一电流表征信息有可能反应同一电机不同问题，从而使得如何通过获取信息进行综合评估，获得具体故障信息成为了当前研究的热点问题。而电流分析的方法中不可避免的要利用频谱转换的过程，其基于快速傅里叶等转换的分辨率对采集的时间长短有严格的要求，采样时长对频谱转换的分辨率具有一定的制约性。而由于异步电动机的转差较小，尤其是电机处于轻载或空载时，转子断条故障等信息可能掩埋在基波频谱的泄漏现象中，而无法识别和准备辨识。

技术实现要素：

为解决现有技术中存在的上述问题，本发明提供了一种可从整体估计和分布估计分析获取在自适应消除基波波形的过程中转子故障信息或负载变化信息，并在时域对基波信号进行辨识和抵消，有效的消除基频信息的自适应基波消除方法。

为解决上述技术问题，本发明采用如下技术方案：

一种自适应基波消除方法，包括从整体估计的自适应辨识和补偿方法和从分布估计的自适应和补偿方法；其中，

所述从整体估计的自适应辨识和补偿方法为：首先在实时采集数据中截取数据量为n的数据，并根据最小二乘算法，计算其基波频率拟合曲线，然后通过实时数据和拟合基波数据，重构时域波形，最后通过对重构时域波形的频谱分析获取转子故障信息或负载变化信息；

所述从分布估计的自适应和补偿方法为：首先在实时采集数据中截取数据量为m个fs/50的数据，并根据最小二乘算法，计算其基波频率拟合曲线，然后通过实时数据和拟合基波数据，重构区域时域波形，再将区域时域波形进行时间序列排序，最后通过对重构时域波形的频谱分析获取转子故障信息或负载变化信息。

进一步地，所述从整体估计的自适应辨识和补偿方法，具体包括以下步骤：

a1.利用霍尔电流传感器和数据采集卡获取n+m个实时电流数据；

a2.在n+m个实时电流数据上截取n个数据记为yn；

a3.假设y’n为拟合的n个实时数据的基波数据,利用最小均方误差，逼近待提取信号，计算得到y’n；

a4.利用估计基波时间序列数据，补偿实时获取电流数据，重构时间序列数据△yn(k)，即△yn(k)＝yn(k)-y’n(k)，k＝1,2…n；

a5.利用最小均方误差，重构逼近时间序列数据△yn(k)的拟合曲线△y’n(k)；

a6.根据△w对步骤a4中拟合的基波时间序列数据y’n(k)进行重修正，其中，△w＝|ω1-ω2|，ω1为拟合的时间序列y’n(k)的频率，ω2为△yn(k)的拟合曲线△y’n(k)的频率；

a7.利用快速傅里叶变化，获取修正后时间序列数据△yn(k)的频谱图，并从频谱图中分析获取转子故障信息或负载变化信息。

进一步地，步骤a1的采样频率fs为10khz，采样时间t为0.0001s。

进一步地，步骤a3中利用最小均方误差，逼近待提取信号,计算得到y'n，具体为：通过公式e(e²y)＝(yn-y’n)²＝min和公式y’n＝a(ω1t+θ1)，计算得到y'n，其中e(e²y)为yn与y’n差值的平方，eyn为yn-y’n的时间序列误差，a(ω1t+θ1)为y’n用三角函数表示时的公式，ω1为y’n的角速度，它表示了周期信号时间轴的伸缩情况，t为时间变量，θ1为y’n周期信号的初始相位；

步骤a5利用最小均方误差，重构逼近时间序列数据△yn(k)的拟合曲线△y’n(k)，具体为：通过公式e(e²△yn)＝(△yn(k)-△y’n(k))²＝min和e△yn＝＝bsin(ω2t+θ2)，计算得到时间序列数据△yn(k)的拟合曲线△y’n(k)，其中e(e²△yn)为△yn(k)与△y’n(k)差值的平方，e△yn为△yn(k)-△y’n(k)的时间序列误差，bsin(ω2t+θ2)为e(e²△yn)用三角函数表示时的公式，ω2为e(e²△yn)的角速度，它表示了周期信号时间轴的伸缩情况，t为时间变量，θ2为e(e²△yn)周期信号的初始相位。

进一步地，步聚a6中根据△w对步骤a4中估计的基波时间序列数据进行重修正，具体为：当△w<0.1,判断△a,△a＝b/a，△a>0.01，基波时间序列数据修正为△yn(k)＝yn(k)-y’n(k)-e△y(k)，k＝1,2…n；当△w>＝0.1π,基波时间序列数据修正为△yn(k)＝yn(k)-y’n(k)，k＝1,2…n；其中a为y’n的最大幅值，b为e(e²△yn)的最大幅值。

进一步地，所述从分布估计的自适应和补偿方法，具体包括以下步骤：

b1.利用霍尔电流传感器和数据采集卡获取n+m个实时电流数据；

b2.在n+m个实时电流数据上截取k个fs/50个数据记为ym；

b3.假设y’m为第m个拟合的个实时数据ym的基波数据，利用最小均方误差，逼近待提取信号，计算得到y’m，其中m＝1、2…k，表示需要循环计算k次；

b4.利用估计的基波时间序列数据，补偿实时获取电流数据，求取重构差值数据△ym(z)，即△ym(z)＝ym(z)-y’m(z)，z＝1,2…fs/50；

b5.利用最小均方误差，重构差值数据△ym(z)的拟合曲线△y’m(z)；

b6.根据△w，对步骤b4中估计的基波周期数据进行重修正，其中△w＝|ω1-ω2|，其中ω1为y’n的角速度，它表示了周期信号时间轴的伸缩情况，ω2为e(e²△yn)的角速度，它表示了周期信号时间轴的伸缩情况；

b7.按顺序对修正后差值数据△y1(z)、△y2(z)…△ym(z)进行时间轴数据的重构，重构数据记为△y；

b8.利用快速傅里叶变化，获取重构数据△y的频谱图，并从频谱图中分析获取转子故障信息或负载变化信息。

进一步地，步骤b1的采样频率fs为10khz，采样时间t为0.0001s。

进一步地，步骤b3中利用最小均方误差，逼近待提取信号，计算得到y’m，具体为：通过公式e(e²y)＝(ym-y’m)²＝min和y’m＝a(ω1t+θ1)，计算得到y’m；其中e(e²ym)为ym与y’m差值的平方，a(ω1t+θ1)为e(e²ym)的三角函数表示公式，ω1为e(e²ym)的角速度，它表示了周期信号时间轴的伸缩情况，t为时间变量，θ1为e(e²△yn)周期信号的初始相位；

步骤b5中利用最小均方误差，重构差值数据△ym(z)的拟合曲线△y’m(z)，具体为：通过公式e(e²△ym)＝(△ym(z)-△y’m(z))²＝min和公式e△ym＝＝bsin(ω2t+θ2)，计算得到△ym(z)的拟合曲线△y’m(z)，其中e(e²△ym)为的三角函数表示公式，bsin(ω2t+θ2)为e(e²△ym)的三角函数表示公式，ω2为角速度，它表示了周期信号时间轴的伸缩情况，t为时间变量，θ2为e(e²△ym)周期信号的初始相位。

进一步地，步骤b6中根据△w，对步骤b4中估计的基波周期数据进行重修正,具体为：当△w<0.1π,判断△a,△a＝b/a，△a>0.01，基波周期数据修正为△ym(z)＝ym(z)-y’n(z)-e△y(z)，z＝1,2…fs/50；当△w>＝0.1π,基波周期数据修正为△ym(z)＝ym(z)-y’m(z)，z＝1,2…fs/50；其中a为y’m的最大幅值，b为e(e²△ym)的最大幅值。

本发明主要具有以下有益效果：

本发明通过采用上述技术方案，即可从整体估计和分布估计分析获取在自适应消除基波波形的过程中转子故障信息或负载变化信息，并通过在时域对基波信号进行辨识和抵消，实现自适应辨识和补偿，有效的消除基频信息。

附图说明

图1是本发明实施例所述一种自适应基波消除方法中从整体估计的自适应辨识和补偿方法的流程示意图；

图2是本发明实施例所述一种自适应基波消除方法中从分布估计的自适应辨识和补偿方法的流程示意图；

图3是本发明实施例所述一种自适应基波消除方法中从整体估计的自适应辨识和补偿过程的示意图；

图4是本发明实施例所述一种自适应基波消除方法中从分布估计的自适应辨识和补偿过程的示意图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。

一种自适应基波消除方法，包括从整体估计的自适应辨识和补偿方法和从分布估计的自适应和补偿方法。其中，

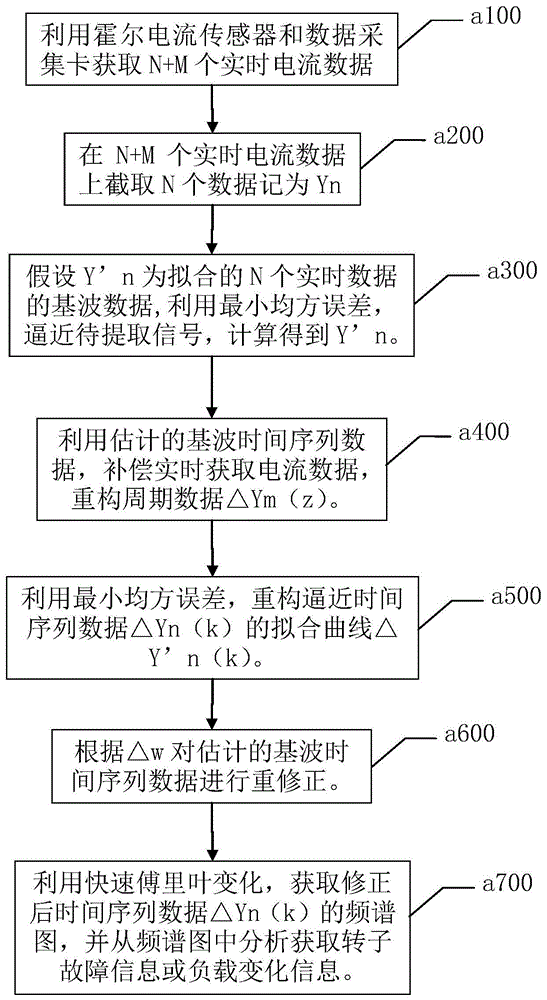
所述从整体估计的自适应辨识和补偿方法为：首先在实时采集数据中截取数据量为n的数据，并根据最小二乘算法，计算其基波频率拟合曲线，然后通过实时数据和拟合基波数据，重构时域波形，最后通过对重构时域波形的频谱分析获取转子故障信息或负载变化信息；如图1，具体包括以下步骤：

步骤a100.利用霍尔电流传感器和数据采集卡获取n+m个实时电流数据，采样频率fs优选为10khz，采样时间t优选为0.0001s；

步骤a200.在n+m个实时电流数据上截取n个数据记为yn；

步骤a300.假设y’n为拟合的n个实时数据的基波数据,利用最小均方误差，逼近待提取信号，计算得到y’n；具体为：通过公式e(e²y)＝(yn-y’n)²＝min和公式y’n＝a(ω1t+θ1)，计算得到y'n，其中e(e²y)为yn与y’n差值的平方，eyn为yn-y’n的时间序列误差，a(ω1t+θ1)为y’n用三角函数表示时的公式，ω1为y’n的角速度，它表示了周期信号时间轴的伸缩情况，t为时间变量，θ1为y’n周期信号的初始相位；

步骤a400.利用估计基波时间序列数据，补偿实时获取电流数据，重构时间序列数据△yn(k)，即△yn(k)＝yn(k)-y’n(k)，k＝1,2…n；

步骤a500.利用最小均方误差，重构逼近时间序列数据△yn(k)的拟合曲线△y’n(k)；通过公式e(e²△y)＝(△yn(k)-△y’n(k))²＝min和e△y＝＝bsin(ω2t+θ2)，计算得到时间序列数据△yn(k)的拟合曲线△y’n(k)，具体为：通过公式e(e²△yn)＝(△yn(k)-△y’n(k))²＝min和e△yn＝＝bsin(ω2t+θ2)，计算得到△yn(k)的拟合曲线△y’n(k)，其中e(e²△yn)为△yn(k)与△y’n(k)差值的平方，e△yn为△yn(k)-△y’n(k)的时间序列误差，bsin(ω2t+θ2)为e(e²△yn)用三角函数表示时的公式，ω2为e(e²△yn)的角速度，它表示了周期信号时间轴的伸缩情况，t为时间变量，θ2为e(e²△yn)周期信号的初始相位；

步骤a600.根据△w对步骤a4中估计的基波时间序列数据进行重修正，其中，△w＝|ω1-ω2|，ω1为拟合的时间序列y’n(k)的频率，ω2为△yn(k)的拟合曲线△y’n(k)的频率；具体为：当△w<0.1,判断△a,△a＝b/a，△a>0.01，基波时间序列数据修正为△yn(k)＝yn(k)-y’n(k)-e△y(k)，k＝1,2…n；当△w>＝0.1π,基波时间序列数据修正为△yn(k)＝yn(k)-y’n(k)，k＝1,2…n；其中a为y’n的最大幅值，b为e(e²△yn)的最大幅值；

步骤a700.利用快速傅里叶变化，获取修正后时间序列数据△yn(k)的频谱图，并从频谱图中分析获取转子故障信息或负载变化信息。

所述从分布估计的自适应和补偿方法为：首先在实时采集数据中截取数据量为m个fs/50的数据，并根据最小二乘算法，计算其基波频率拟合曲线，然后通过实时数据和拟合基波数据，重构区域时域波形，再将区域时域波形进行时间序列排序，最后通过对重构时域波形的频谱分析获取转子故障信息或负载变化信息；如图2，具体包括以下步骤：

步骤b100.利用霍尔电流传感器和数据采集卡获取n+m个实时电流数据，采样频率fs优选为10khz，采样时间t优选为0.0001s；

步骤b200.在n+m个实时电流数据上截取k个fs/50个数据记为ym；

步骤b300.假设y’m为第m个拟合的个实时数据ym的基波数据，利用最小均方误差，逼近待提取信号，计算得到y’m，其中m＝1、2…k，表示需要循环计算k次；具体为：通过公式e(e²y)＝(ym-y’m)²＝min和y’m＝a(ω1t+θ1)，计算得到y’m；其中e(e²ym)为ym与y’m差值的平方，a(ω1t+θ1)为e(e²ym)的三角函数表示公式，ω1为e(e²ym)的角速度，它表示了周期信号时间轴的伸缩情况，t为时间变量，θ1为e(e²△yn)周期信号的初始相位；

步骤b400.利用估计的基波时间序列数据，补偿实时获取电流数据，求取重构差值数据△ym(z)，即△ym(z)＝ym(z)-y’m(z)，z＝1,2…fs/50，重构△ym(z)的基波周期数据；

步骤b500.利用最小均方误差，重构差值数据△ym(z)的拟合曲线△y’m(z)，该重构的拟合曲线△y’m(z)是一个周期信号；具体为：通过公式e(e²△y)＝(△ym(z)-△y’m(z))²＝min和公式e△y＝＝bsin(ω2t+θ2)，计算得到y’m，其中e(e²△ym)为的三角函数表示公式，bsin(ω2t+θ2)为e(e²△ym)的三角函数表示公式，ω2为角速度，它表示了周期信号时间轴的伸缩情况，t为时间变量，θ2为e(e²△ym)周期信号的初始相位；

步骤b600.根据△w，对步骤b4中估计的基波周期数据进行重修正，其中△w＝|ω1-ω2|；具体为：当△w<0.1π,判断△a,△a＝b/a，△a>0.01，基波周期数据修正为△ym(z)＝ym(z)-y’n(z)-e△y(z)，z＝1,2…fs/50；当△w>＝0.1π,基波周期数据修正为△ym(z)＝ym(z)-y’m(z)，z＝1,2…fs/50；其中ω1为y’n的角速度，它表示了周期信号时间轴的伸缩情况，ω2为e(e²△yn)的角速度，它表示了周期信号时间轴的伸缩情况，a为y’m的最大幅值，b为e(e²△ym)的最大幅值；

步骤b700.按顺序对修正后差值数据△y1(z)、△y2(z)…△ym(z)进行时间轴数据的重构，重构数据记为△y；

步骤b800.利用快速傅里叶变化，获取重构数据△y的频谱图，并从频谱图中分析获取转子故障信息或负载变化信息。

本发明所述的自适应基波消除方法针对电机故障诊断过程中负载变化引起的特征信息频率或转子断条引起的故障特征频率信息由于快速傅里叶变化采集时间的局限性，易被掩埋在基频频率转化过程中的的泄漏现象中，分别从整体估计和分布估计两个方面出发，设计了两种可自适应的实时调整的消除基频波形的新方法。该方法在自适应消除基波波形的过程中，考虑了实时电源电压基波变化引起的电流基波波形变化信息，可以有效的消除基频信息。

以上所述是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也视为本发明的保护范围。