一种电力系统中谐波和间谐波的测量方法及装置与流程
本申请涉及电能质量技术领域,特别涉及一种电力系统中谐波和间谐波的测量方法及装置。
背景技术:
由于电力系统中广泛应用的各类负载装置很多都是波动的,因此波动负载产生的间谐波污染问题日益加剧。间谐波会放大电压闪变和音频干扰,影响传输画面及增大噪音,缩短电力系统中相关设备的使用寿命,增加电力线路的能耗,严重影响电能质量,因此对间谐波进行准确地检测和分析有着重要的意义。
电力系统的谐波分析通常是采用快速傅里叶变换的方法,但由于间谐波非工频整数倍,因此测量含有间谐波的信号时通常会出现频谱泄露。为了降低频谱泄露对谐波和间谐波测量精度的影响,现有技术一般会采用在时域加窗函数的方法来降低频谱泄露,并在此基础上采用插值修正的方法来测量。在时域加窗函数的过程中,一般通过增加频域窗函数主瓣的宽度来降低旁瓣的衰减度,但是窗函数主瓣宽度的增加会导致频率相近的谐波与间谐波之间的频谱发生重叠干涉,产生主瓣干扰,难以区分电信号中的谐波和间谐波,进而导致插值修正方法很难对谐波和间谐波进行准确地测量。
基于此,目前亟需一种电力系统中谐波和间谐波的测量方法,用于解决现有技术容易出现主瓣干扰,导致难以区分电力系统中电信号的谐波和间谐波,进而导致很难对谐波和间谐波进行准确地测量的问题。
技术实现要素:
本申请提供了一种电力系统中谐波和间谐波的测量方法及装置,可用于解决现有技术容易出现主瓣干扰,导致难以区分电力系统中电信号的谐波和间谐波,进而导致很难对谐波和间谐波进行准确地测量的技术问题。
第一方面,本申请实施例提供一种电力系统中谐波和间谐波的测量方法,所述方法包括:
获取电力系统中待测量的电信号,所述电信号包括x个谐波信号和y个间谐波信号;
对所述待测量电信号进行采样、加高斯窗处理以后,再进行快速离散傅里叶变换,生成信号频谱;所述信号频谱包括p个波峰,p=2(x+y);
根据所述波峰的数量,构造p个高斯径向基函数;
根据所述p个高斯径向基函数,得到待训练的目标函数;
对所述信号频谱进行处理,得到处理后的信号频谱;所述处理包括抽选、搬移和实部、虚部提取;
对所述待训练的目标函数进行迭代训练,使得所述待训练的目标函数逼近所述处理后的信号频谱,得到训练后的目标函数;
根据所述训练后的目标函数对应的参数,对谐波信号和间谐波信号分别进行测量。
在第一方面的一种可实现方式中,对所述待测量电信号进行采样、加高斯窗处理以后,再进行快速离散傅里叶变换,生成信号频谱,包括:
对所述待测量电信号进行采样、加高斯窗处理以后,再进行快速离散傅里叶变换,得到快速离散傅里叶变换后的信号点;
根据所述快速离散傅里叶变换后的信号点,生成信号频谱。
在第一方面的一种可实现方式中,所述快速离散傅里叶变换后的信号点通过以下公式确定:
其中,pw(n)为所述快速离散傅里叶变换后的信号点,n是信号点,k为整数,m为所述待测量电信号中谐波和间谐波个数的总和,ak为所述待测量电信号中任一谐波或间谐波的幅值,n取偶数,表示加高斯窗后信号点的数量;fk为所述待测量电信号中任一谐波或间谐波的频率,fs为采样频率,
在第一方面的一种可实现方式中,根据所述p个高斯径向基函数,得到待训练的目标函数,包括:
对所述p个高斯径向基函数进行加权求和,得到待训练的目标函数。
在第一方面的一种可实现方式中,所述待训练的目标函数通过以下公式表示:
其中,φi为所述p个高斯径向基函数中的任意一个,ε为高斯窗的形状参数,α为高斯窗参数,n取偶数,表示加高斯窗后信号点的数量;nf为频率取值的数据集合,t为窗函数宽度,fi为所述p个高斯径向基函数中的任意一个的频率中心,z为整数,
在第一方面的一种可实现方式中,对所述信号频谱进行处理,得到处理后的信号频谱;所述处理包括抽选、搬移和实部、虚部提取,包括:
对所述信号频谱进行抽选、搬移,得到整理后的信号频谱;
对所述整理后的信号频谱进行实部提取,得到整理后的信号实部频谱;
对所述整理后的信号频谱进行虚部提取,得到整理后的信号虚部频谱;
将整理后的信号实部频谱和整理后的信号虚部频谱共同作为所述处理后的信号频谱。
在第一方面的一种可实现方式中,所述整理后的信号实部频谱对应的函数和所述整理后的信号虚部频谱对应的函数通过以下公式确定:
r_pws(n)=real[pws(n)]
i_pws(n)=imag[pws(n)]
其中,pws(n)为所述整理后的信号频谱对应的信号点,r_pws(n)为所述整理后的信号实部频谱对应的函数,i_pws(n)为所述整理后的信号虚部频谱对应的函数,real表示取实部的运算,imag表示取虚部的运算。
在第一方面的一种可实现方式中,对所述待训练的目标函数进行迭代训练,使得所述待训练的目标函数逼近所述处理后的信号频谱,得到训练后的目标函数,包括:
根据所述待训练的目标函数和所述整理后的信号实部频谱对应的函数,确定第一损失函数;
利用梯度下降法对待训练的目标函数对应的频率中心和待训练的目标函数对应的权值进行训练,使得所述第一损失函数达到最小值,确定训练后的目标函数对应的频率中心和训练后的目标函数对应的权值;
将所述训练后的目标函数对应的频率中心和训练后的目标函数对应的权值代入所述待训练的目标函数,确定训练后的第一子函数;
将所述训练后的目标函数对应的频率中心代入所述待训练的目标函数,得到待训练的中间函数;
根据所述待训练的中间函数和所述整理后的信号虚部频谱对应的函数,确定第二损失函数;
利用梯度下降法对所述待训练的中间函数对应的权值进行训练,使得所述第二损失函数达到最小值,确定训练后的中间函数对应的权值;
将所述训练后的中间函数对应的权值代入所述待训练的中间函数,确定训练后的第二子函数;
将所述训练后的第一子函数和所述训练后的第二子函数共同作为所述训练后的目标函数。
在第一方面的一种可实现方式中,所述训练后的目标函数对应的参数包括所述训练后的第一子函数对应的频率中心、所述训练后的第一子函数对应的权值、所述训练后的第二子函数对应的权值;
所述待测量电信号中谐波的频率或间谐波的频率通过以下方式确定:
其中,f′0为所述待测量电信号中谐波的频率和间谐波的频率组成的向量,fm+1~f2m为所述待测量电信号经快速离散傅里叶变换后,生成的信号频谱中正频率部分对应的任一谐波或间谐波的频率,f0为所述训练后的第一子函数对应的频率中心,m为所述待测量电信号中谐波和间谐波个数的总和;
所述待测量电信号中谐波的幅值或间谐波的幅值通过以下公式确定:
其中,a’为所述待测量电信号中谐波的幅值和间谐波的幅值组成的向量,am+1~a2m为所述待测量电信号经快速离散傅里叶变换后,生成的信号频谱中正频率部分对应的任一谐波或间谐波的幅值,a为根据所述训练后的第一子函数对应的权值和所述训练后的第二子函数对应的权值计算出的幅值向量,m为所述待测量电信号中谐波和间谐波个数的总和,α为高斯窗参数,λr为所述训练后的第一子函数对应的权值,λi为所述训练后的第二子函数对应的权值,j为虚数单位,||表示取绝对值;
所述待测量电信号中谐波的相位或间谐波的相位通过以下公式确定:
其中,
第二方面,本申请实施例提供一种电力系统中谐波和间谐波的测量装置,所述装置包括:
获取单元,用于获取电力系统中待测量的电信号,所述电信号包括x个谐波信号和y个间谐波信号;
处理单元,用于对所述待测量电信号进行采样、加高斯窗处理以后,再进行快速离散傅里叶变换,生成信号频谱;所述信号频谱包括p个波峰,p=2(x+y);以及,根据所述波峰的数量,构造p个高斯径向基函数;以及,根据所述p个高斯径向基函数,得到待训练的目标函数;以及,对所述信号频谱进行处理,得到处理后的信号频谱;所述处理包括抽选、搬移和实部、虚部提取;以及,对所述待训练的目标函数进行迭代训练,使得所述待训练的目标函数逼近所述处理后的信号频谱,得到训练后的目标函数;
测量单元,用于根据所述训练后的目标函数对应的参数,对谐波信号和间谐波信号分别进行测量。
在第二方面的一种可实现方式中,所述处理单元具体用于:
对所述待测量电信号进行采样、加高斯窗处理以后,再进行快速离散傅里叶变换,得到快速离散傅里叶变换后的信号点;以及,根据所述快速离散傅里叶变换后的信号点,生成信号频谱。
在第二方面的一种可实现方式中,所述快速离散傅里叶变换后的信号点通过以下公式确定:
其中,pw(n)为所述快速离散傅里叶变换后的信号点,n是信号点,k为整数,m为所述待测量电信号中谐波和间谐波个数的总和,ak为所述待测量电信号中任一谐波或间谐波的幅值,n取偶数,表示加高斯窗后信号点的数量;fk为所述待测量电信号中任一谐波或间谐波的频率,fs为采样频率,
在第二方面的一种可实现方式中,所述处理单元具体用于:
对所述p个高斯径向基函数进行加权求和,得到待训练的目标函数。
在第二方面的一种可实现方式中,所述待训练的目标函数通过以下公式表示:
其中,φi为所述p个高斯径向基函数中的任意一个,ε为高斯窗的形状参数,α为高斯窗参数,n取偶数,表示加高斯窗后信号点的数量;nf为频率取值的数据集合,t为窗函数宽度,fi为所述p个高斯径向基函数中的任意一个的频率中心,z为整数,
在第二方面的一种可实现方式中,所述处理单元具体用于:
对所述信号频谱进行抽选、搬移,得到整理后的信号频谱;以及,对所述整理后的信号频谱进行实部提取,得到整理后的信号实部频谱;以及,对所述整理后的信号频谱进行虚部提取,得到整理后的信号虚部频谱;以及,将整理后的信号实部频谱和整理后的信号虚部频谱共同作为所述处理后的信号频谱。
在第二方面的一种可实现方式中,所述整理后的信号实部频谱对应的函数和所述整理后的信号虚部频谱对应的函数通过以下公式确定:
r_pws(n)=real[pws(n)]
i_pws(n)=imag[pws(n)]
其中,pws(n)为所述整理后的信号频谱对应的信号点,r_pws(n)为所述整理后的信号实部频谱对应的函数,i_pws(n)为所述整理后的信号虚部频谱对应的函数,real表示取实部的运算,imag表示取虚部的运算。
在第二方面的一种可实现方式中,所述处理单元具体用于:
根据所述待训练的目标函数和所述整理后的信号实部频谱对应的函数,确定第一损失函数;以及,利用梯度下降法对待训练的目标函数对应的频率中心和待训练的目标函数对应的权值进行训练,使得所述第一损失函数达到最小值,确定训练后的目标函数对应的频率中心和训练后的目标函数对应的权值;以及,将所述训练后的目标函数对应的频率中心和训练后的目标函数对应的权值代入所述待训练的目标函数,确定训练后的第一子函数;以及,将所述训练后的目标函数对应的频率中心代入所述待训练的目标函数,得到待训练的中间函数;以及,根据所述待训练的中间函数和所述整理后的信号虚部频谱对应的函数,确定第二损失函数;以及,利用梯度下降法对所述待训练的中间函数对应的权值进行训练,使得所述第二损失函数达到最小值,确定训练后的中间函数对应的权值;以及,将所述训练后的中间函数对应的权值代入所述待训练的中间函数,确定训练后的第二子函数;以及,将所述训练后的第一子函数和所述训练后的第二子函数共同作为所述训练后的目标函数。
在第二方面的一种可实现方式中,所述训练后的目标函数对应的参数包括所述训练后的第一子函数对应的频率中心、所述训练后的第一子函数对应的权值、所述训练后的第二子函数对应的权值;所述待测量电信号中谐波的频率或间谐波的频率通过以下方式确定:
其中,f′0为所述待测量电信号中谐波的频率和间谐波的频率组成的向量,fm+1~f2m为所述待测量电信号经快速离散傅里叶变换后,生成的信号频谱中正频率部分对应的任一谐波或间谐波的频率,f0为所述训练后的第一子函数对应的频率中心,m为所述待测量电信号中谐波和间谐波个数的总和;
所述待测量电信号中谐波的幅值或间谐波的幅值通过以下公式确定:
其中,a’为所述待测量电信号中谐波的幅值和间谐波的幅值组成的向量,am+1~a2m为所述待测量电信号经快速离散傅里叶变换后,生成的信号频谱中正频率部分对应的任一谐波或间谐波的幅值,a为根据所述训练后的第一子函数对应的权值和所述训练后的第二子函数对应的权值计算出的幅值向量,m为所述待测量电信号中谐波和间谐波个数的总和,α为高斯窗参数,λr为所述训练后的第一子函数对应的权值,λi为所述训练后的第二子函数对应的权值,j为虚数单位,||表示取绝对值;
所述待测量电信号中谐波的相位或间谐波的相位通过以下公式确定:
其中,
如此,本申请实施例对采样后的电信号时域加高斯窗处理并做快速离散傅里叶变换后,通过对频谱进行抽选,可以规避高斯窗快速离散傅里叶变换后相邻点相位180°的变化,根据快速离散傅里叶变换后的频谱的波峰数量,构造一系列高斯径向基函数,利用这一系列高斯径向基函数的线性叠加来逼近发生谱间干扰的的频谱,能准确地区分出电信号中产生主瓣干扰的谐波和间谐波成分,测量精度较高。
附图说明
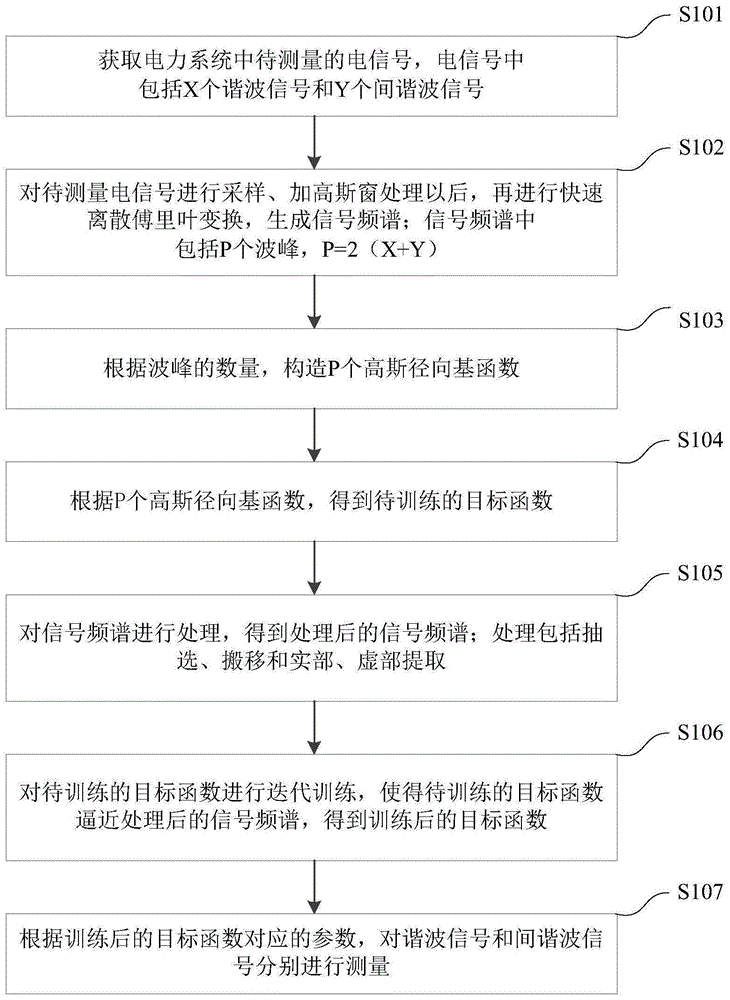
图1为本申请实施例提供的一种电力系统中谐波和间谐波的测量方法所对应的流程示意图;
图2为本申请实施例中获取到的电信号的10个周波的波形示意图;
图3为本申请实施例中信号加高斯窗处理并进行快速离散傅里叶变换后生成的信号频谱示意图;
图4a为本申请实施例中信号经过频谱搬移后的实部频谱示意图;
图4b为本申请实施例中信号经过频谱搬移后的虚部频谱示意图;
图5a为本申请实施例中信号经过抽选后的实部频谱示意图;
图5b为本申请实施例中信号经过抽选后的虚部频谱示意图;
图6为本申请实施例中待训练的目标函数逼近整理后的信号实部频谱的过程中频率中心的变化示意图;
图7为本申请实施例中待训练的目标函数逼近整理后的信号实部频谱的过程中权值的变化示意图;
图8为本申请实施例中待训练的目标函数逼近整理后的信号虚部频谱的过程中权值的变化示意图;
图9为本申请实施例提供的一种电力系统中谐波和间谐波的测量方法所对应的整体性的流程示意图;
图10为本申请实施例提供的一种电力系统中谐波和间谐波的测量装置的结构示意图。
具体实施方式
为使本申请的目的、技术方案和优点更加清楚,下面将结合附图对本申请实施方式作进一步地详细描述。
由于电力系统中广泛应用的各类负载装置很多都是波动的,因此波动负载产生的间谐波污染问题日益加剧。间谐波会给电力系统带来很多危害,严重影响电能质量,因此对间谐波进行准确地检测和分析有着重要的意义。
电力系统的谐波分析通常是采用快速傅里叶变换的方法,同步采样的条件下可以准确的计算谐波分量,但间谐波非工频整数倍,若直接采用快速傅里叶变换算法会产生非整周期截断,进而使得测量含有间谐波的信号时通常会出现频谱泄露,频率相近的谐波和间谐波之间还会产生谱间干扰,严重影响谐波和间谐波的测量精度。
针对上述情况,现有技术一般采用在时域加合适的窗函数来降低频谱泄露,并在此基础上采用插值修正的方法来测量谐波和间谐波。在时域加窗函数的过程中,通过增加窗函数时域的宽度来提高频率分辨率,进而抑制谱间干扰,但由于不确定原理的限制,同时由于实际信号的时变特性,不可能通过无限增加窗函数时域的宽度来增加频率分辨率,因此一般通过增加频域窗函数主瓣的宽度来降低旁瓣的衰减度,但是窗函数主瓣宽度的增加会降低频率分辨率,进而导致频率相近的谐波与间谐波之间的频谱发生重叠干涉,产生主瓣干扰,难以区分电力系统中电信号的谐波和间谐波,进而导致插值修正方法很难对谐波和间谐波进行准确地测量。
基于上述问题,本申请实施例提供一种电力系统中谐波和间谐波的测量方法,如图1所示,为本申请实施例提供的一种电力系统中谐波和间谐波的测量方法所对应的流程示意图。
具体包括如下步骤:
步骤101,获取电力系统中待测量的电信号,电信号包括x个谐波信号和y个间谐波信号。
步骤102,对待测量电信号进行采样、加高斯窗处理以后,再进行快速离散傅里叶变换,生成信号频谱;信号频谱中包括p个波峰,p=2(x+y)。
步骤103,根据波峰的数量,构造p个高斯径向基函数。
步骤104,根据p个高斯径向基函数,得到待训练的目标函数。
步骤105,对信号频谱进行处理,得到处理后的信号频谱;处理包括抽选、搬移和实部、虚部提取。
步骤106,对待训练的目标函数进行迭代训练,使得待训练的目标函数逼近处理后的信号频谱,得到训练后的目标函数。
步骤107,根据训练后的目标函数对应的参数,对谐波信号和间谐波信号分别进行测量。
本申请实施例中,对采样后的电信号时域加高斯窗处理并做快速离散傅里叶变换后,通过对频谱进行抽选,可以规避高斯窗快速离散傅里叶变换后相邻点相位180°的变化,根据快速离散傅里叶变换后的频谱的波峰数量,构造一系列高斯径向基函数,利用这一系列高斯径向基函数的线性叠加来逼近发生谱间干扰的的频谱,能准确地区分出电信号中产生主瓣干扰的谐波和间谐波成分,测量精度较高。
具体来说,步骤101中,交流非正弦信号可以分解为不同频率的正弦分量的线性组合,当正弦波分量的频率是原交流信号的频率的整数倍时,称为谐波;当正弦波分量的频率是原交流信号的频率的非整数倍时,称为间谐波;当正弦波分量的频率与原交流信号的频率相同时,称为基波。为了研究方便,本申请实施例中把基波看做为一次谐波,归于谐波一类中处理。本申请实施例中,获取到的待测量电信号在时域上是连续的。
步骤102中,信号频谱具体可以通过以下方式得到:
对待测量电信号进行采样,将时域连续的信号离散为一个个信号点,采样后得到的多个信号点采用以下公式确定:
公式(1)中,p(n)为采样后得到的信号点,n是信号点,k为整数,m为待测量电信号中所有谐波和间谐波个数的总和,ak为待测量电信号中任一谐波或间谐波的幅值,fk为待测量电信号中任一谐波或间谐波的频率,fs为采样频率,
对采样后得到的多个信号点加宽度为t的高斯窗w(n)后,再进行快速离散傅里叶变换,得到快速离散傅里叶变换后的信号点,高斯窗采用以下公式表示:
t=n×δt公式(3)
公式(2)和公式(3)中,w(n)为高斯窗函数,α为高斯窗参数,n取整数,n取偶数,表示加高斯窗后信号点的数量;z为整数,t为窗函数宽度,δt为采样时间间隔。
快速离散傅里叶变换后的信号点采用以下公式确定:
公式(4)中,pw(n)为快速离散傅里叶变换后的信号点,n是信号点,k为整数,m为待测量电信号中所有谐波和间谐波个数的总和,ak为待测量电信号中任一谐波或间谐波的幅值,n取偶数,表示加高斯窗后信号点的数量;fk为待测量电信号中任一谐波或间谐波的频率,fs为采样频率,
根据这些快速离散傅里叶变换后的信号点,生成信号频谱。
根据快速离散傅里叶变换的理论知识可知,信号经过快速离散傅里叶变换后,还会生成负频率部分,负频率部分与正频率部分是对称的,但是实际计算中负频率部分通常不需要在信号频谱中呈现,本领域技术人员可以根据经验和实际需要来决定是否需要在信号频谱中呈现负频率部分。若待测量电信号中含有x个谐波信号和y个间谐波信号,假设每一个谐波或间谐波都会在信号频谱中形成波峰,则信号频谱中包含的波峰的数量(设为p)等于待测量电信号中所有谐波和间谐波个数的总和的二倍,即p=2(x+y)。
步骤103中,根据信号频谱中波峰的数量,构造p个高斯径向基函数。构造的p个高斯径向基函数采用以下公式确定:
公式(5)中,φi为p个高斯径向基函数中的任意一个,ε为高斯窗的形状参数,α为高斯窗参数,n取偶数,表示加高斯窗后信号点的数量;nf为频率取值的数据集合,t为窗函数宽度,fi为p个高斯径向基函数中的任意一个的频率中心,z为整数,p为构造的高斯径向基函数的个数。
步骤104中,通过对构造的p个高斯径向基函数进行加权求和,得到的待训练的目标函数采用以下公式确定:
公式(6)中,
步骤105中,处理后的信号频谱具体可以通过以下方式得到:
对信号频谱进行抽选、搬移,得到整理后的信号频谱;本申请实施例中,具体采用每隔一个点取一个点的方式对信号频谱进行抽选,该整理后的信号频谱对应的信号点采用以下公式表示:
公式(7)中,pws(n)为整理后的信号频谱对应的信号点,pw(k)为快速离散傅里叶变换后的第k个信号点,k的取值为
对整理后的信号频谱进行实部提取,得到整理后的信号实部频谱,其对应的函数采用以下公式确定:
r_pws(n)=real[pws(n)]公式(8)
公式(8)中,r_pws(n)为整理后的信号实部频谱对应的函数,real表示取实部的运算,pws(n)为整理后的信号频谱对应的信号点
对整理后的信号频谱进行虚部提取,得到整理后的信号虚部频谱,其对应的函数采用以下公式确定:
i_pws(n)=imag[pws(n)]公式(9)
公式(9)中,i_pws(n)为整理后的信号虚部频谱对应的函数,imag表示取虚部的运算,pws(n)为整理后的信号频谱对应的信号点
将整理后的信号实部频谱和整理后的信号虚部频谱共同作为处理后的信号频谱。
采用上述示例中每隔一个点取一个点的抽选方法对信号频谱进行处理,可以规避高斯窗快速离散傅里叶变换后相邻点相位180°的变化,便于后续数据分析。
步骤106中,对待训练的目标函数进行训练的方式有多种,一个示例中,可以采用梯度下降法对待训练的目标函数进行迭代训练,使得待训练的目标函数逼近处理后的信号频谱,得到训练后的目标函数。具体可以通过以下方式实现:
设置第一损失函数:
公式(10)中,e1为第一损失函数,
设置训练调节公式:
λj(k)=λj(k-1)+δλj(k)+β[λj(k-1)-λj(k-2)]公式(12)
fj(k)=fj(k-1)+δfj(k)+β[fj(k-1)-fj(k-2)]公式(14)
公式(11)和公式(12)中,λj(k)为训练过程中第k个权值向量中的第j个权值,δλj(k)为λj(k)的调节值,e1(k)为第k个第一损失函数,k是训练次数,φj(k)为训练过程中第k个高斯径向基函数向量中的第j个高斯径向基函数,
公式(13)和公式(14)中,fj(k)为训练过程中第k个频率中心向量中的第j个频率中心,δfj(k)为fj(k)的调节值,e1(k)为第k个第一损失函数,ε为高斯窗的形状参数,λj(k)为训练过程中第k个权值向量中的第j个权值,k是训练次数,φj(k)为训练过程中第k个高斯径向基函数向量中的第j个高斯径向基函数,
为梯度下降法设置运算初始值λ(1)和f(1):信号经过快速离散傅里叶变换后生成的信号频谱中,每个波峰都有对应的频率,将这p个频率组成的向量作为梯度下降法的初始频率向量f(1),fj(1)为初始频率向量中的第j个频率(j=1,…,p);将p个0组成的向量作为梯度下降法的初始权值向量λ(1),λj(1)为初始权值向量中的第j个权值(j=1,…,p)。
然后k从2开始,利用公式(11)、公式(12)、公式(13)和公式(14)对λj(k)和fj(k)进行训练调节,直到计算出的第一损失函数e1的值小于预设阈值δ,循环计算停止,将循环计算停止时的频率中心向量f(k)作为训练后的目标函数对应的频率中心,将循环计算停止时的权值向量λ(k)作为训练后的目标函数对应的权值;将f(k)和λ(k)代入待训练的目标函数
将循环计算停止时的频率中心向量f(k),即训练后的目标函数对应的频率中心,代入待训练的目标函数
设置第二损失函数:
公式(15)中,e2为第二损失函数,
重新设置训练调节公式:
λ′j(k)=λ′j(k-1)+δλ′j(k)+β[λ′j(k-1)-λ′j(k-2)]公式(17)
公式(16)和公式(17)中,λ′j(k)为训练过程中第k个权值向量中的第j个权值,δλ′j(k)为λ′j(k)的调节值,e2(k)为第k个第二损失函数,k是训练次数,φ′j(k)为训练过程中第k个高斯径向基函数向量中的第j个高斯径向基函数,也就是待训练的中间函数
为梯度下降法设置运算初始值λ′j(1):将p个0组成的向量作为梯度下降法的初始权值向量λ’(1),λ′j(1)为初始权值向量中的第j个权值(j=1,…,p)。
然后k从2开始,利用公式(16)和公式(17)对λ′j(k)进行训练调节,直到计算出的第二损失函数e2的值小于预设阈值δ,循环计算停止,将循环计算停止时的权值向量λ’(k)作为训练后的中间函数对应的权值;将λ’(k)代入待训练的中间函数
将经过上述训练过程得到的训练后的第一子函数和训练后的第二子函数,共同作为训练后的目标函数。
采用上述训练方法,通过构造高斯径向基函数的线性叠加分别逼近频谱的实部和虚部,克服标准高斯函数及其傅里叶变换只为实函数的问题,通过梯度下降法迭代求取高斯径向基函数的中心和权值,避免了现有技术中径向基函数插值矩阵的求逆问题。
在其它可能的示例中,本领域技术人员可以根据经验和实际情况来确定待训练的目标函数的训练方法,比如,可以采用最小二乘法来训练,具体不作限定。
步骤107中,步骤106中训练后的目标函数对应的参数包括:训练后的第一子函数对应的频率中心f0、训练后的第一子函数对应的权值λr和训练后的第二子函数对应的权值λi。
待测量电信号中谐波的频率或间谐波的频率通过以下方式确定:
公式(18)中,f′0为待测量电信号中谐波的频率和间谐波的频率组成的向量,fm+1~f2m为待测量电信号经快速离散傅里叶变换后,生成的信号频谱中正频率部分对应的任一谐波或间谐波的频率;f1~fm与fm+1~f2m互为相反数,表示待测量电信号经快速离散傅里叶变换后,生成的信号频谱中负频率部分对应的任一谐波或间谐波的频率,所述负频率部分是傅里叶变换的运算过程中产生的结果,在迭代训练过程中用于对结果的验证;其中,f1~fm与fm+1~f2m互为相反数,可以是f1=-f2m、f2=-f(2m-1)、……,或者,也可以是f1=-f(m+1)、f2=-f(m+2)、……,两个数据集合中每一个数据如何对应具体不作限定;f0为训练后的第一子函数对应的频率中心,m为待测量电信号中谐波和间谐波个数的总和。
待测量电信号中谐波的幅值或间谐波的幅值通过以下公式确定:
公式(19)中,a’为待测量电信号中谐波的幅值和间谐波的幅值组成的向量,am+1~a2m为待测量电信号经快速离散傅里叶变换后,生成的信号频谱中正频率部分对应的任一谐波或间谐波的幅值;a1~am与am+1~a2m的数值相同,表示待测量电信号经快速离散傅里叶变换后,生成的信号频谱中负频率部分对应的任一谐波或间谐波的幅值,所述负频率部分是傅里叶变换的运算过程中产生的结果,在迭代训练过程中用于对结果的验证;其中,a1~am与am+1~a2m数值相同,可以是a1=a2m、a2=a(2m-1)、……,或者,也可以是a1=a(m+1)、a2=a(m+2)、……,两个数据集合中每一个数据如何对应具体不作限定;a为根据训练后的第一子函数对应的权值和训练后的第二子函数对应的权值计算出的幅值向量,m为待测量电信号中谐波和间谐波个数的总和,α为高斯窗参数,λr为训练后的第一子函数对应的权值,λi为训练后的第二子函数对应的权值,j为虚数单位,||表示取绝对值
待测量电信号中谐波的相位或间谐波的相位通过以下公式确定:
公式(20)中,
为了更加清楚地说明步骤101至步骤107所描述的方法,下面通过具体示例来说明。
假设电力系统中的电信号采用的是ieee间谐波工作组提供的仿真信号,包含50hz基波、250hz的5次谐波、104hz、117hz、134hz和147hz四个间谐波,参数如表1所示。
表1:电信号中包含的谐波参数和间谐波参数的一种示例
按照1000hz的频率对电信号进行采样,采用高斯窗参数α=4、宽度为0.2s的高斯窗,对采样的信号点进行处理,共截取得到200个点,共10个周波。图2示例性示出了本申请实施例中获取到的电信号的10个周波的波形示意图。
对这些加窗处理后的信号点做快速离散傅里叶变换,生成较为直观的信号频谱。图3示例性示出了本申请实施例中信号加高斯窗处理并进行快速离散傅里叶变换后生成的信号频谱示意图。如图3所示,因基波归于谐波中处理,因此图中有两个谐波、四个间谐波,共形成了六个波峰,其中四个间谐波之间发生了谱间干扰现象;由于信号经快速离散傅里叶变换后还会生成与正频率对称的负频率部分,因此信号频谱中实际上应包括十二个波峰。基于此,按照公式(5)构造十二个高斯径向基函数,其中高斯窗的形状参数ε=55.536,nf=[-500,-490,-480,…,-10,0,10,…,480,490]t。根据对这十二个高斯径向基函数加权求和,依据公式(6)构造出待训练的目标函数
根据公式(7)的方法对信号频谱进行抽选和搬移,然后按照公式(8)的方法取整理后的信号点的实部,按照公式(9)的方法取整理后的信号点的虚部。图4a示例性示出了本申请实施例中信号经过频谱搬移后的实部频谱示意图,图4b示例性示出了本申请实施例中信号经过频谱搬移后的虚部频谱示意图,图5a示例性示出了本申请实施例中信号经过抽选后的实部频谱示意图,图5b示例性示出了本申请实施例中信号经过抽选后的虚部频谱示意图。
为梯度下降法设置运算初始值:将十二个波峰对应的频率作为初始频率f(1)=[f1,f2,…,f12]t=[-250,-147.27,-134.09,-117.27,-103.64,-50,50,103.64,117.27,134.09,147.27,250]t,将λ(1)中的12个值均取0,作为初始权值。学习速率η=0.03,动量因子β=0.05,预设阈值为0.0001,根据公式(10)~公式(17),利用梯度下降法迭代训练了30000次,使得待训练的目标函数分别逼近整理后的信号频谱的实部和虚部,计算得出训练后的第一子函数对应的频率中心f0、训练后的第一子函数对应的权值λr和训练后的第二子函数对应的权值λi。图6示例性示出了本申请实施例中待训练的目标函数逼近整理后的信号实部频谱的过程中频率中心的变化示意图,图7示例性示出了本申请实施例中待训练的目标函数逼近整理后的信号实部频谱的过程中权值的变化示意图,图8示例性示出了本申请实施例中待训练的目标函数逼近整理后的信号虚部频谱的过程中权值的变化示意图。
根据公式(18)、公式(19)和公式(20),得到电信号中包含的谐波或间谐波的频率、幅值和相位。测量得到的具体参数汇总如表2所示。表2中除了间谐波的相位有很小的误差,其它参数的精准度都很高。
表2:电信号中包含的谐波的测量结果和间谐波的测量结果的一种示例
为了更加清楚地描述上述内容,如图9所示,为本申请实施例提供的一种电力系统中谐波和间谐波的测量方法所对应的整体性的流程示意图。具体包括如下步骤:
步骤901,获取电力系统中待测量电信号,电信号包括x个谐波信号和y个间谐波信号。
步骤902,对待测量电信号进行采样、加高斯窗处理以后,再进行快速离散傅里叶变换,生成信号频谱;信号频谱包括p个波峰,p=2(x+y)。
步骤903,构造p个高斯径向基函数。
步骤904,对p个高斯径向基函数加权求和得到待训练的目标函数。
步骤905,对信号频谱进行处理,得到整理后的信号实部频谱和整理后的信号虚部频谱;处理包括抽选、搬移和实部、虚部提取。
步骤906,根据待训练的目标函数和整理后的信号实部频谱对应的函数,确定第一损失函数e1。
步骤907,设置运算初始值f(1)和λ(1)。
步骤908,设置梯度下降法训练调节公式,循环更新f(k)和λ(k),计算第一损失函数e1的值。
步骤909,判断第一损失函数e1的值是否小于预设阈值δ,如果e1的值大于或等于预设阈值δ,则执行步骤910;否则,执行步骤911。
步骤910,k取k+1,重新执行步骤908和步骤909。
步骤911,将循环计算停止时的频率中心向量作为训练后的第一子函数对应的频率中心f0,将循环计算停止时的权值向量作为训练后的第一子函数对应的权值λr。
步骤912,将f0代入待训练的目标函数,得到待训练的中间函数;根据待训练的中间函数和整理后的信号虚部频谱对应的函数,确定第二损失函数e2。
步骤913,设置运算初始值λ’(1)。
步骤914,重新设置梯度下降法训练调节公式,循环更新λ(k),计算第二损失函数e2的值。
步骤915,判断第二损失函数e2的值是否小于预设阈值δ,如果e1的值大于或等于预设阈值δ,则执行步骤916;否则,执行步骤917。
步骤916,k取k+1,重新执行步骤914和步骤915。
步骤917,将循环计算停止时的权值向量作为训练后的第二子函数对应的权值λr。
步骤918,计算电信号中谐波的频率或间谐波的频率、谐波的幅值或间谐波的幅值、谐波的相位或间谐波的相位。
如此,本申请实施例中通过对采样后的电信号时域加高斯窗处理,并做快速离散傅里叶变换计算频谱,根据频谱的波峰数量构造高斯径向基函数,通过对频谱数据抽选和搬移来进行整理,可以规避高斯窗快速离散傅里叶变换后相邻点相位180°的变化;再应用梯度下降法使构造的高斯径向基函数的线性叠加逼近整理后的频谱的实部和虚部,从而测量谐波和间谐波的参数,可以克服标准高斯函数及其傅里叶变换只为实函数的问题,通过梯度下降法迭代训练,可以避免径向基函数插值矩阵的求逆问题。
下述为本申请装置实施例,可以用于执行本申请方法实施例。对于本申请装置实施例中未披露的细节,请参照本申请方法实施例。
图10示例性示出了本申请实施例提供的一种电力系统中谐波和间谐波的测量装置的结构示意图。如图10所示,该装置具有实现上述电力系统中谐波和间谐波的测量方法的功能,所述功能可以由硬件实现,也可以由硬件执行相应的软件实现。该装置可以包括:获取单元1001,处理单元1002和测量单元1003。
获取单元1001,用于获取电力系统中待测量电信号,所述电信号包括x个谐波信号和y个间谐波信号。
处理单元1002,用于对待测量电信号进行采样、加高斯窗处理以后,再进行快速离散傅里叶变换,生成信号频谱;所述信号频谱中包括p个波峰,p=2(x+y);以及,根据波峰的数量,构造p个高斯径向基函数;以及,根据p个高斯径向基函数,得到待训练的目标函数;以及,对信号频谱进行图像处理,得到处理后的信号频谱;所述处理包括抽选、搬移和实部、虚部提取;以及,对待训练的目标函数进行迭代训练,使得待训练的目标函数逼近所述处理后的信号频谱,得到训练后的目标函数。
测量单元1003,用于根据训练后的目标函数对应的参数,对谐波信号和间谐波信号分别进行测量。
在一种可实现方式中,所述处理单元1002具体用于:
对待测量电信号进行采样、加高斯窗处理以后,再进行快速离散傅里叶变换,得到快速离散傅里叶变换后的信号点;以及,根据快速离散傅里叶变换后的信号点,生成信号频谱。
在一种可实现方式中,快速离散傅里叶变换后的信号点通过以下公式确定:
其中,pw(n)为快速离散傅里叶变换后的信号点,n是信号点,k为整数,m为待测量电信号中谐波和间谐波个数的总和,ak为待测量电信号中任一谐波或间谐波的幅值,n取偶数,表示加高斯窗后信号点的数量;fk为待测量电信号中任一谐波或间谐波的频率,fs为采样频率,
在一种可实现方式中,所述处理单元1002具体用于:
对p个高斯径向基函数进行加权求和,得到待训练的目标函数。
在一种可实现方式中,待训练的目标函数通过以下公式表示:
其中,φi为p个高斯径向基函数中的任意一个,ε为高斯窗的形状参数,α为高斯窗参数,n取偶数,表示加高斯窗后信号点的数量;nf为频率取值的数据集合,t为窗函数宽度,fi为p个高斯径向基函数中的任意一个的频率中心,z为整数,
在一种可实现方式中,所述处理单元1002具体用于:
对信号频谱进行抽选、搬移,得到整理后的信号频谱;以及,对整理后的信号频谱进行实部提取,得到整理后的信号实部频谱;以及,对整理后的信号频谱进行虚部提取,得到整理后的信号虚部频谱;以及,将整理后的信号实部频谱和整理后的信号虚部频谱共同作为处理后的信号频谱。
在一种可实现方式中,整理后的信号实部频谱对应的函数和整理后的信号虚部频谱对应的函数通过以下公式确定:
r_pws(n)=real[pws(n)]
i_pws(n)=imag[pws(n)]
其中,pws(n)为整理后的信号频谱对应的信号点,r_pws(n)为整理后的信号实部频谱对应的函数,i_pws(n)为整理后的信号虚部频谱对应的函数,real表示取实部的运算,imag表示取虚部的运算。
在一种可实现方式中,所述处理单元1002具体用于:
根据待训练的目标函数和整理后的信号实部频谱对应的函数,确定第一损失函数;以及,利用梯度下降法对待训练的目标函数对应的频率中心和待训练的目标函数对应的权值进行训练,使得第一损失函数达到最小值,确定训练后的目标函数对应的频率中心和训练后的目标函数对应的权值;以及,将训练后的目标函数对应的频率中心和训练后的目标函数对应的权值代入待训练的目标函数,确定训练后的第一子函数;以及,将训练后的目标函数对应的频率中心代入待训练的目标函数,得到待训练的中间函数;以及,根据待训练的中间函数和整理后的信号虚部频谱对应的函数,确定第二损失函数;以及,利用梯度下降法对待训练的中间函数对应的权值进行训练,使得第二损失函数达到最小值,确定训练后的中间函数对应的权值;以及,将训练后的中间函数对应的权值代入待训练的中间函数,确定训练后的第二子函数;以及,将训练后的第一子函数和训练后的第二子函数共同作为训练后的目标函数。
在一种可实现方式中,训练后的目标函数对应的参数包括训练后的第一子函数对应的频率中心、训练后的第一子函数对应的权值、训练后的第二子函数对应的权值。
待测量电信号中谐波的频率或间谐波的频率通过以下方式确定:
其中,f′0为待测量电信号中谐波的频率和间谐波的频率组成的向量,fm+1~f2m为待测量电信号经快速离散傅里叶变换后,生成的信号频谱中正频率部分对应的任一谐波或间谐波的频率,f0为训练后的第一子函数对应的频率中心,m为待测量电信号中谐波和间谐波个数的总和。
待测量电信号中谐波的幅值或间谐波的幅值通过以下公式确定:
其中,a’为待测量电信号中谐波的幅值和间谐波的幅值组成的向量,am+1~a2m为待测量电信号经快速离散傅里叶变换后,生成的信号频谱中正频率部分对应的任一谐波或间谐波的幅值,a为根据训练后的第一子函数对应的权值和训练后的第二子函数对应的权值计算出的幅值向量,m为待测量电信号中谐波和间谐波个数的总和,α为高斯窗参数,λr为训练后的第一子函数对应的权值,λi为训练后的第二子函数对应的权值,j为虚数单位,||表示取绝对值。
待测量电信号中谐波的相位或间谐波的相位通过以下公式确定:
其中,
如此,本申请实施例对采样后的电信号时域加高斯窗处理并做快速离散傅里叶变换后,通过对频谱进行抽选,可以规避高斯窗快速离散傅里叶变换后相邻点相位180°的变化,根据快速离散傅里叶变换后的频谱的波峰数量,构造一系列高斯径向基函数,利用这一系列高斯径向基函数的线性叠加来逼近发生谱间干扰的的频谱,能准确地区分出电信号中产生主瓣干扰的谐波和间谐波成分,测量精度较高。
在示例性实施例中,还提供了一种计算机可读存储介质,所述存储介质中存储有计算机程序或智能合约,所述计算机程序或智能合约被节点加载并执行以实现上述实施例提供的事务处理方法。可选地,上述计算机可读存储介质可以是只读存储记忆体(read-onlymemory,rom)、随机存储记忆体(randomaccessmemory,ram)、cd-rom、磁带、软盘和光数据存储设备等。
本领域的技术人员可以清楚地了解到本申请实施例中的技术可借助软件加必需的通用硬件平台的方式来实现。基于这样的理解,本申请实施例中的技术方案本质上或者说对现有技术做出贡献的部分可以以软件产品的形式体现出来,该计算机软件产品可以存储在存储介质中,如rom/ram、磁碟、光盘等,包括若干指令用以使得一台计算机设备(可以是个人计算机,服务器,或者网络设备等)执行本申请各个实施例或者实施例的某些部分所述的方法。
本领域技术人员在考虑说明书及实践这里公开的发明后,将容易想到本公开的其它实施方案。本申请旨在涵盖本公开的任何变型、用途或者适应性变化,这些变型、用途或者适应性变化遵循本公开的一般性原理并包括本公开未公开的本技术领域中的公知常识或惯用技术手段。说明书和实施例仅被视为示例性的,本公开的真正范围和精神由下面的权利要求指出。
应当理解的是,本公开并不局限于上面已经描述并在附图中示出的精确结构,并且可以在不脱离其范围进行各种修改和改变。本公开的范围仅由所附的权利要求来限制。
- 还没有人留言评论。精彩留言会获得点赞!