基于声学信号的路面构造深度检测方法及装置与流程

本发明涉及路面信息检测的技术领域，具体涉及一种基于声学信号的路面构造深度检测方法及装置。

背景技术：

在现代路面养护管理工作中，路面构造深度也用于评价路面磨耗和路面抗滑性能；对路面构造深度的检测和评价不仅是各个国路面养护规范的重要组成部分，还影响着公众驾驶出行的行车安全性和稳定性。以目前最常用的公路路面沥青路面为例，沥青结合料提高了铺路用粒料抵抗行车和自然因素对路面损害的能力，使路面平整少尘、不透水、经久耐用，所以沥青路面是道路建设中一种被最广泛采用的高级路面。路面构造深度是沥青路面粗糙度的重要指标，反映沥青路面的宏观构造。如何用一种低成本、易操作的方式，对路面构造深度进行快速、实时的检测和评价成为了当前道路路面检测和维修养护的重点和难点。

现有技术中提供了一种通过采集轮胎-路面噪声信息数据来推导预测沥青路面构造深度的技术方案。该技术方案主要通过采集同一轮胎在不同速度、不同路面类型状况下的各种噪声数据信息，通过matlab软件编程将轮胎与路面噪声试验数据进行傅里叶变换。使用excel软件将数据标准化并运用主成分分析法，选取出代表路面特性的声压级数据作为第一主成分分量；再将测试路面的声压级数据与已知路面的声压级数据之间的向量夹角作比较，得出对沥青路面构造深度的预测结果。上述技术方案是通过既有的沥青路面构造深度数据，来预测待检测的沥青路面构造深度，两者之间是一种简单的数据映射关系，所以采用上述技术方案在进行数据处理时处理效率低，得到的沥青路面构造深度预测数据精确度不够高，特别是在车速达到80km/h后，预测计算精度不到80％。

技术实现要素：

针对现有技术中的缺陷，本发明提供一种基于声学信号的路面构造深度检测方法及装置，以解决现有技术中存在的使用声学信号预测路面构造深度时，仅仅是采用简单的数据映射对比，得到的路面构造深度数据不够精确的技术问题。

本发明采用的技术方案如下：

第一方面，提供了一种基于声学信号的路面构造深度检测方法；

第一种可实现方式，包括以下步骤：

通过安装于车辆轮胎旁侧的声音传感器采集声学信号，声学信号为轮胎/路面噪声；

使用主成分分析法提取出声学信号的第一主成分分量；第一主成分分量为声压级；

将第一主成分分量输入非线性混合高斯模型，获取非线性混合高斯模型的输出作为路面构造深度。

结合第一种可实现方式，在第二种可实现方式中，非线性混合高斯模型为：

y＝m(μ1:k,1:d,x1:n,1:d)α1:1+d+k,1:c+nt

其中，y为路面构造深度，μ为径向基函数的中心参数，k为基函数个数，x为第一主成分分量，n为第一主成分分量的个数，d为输入变量x维度，a为径向基函数的幅度值，c为输出变量y维度；nt为零均值的高斯噪声；参数a、d、k、c、μ与模型空间参数集θ相关联；

模型空间参数集信息和模型基函数个数信息是利用可逆马尔科夫链蒙特卡洛算法确定的。

结合第二种可实现方式，在第三种可实现方式中，利用可逆马尔科夫链蒙特卡洛算法确定模型空间参数集信息和模型基函数个数信息，包括以下步骤：

对模型空间参数集信息和模型基函数个数信息进行初始化设置，采用极大似然估计法设置目标初始值；

进行迭代采样，根据计算接受概率对马尔科夫链进行更新；

基于新的马尔科夫链更新分层模型参数；

进行全贝叶斯模型收敛性判断，模型收敛退出迭代。

结合第一种可实现方式，在第四种可实现方式中，使用主成分分析法对声学信号提取第一主成分分量，包括以下步骤：

对采集到的轮胎/路面噪声信号进行时域a计权滤波，得到时域信号；

对时域信号进行滑动加窗傅里叶变换，通过低通滤波器保留低频信号；

对低频段信号进行主成分分析，取出代表整个滑动窗周期内的第一主成分分量。

结合第一种可实现方式，在第五种可实现方式中，将第一主成分分量输入非线性混合高斯模型之前还包括：对第一主成分分量进行速度的干扰抑制。

结合第五种可实现方式，在第六种可实现方式中，对第一主成分分量进行速度的干扰抑制，包括：

利用如下公式，将从声学信号中提取到的第一主成分分量转换为标准化速度对应的第一主成分分量

其中，ln为标准化速度下对应的第一主成分分量，lc为从声学信号中提取到的第一主成分分量，vn为标准化速度，vc为采集声学信号时的实际速度。

第二方面，提供了一种基于声学信号的路面构造深度检测装置，

在第七种可实现方式中，检测装置包括：声音采集单元、数据传输单元、计算单元和控制单元；

声音采集单元用于采集声学信号，数据传输单元用于将声学信号传输给计算单元，计算单元用于根据声学信号计算路面构造深度，控制单元用于控制音频采集单元、数据传输单元和计算单元工作。

结合第七种可实现方式，在第八种可实现方式中，声音采集单元包括多个声音传感器，多个声音传感器分别安装于车辆轮胎旁侧。

结合第七种可实现方式，在第九种可实现方式中，数据传输单元采用无线传输方式进行数据传输。

结合第七种可实现方式，在第十种可实现方式中，计算单元包括处理器和存储器；存储器用于存储执行第一到第六种可实现方式中任一项方法的程序；处理器被配置为执行存储器中存储的程序。

由上述技术方案可知，本发明的有益技术效果如下：

1.使用声压级和高斯函数构建声学信号的非线性混合高斯模型，通过可逆跳转马尔科夫链蒙特卡罗算法进行贝叶斯计算,完成模型的构建；使用模型计算路面构造深度。通过这种方法，可以更为精确的检测计算出路面的构造深度。

2.在计算过程中，通过对声压级进行速度的干扰抑制处理，消除了行车速度对轮胎/路面噪声信号的干扰，使计算结果更加准确。

附图说明

为了更清楚地说明本发明具体实施方式或现有技术中的技术方案，下面将对具体实施方式或现有技术描述中所需要使用的附图作简单地介绍。在所有附图中，类似的元件或部分一般由类似的附图标记标识。附图中，各元件或部分并不一定按照实际的比例绘制。

图1为本发明的方法流程图。

图2为本发明的声音传感器安装位置示意图。

图3为本发明的非线性混合高斯模型的完整层次图。

图4为本发明的装置架构图。

附图标记：

1-轮胎，2-轮毂，3-金属支架，4-声音传感器。

具体实施方式

下面将结合附图对本发明技术方案的实施例进行详细的描述。以下实施例仅用于更加清楚地说明本发明的技术方案，因此只作为示例，而不能以此来限制本发明的保护范围。

需要注意的是，除非另有说明，本申请使用的技术术语或者科学术语应当为本发明所属领域技术人员所理解的通常意义。

实施例1

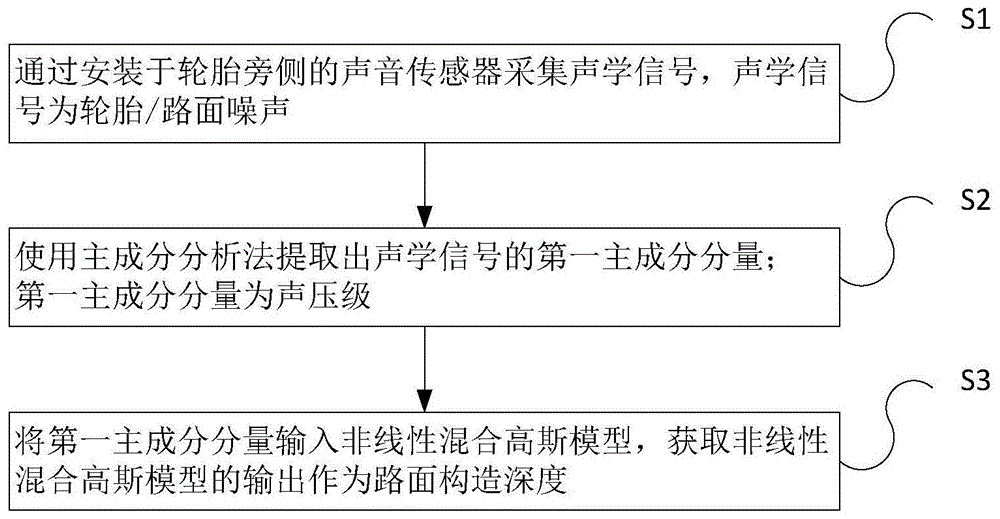
如图1所示，本发明提供一种基于声学信号的路面构造深度检测方法，包括以下步骤：

通过安装于车辆轮胎旁侧的声音传感器采集声学信号，声学信号为轮胎/路面噪声；

使用主成分分析法提取出声学信号的第一主成分分量；第一主成分分量为声压级；

将第一主成分分量输入非线性混合高斯模型，获取非线性混合高斯模型的输出作为路面构造深度。

以下对实施例1工作原理进行详细说明：

1.将声音传感器安装在车辆轮胎旁侧，对轮胎/路面噪声信息数据进行采集

在本实施例中，如图2所示，首先将声音传感器的固定装置3安装在车辆轮胎的轮毂2上，固定装置3为一金属架，在本实施例中安装方式可选用螺栓连接。为获得较好的轮胎/路面噪声信息数据采集效果，将声音传感器4的安装位置选在距离轮胎中心点水平距离40cm、距离地面10cm的位置处。声音传感器的数量为2个，其中一个声音传感器安装在左后轮，另一个声音传感器安装在右后轮。

在本实施例中，声音传感器选用麦克风，型号为gras-46ae。麦克风与工控机电连接，当汽车启动后，工控机会控制麦克风开始工作，采集噪声信息，并将采集结果传输到工控机中存储、记录。在本实施例中，轮胎/路面噪声信息数据的采样频率为50khz。

2.使用主成分分析法对声学信号进行处理，提取出第一主成分分量

采用主成分分析法进行预处理，并提取第一主成分分量的目的在于：第一主成分分量能够表征出原始声学信号的绝大部分特性，同时可滤除掉引擎，鸣笛等外界干扰信号。

对采集到的轮胎/路面噪声信号进行时域a计权滤波得到时域信号；再对时域信号进行滑动加窗傅里叶变换，并通过低通滤波器保留40～700hz频段的低频信号；然后将得到的低频段信号进行主成分分析，取出代表整个滑动窗周期内的第一主成分分量，第一主成分分量信号为声压级，该段数据则能够有效表征该时间段内的路面特性。在本实施例中以xt表示经过预处理后的第t个时刻路面声压级，t的取值范围为自然数1到n。

3.使用第一主成分分量和高斯基函数构建声学信号混合高斯模型

通过步骤2得到的第一主成分分量为声压级，将声压级作为一维单输入变量，结合公式(1)、公式(2)和公式(3)，构建非线性混合高斯模型。非线性高斯模型，就是将非线性变量引入混合高斯模型的一种模型，在本实施例中，非线性变量就是声压级。构建模型的具体过程如下：

公式(1)为构建的模型，该模型为非线性混合高斯模型，用于计算路面构造深度；其中，k为基函数的个数，m0为k＝0时的函数关系式，mk为k≥1时的函数关系式，yt为路面构造深度；b和β为混合模型的线性回归参数，xt为经过预处理后的第t个时刻路面声压级，nt为零均值的高斯噪声，aj为为径向基函数的幅度值，μj为第j个径向基函数的中心参数。

公式(2)为输入声学信号所服从的混合高斯分布函数；其中，xt为经过预处理后的第t个时刻路面的声压级，ωj为高斯混合模型分量j的权值，为高斯混合模型中第j个混合分量的概率密度函数。

公式(3)为混合高斯模型中的第j个基函数所服从的高斯分布；其中，为高斯混合模型中第j个混合分量的概率密度函数，x为经过预处理的路面的声压级，μj为第j个径向基函数的中心参数，为第j个径向基函数的方差。

结合公式(1)、(2)和(3)，

把公式(3)带入公式(2)，可得出

然后将公式(4)带入公式(1)，并将其结果变换成为矩阵形式，即可得出声学信号的非线性混合高斯模型，如下式公式(5)：

y＝m(μ1:k,1:d,x1:n,1:d)α1:1+d+k,1:c+nt(5)

在公式(4)中，m和a即为变换后的矩阵，y为路面构造深度，μ为径向基函数的中心参数，k为基函数个数，x为路面声压级，n为声压级的个数，d为输入变量x维度，a为径向基函数的幅度值，c为输出变量y维度；nt为零均值的高斯噪声。由于在模型构建时，路面的构造深度y是已经通过试验测量后得到的真实值,路面声学信号声压级x通过声音传感器采集到，所以在公式(5)中，只有基函数个数k，以及模型空间参数集为非线性混合高斯模型的未知量；模型构建完成并计算得到了k和θ后，便可以使用该模型进行路面构造深度的计算。

对于μ为k个基函数的高斯分布均值，可采用随机漫步方法在输入变量x的范围内确定μ的取值。基函数个数k的先验选为服从均值为λ的泊松分布，满足如下公式(6)：

λ的先验选为服从形状参数ε1和尺度参数ε2的gamma分布，满足如下公式(7)：

λ～ga(ε1,ε2)(7)

子参数空间α的先验选为服从均值为0，方差为δ²与σ²乘积的高斯分布，满足如下公式(8)：

α～n(0,δ²σ²)(8)

δ²的先验选择为服从形状参数a和尺度参数b的逆gamma分布，满足如下公式(9)：

δ²～ig(a,b)(9)

σ²的先验选择为服从形状参数υ0和尺度参数γ0的逆gamma分布，满足如下公式(10)：

σ²～ig(υ0,γ0)(10)

根据公式(6)、公式(7)、公式(8)、公式(9)、公式(10)，可以推导出非线性混合高斯模型的完整层次图，如图3所示，图中方框代表已确定或通过测量已得到的值，圆圈代表未知值。该模型中，x表示路面声压级，y表示对应路面构造深度值。

4.使用可逆跳转马尔科夫链蒙特卡罗算法进行贝叶斯计算,得出基函数个数k和模型空间参数θ

使用可逆跳转蒙特卡罗采样算法进行贝叶斯计算，可以得到基函数的个数信息p(k|x,y)，以及模型空间参数信息p(θ|x,y)。可逆跳转蒙特卡罗采样算法在马尔科夫链上的转移包括如下5个状态：增加、删除、分裂、合并以及更新；其中增加状态是指增加一个新的基函数；删除状态是指从已有的基函数中随机删除一个基函数；分裂状态是指随机选中一个基函数，将其分裂成两个新的基函数；合并状态是指随机选中一个基函数，并将与之最邻近的一个基函数进行合并，形成一个新的基函数；更新状态是指更新基函数。上述5种状态构成一条马尔科夫链，该链的转移核由增加、删除、分裂、合并以及更新5种状态的联合条件概率密度函数构成。在每一次迭代运算中设置转移到增加状态的概率为bk，转移到删除状态的概率为dk,转移到分裂状态的概率为sk,转移到合并状态的概率为mk,转移到更新状态的概率为uk。同时各个转移状态的概率满足下式公式(11)：

在公式(11)中，p(k)为基函数个数为k的模型的先验概率，p为每次迭代模型阶数,基函数个数k发生变化的概率,0≤k≤kmax。

具体的，首先对基函数个数k和模型空间参数θ进行初始化设置，采用极大似然估计法设置目标初始值；然后进行迭代采样，根据计算接受概率，对高斯基函数马尔科夫链进行调整，包括增加、删除、分裂、合并以及更新高斯基函数马尔科夫链；再基于调整后新的马尔科夫链更新分层模型参数(σ²，α)及(λ，δ²)；最后进行全贝叶斯模型收敛性判断，模型收敛则退出迭代。通过步骤4中的算法，可得到模型中基函数的个数信息p(k|x,y)和模型空间参数信息p(θ|x,y)，这样就完成了非线性混合高斯模型的构建。

5.计算路面构造深度

通过步骤4中的算法，可得到模型空间参数信息p(θ|x,y)和模型基函数的个数信息p(k|x,y)。因此路面构造深度的计算公式为：

ymtd＝p(y|θ,k)·xt(12)

在公式(12)中，ymtd为待测的路面构造深度，xt为经过预处理的第t个时刻路面的声压级。

从下表中可以看出，使用实施例1中的算法，相较于现有技术，可以更为精确的检测出计算路面构造深度。表中的构造深度实测值是通过铺砂法测得的。

目前，混合高斯模型被较多的使用在图像识别领域，而在本发明中，通过实施例1中的技术方案，在构建非线性混合高斯模型时，通过可逆跳转马尔科夫链蒙特卡罗算法，能够在不同维的参数空间中跳转,因此可以进行模型阶数k和模型空间参数θ的联合估计，从而使得所构建的非线性混合高斯模型的输出可以无限逼近路面构造深度的真值。通过这种方法，可以更为精确的检测计算出路面的构造深度。

实施例2

在相同的路面上由于行车速度的不同，会引起麦克风采集到的声压级的差异，进而会对ymtd的计算结果形成影响。为解决上述技术问题，在实施例1的基础上进一步优化，采用以下技术方案：

对声压级进行速度的干扰抑制。实现声压级的标准化处理。

以下对实施例2工作原理进行详细说明：

车辆行驶速度是影响轮胎/路面噪声最重要的因素。在同一段路面上采用相同声学信号采集车以50khz的频率进行重复声学信号采集，随着行车速度的增加，对应声压级也相应增加。由于车辆行驶速度在实际行车过程中不能完全保持一成不变，所以只能对采集到的声压级进行速度的干扰抑制，以尽可能地减小速度对声压级的干扰。

对声压级进行速度干扰抑制的计算方法，见下式公式(13)

在公式(13)中，ln为标准化速度下的轮胎/路面噪声声压级，lc为实际速度下的轮胎/路面噪声声压级，vn为标准化速度，vc为实际速度。在本实施例中，vn取值为80km/h。

经过对轮胎/路面声压级进行速度的干扰抑制处理后，路面构造深度的计算公式为：

ymtd＝p(y|θ,k)·ln(14)

使用公式(14)计算出来的路面构造深度的，消除了行车速度对轮胎/路面噪声信号的干扰，使计算结果更加准确。

实施例3

本发明提供了一种基于声学信号的路面构造深度检测装置，包括：声音采集单元、数据传输单元、计算单元和控制单元；

声音采集单元用于采集声学信号，数据传输单元用于将声学信号传输给计算单元，计算单元用于根据声学信号计算路面构造深度，控制单元用于控制音频采集单元、数据传输单元和计算单元工作。

以下对实施例3工作原理进行详细说明：

声音采集单元包括多个声音传感器，在本实施例中，声音传感器选用麦克风，麦克风的数量至少为2个。这2个麦克风分别安装于车辆轮胎旁侧，安装方式不作限定，可参照实施例1中的安装方式进行安装。

在本实施中，控制单元和计算单元均可集成在工控机中。当检测装置开始工作后，控制单元控制声音采集单元进行声音采集；采集到的声音数据通过数据传输单元传输给计算单元。因在检测过程中车辆是出于行驶状态的，而麦克风是靠近轮胎的，如果采用有线传输方式并不便于走线安装，所以在本实施例中，数据传输单元是采用采用无线传输的方式进行将声音信号传输给计算单元。无线传输的方式不作限定，可以采用现有的任意一种无线传输方式，比如：wifi、4g等。

计算单元包括处理器和存储器；存储器用于存储本发明实施例1中方法所对应的程序，处理器被配置为执行存储器中存储的程序。计算单元接收到声音信号数据后，将数据存储在存储器中。然后由处理器调用存储器中预存的程序以及声音信号数据，通过处理器中嵌入式数字信号处理程序进行声音信号的a计权滤波处理，加窗滑动傅里叶变换，速度影响消除处理，主成分分析，再将第一主成分分量将输入到预先构建好的非线性混合高斯模型中，获取非线性混合高斯模型的输出，作为路面构造深度。

最后应说明的是：以上各实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述各实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的范围，其均应涵盖在本发明的权利要求和说明书的范围当中。