一种高比例可再生能源电力系统的次同步振荡辨识方法与流程

本发明属电力系统领域，更为具体地讲，涉及一种高比例可再生能源电力系统的次同步振荡辨识方法。

背景技术：

近年来，随着可再生能源发电的日益普及，次同步振荡现象时有发生。与传统的汽轮发电机扭振动力学引起的次同步振荡不同，它局限于系统的某一区域，发生在可再生能源电力系统中的次同步振荡涉及多种元件，并将扩展到很大的范围。在这些事故中，次同步振荡变得如此具有破坏性，威胁到设备的安全和系统的稳定运行。因此，对次同步振荡的监测和辨识对于制定及时有效的缓解次同步振荡的策略至关重要。

为了开发有效的次同步振荡辨识方法，人们做了一些努力。这些方法可以分为两类：非基于非离散傅里叶变换(dft)的方法和基于dft的方法。非dft方法一般采用模态分解或基于模型的参数辨识技术。例如，hilbert-huang变换通过经验模态分解(emd)将信号分解为一组固有模态函数，然后通过hilbert变换提取每个本征模态函数(imt)的信息。然而，在emd分解过程中经常会出现频谱混叠现象，无法准确地检测出间谐波。变分模态分解是一种确定相关频带并同时估计其相应模态的自适应方法。这些模态分解技术可以提取出各模态的参数，但计算量大。另一方面，prony方法、利用旋转不变性技术估计信号参数和粒子群优化是众所周知的基于模型的技术。这些方法要求对模型有先验知识，更适合于电能质量分析。

另一种辨识次同步振荡的方法是基于dft。例如，基于dft的迭代算法是为了克服混叠效应；为了克服栅栏效应，提出了插值算法；为了抑制多个正弦信号之间的干扰，提出了一种压缩感知(cs)dft方法，该方法首先获取静态相量，然后进行参数辨识。为了实现动态参数估计，进一步提出了基于泰勒展开的cs-taylor-fourier多频技术。

然而，这些研究需要瞬时数据进行计算。由于这些数据只存储在故障录波器中，因此需要花费时间和精力来收集它们，因此这些方法不适合在实际电力系统中进行在线监测。一种更有吸引力的方法是基于同步相量数据。与监控与数据采集系统(scada)相比，包括广域测量系统(wams)在内的同步测量技术以更高的报告率实现了同步相量测量。相量测量单元(pmu)作为wams的测量单元，已经覆盖了大多数输电网络和发电厂，广泛应用于大型电力系统的动态监测，是一个很有前途的次同步振荡监测平。然而，由pmu提供的同步相量数据是ieee标准中定义的基频分量的相量，次同步振荡的特点是振荡发生在低于标称频率的频率上。通常，用于同步相量算法的pmu使用固定频率和固定窗口长度进行采样。因此，无论pmu的采样频率有多高，同步分量的非整周期都会引起频谱泄漏。主要问题是如何通过同步相量数据提供的有限信息来获取单点同步器的参数。因此，有必要对pmu数据采取一定的措施来辨识次同步分量。通过从pmu数据中恢复次同步振荡的信息来获取次同步振荡的频率。文献中的最新研究提出了一种利用pmu数据的频谱泄漏来辨识次同步振荡关键参数的方法。虽然该方法具有创新性和综合性，但在基频和同步频率相近的情况下，效果并不理想，且在噪声条件下鲁棒性较差。

技术实现要素：

本发明的目的在于克服现有技术的不足，提供一种高比例可再生能源电力系统的次同步振荡辨识方法，通过分析次同步振荡时加窗函数的同步相量的频谱特性，然后对同步相量采用三点插值法，得到次同步振荡的参数，实现次同步振荡的精准辨识。

为实现上述发明目的，本发明一种高比例可再生能源电力系统的次同步振荡辨识方法，其特征在于，包括以下步骤：

(1)、提取高比例可再生能源电力系统包含一个基波和一个次同步振荡分量的瞬时电流或电压信号x(t)：

其中，a1,f1,φ1和as,fs,φs分别表示基波和次同步分量的振幅、频率和相位，αs是次同步振荡的衰减因子，下标s表示次同步振荡；

(2)、以固定的采样频率fsampling对信号x(t)进行采样，并以报告率fr向主站传输，主站得到采样后的离散信号x(n)，n为采样个数；

其中，fp1＝f1/fp，fps＝fs/fp分别是基波和次同步振荡分量的归一化频率，αps＝αs/fp是衰减因子的归一化形式，fp＝fsampling/fr是采样间隔；

(3)、加窗的离散傅里叶变换；

设加入的hann窗的离散形式为：

其中，np＝fp/f0为hann窗的窗长度，f0是电力系统的标称频率；

对x(n)进行加窗的离散傅里叶变换，得到xw(k)：

(4)、提取离散傅里叶频谱xw(k)中第m个滑窗处的频谱；

其中，l1＝fp1×np，ls＝fps×np分别为基波频率和次同步振荡频率在频域归一化后的位置；

(5)、基于频谱xw(m,k)，提取基波分量x1和次同步振荡分量xs；

(6)、基于欧拉公式和级数求和公式，化简基波分量x1和次同步振荡分量xs；

x1化简为：

其中，(·)^*是复数共轭符号，w1(·)表示hann窗函数基波分量的离散傅里叶变换形式，表达式为w1(λ)＝-0.25wr(λ-1)+0.5wr(λ)-0.25wr(λ+1)，wr(·)是矩形窗函数的频谱，表达式为

xs化简为：

其中，ws(·)表示hann窗函数次同步振荡分量的离散傅里叶变换形式，表达式为ws(δ)＝-0.25wr(δ-1)+0.5wr(δ+1)+wr(δ+1)，

(7)、忽略负频谱部分对频谱的影响，通过pmu得到的同步相量xp：

(8)、通过同步相量，利用加hann窗的离散傅里叶插值法辨识的次同步振荡参数fs、αs和as；

(8.1)、计算频谱xs中相应频谱幅值比值r1和r2；

其中，k2是频谱的最高点位置，v(k2)是相应的幅值，k3和k1是频谱的第二高和第三高点位置，v(k3)与v(k1)是第二和第三高的频谱幅值；

(8.2)、计算次同步振荡频率fs：

(8.3)、计算次同步振荡衰减因子αs：

(8.4)、计算次同步振荡幅值as：

本发明的发明目的是这样实现的：

本发明一种高比例可再生能源电力系统的次同步振荡辨识方法，通过相量测量单元测得同步相量数据，分析发生次同步振荡时同步相量的特性，得到同步相量与基波频谱和次同步振荡频谱的线性关系，然后采用三点插值法对频域下的同步相量精确识别，得到次同步振荡的频率、阻尼因子和幅值等参数。

同时，本发明一种高比例可再生能源电力系统的次同步振荡辨识方法还具有以下有益效果：

(1)、本发明不需要任何关于振荡或电力系统模型的先验知识，直接对高比例可再生能源电力系统的次同步振荡进行辨识。

(2)、本发明在同步相量数据上采用加窗插值的方法进行次同步振荡的参数辨识，具有操作简单，计算复杂度小等特点。

(3)、通过在非标称、噪声等不同情况下的测试，结果表明，在大多数情况下，参数辨识的偏差小于1％，频率辨识的偏差小于10^-4％，具有辨识精度高的特点。

附图说明

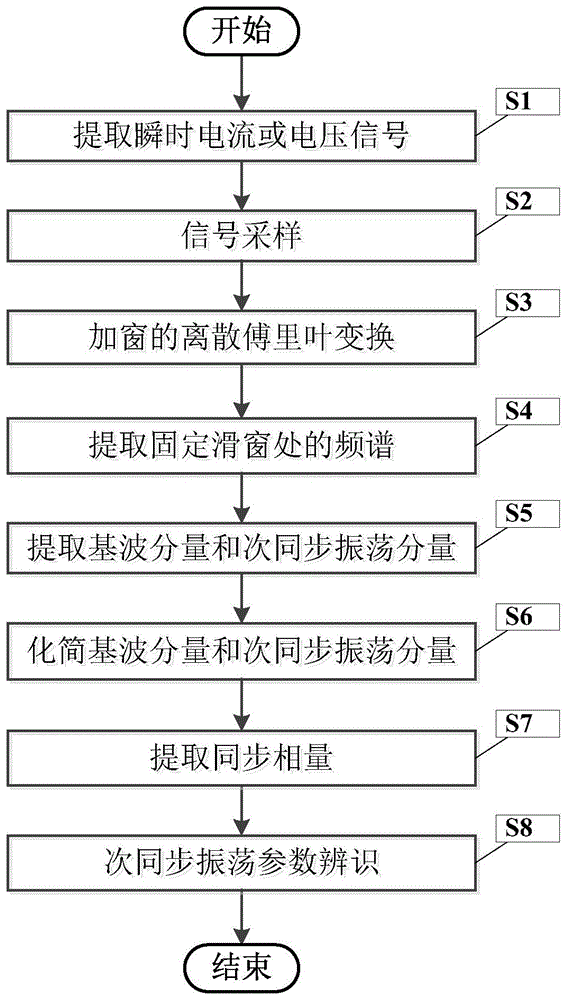
图1是本发明一种高比例可再生能源电力系统的次同步振荡辨识方法流程图；

图2是在参数fs的影响下各个参数辨识结果图；

图3是在参数αs的影响下各个参数辨识结果图；

图4是在参数as的影响下各个参数辨识结果图；

图5是在参数fs的影响下施加噪声影响后各参数的估计偏差图；

图6是在参数αs的影响下施加噪声影响后各参数的估计偏差图

图7是在参数as的影响下施加噪声影响后各参数的估计偏差图。

具体实施方式

下面结合附图对本发明的具体实施方式进行描述，以便本领域的技术人员更好地理解本发明。需要特别提醒注意的是，在以下的描述中，当已知功能和设计的详细描述也许会淡化本发明的主要内容时，这些描述在这里将被忽略。

实施例

图1是本发明一种高比例可再生能源电力系统的次同步振荡辨识方法流程图。

在本实施例中，如图1所示，本发明一种高比例可再生能源电力系统的次同步振荡辨识方法，包括以下步骤：

s1、提取高比例可再生能源电力系统包含一个基波和一个次同步振荡分量的瞬时电流或电压信号x(t)：

其中，a1,f1,φ1和as,fs,φs分别表示基波和次同步分量的振幅、频率和相位，αs是次同步振荡的衰减因子，下标s表示次同步振荡；

s2、以固定的采样频率fsampling对信号x(t)进行采样，并以报告率fr向主站传输，主站得到采样后的离散信号x(n)，n为采样个数；

其中，fp1＝f1/fp，fps＝fs/fp分别是基波和次同步振荡分量的归一化频率，αps＝αs/fp是衰减因子的归一化形式，fp＝fsampling/fr是采样间隔；

s3、加窗的离散傅里叶变换；

众所周知，基于dft的同步相量估计算法有两个主要误差源：1)混叠和2)频谱泄漏。混叠通常通过两种方法进行纠正：1)使用抗混叠滤波器或2)将采样频率增加到远大于采样信号中包含的最高频率分量的值。另一方面，如上所述，频谱泄漏问题是由于采样过程中被分析信号的基频和额定频率之间的差异引起的，已经采用了几种方法来减小这种偏差。这些方法主要涉及：1)窗口函数，其目的是减少频谱泄漏的影响。如果加窗不能很好地补偿泄漏，当且非常接近时，二者之间会产生相互作用，从而产生误差，即所谓的频谱干扰和2)合适的dft插值方案，目的是校正短距离泄漏的影响，降低dft频率引起的不精确性结果。

基于这些考虑，本发明采用了两种方法来减少前面描述的误差源：1)加hann窗函数，2)dft插值。

设加入的hann窗的离散形式为：

其中，np＝fp/f0为hann窗的窗长度，f0是电力系统的标称频率，也就是50hz或者60hz；

对x(n)进行加窗的离散傅里叶变换，得到xw(k)：

其中，k是频谱区间数，j是复数单位；

s4、提取离散傅里叶频谱xw(k)中第m个滑窗处的频谱；

其中，l1＝fp1×np，ls＝fps×np分别为基波频率和次同步振荡频率在频域归一化后的位置；

s5、基于频谱xw(m,k)，提取基波分量x1和次同步振荡分量xs；

s6、基于欧拉公式和级数求和公式，化简基波分量x1和次同步振荡分量xs；

x1化简为：

其中，(·)^*是复数共轭符号，w1(·)表示hann窗函数基波分量的离散傅里叶变换形式，表达式为w1(λ)＝-0.25wr(λ-1)+0.5wr(λ)-0.25wr(λ+1)，wr(·)是矩形窗函数的频谱，表达式为

xs化简为：

其中，ws(·)表示hann窗函数次同步振荡分量的离散傅里叶变换形式，表达式为ws(δ)＝-0.25wr(δ-1)+0.5wr(δ+1)+wr(δ+1)，

s7、负频谱影响的相关成为表示为：

可以看出x1和xs的频谱主要有两部分组成，主瓣和相应的负谱尾。考虑到实际上fp＞＞f0并且使用了hann窗，负频谱成分γ+ω对整个频谱的影响可以忽略。因此，当发生次同步振荡时，通过pmu得到的同步相量xp：

s8、xp包含基频和次同步两个分量，在频域下次同步分量和基波分量成线性叠加关系，因此本发明通过同步相量，利用加hann窗的离散傅里叶插值法辨识的次同步振荡参数fs、αs和as；

s8.1、计算频谱xs中相应频谱幅值比值r1和r2；

其中，k2是频谱的最高点位置，v(k2)是相应的幅值，k3和k1是频谱的第二高和第三高点位置，v(k3)与v(k1)是第二和第三高的频谱幅值；

s8.2、计算次同步振荡频率fs：

s8.3、计算次同步振荡衰减因子αs：

s8.4、计算次同步振荡幅值as：

至此，次同步振荡所有的关键参数包括频率、衰减因子和幅值都由同步相量中的信息辨识得到。

实例验证

为了便于本领域人员理解发明的技术内容以及技术性能，下面结合附图对本发明内容和性能进一步阐释。提取高比例可再生能源电力系统包含一个基波和一个次同步振荡分量的瞬时电流或电压信号x(t)，经过以上分析，次同步振荡参数辨识基于上报的同步相量在频域的信息。通常对于50hz的电力系统，pmu由两种上报频率，fr＝f0或fr＝2f0。考虑到50hz上报频率情况下，根据采样定理，同步相量不能辨识频率fs＞f0/2的次同步振荡，因此设置pmu上报频率fr为100hz。采样频率fsampling设置为10000hz，窗长np为200，这意味着同步相量数据频率间隔为100hz，频率分辨率为0.5hz。在接下来的部分，因为辨识误差ep来评估所提出方法的准确度，计算公式为：

其中，和p分别为参数的辨识值和真实值。为了验证方法在不同条件下的性能，研究了参数对辨识结果的影响。

1)、fs的影响；

设置信号参数为a1＝100、as＝10、φ1＝π/9、φs＝π/35和αs＝0.15。通常电力系统频率浮动范围不超过基频的2％，因此，基频在标称和非标称的五种频率即49.1,49.5,49.7,50,50.3,50.5,50.9hz测试。fs变化范围是[10,45]hz，步长为0.5hz。各个参数辨识结果如图2所示，其中，图2中(a)为频率辨识偏差结果，(b)为衰减因子辨识偏差结果，(c)幅值辨识偏差结果。可以看出，当基频f1＝49.5,50和50.5hz时的辨识误差比其他情况下小，结果曲线几乎重合；当fs接近15,25和35hz时，辨识误差为极小值，表明在频率分辨率为整数的情况下，这三个频率的识别结果更加准确。随着fs接近f1，辨识误差由于频谱泄露逐渐增大。尽管如此，三种参数的辨识误差保持在1％以下的水平。

2)、αs的影响；

设置信号参数为a1＝100、as＝10、φ1＝π/9和φs＝π/35。为防止采样频率与次同步频率相干，fs设为27.25hz。αs变化范围是[0.01,1]步长为0.01。结果如图3所示，各个参数辨识结果如图3所示，图3中(a)为频率辨识偏差结果，(b)为衰减因子辨识偏差结果，(c)幅值辨识偏差结果。可以看出，αs变化对频率和幅值的识别影响不大，但对阻尼因子的估计有影响。其原因是当αs变大时，次同步部分在频谱中变得更加明显。与第一种情况一样，由于频谱泄漏，在非标称频率下，三个参数的估计偏差较大。

3)、as的影响；

设置信号参数为a1＝100、αs＝0.25、fs＝27.25、φ1＝π/9和φs＝π/35。as变化范围是[5,50]步长为5。辨识结果如图4所示，各个参数辨识结果如图4所示，图4中(a)为频率辨识偏差结果，(b)为衰减因子辨识偏差结果，(c)幅值辨识偏差结果。可以看出随着振荡幅值的增长，三种参数辨识误差呈现相同地趋势。当f1＝49.5,50和50.5hz时，as变化对估计结果影响不大时，在其他频率下，估计偏差随频率的增加而减小。一般来说，在这种情况下，辨识结果低于0.1％。

4)、噪声的影响；

算法对噪声的敏感性是评价识别技术性能的重要指标。根据文献显示，实际数据中的信噪比(snr)约为45db。其中snr定义为：

其中，σ²是高斯白噪声的方差。

在本实施例中，在前三个实验中分别加入了40db和20db的高斯白噪声进行重做，图5、6和7中，展示出了噪声条件下三个参数的估计偏差。图5、6、7中的(a)、(b)、(c)分别为噪声在40db下的频率、衰减因子、幅值辨识误差，(d)、(e)、(f)为噪声在20db下的频率、衰减因子、幅值辨识误差，可以看出，频率辨识误差在10^-4％左右，衰减因子误差在1％左右，幅值辨识误差为0.1％至0.01％；结果表明：1)、噪声降低了参数估计的精度，噪声条件下参数变化对估计精度的影响不明显。2)、在有噪声情况下，与阻尼因子和幅值相比，频率的估计偏差仍然最小。3)、在大多数噪声情况下，估计偏差小于1％，意味着本方法在含有噪声情况下的鲁棒性高。

综上所述，本发明提出了一种基于同步相量的次同步振荡参数辨识技术，以准确获取电压、电流信号中的次同步振荡参数。通过对模拟信号的测试表明，在大多数情况下都能保持较高的精度，特别是对次同步频率的识别，即使是在非标称和噪声情况下。该方法不仅可以增强pmu设备的性能，而且可以实现对实际高比例可再生能源电力系统次同步振荡事件的监测。

尽管上面对本发明说明性的具体实施方式进行了描述，以便于本技术领域的技术人员理解本发明，但应该清楚，本发明不限于具体实施方式的范围，对本技术领域的普通技术人员来讲，只要各种变化在所附的权利要求限定和确定的本发明的精神和范围内，这些变化是显而易见的，一切利用本发明构思的发明创造均在保护之列。