正弦调频干扰下基于子相关函数的CBOC信号无模糊捕获算法

正弦调频干扰下基于子相关函数的cboc信号无模糊捕获算法
技术领域
1.本发明属于导航通信中cboc信号捕获的相关领域，具体为在正弦调频干扰下基于子相关函数的cboc信号的无模糊捕获算法。


背景技术：

2.近年来，全球导航卫星系统(global navigation satellite systems，gnss)广泛应用于军事和民用领域，因此越来越多的卫星导航系统被研制出来，如美国政府管理的全球定位系统(global position system，gps)，欧盟及欧洲航天局管理的伽利略卫星导航系统(galileo satellite navigation system，galileo)，俄罗斯联邦政府管理的全球卫星导航系统(global navigation satellite system，glonass)，我国政府管理的北斗卫星定位通信系统(beidou navigation satellite system， bds)，印度政府管理的区域导航定位系统(india regional navigation satellitesystem，irnss)等。这使得导航频段变得越来越拥挤。在这样的背景下，boc 及其衍生信号因为其频谱分裂的特性可以实现新老业务的兼容，而被广泛应用于新一代的导航卫星系统中。然而，在实际的应用场合中，接收到的boc信号由于传播路径远和接收功率小，而经常受到各种干扰。作为boc信号的衍生信号，cboc信号虽然有更强的抗干扰能力，但是在强干扰下其频谱依旧会发生失真现象导致其无法被精确捕获。所以研究boc及其衍生信号在各种干扰环境下的接收性能，并提出有效可行的抗干扰捕获方法具有重要的意义和价值。
3.针对正弦调频干扰下cboc信号频谱发生严重失真，导致其无法被捕获的问题，提出了一种将正弦调频变换结合子相关函数的无模糊捕获算法，该方法可以实现正弦调频干扰下cboc信号的无模糊捕获，文献“窄带干扰环境下的 boc信号捕获”提出了一种基于频域fft重叠变换窄带干扰抑制方法和相关重构方法相结合的boc捕获算法。该算法首先通过对信号重叠加窗处理，降低信号的频谱泄露和减小信号的损失，然后通过频域陷波技术对干扰信号进行有效的抑制，最后将经过处理后的boc信号利用相关重构方法进行捕获。文献“基于分数阶傅里叶变换的gnss接收机抗线性调频干扰技术研究”采用frft抑制宽带线性调频干扰，再采用frft对后续信号进行捕获。但是上述两篇文献主要针对窄带干扰和宽带干扰，很少有研究针对正弦调频干扰，对于无模糊捕获算法，最常用的是pcf分析方法，pcf方法的主要思想是通过引入两个特别设计的本地码来生成一个主峰宽度与boc信号自相关函数主峰宽度相同的单峰相关函数，因此保留了boc信号窄主峰的特性。如文献“boc及其衍生信号通用无模糊捕获分析”，提出了一种基于伪相关函数(pseudo correlation function，pcf) 的无模糊捕获改进方法。首先，根据形状码向量的概念构建了boc信号的互相关函数统一表达式，并提出了两组新的形状码向量；然后，通过接收信号与形状码向量对应的参考信号作互相关合成得到一个单峰；最后，通过单峰与自相关函数合成得到无模糊捕获方法。但是此算法仅仅只能对无干扰环境下的boc 及其衍生信号进行捕获，对正弦调频干扰下是否还能捕获还需进一步的验证。


技术实现要素：

4.本发明所要解决的技术问题，正弦调频干扰下接收机的接收信号频谱完全失真，所以传统的算法无法对其进行捕获。对于正弦调频干扰可以使用正弦调频变换对其进行干扰抑制，对于捕获算法的情况，可以使用一种基于子相关函数组成相关函数的捕获算法，针对以上问题，本文提出了一种基于正弦调频变换和子相关函数相结合的无模糊捕获算法。
5.本发明解决上述技术问题的技术方案是：在正弦调频干扰下基于正弦调频变换和子相关函数相结合的cboc信号无模糊捕获算法，其步骤在于，首先通过正弦调频变换实现对正弦调频干扰的抑制，因为正弦调频干扰信号会在 dsfmt域聚拢，所以通过这一特征可以判断干扰位置并置零从而实现正弦调频干扰的抑制，然后把经过伪码调制的副载波分为12个组，将干扰抑制处理后的接收信号和这12组子副载波进行相关得到12组子相关函数，再根据12组子相关函数之间的对应关系按照一定的代数关系式合成仅有主峰的相关函数，最后将相关函数的最大值和预设门限做比较，若超过门限说明捕获成功，如果没有超过门限，调整组合扩频码继续上述操作。需要注意的是，所分组数为12的整数倍即可，同时所分组数越多，其主峰会越窄，性能会越好。
6.本发明将正弦调频变换和子相关函数相融合，并应用到了正弦调频干扰下 cboc信号的捕获过程中，详细介绍了cboc信号的模型，推导了子相关函数合成相关函数完成cboc信号的无模糊捕获原理，以及该方法实现的具体步骤，验证了正弦调频变换抑制正弦调频干扰的有效性，克服了正弦调频干扰下传统捕获方法无法完成cboc信号的捕获，综上所述，本发明在实际的cboc信号捕获中具有重大意义。
附图说明
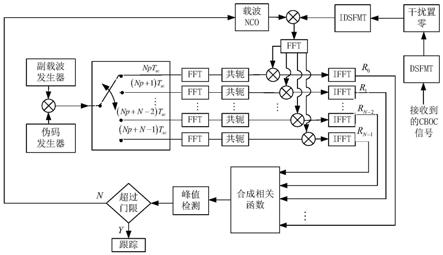
7.图1本发明的正弦调频干扰下cboc信号的无模糊捕获原理框图；
8.图2本发明的含正弦调频干扰的cboc信号的dsfmt域谱图
9.图3本发明的cboc(6,1,1/11)信号子载波分解图
10.图4本发明的cboc(6,1,1/11)的子相关函数
11.图5本发明的cboc(6,1,1/11)组合后的相关函数
12.图6本发明的cboc(6,1,1/11)干扰抑制前后频谱对比
13.图7本发明的不同算法归一化幅度输出对比
14.图8本发明的不同分组数下归一化幅度输出对比
15.图9本发明的不同算法的主峰比例均值对比
16.图10本发明的不同分组数下主峰比例均值对比
具体实施方式
17.以下结合附图和具体实例，对本发明的实施作进一步的描述。
18.步骤一：图1所示为本发明正弦调频干扰下cboc信号的无模糊捕获算法实现的具体框图，具体步骤：首先对接收到的信号做正弦调频变换，通过正弦调频干扰信号在正弦调频变换下呈现聚拢状态这一特点确定正弦调频干扰的位置并进行置零处理从而达到正弦调频干扰的抑制，然后用振荡器振荡出载波信号，对cboc(6,1,1/11)调制信号进行解调，并对解调后的cboc(6,1,1/11)信号作fft变换处理。对本地伪码序列进行副载波二次调制。对
调制后的信号选取码片，截取所需的n个不同的码片，然后进行fft共轭运算，将共轭运算后的子信号与fft变换处理后的接收cboc(6,1,1/11)信号相乘，然后取ifft，得到 cboc(6,1,1/11)信号自相关函数的每一个子相关函数。将得到的子相关函数按照本文提到的捕获算法合成相关函数。将相关函数的最大值与阈值进行比较，若大于设定的阈值进入跟踪阶段，若小于阈值，重复以上步骤。
19.步骤二：图2所示即为含正弦调频干扰的cboc信号在dsfmt域的谱线，由图2可知，对含正弦调频干扰的cboc信号做dsfmt，cboc信号会在 dsfmt域聚拢，通过这一点可以得到干扰谱线的位置，并且进行干扰置零处理，再做idsfmt就可以得到cboc信号。
20.步骤三：cboc(6,1,1/11)信号子载波分解过程分析。cboc(6,1,1/11)信号的经过伪码调制的副载波表示为将其分为n＝12个部分，记其中一个子副载波对应的某个部分为其中l∈{0,1,2,
…
11}，具体的分解过程如图3所示。所以，副载波可以进一步表示为：
[0021][0022]
步骤四：cboc(6,1,1/11)信号的子相关函数形成分析。cboc(6,1,1/11)信号的归一化自相关函数可以表示为：
[0023][0024]
其中，λ
l
(τ)表示cboc(6,1,1/11)信号的某个部分的子相关函数。cboc(6,1, 1/11)信号子相关函数有12个，前6个如图4(a)所示，后6个如图4(b)所示。
[0025]
步骤5：利用子相关函数合成无模糊的相关函数过程分析。根据图4(a)和4(b) 可知，这12个子相关函数都是由不同相位的子载波组成，每个子载波的相关值都有正有负，并且存在对称关系，即：
[0026]
r
l
(τ)＝r
n-1-l
(τ)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0027]
通过伪相关函数法(pcf)得到代数思路，
[0028][0029]
可以得到关系式：
[0030][0031]
将cboc(6,1,1/11)信号的子相关函数按式(5)结合，得到的图形如图5 所示。
[0032]
根据图5，组合后的相关函数都为正，并且最后一个图的主峰值最窄，根据这些特征可以得到最后的相关函数为：
[0033][0034]
步骤六：图6为cboc(6,1,1/11)干扰抑制前后频谱对比。由图6可知， cboc(6,1,1/11)信号在sfm干扰下的频谱严重失真，这一点有极大的可能性导致cboc(6,1,1/11)信号无法精确的捕获，而经过sfm干扰抑制后的cboc(6,1,1/11)频谱和原cboc(6,1,1/11)频谱相比相差不大，说明本发明算法可以很好的抑制cboc(6,1,1/11)信号中的sfm干扰为后面cboc(6,1,1/11)的捕获提供一个相对较好的环境。
[0035]
图7为不同算法归一化幅度输出对比。由图7可以看出cboc(6,1,1/11)信号的自相关函数具有多峰的特点，副峰会造成捕获的模糊性，通过aspect算法和scpc算法可以基本消除自相关函数的模糊性，但是副峰清除的不够充分，还是会造成一定程度上的误捕，而本发明的算法不仅完全消除了副峰，而且主峰的宽度比其自相关函数，aspect算法和scpc算法的主峰宽度都窄，说明本文算法的性能是这四类算法中是最优的。
[0036]
图8为被伪码调制的副载波所分不同组数输出的归一化幅度。由图8可知，本发明的算法完全的消除了副峰，当副载波分的部分越多其主峰的宽度越窄。如：副载波分为24组的主峰宽度是副载波分为12组的主峰宽度的二分之一，副载波分为48组的主峰宽度是副载波分为24组的主峰宽度的二分之一，副载波分为36组的主峰宽度界于副载波分为24组和副载波分为48组的主峰宽度之间。
[0037]
图9为不同算法下的主峰比例均值对比，由图9可以看出，干扰抑制前的主峰比例均值基本都为0，这是因为正弦调频干扰下cboc(6,1,1/11)信号的频谱严重失真，导致传统的无模糊捕获算法无法对其进行捕获，对于干扰抑制后本文算法的主峰比例均值大于aspect算法和scpc算法，这说明本发明算法的性能优于aspect算法和scpc算法。
[0038]
图10为分组数不同时主峰比例均值对比，由图10可以看出，当被伪码调制的副载波所分成子载波的数目越多，其主峰比例均值就越大，主峰比例均值越大就意味着该算法的性能越好，但是随着副载波分组数的增多，其计算复杂度也会增大，所以在实际的应用中可以先考虑系统的需求，再确定需要将副载波分为多少组。