基于非线性压电效应预测压电陶瓷剪切运动位移的方法与流程

本发明涉及一种预测压电陶瓷位移的方法，尤其是基于非线性压电效应预测压电陶瓷剪切运动位移的方法，属于压电陶瓷驱动技术领域。

背景技术：

压电陶瓷驱动器是精密定位系统中重要的主动单元，其主要是依靠多晶压电陶瓷材料的逆压电效应来实现电能向机械能的转化，而这种材料特性行为可由压电本构方程来描述。在压电本构方程中，力-电耦合作用的纽带是压电常数，其可以定量地评价能量的转化过程。目前，在大多数基于压电陶瓷驱动的精密定位机构的研究中，常将压电常数取为定值，从而用线性关系来描述驱动电压实现的位移转化量。然而，随着微小型化技术的快速发展，人们对压电驱动技术也不断地提出更高的要求，以获得更大的位移、更高的振动频率。例如，随着振动辅助切削技术在切削加工中从起初的改善切削条件到现在的实现织构化功能表面的加工，压电驱动器所提供的刀具运动轨迹从起辅助作用而转变为起决定微结构形状尺寸的主导作用，这就需要刀具有更精准的运动轨迹和更大的运动幅度。但是，当压电陶瓷材料内部的电场强度超过某一阈值时，其内部非180度畴壁的运动会导致最终的应变量不再随电场线性相关，也就是压电常数不再为定值而是依赖电场强度变化的。此外，当交变电场的频率较高时，电畴的运动会跟不上电场的快速变化，从而也不再遵循线性的压电效应。因此，考虑压电陶瓷材料的电场及其频率的依赖相关作用，建立相应的本构方程，实现对其在高压高频激励下的位移预测具有重要的研究意义。

通常在压电陶瓷的纵向、横向以及剪切三种机械变形中，压电剪切常数的数值最大，故在相同电压条件下压电陶瓷剪切变形能够输出最大的位移，同时压电剪切叠堆能够直接提供水平位移和弯曲变形，故有很大的应用潜力。对现有技术文献总结发现，文献“shearresponseofleadzirconatetitanatepiezoceramics”，muller和zhang，journalofappliedphysics,1998,83(7):3754-3761，该文献提出了压电剪切常数随电场的指数变化关系，得到了考虑电场相关的非线性压电方程。文献“logarithmicfrequencydependenceofthepiezoelectriceffectduetopinningofferroelectric-ferroelasticdomainwalls”damjanovic,physicalreviewb,1997,55(2):r649-r652，该文献研究发现压电纵向常数与指数频率有线性相关性。然而，目前现有的研究中还没有同时考虑电场及其频率对压电常数的影响，以实现对压电陶瓷在高压和高频激励下进行位移预测。

技术实现要素：

本发明的目的是为了解决压电陶瓷剪切叠堆驱动器在开环工作模式下受激励电场强度及频率变化的影响而表现出的位移非线性的行为，而目前现有压电陶瓷材料的本构模型没有同时考虑电场强度及其频率的依赖性，进而提供基于非线性压电效应预测压电陶瓷剪切运动位移的方法，以实现对压电陶瓷剪切叠堆驱动器动态位移的准确预测。

为实现上述目的，本发明采取下述技术方案：基于非线性压电效应预测压电陶瓷剪切运动位移的方法，包括以下步骤：

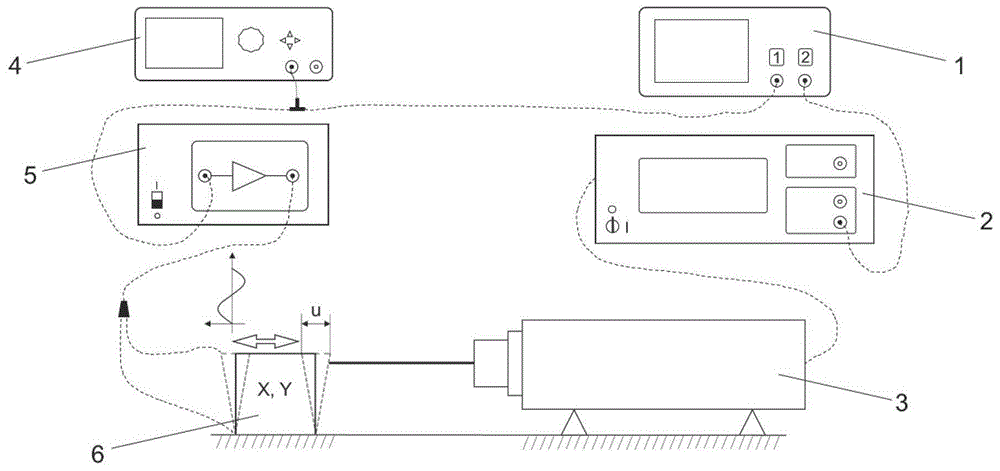
步骤一：搭建压电陶瓷剪切叠堆位移测量平台

测量平台包括示波器、测振仪控制器、激光多普勒测振仪、信号发生器、电压放大器及压电陶瓷剪切叠堆，所述信号发生器产生正弦交变电压信号，并通过所述电压放大器放大以达到驱动压电陶瓷剪切叠堆的电压要求，此时所述压电陶瓷剪切叠堆开始简谐往复平移，其底部固定，上部为自由运动端，通过调节信号发生器的输出信号，实现对压电陶瓷剪切叠堆运动幅度及频率的控制，采用所述激光多普勒测振仪对压电陶瓷剪切叠堆的动态位移进行测量，测量的位移信号通过所述测振仪控制器转化为电压信号以供示波器进行采集，所述示波器在采集位移信号的同时采集信号发生器的输出信号，以比较激励信号和响应信号的相位差，分析压电陶瓷剪切叠堆的压电效应的响应状态；

步骤二：获得压电陶瓷剪切叠堆遵循压电效应的最大响应频率

基于压电陶瓷的逆压电效应，以正弦变化信号为激励，在恒定激励电压情况下，测量压电陶瓷剪切叠堆随激励频率逐渐增大的动态位移响应，计算激励信号与响应信号的相位差，得到压电陶瓷材料遵循压电效应的最大响应频率；

步骤三：测量不同电压和频率下压电陶瓷剪切叠堆的位移

在步骤二中获得的最大响应频率和压电陶瓷剪切叠堆的额定电场的范围内，测量压电陶瓷剪切叠堆在不同电压和频率激励下的位移量，获得与电压及频率相对应的位移实验数据；

步骤四：拟合提出的非线性压电本构方程

提出了同时考虑电场强度及频率依赖相关的非线性压电陶瓷剪切压电本构方程：

d15(e1，f)＝dlin(f)[1+(dnl(f)e1)^1.2](7)

dlin(f)＝a1ln(f)+b1(8)

dnl(f)＝a2ln(f)+b2(9)

其中，s为压电陶瓷的应变量，t为外力导致陶瓷内部的应力，d为压电陶瓷的电位移量，e为施加的电场强度，ε为介电系数矩阵，s为弹性柔度矩阵，d15为压电剪切常数，dlin为压电剪切常数的线性系数，dnl为压电剪切常数的非线性系数，e1为垂直于极化方向的电场，f为交变压力的频率，a1和b1及a2和b2分别为线性方程的一次项系数和常数，

利用测得的实验数据对提出的压电本构方程进行拟合分析，确定公式(8)和公式(9)中a1，b1，a2，b2的数值，得到压电剪切常数d15随电场强度及其频率变化的压电本构方程完整表达式，

首先，对步骤三中测得的数据进行换算，电压换算成电场，位移换算成剪切应变，根据以下公式：

e1＝u1/t(10)

s＝u/t(11)

其中，u1为垂直于压电陶瓷极化方向施加的电压，t为压电陶瓷剪切片的厚度，u为剪切片所产生的位移量，

数据在压电叠堆不受外力的作用测得，故公式(6)中表示逆压电效应的部分可变为：

s＝d15·e1(12)

根据以上公式可以计算得到不同电压及不同频率的位移数据点所对应的压电剪切常数d15数值，在每个选定的频率f下，利用d15随电场e1变化的数据对公式(2)进行指数拟合，可以得到相应压电常数的线性系数dlin和压电常数的非线性系数dnl的估计值，通过对所有选定的频率进行如上的拟合计算，就可以得到不同频率下所对应的dlin和dnl的数值，以公式(8)和公式(9)为目标方程，以对数频率ln(f)为自变量，dlin和dnl为因变量进行线性拟合，就可得到dlin和dnl随频率f变化的表达式，之后带入到公式(7)中，并与公式(6)联立，得到考虑电场强度及其频率影响的压电陶瓷剪切压电本构方程；

步骤五：向本构方程输入期望的激励条件得到位移预测值

通过向该方程输入电场及其频率，就能得到压电陶瓷相应的剪切应变量，进而即可实现对压电陶瓷剪切运动位移进行预测。

与现有技术相比，本发明的有益效果是：本发明考虑了电场强度及频率影响的压电陶瓷本构方程的建立方法，可在高频/高压情况下预测压电陶瓷剪切叠堆驱动器的动态位移，本发明的非线性压电本构方程能够描述压电陶瓷材料在交变力-电联合载荷作用下正压电效应和逆电效应的耦合行为，对提高压电驱动器在复杂工作环境下运动精度的控制具有重要的意义。

附图说明

图1是本发明所搭建的测量平台的示意图；

图2是本发明具体实施方式中实例陶瓷叠堆在同一电压的不同交变频率下的动态响应示意图；

图3是本发明具体实施方式中实例陶瓷叠堆在不同电压及不同频率下测量得到的位移量示意图；

图4是本发明具体实施方式中实例陶瓷叠堆线性拟合频率相关的压电剪切常数的线性系数和非线性系数。

具体实施方式

下面将结合本发明实施例中的附图，对本发明中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅是发明的一部分实施例，而不是全部的实施例，基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明公开了基于非线性压电效应预测压电陶瓷剪切运动位移的方法，包括以下步骤：

步骤一：搭建压电陶瓷剪切叠堆位移测量平台

如图1所示，测量平台包括示波器1、测振仪控制器2、激光多普勒测振仪3、信号发生器4、电压放大器5、压电陶瓷剪切叠堆6，通过信号发生器4产生低压的正弦交变电压信号，低压的正弦交变电压信号通过电压放大器5放大以达到驱动压电陶瓷剪切叠堆6的电压要求，此时压电陶瓷剪切叠堆6开始简谐往复平移，其中，压电陶瓷剪切叠堆6的底部固定，上部为自由运动端，通过调节信号发生器4的输出信号，实现对压电陶瓷剪切叠堆6运动幅度及频率的控制，采用激光多普勒测振仪3对压电陶瓷剪切叠堆6的动态位移进行测量，测量的位移信号通过测振仪控制器2转化为电压信号以供示波器1进行采集，示波器1在采集位移信号的同时采集信号发生器4的输出信号，以比较激励信号和响应信号的相位差，分析压电陶瓷剪切叠堆6的压电效应的响应状态；

步骤二：获得压电陶瓷剪切叠堆遵循压电效应的最大响应频率

基于压电陶瓷的逆压电效应，以正弦变化信号为激励，在恒定激励电压情况下，测量压电陶瓷剪切叠堆6随激励频率逐渐增大的动态位移响应，计算激励信号与响应信号的相位差，得到压电陶瓷材料遵循压电效应的最大响应频率。

通常情况下，极化后的压电陶瓷会有确定的最大工作电压，而对于工作电压的频率往往没有提及。众所周知，过高的交变电场频率会导致压电陶瓷内部更少的电畴跟得上电场的变化，从而使得压电陶瓷的压电效应逐渐失效。而本发明是基于压电陶瓷材料本构方程实现对压电陶瓷的位移预测，故确定压电陶瓷遵循压电效应的最大响应频率非常有必要。具体的是：

在激励信号的电压固定的条件下，逐渐增大频率，记录压电陶瓷剪切叠堆6的电压激励信号及位移响应信号。下面结合实例：noliac公司生产的型号nac2902-h2.8的一维压电剪切叠堆，叠堆的长宽高尺寸为5*5*2.8mm，压电剪切片的厚度为0.5mm，最大驱动电压为±320v，最大运动范围为1.5μm进行说明，以下简称实例陶瓷叠堆，如图2所示，表示实例陶瓷叠堆的位移及输入和输出信号的相位差随激励频率的变化，可以看出随着频率的增大，实例陶瓷叠堆的位移先逐渐减小，随后迅速增大，拐点出现在3000hz左右，而相位差随着频率的增大，先趋于恒定，而达到一定频率后开始减小，拐点也出现在3000hz左右。相位差的改变说明输入信号与输出信号的对应关系发生了变化，也就是电压的峰-谷值不再对应实例陶瓷叠堆位移的峰-谷值，故不再遵循压电效应。因此，实例陶瓷叠堆压电效应的最大响应频率在3000hz附近；

步骤三：测量不同电压和频率下压电陶瓷剪切叠堆的位移

在步骤二中获得的最大响应频率和压电陶瓷剪切叠堆6的额定电场的范围内，测量压电陶瓷剪切叠堆6在不同电压和频率激励下的位移量，获得与电压及频率相对应的位移实验数据。

在步骤二中确定的最大电压及频率的范围内，以步骤二中的方式测量不同电压下，上述实例陶瓷叠堆随频率逐渐增大的位移变化，并记录电压和频率对应的位移量数据，如图3所示，为实例陶瓷叠堆在不同电压及不同频率下测量得到的位移量；

步骤四：拟合提出的非线性压电本构方程

结合现有描述压电陶瓷材料非线性压电效应的本构方程，建立以电场强度及频率依赖相关的非线性压电本构方程：

已提出的描述压电效应的线性本构方程为：

其中，s为压电陶瓷的应变量，t为外力导致陶瓷内部的应力，d为压电陶瓷的电位移量，e为施加的电场强度。此外，方程中反应材料性能的参数：d为压电常数矩阵，ε为介电系数矩阵，s为弹性柔度矩阵。

考虑电场强度对压电常数的影响，已提出的适合压电剪切常数的非线性表达式为：

d15(e1)＝dlin[1+(dnle1)^α](2)

其中，d15为压电剪切常数，dlin为压电剪切常数的线性系数，dnl为压电剪切常数的非线性系数，α指数通常取1.2，e1为垂直于极化方向的电场。

考虑交变频率对压电常数的影响，已提出的适合压电纵向常数的非线性表达式为：

d33(xmax)＝dinit+αxmax(3)

dinit(f)＝d0+dln(f)(4)

α(f)＝a0+aln(f)(5)

其中，d33为压电纵向常数，dinit和α为可逆和不可逆raileigh系数，xmax为交变压力的幅值，f为交变压力的频率，d0和d及a0和a为线性方程系数。

本发明将公式(3)中压电纵向常数d33随对数频率ln(f)线性变化的关系引入到公式(2)，并结合公式(1)，提出了同时考虑电场强度及频率依赖相关的非线性压电陶瓷剪切压电本构方程：

d15(e1，f)＝dlin(f)[1+(dnl(f)e1)^1.2](7)

dlin(f)＝a1ln(f)+b1(8)

dnl(f)＝a2ln(f)+b2(9)

其中，公式(7)为压电剪切系数对电场及其频率变化的表达式，a1和b1及a2和b2分别为线性方程的一次项系数和常数。

利用测得的实验数据对提出的压电本构方程进行拟合分析，确定公式(8)和公式(9)中a1，b1，a2，b2的数值，得到压电剪切常数d15随电场强度及其频率变化的压电本构方程完整表达式。

首先，对步骤三中测得的数据进行换算，电压换算成电场，位移换算成剪切应变，根据以下公式：

e1＝u1/t(10)

s＝u/t(11)

其中，u1为垂直于压电陶瓷极化方向施加的电压，t为压电陶瓷剪切片的厚度，u为剪切片所产生的位移量。

由于数据都是在压电叠堆不受外力的作用测得的，故公式(6)中表示逆压电效应的部分可变为：

s＝d15·e1(12)

故根据以上公式可以计算得到不同电压及不同频率的位移数据点所对应的压电剪切常数d15数值。在每个选定的频率f下，利用d15随电场e1变化的数据对公式(2)进行指数拟合，可以得到相应压电常数的线性系数dlin和压电常数的非线性系数dnl的估计值。通过对所有选定的频率进行如上的拟合计算，就可以得到不同频率下所对应的dlin和dnl的数值。以公式(8)和公式(9)为目标方程，以对数频率ln(f)为自变量，dlin和dnl为因变量进行线性拟合，就可得到dlin和dnl随频率f变化的表达式，如图4所示，为实例陶瓷叠堆得到的dlin和dnl随频率f变化的表达式：

dlin(f)＝-30.18ln(f)+650.4(13)

dnl(f)＝-0.04565ln(f)+1.361(14)

将公式(13)和公式(14)代入到公式(7)中，并与公式(6)联立，这样就最终得到了考虑电场强度及其频率影响的压电陶瓷剪切压电本构方程。

步骤五：向本构方程输入期望的激励条件得到位移预测值

通过向该方程输入电场及其频率，就能得到压电陶瓷相应的剪切应变量，进而即可实现对压电陶瓷剪切运动位移进行预测。

对于本领域技术人员而言，显然本发明不限于上述示范性实施例的细节，而且在不背离本发明的精神或基本特征的情况下，能够以其他的装体形式实现本发明。因此，无论从哪一点来看，均应将实施例看作是示范性的，而且是非限制性的，本发明的范围由所附权利要求而不是上述说明限定，因此旨在将落在权利要求的等同条件的含义和范围内的所有变化囊括在本发明内。不应将权利要求中的任何附图标记视为限制所涉及的权利要求。

此外，应当理解，虽然本说明书按照实施方式加以描述，但并非每个实施方式仅包含一个独立的技术方案，说明书的这种叙述方式仅仅是为清楚起见，本领域技术人员应当将说明书作为一个整体，各实施例中的技术方案也可以经适当组合，形成本领域技术人员可以理解的其他实施方式。