基于多GNSS的单频精密单点定位算法的时间频率传递方法与流程

本发明涉及基于导航卫星系统单频数据的高精度时间频率传递方法，具体涉及一种基于多个全球定位导航系统(gnss，包含gps、bds、galileo、glonass、qzss)的单频数据精密单点定位算法的时间频率传递方法。

背景技术：

当前高精度的时间频率传递主要有共视、全视、精密单点定位(ppp)方法与卫星双向比对(twstt)方法。ppp方法，传统上使用消电离层组合的方法，需要双频数据，而由于单频接收机成本低廉，在当前卫星导航定位，时间传递领域拥有大量用户，因此，使用廉价的单频接收机，去实现高精度单机时间频率传递，恰好能满足低成本高精度单机用户的要求。在复杂多变的外部环境无法保证双频数据的准确性和连续性的条件下，单频算法能够使双频接收机维持使用。而保证时间传递的连续性与准确性是时间频率传递在实际应用中的急需解决的瓶颈问题。开展基于多gnss单频伪距与载波相位观测值的精密单点定位算法用于时间频率传递领域的研究，将显著提升基于导航卫星的高精度时间频率传递的性能与鲁棒性，可更好地服务于国防与民生等应用领域。

技术实现要素：

为克服现有技术的不足，本发明提供一种基于多gnss的单频伪距载波相位观测值的两地时间频率传递模型，该模型能够实现将多gnss精密单点定位算法应用于高精度的时间频率传递，可保证高精度时间频率传递的鲁棒性和连续性。

本发明基于多gnss的单频精密单点定位算法的时间频率传递方法，包括下列步骤：

步骤1：第一接收机a接有高精度的第一外接原子钟a，第一外接原子钟a为第一接收机a提供1pps/10m的高精度时间频率信号；

步骤2：第一接收机a通过天线接收到多个卫星系统的单频点伪距、载波相位观测数据，将二者统称为第一单频观测数据；

步骤3：基于第一单频观测数据与精密产品数据，进行钟差参数估计，解算得到本地的第一钟差参数clocka-参考时间，也就是本地的第一接收机a的时钟与使用的精密产品参考时间尺度的差值；

步骤4：第二接收机b接有高精度的第二外接原子钟b，第二外接原子钟b为第二接收机b提供1pps/10m的高精度时间频率信号；

步骤5：第二外接接收机b通过天线接收到多个卫星系统的单频点伪距、载波相位观测数据，将二者统称为第二单频观测数据；

步骤6：基于第二单频观测数据与精密产品数据，进行钟差参数估计，解算得到本地的第二钟差参数clockb-参考时间，也就是本地的第二接收机b的时钟与使用的精密产品参考时间尺度的差值；

步骤7：对两地得到的第一钟差参数clocka、第二钟差参数clockb进行统一，同时对两地的接收机进行仪器测量的方式或者使用接收机给出的标校值，进而完成两地的时间频率传递，得到相应的应用；

clocka-clockb＝(clocka-参考时间)-(clockb-参考时间)。

在本发明的一个实施例中，钟差参数估计具体包括下列步骤：

步骤1：首先从外接有高精度原子钟的gnss接收机获取到单频点伪距、载波相位观测数据；

步骤2：根据是否需要电离层产品选择具体的处理策略，如果选择需要电离层产品，那么根据实际精度的要求，从外部获取电离层产品；

步骤3：如果不需要获取电离层产品，或者需要获取，在获取电离层产品成功后，同时获取相应时间的精密轨道、精密钟差、差分码偏差dcb产品；

步骤4：上述所有数据准备好后，开始逐一历元进行处理，将上述数据代入以下载波相位与伪距观测方程中，如果有电离层产品，将电离层产品作为已知参数代入；

以下方程为基础，通过模型修正、外部产品以及参数估计手段，对与卫星有关的误差，包括卫星钟差、卫星轨道误差、相对论效应、与接收机和测站有关的误差，包括接收机钟差、接收机天线相位误差、地球潮汐、地球自转、与信号传播有关的误差，包括对流层延迟误差、电离层延迟误差和多路径效应，进行处理；

其中，p与φ分别代表伪距与载波相位观测值，所有的上角标s代表卫星号，所有的下角标r代表接收机，所有的下角标j代表频点；所以与分别代表j频点数据，在卫星s与接收机r之间的伪距与载波相位观测值；

代表接收机r与卫星s的站星几何距离，c代表光速，dtr代表接收机钟差，dt^s代表卫星s的钟差，zw代表湿的天顶方向对流层延迟，w代表“湿”，mfw(e)代表投影函数，本公式中代表j频点的基于1频点的电离层延迟系数，代表第一频点卫星s到接收机的电离层延迟，与分别代表j频点伪距在卫星与接收机端的硬件延迟，与分别代表j频点载波相位在卫星与接收机端的硬件延迟，代表j频点信号，卫星s到r接收机的模糊度参数，与分别代表j频点信号，卫星s到r接收机伪距观测值p与载波相位观测值φ的残差，也即函数模型对所有误差没有量化的部分；

步骤5：如果电离层参数未知，无法从外部获取已知的电离层值使用半和模型进行消电离层参数，由公式6推导得到如下公式：

其中，这里的l对应公式(1)的φ，代表j频点数据，在卫星s与接收机r之间的载波相位观测值，为线性化方程得到的参数，而由于使用的是基于p1/p2码得到的卫星钟差产品，所以代表的是对于差分码偏差进行修正项，其中为dcb修正系数，使用不同的频点以及码组合将需要不同的修正系数，代表基于p1/p2码的差分码偏差产品；x代表线性化待估参数，其中包含钟差参数；代表消电离层组合的卫星钟差产品；的方程为整合得到的函数观测方程；为整合得到的延迟参数,为待估计参数；

通过半和模型，对电离层参数进行消除，除了电离层的处理，再获取相应的精密轨道、精密钟差、dcb的产品代入公式7；

步骤6：对准备好单个历元数据，进行基本的质量控制，包括对粗差的剔除、周跳的探测；

步骤7：进行扩展卡尔曼滤波处理，对钟差参数dtr进行估计，得到相应的观测数据残差估计参数公式如下所示：

时间更新方程：

其中，其中n维向量为k时刻的系统状态变量，n维向量是k-1时刻的系统状态变量；a是状态转移矩阵或者过程增益矩阵，是n×n阶方阵，其上标t为“转置”，它将k-1时刻状态和当前的k时刻状态联系起来；b是可选的控制输入的增益，uk-1为驱动噪声，在大多数实际情况下并没有控制增益，所以buk-1这一项为零；为x参数的协方差矩阵，q为状态方程噪声；

状态更新方程：

其中kk表示卡尔曼增益，是滤波的中间结果，h表示量测矩阵，是m×n阶矩阵，它把m维测量值转换到n维与状态变量相对应；zk表示测量值，是m阶向量；r为观测噪声矩阵，为更新的待估计参数，pk为更新的待估计参数协方差矩阵；

步骤8：对应卫星残差过大，则剔除该卫星，回到步骤7进行重新估计，直到所有数据满足阈值条件为止；阈值的使用根据实际处理过程经验值；

步骤9：保存相关结果钟差参数dtr，估计的同时，得到坐标、模糊度、系统间偏差参数，保存该历元结果的同时，回到步骤6，进行下一个历元结果的处理。

本发明的有益效果是：

第一，可以对多gnss与单频伪距与载波相位用于高精度时间频率传递数据处理模型进行统一。本发明将多gnss和单频两种数据处理模型进行有机统一，在复杂多变的外部环境和需求情况下，无法实现双频解算时，可更好地实现基于gnss单频数据获得高度鲁棒性与稳定性。基于统一的数据处理模型，可实现多系统和单频两种算法的有机统一。

第二，为高精度时间频率传递用户提供选择多样性。对于电离层的处理，实现多种模式切换，以适应复杂多变的环境，更好地适应用户需求。

附图说明

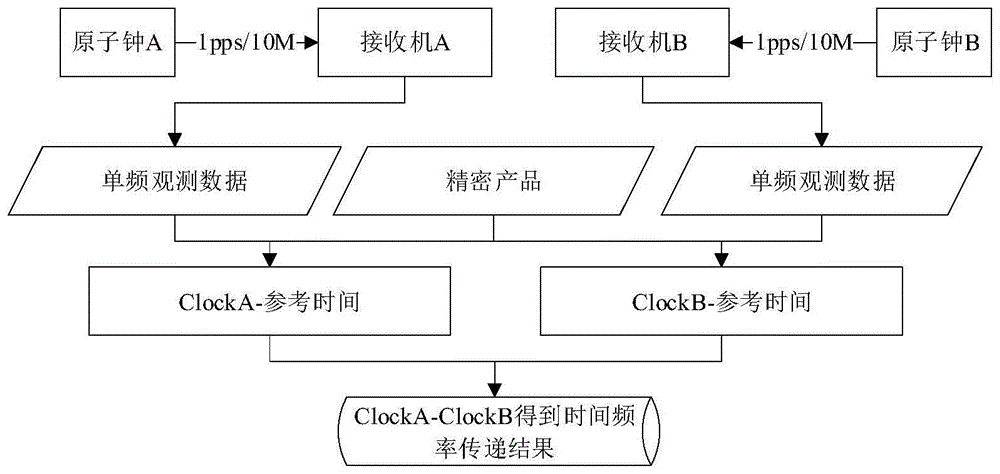
图1是基于导航卫星的高精度时间频率传递方法实施框图；

图2是基于gnss单频伪距与载波相位的钟差解算方法流程图。

具体实施方式

下面结合附图和实施例对本发明进一步说明，本发明包括但不仅限于下述实施例。

本发明将多gnss和单频高精度时间频率传递方法进行有机融合，建立高鲁棒性的统一模型，用户可以获取高精度时间频率的稳定性和连续性。本发明可将北斗卫星导航系统(bds)应用于时间频率行业，更好地服务于国防、军事、电力、通信、银行、金融等行业。

本发明的技术方案主要包括三个核心技术：

(1)各项误差的处理

通过模型修正、外部产品以及参数估计等手段，对与卫星有关的误差(卫星钟差、卫星轨道误差、相对论效应)、与接收机和测站有关的误差(接收机钟差、接收机天线相位误差、地球潮汐、地球自转等)、与信号传播有关的误差(对流层延迟误差、电离层延迟误差和多路径效应)进行处理。这些处理均为本领域技术人员熟知，不再累述。

(2)单频点电离层误差的处理

第1种方法是采用电离层模型改正(参见各个卫星导航系统的导航文件icd接口文件)，不同系统的广播星历里面包含不同的电离层参数模型；第2种方法是根据电离层引起的群延迟和相延迟大小相等、方向相反这一特点，采用码和相位的半合组合进行修正(参见高扬论文gaoy,shenx.anewmethodforcarrier-phase-basedprecisepointpositioning[j].navigation,2002,49(2):p.109-116)；第3种方法是将电离层延迟当作未知参数，类似与本专利要估计的钟差参数同时进行估计。

(3)建立函数模型进行钟差参数估计

根据选择的电离层处理方式不一样，建立不同的函数模型，以下对具体涉及的函数模型进行解释。首先对于接收机观测到的伪距与载波相位可以直接给出伪距与载波相位观测方程，如下所示：

其中，p与φ分别代表伪距与载波相位观测值，所有的上角标s代表卫星号，所有的下角标r代表接收机，所有的下角标j代表频点。所以与分别代表j频点数据，在卫星s与接收机r之间的伪距与载波相位观测值。

代表接收机r与卫星s的站星几何距离，c代表光速，dtr代表接收机钟差，dt^s代表卫星s的钟差，zw代表湿的天顶方向对流层延迟，w代表湿(wet)的意思，mfw(e)代表投影函数，代表j频点的基于1频点的电离层延迟系数，代表第一频点卫星s到接收机的电离层延迟，与分别代表j频点伪距在卫星与接收机端的硬件延迟，与分别代表j频点载波相位在卫星与接收机端的硬件延迟，代表j频点信号，卫星s到r接收机的模糊度参数，与分别代表j频点信号，卫星s到r接收机伪距观测值p与载波相位观测值φ的残差，也即函数模型(公式)对所有误差没有量化的部分。

由于选择单频数据，这里只以gnss的第一频点数据为例，由于卡尔曼滤波只能是对线性方程进行，所以对上两式进行线性化处理得到：

其中，这里的l对应上面公式(1)的φ，代表j频点数据，在卫星s与接收机r之间的载波相位观测值，为线性化方程得到的参数，而由于我们使用的是基于p1/p2码得到的卫星钟差产品，所以这里代表的是对于差分码偏差进行修正项，其中为dcb修正系数，使用不同的频点以及码组合将需要不同的修正系数，代表基于p1/p2码的差分码偏差产品。x代表线性化待估参数，其中包含钟差参数。代表消电离层组合的卫星钟差产品。

如果没有电离层产品，对电离层使用半和模型，半和模型为基于伪距观测值与载波相位观测值在穿越电离层时延迟大小相等，符号相反特性进行整合，整合上述两个公式得到如下所示：

其中，的方程为整合得到的函数观测方程。为整合得到的延迟参数,为待估计参数。

如果是多系统(bds,gps,galileo,glonass,qzss)，则多估计一个isb(系统间偏差)参数，得到待估参数，有电离层估计与无电离层估计参数序列分别为：

x1＝[x,dtr,isb,zw，i,nb,ns](4)

x2＝[x,dtr,isb,zw,nb,ns](5)

其中，x代表待估计位置参数，dtr代表待估计参数接收机钟差，isb为多系统条件下系统参数，zw为湿的天顶对流层延迟，i为电离层延迟，其中b与s分别代表基准系统与增加的系统，nb为基准系统模糊度，ns为增加的系统模糊度。

最后，根据(2)或(3)公式，利用扩展卡尔曼滤波估算得到本地钟差数据dtr，同时对两地的接收机硬件延迟进行标校，进而完成对两地的钟差进行统一与比对，实现高精度的时间频率传递。这个过程可以是事后，也可以是实时模式，取决于用户的具体需求。

图1描述本发明基于多gnss的单频精密单点定位算法的时间频率传递方法的总体实施方案流程，具体如下：

步骤1：接收机a接有高精度的外接原子钟a，原子钟a为接收机a提供1pps/10m的高精度时间频率信号。

步骤2：接收机a通过天线接收到多个卫星系统的单频点伪距，载波相位观测数据。

步骤3：基于单频观测数据与精密产品数据，进行钟差参数估计，详细处理方法如图2所示，精密产品为例如来源于欧洲定轨中心code、德国地学研究中心gfz等的精密轨道、精密钟差(本领域技术人员熟知)，解算得到本地的钟差参数clocka-参考时间，也就是本地的接收机钟与使用的精密产品参考时间尺度的差值。

步骤4：接收机b接有高精度的外接原子钟b，原子钟b为接收机b提供1pps/10m的高精度时间频率信号。

步骤5：接收机b通过天线接收到多个卫星系统的单频点伪距，载波相位观测数据。

步骤6：基于单频观测数据与精密产品数据，进行钟差参数估计，详细处理方法如图2所示，单频观测数据与精密产品，解算得到本地的钟差参数clockb-参考时间，也就是本地的接收机钟b与使用的精密产品参考时间尺度的差值。

步骤7：对两地得到的钟差参数(clocka,clockb)进行统一，同时对两地的接收机进行仪器测量的方式或者使用接收机给出的标校值，进而完成两地的时间频率传递，得到相应的应用。

clocka-clockb＝(clocka-参考时间)-(clockb-参考时间)

图2描述图1中子流程，描述了其中钟差参数估计的详细算法步骤。

步骤1：首先从gnss接收机(外接有高精度原子钟)获取到单频点的伪距，载波相位数据。

步骤2：根据是否需要电离层产品选择具体的处理策略，如果选择需要电离层产品，那么从外部获取，根据实际精度的要求，有很多种方式。例如国际上code等机构获取ion产品精度较高，也可以从广播星历中提取参数进行模型改正，精度较低。

步骤3：如果不需要获取电离层产品，或者需要获取，获取电离层产品成功后，同时获取相应时的精密轨道，精密钟差，差分码偏差(dcb)等产品，如果上述过程是实时模式，就实时获取，如果是事后模式，可采用事后下载方式获取。

步骤4：将所有数据准备好以后，开始逐一历元进行处理，例如1:00:00估计一次，1:00:05估计一次，每隔5秒估计一次，逐一历元进行估计，实际估计间隔根据观测数据的采样间隔。可以代入以下载波相位与伪距观测方程中，如果有电离层产品，将电离层产品作为已知参数代入。

以下方程为基础，通过模型修正、外部产品以及参数估计等手段，对与卫星有关的误差(卫星钟差、卫星轨道误差、相对论效应)、与接收机和测站有关的误差(接收机钟差、接收机天线相位误差、地球潮汐、地球自转等)、与信号传播有关的误差(对流层延迟误差、电离层延迟误差和多路径效应)进行处理。这些处理均为本领域技术人员熟知，不再累述。

步骤5：如果电离层参数未知，无法从外部获取已知的电离层值可以使用半和模型(参见高扬论文gaoy,shenx.anewmethodforcarrier-phase-basedprecisepointpositioning[j].navigation,2002,49(2):p.109-116)进行消电离层参数，由公式6推导得到如下公式：

通过半和模型，对电离层参数进行了消除，除了电离层的处理，再获取相应的精密轨道，精密钟差，dcb等产品代入公式7。此时所有公式中已知数据准备好，可以进下一步。

步骤6：对准备好单个历元数据，进行基本的质量控制，包括对粗差的剔除，周跳的探测等等。该步骤的具体实施方法为本领域技术人员熟知，不再累述。

步骤7：进行扩展卡尔曼滤波处理，对钟差参数dtr进行估计，得到相应的观测数据残差估计参数公式如下所示：

时间更新方程：

其中，其中n维向量为k时刻的系统状态变量，n维向量是k-1时刻的系统状态变量。a是状态转移矩阵或者过程增益矩阵，是n×n阶方阵，其上标t为“转置”，它将k-1时刻状态和当前的k时刻状态联系起来。b是可选的控制输入的增益，uk-1为驱动噪声，在大多数实际情况下并没有控制增益，所以buk-1这一项为零。为x参数的协方差矩阵，q为状态方程噪声。

状态更新方程：

其中kk表示卡尔曼增益，是滤波的中间结果，h表示量测矩阵，是m×n阶矩阵，它把m维测量值转换到n维与状态变量相对应。zk表示测量值，是m阶向量。r为观测噪声矩阵，为更新的待估计参数，pk为更新的待估计参数协方差矩阵。

步骤8：对应卫星残差过大，则剔除该卫星，回到步骤7进行重新估计，直到所有数据满足阈值条件为止。阈值的使用根据实际处理过程经验值。

步骤9，保存相关结果钟差参数dtr，估计的同时，我们会得到坐标，模糊度，系统间偏差等参数，在此专利中我们不予使用，保存该历元结果的同时，我们回到步骤6，进行下一个历元结果的处理。

自全球卫星导航系统(gnss)问世以来,由于其具有全球性、全天候、高精度、高效率、保密性强等一系列特点,现已被广泛应用于卫星导航、测量定位、形变监测、大气探测，高精度时间频率传递等领域。目前,gnss精密导航与定位与授时，一般都采用双频接收机,其主要原因是为了消除电离层误差的影响。在利用gnss技术开展区域变形监测、大气探测、时间频率传递、时间同步等研究中,由于需要采集高时空分辨率的信息,不得不布设大量的gnss接收机。如全部采用gnss双频接收机进行施测,其成本无疑将非常昂贵,这必然会极大限制gnss技术在这些领域未来的发展和应用。正因为如此,如何消除电离层误差的影响,利用相对廉价的单频接收机实现大范围的高精度时间频率传递测试与使用，正是本发明解决的问题。现有技术尚未出现使用过单频方法进行时间传递的解决方案，本发明针对单频解决方案，在有无外部辅助电离层产品的情况下，提出对应解决方案。