多孔介质孔径分布表征方法及电子设备与流程

1.本发明属于多孔介质表征领域，具体涉及一种多孔介质孔径分布表征方法及电子设备。


背景技术：

2.多孔介质的孔隙结构特征对药物释放、催化剂效能、滤材过滤效果、建材性能、岩石储集能力等均有重要影响，孔径分布是孔隙结构研究中的重要内容。以孔隙大小(直径/半径等)为横坐标，孔隙体积或体积对大小的微分为纵坐标的孔径分布曲线是研究孔隙结构特征的关键图件。在石油地质领域，致密油气、页岩油气等非常规油气的勘探开发已经成为油气增储上产的关键领域。低孔低渗的致密砂岩、灰岩、泥页岩等储层孔隙是非常规油气赋存的场所，其孔径分布特征深刻影响着油气的赋存状态、流动能力、产出特征等，是目前和未来研究的热点。为了揭示泥页岩等致密储层孔隙结构特征，国内外不同学者根据高压压汞、氮气吸附等实验数据制作孔径分布曲线，用来描述峰值分布、不同尺度孔隙多少等特征。
3.孔径分布曲线横坐标为孔隙的半径或直径，纵坐标类型主要有两类：一是孔体积增量，单位为ml/g、％等，含义为单位质量样品一定孔径区间内的孔体积或占比；二是孔体积变化率，单位为ml/(g
·
nm)等，含义为孔体积随孔径的变化率，其曲线与横坐标围成的面积可代表孔体积。
4.在国内外文献中，时常可见到第一类孔径分布曲线。比如：朱炎铭(2016)等用压汞数据，以孔径(nm)的对数为横坐标，阶段进汞量为纵坐标(ml/g)制作了泥页岩孔径分布曲线；张大智等(2017)利用氮气吸附数据，以孔径(nm)的对数为横坐标，以孔体积(cm3/g)为纵坐标制作了致密砂岩的孔径分布曲线；孟子圆等(2019)用压汞数据，以孔喉半径(μm)的对数为横坐标，以进汞饱和度为纵坐标制作了致密砂岩孔径分布曲线；lubelli b等(2013)用高压压汞数据，以孔隙直径(μm)为横坐标，以体积增加量(％)为纵坐标制作了膨润土孔径分布曲线；zhixiong zeng等(2020)利用氮气吸附数据，以孔隙直径(nm)为横坐标，以孔体积增量(cm3/g)为纵坐标制作了孔径分布曲线。
5.在上述第一类孔径分区曲线的制作过程中，很多学者往往对实验报告数据直接应用，报告数据点分布的不均匀性会对孔径分布曲线形态产生显著影响，进而影响对孔径分布特征的判断。以2017年《天然气地球科学》28卷第6期903页的一张图来具体说明，如图1所示。该图纵坐标为孔体积，单位是cm3/g，横坐标是孔径的对数形式，根据图中曲线高峰个数，将样品划分为双峰型和三峰型。文中指出双峰型存在在一个主峰(30-60nm)、一个次峰(7-10nm)；三峰型孔径分布曲线存在1个主峰(30-60nm)、2个次峰(7-10nm、100-110nm)。习惯上认为，峰值越高，与x轴围城的面积越大，该范围内孔隙越发育，那么图中展示的10nm以下微孔曲线最接近x轴，视觉上其面积较小，应该具有较小的孔隙体积。但实际上，10nm以下的孔体积占比达到25％以上，这与图中展示的视觉效果差别较大。原因就在于忽略了这类孔径分布曲线的含义，纵坐标的含义是单位样品中的孔隙体积，该曲线与x轴围成的面积并
非是孔隙体积，某点的含义是该点前一点的孔径到该点的孔径区间内增加的孔隙体积。同时，该曲线坐标点的横坐标分布不均匀，小孔隙坐标点间隔小，大孔隙坐标点间隔大，这就导致了峰值的不真实性。也就是说，坐标点的疏密对峰值的大小分布产生重要影响，若《10nm孔隙范围内的坐标点仅有3个，那么可以预见的是《10nm会出现明显的高峰。所以，以孔体积增量(单位为mg/l、％等)为纵坐标，以孔径(坐标为nm、μm等)为横坐标的孔径分布曲线，若坐标点的选取未能按照等距离原则，将会对孔径分布曲线形态产生重要影响，误导孔隙结构特征的分析。
6.专利“页岩全孔径孔隙体积的表征方法”(申请号cn201510785013.9)包括如下步骤：1)分别对柱状页岩、第一粉状页岩和第二粉状页岩依次进行脱水和脱气处理；2)采用高压压汞法对柱状页岩进行分析，结合washburn方程得到第一孔径范围内各孔径的孔隙体积；3)采用氮气吸附法对第一粉状页岩进行分析，结合bjh模型得到第二孔径范围内各孔径的孔隙体积；4)采用二氧化碳吸附法对第二粉状页岩进行分析，结合dft模型得到第三孔径范围内各孔径的孔隙体积；5)如第一孔径范围、第二孔径范围和第三孔径范围之间重叠范，采用加权平均法得到重叠范围内各孔径的孔隙体积，该方法解决了不同测试方法重叠区间的取值问题。
7.专利“基于模拟压汞法获取岩石的孔径分布的方法和装置”(申请号cn201810227776.5)主要包括以下步骤：获取待测定岩石的岩心的至少部分的三维数字图像，根据该三维数字图像，获取岩心的至少部分包括的孔隙的骨架图像，获取该骨架图像包括的所有点各自对应的孔径值，点对应的孔径值为点距离孔隙边界的最小距离的两倍，根据骨架图像包括的各点各自对应的孔径值，通过模拟压汞法获取待测定岩石的孔隙的孔径分布。该专利申请的方法，可测定的孔隙尺寸的范围不受限制，可获取各种待测定岩石的孔隙的孔径分布。该专利的附图9的孔径分布区曲线以是以孔径对数为横坐标，以孔体积为纵坐标，可明显看出小孔数据点更密，大孔数据点相对稀疏。
8.专利“一种致密油/页岩油的纳米级含油孔径分布的测定方法”(申请号cn201710012951.4)包括如下步骤：致密砂岩样品或页岩样品经粉碎后得到粉末样品，部分粉末样品进行有机溶剂抽提得抽提后样品，部分粉末样品作为抽提前样品；将抽提前样品和抽提后样品分别进行孔径分布测试得抽提前样品和抽提后样品的孔径分布曲线；对两条曲线分别进行拟合得抽提前样品和抽提后样品的微孔-介孔-宏孔的孔径分布，抽提后样品的比孔容与抽提前样品的比孔容之间的差值即为含油孔隙空间的比孔容，至此即得到致密油或页岩油的纳米级含油孔径分布。
9.综上，现有技术主要以测试装置/方法改进、不同方法重叠区间处理、孔隙内含物的确定等为主要内容，存在多孔介质孔径分布测试数据点不均匀分布，孔径分布曲线不能直观反映孔径分布特征的问题。
10.因此，特别需要一种使得多孔介质孔径分布测试数据点均匀分布，能直观反映孔径分布特征的多孔介质孔径分布表征方法。


技术实现要素：

11.本发明的目的是提出一种使得多孔介质孔径分布测试数据点均匀分布，能直观反映孔径分布特征的多孔介质孔径分布表征方法。
12.有鉴于此，本发明提供了一种多孔介质孔径分布表征方法及电子设备至少解决现有技术中不能直观反映多孔介质孔径分布特征的问题。
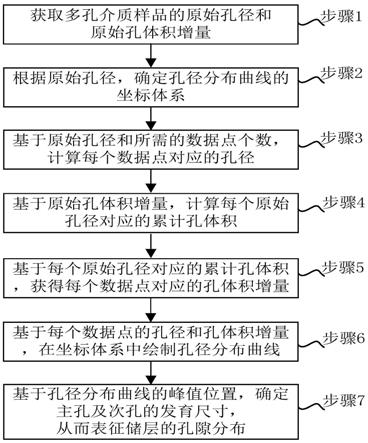
13.第一方面，本发明提供一种多孔介质孔径分布表征方法，包括：获取多孔介质样品的原始孔径和原始孔体积增量；根据所述原始孔径，确定孔径分布曲线的坐标体系；基于所述原始孔径和所需的数据点个数，计算每个数据点对应的孔径；基于所述原始孔体积增量，计算每个原始孔径对应的累计孔体积；基于每个所述原始孔径对应的累计孔体积，获得每个数据点对应的孔体积增量；基于所述每个数据点的孔径和孔体积增量，在所述坐标体系中绘制孔径分布曲线；基于所述孔径分布曲线的峰值位置，确定主孔及次孔的发育尺寸，从而表征储层的孔隙分布。
14.可选的，通过高压压汞、氮气吸附、co2吸附或核磁共振对所述多孔介质样品进行孔径分布测试实验，获得多孔介质样品的原始孔径和原始孔体积增量；所述原始孔体积增量指所述每个原始孔径区间内的孔体积。
15.可选的，所述根据所述原始孔径，确定孔径分布曲线的坐标体系包括：计算所述原始孔径的最大值与最小值的商；若所述最大值与最小值的商大于预设阈值，则所述坐标体系为对数坐标系，横坐标为孔径的对数，纵坐标为孔体积增量；若所述最大值与最小值的商小于预设阈值，则所述坐标体系为普通坐标系，横坐标为孔径，纵坐标为孔体积增量。
16.可选的，所述基于所述原始孔径和所需的数据点个数，计算每个数据点对应的孔径包括：基于所述原始孔径和所需的数据点个数，计算坐标间隔；基于所述坐标间隔和原始孔径，计算每个数据点对应的孔径。
17.可选的，当所述坐标体系的横坐标为普通坐标系时，采用下述公式计算坐标间隔：
18.d
int
＝(d
max-d
min
)/(n-1)
19.其中，d
int
为坐标间隔；d
max
为原始孔径的最大值；d
min
为原始孔径的最小值；n为数据点个数；
20.当所述坐标体系的横坐标为对数坐标系时，采用下述公式计算坐标间隔：
21.logm(d
int
)＝(logm(d
max
)-logm(d
min
))/(n-1)
22.其中logm(d
int
)为坐标间隔对数值；logm(d
max
)为原始孔径的最大值对数；logm(d
max
)为原始孔径的最小值对数，m为基数。
23.可选的，当所述坐标体系的横坐标为普通坐标系时，采用下述公式计算每个数据点对应的孔径：
24.di＝d
min
+d
int
×
(i-1)
25.当所述坐标体系的横坐标为对数坐标系时，采用下述公式计算每个数据点对应的孔径：
26.logm(di)＝logm(d
min
)+logm(d
int
)
×
(i-1)
27.di＝(logm(di))m28.其中，di为第i个数据点的孔径。
29.可选的，所述每个原始孔径对应的累计孔体积为小于或等于所述原始孔径的孔体积增量之和，即
[0030][0031]
其中，v
cn
为第n个原始孔径对应的累计孔体积，vj为第j个原始孔径的孔体积增量，
n为小于或等于第n个原始孔径的原始孔径总个数。
[0032]
可选的，所述基于每个所述原始孔径对应的累计孔体积，获得每个数据点的孔体积增量包括：对每个所述原始孔径对应的累计孔体积进行插值，获得每个数据点的累计孔体积；基于所述每个数据点的累计孔体积，计算每个数据点的孔体积增量。
[0033]
可选的，采用下述公式计算每个数据点对应的孔体积增量：
[0034]vi
＝v
ci-v
c(i-1)
[0035]
其中，vi为第i个数据点对应的孔体积增量，v
ci
为第i个数据点对应的累积孔体积，v
ci-1
第i-1个数据点对应的累积孔体积。
[0036]
第二方面，本发明还提供一种电子设备，所述电子设备包括：存储器，存储有可执行指令；处理器，所述处理器运行所述存储器中的所述可执行指令，以实现上述多孔介质孔径分布表征方法。
[0037]
本发明的有益效果在于：本发明的多孔介质孔径分布表征方法能够表征实际孔体积的相对大小，解决了多孔介质孔径分布测试数据点不均匀分布的问题，可根据峰值位置确定主孔及次孔的发育尺寸，反应储层的孔隙分布特征，有利于评价储层的好坏，为储层的开发提供依据。
[0038]
本发明具有其它的特性和优点，这些特性和优点从并入本文中的附图和随后的具体实施例中将是显而易见的，或者将在并入本文中的附图和随后的具体实施例中进行详细陈述，这些附图和具体实施例共同用于解释本发明的特定原理。
附图说明
[0039]
通过结合附图对本发明示例性实施方式进行更详细的描述，本发明的上述以及其它目的、特征和优势将变得更加明显，其中，在本发明示例性实施方式中，相同的参考标号通常代表相同部件。
[0040]
图1示出了现有技术的孔径分布曲线图。
[0041]
图2示出了根据本发明的一个实施例的一种多孔介质孔径分布表征方法的流程图。
[0042]
图3示出了根据本发明的一个实施例的一种多孔介质孔径分布表征方法的基于氮气吸附数据的普通坐标孔径分布曲线图。
[0043]
图4示出了根据本发明的一个实施例的一种多孔介质孔径分布表征方法的基于高压压汞数据的对数坐标孔径分布曲线图。
具体实施方式
[0044]
下面将更详细地描述本发明的优选实施方式。虽然以下描述了本发明的优选实施方式，然而应该理解，可以以各种形式实现本发明而不应被这里阐述的实施方式所限制。
[0045]
本发明提供本发明提供一种多孔介质孔径分布表征方法，包括：获取多孔介质样品的原始孔径和原始孔体积增量；根据原始孔径，确定孔径分布曲线的坐标体系；基于原始孔径和所需的数据点个数，计算每个数据点对应的孔径；基于原始孔体积增量，计算每个原始孔径对应的累计孔体积；基于每个原始孔径对应的累计孔体积，获得每个数据点对应的孔体积增量；基于每个数据点的孔径和孔体积增量，在坐标体系中绘制孔径分布曲线；基于
孔径分布曲线的峰值位置，确定主孔及次孔的发育尺寸，从而表征储层的孔隙分布。
[0046]
具体的，根据多孔介质样品的原始孔径，选取合适坐标体系及确定坐标间隔，根据坐标间隔计算目标数据点孔径；根据多孔介质样品的原始孔体积增量计算原始孔径对应的累积孔体积，对原始孔径对应的累积孔体积进行插值计算目标数据点孔径对应的孔体积增量，以选取的坐标体系的孔径或孔径的对数为横坐标，以数据点的孔体积增量为纵坐标，生成孔径分布曲线，根据孔径分布曲线的峰值位置确定主孔及次孔的发育尺寸，进而反应储层的空隙分布特征。
[0047]
本技术生成的孔径分布曲线与横轴围成面积的相对大小能代表实际孔体积的相对大小，峰值分布更符合实际，解决了多孔介质孔径分布测试数据点不均匀分布，解决了孔径分布曲线不能直观反映孔径分布特征的技术问题。
[0048]
根据示例性的实施方式，多孔介质孔径分布表征方法能够表征实际孔体积的相对大小，解决了多孔介质孔径分布测试数据点不均匀分布的问题，可根据峰值位置确定主孔的发育尺寸，反应储层的孔隙分布特征，有利于评价储层的好坏，为储层的开发提供依据。
[0049]
作为可选方案，通过高压压汞、氮气吸附、co2吸附或核磁共振对多孔介质样品进行孔径分布测试实验，获得多孔介质样品的原始孔径和原始孔体积增量；所述原始孔体积增量指所述每个原始孔径区间内的孔体积。
[0050]
具体的，对多孔介质样品进行孔径分布测试实验，获得样品孔径分布测试数据，实验可以是高压压汞、氮气吸附、co2吸附、核磁共振等一种或多种。通过各测试方法对应的数学模型，原始实验测试数据可被处理成包括孔径、孔体积增量(孔体积占比或累计孔体积)两项信息的数据。
[0051]
作为可选方案，根据原始孔径，确定孔径分布曲线的坐标体系包括：计算原始孔径的最大值与最小值的商；若最大值与最小值的商大于预设阈值，则坐标体系为对数坐标系，横坐标为孔径的对数，纵坐标为孔体积增量；若最大值与最小值的商小于预设阈值，则坐标体系为普通坐标系，横坐标为孔径，纵坐标为孔体积增量。
[0052]
具体的，根据测试数据，结合研究需要，选取合适的坐标体系。一般的，若需要作图的数据点最大孔径是最小孔径的1000倍以上，横坐标应选取基m大于1的对数坐标，若最大最小横坐标之比低于1000，选取普通横坐标即可。
[0053]
作为可选方案，基于原始孔径和所需的数据点个数，计算每个数据点对应的孔径包括：基于原始孔径和所需的数据点个数，计算坐标间隔；基于坐标间隔和原始孔径，计算每个数据点对应的孔径。
[0054]
作为可选方案，当坐标体系的横坐标为普通坐标系时，采用下述公式计算坐标间隔：
[0055]dint
＝(d
max-d
min
)/(n-1)
[0056]
其中，d
int
为坐标间隔；d
max
为原始孔径的最大值；d
min
为原始孔径的最小值；n为数据点个数；
[0057]
当坐标体系的横坐标为对数坐标系时，采用下述公式计算坐标间隔：
[0058]
logm(d
int
)＝(logm(d
max
)-logm(d
min
))/(n-1)
[0059]
其中logm(d
int
)为坐标间隔对数值；logm(d
max
)为原始孔径的最大值对数；logm(d
max
)为原始孔径的最小值对数，m为基数。
[0060]
根据研究需要，确定孔径分布曲线的数据点个数n，n可以与原始报告中数据点个数相同，也可以大于或小于原始报告数据点数。若选取的横坐标为普通坐标，则利用下述公式计算坐标间隔：
[0061]dint
＝(d
max-d
min
)/(n-1)；
[0062]
若选取的横坐标为对数坐标，则利用下述公式计算坐标间隔的对数值：
[0063]
logm(d
int
)＝(logm(d
max
)-logm(d
min
))/(n-1)
[0064]
其中：d
int
为坐标间隔；d
max
最大原始孔径值；d
min
为最小原始孔径值；n为数据点个数；m为对数的基；logm(d
int
)为坐标间隔对数值；logm(d
max
)为最大原始孔径对数；logm(d
max
)为最小原始孔径对数。
[0065]
作为可选方案，当坐标体系的横坐标为普通坐标系时，采用下述公式计算每个数据点对应的孔径：
[0066]di
＝d
min
+d
int
×
(i-1)
[0067]
当坐标体系的横坐标为对数坐标系时，采用下述公式计算每个数据点对应的孔径：
[0068]
logm(di)＝logm(d
min
)+logm(d
int
)
×
(i-1)
[0069]di
＝(logm(di))m[0070]
其中，di为第i个数据点的孔径。
[0071]
若选取的横坐标为普通坐标，则利用下述公式计算目标数据点孔径；
[0072]di
＝d
min
+d
int
×
(i-1)；
[0073]
若选取的横坐标为对数坐标，则利用下述公式计算目标数据点孔径；
[0074]
logm(di)＝logm(d
min
)+logm(d
int
)
×
(i-1)；
[0075]di
＝(logm(di))m。
[0076]
作为可选方案，每个原始孔径对应的累计孔体积为小于或等于原始孔径的孔体积增量之和，即
[0077][0078]
其中，v
cn
为第n个原始孔径对应的累计孔体积，vj为第j个原始孔径的孔体积增量，n为小于或等于第n个原始孔径的原始孔径总个数。
[0079]
具体的，根据原始数据计算不同孔径d对应的累积孔隙体积vc，某孔径d对应的累积孔隙体积vc是小于等于该孔径的孔体积增量vi之和如下述公式，累积孔隙体积vc随孔径d增大而增大。
[0080][0081]
作为可选方案，基于每个原始孔径对应的累计孔体积，获得每个数据点的孔体积增量包括：对每个原始孔径对应的累计孔体积进行插值，获得每个数据点的累计孔体积；基于每个数据点的累计孔体积，计算每个数据点的孔体积增量。
[0082]
具体的，目标数据点横坐标一般无法与原始数据中的孔径对应，按照以下2步确定不同孔径对应的孔体积增量。
[0083]
(1)对原始孔径的累计孔体积进行插值，得到不同孔径对应累积孔体积。
[0084]
作为可选方案，采用下述公式计算每个数据点对应的孔体积增量：
[0085]vi
＝v
ci-v
c(i-1)
[0086]
其中，vi为第i个数据点对应的孔体积增量，v
ci
为第i个数据点对应的累积孔体积，v
ci-1
第i-1个数据点对应的累积孔体积。
[0087]
插值模型可选取线性插值模型，该模型利用小于孔径的原始孔径中最大值d
imax
和大于孔径的原始孔径中最小值d
imin
对应得累积孔体积v
cimax
和v
cimin
进行线性计算，如下公式：
[0088][0089]
当然，插值模型也可根据需要，选取抛物插值、二次插值、样条插值等。
[0090]
利用累积孔体积计算不同孔径对应的孔体积增量，如下公式：
[0091]vi
＝v
ci-v
c(i-1)
。
[0092]
本发明还提供一种电子设备，电子设备包括：存储器，存储有可执行指令；处理器，处理器运行存储器中的可执行指令，以实现上述多孔介质孔径分布表征方法。
[0093]
实施例一
[0094]
图2示出了根据本发明的一个实施例的一种多孔介质孔径分布表征方法的流程图。图3示出了根据本发明的一个实施例的一种多孔介质孔径分布表征方法的基于氮气吸附数据的普通坐标孔径分布曲线图。
[0095]
结合图2和图3所示，该多孔介质孔径分布表征方法，包括：
[0096]
步骤1：获取多孔介质样品的原始孔径和原始孔体积增量；
[0097]
其中，通过高压压汞、氮气吸附、co2吸附或核磁共振对多孔介质样品进行孔径分布测试实验，获得多孔介质样品的原始孔径和原始孔体积增量；所述原始孔体积增量指所述每个原始孔径区间内的孔体积。
[0098]
步骤2：根据原始孔径，确定孔径分布曲线的坐标体系；
[0099]
其中，根据原始孔径，确定孔径分布曲线的坐标体系包括：计算原始孔径的最大值与最小值的商；若最大值与最小值的商大于预设阈值，则坐标体系为对数坐标系，横坐标为孔径的对数，纵坐标为孔体积增量；若最大值与最小值的商小于预设阈值，则坐标体系为普通坐标系，横坐标为孔径，纵坐标为孔体积增量。
[0100]
以取自渤海湾盆地济阳坳陷沙一段的样品为例，样品为灰色泥岩。利用jwbk-200c氮气吸脱附仪器，按照gbt21650.1-2008第2部分对样品进行氮气吸脱附测试，得到测试数据(表1)。表中a列和b列是根据氮气吸附数据，利用bjh模型计算得到的不同大小孔径对应的孔体积增量，c-f列是处理过程及结果数据，也就是说a列为原始孔径，b列为原始孔体积增量。
[0101]
表1普通坐标下氮气吸附数据等间距处理过程
[0102][0103][0104]
具体的，对a列原始孔径数据进行分析，其最小值为2.14nm，最大值为165.67，二者相差近76.4倍，相差不大，因此选取普通横坐标实现该范围孔径分布曲线的制作。
[0105]
步骤3：基于原始孔径和所需的数据点个数，计算每个数据点对应的孔径；
[0106]
其中，基于原始孔径和所需的数据点个数，计算每个数据点对应的孔径包括：基于原始孔径和所需的数据点个数，计算坐标间隔；基于坐标间隔和原始孔径，计算每个数据点对应的孔径。
[0107]
其中，当坐标体系的横坐标为普通坐标系时，采用下述公式计算坐标间隔：
[0108]dint
＝(d
max-d
min
)/(n-1)
[0109]
其中，d
int
为坐标间隔；d
max
为原始孔径的最大值；d
min
为原始孔径的最小值；n为数据点个数；
[0110]
当坐标体系的横坐标为对数坐标系时，采用下述公式计算坐标间隔：
[0111]
logm(d
int
)＝(logm(d
max
)-logm(d
min
))/(n-1)
[0112]
其中logm(d
int
)为坐标间隔对数值；logm(d
max
)为原始孔径的最大值对数；logm(d
max
)为原始孔径的最小值对数，m为基数。
[0113]
其中，当坐标体系的横坐标为普通坐标系时，采用下述公式计算每个数据点对应的孔径：
[0114]di
＝d
min
+d
int
×
(i-1)
[0115]
当坐标体系的横坐标为对数坐标系时，采用下述公式计算每个数据点对应的孔径：
[0116]
logm(di)＝logm(d
min
)+logm(d
int
)
×
(i-1)
[0117]di
＝(logm(di))m[0118]
其中，di为第i个数据点的孔径，d
int
为坐标间隔，d
min
为原始孔径的最小值，m为基数。
[0119]
具体的，a、b列是原始数据，共22个数据点，为了减少数据点个数对结果的影响，并与传统图件进行比对，本实施例确定的目标数据点点数与原始数据点个数一致，即n＝22。
[0120]
a列中最大孔径d
max
＝165.67nm，最小孔径d
min
＝2.14nm，利用公式d
int
＝(d
max-d
min
)/(n-1)，计算目标数据点横坐标间隔为：
[0121]dint
＝(d
max-d
min
)/(n-1)＝(165.67-2.14)/(22-1)＝7.787；
[0122]
以第12个目标点为例说明计算得到目标数据点的孔径，
[0123]d12
＝d
min
+d
int
×
(i-1)＝2.14+7.787
×
(12-1)＝87.80nm。
[0124]
按照同样的方法计算得到其他目标数据点孔径di(如表1中d列的数据)，该数据在普通坐标体系下是以间隔d
int
＝7.787等间距分布的。
[0125]
步骤4：基于原始孔体积增量，计算每个原始孔径对应的累计孔体积；
[0126]
其中，每个原始孔径对应的累计孔体积为小于或等于原始孔径的孔体积增量之和，即
[0127][0128]
其中，v
cn
为第n个原始孔径对应的累计孔体积，vj为第j个原始孔径的孔体积增量，n为小于或等于第n个原始孔径的原始孔径总个数。
[0129]
具体的，根据原始数据计算不同孔径d对应的累积孔隙体积vc，孔径d对应的累积孔体积vc(表1中c列的数据)是小于等于该孔径的孔体积增量v(表1中b列的数据)的求和。
[0130]
如第4个数据点孔径d为3.02，对应的vc为孔径小于等于3.02nm孔隙的体积增量之和：0.00041+0.00058+0.00068+0.00089＝0.00256ml/g。
[0131]
同理，计算得到不同孔径的累积孔体积(表1中c列的数据)。
[0132]
步骤5：基于每个原始孔径对应的累计孔体积，获得每个数据点对应的孔体积增量；
[0133]
其中，基于每个原始孔径对应的累计孔体积，获得每个数据点的孔体积增量包括：对每个原始孔径对应的累计孔体积进行插值，获得每个数据点的累计孔体积；基于每个数
据点的累计孔体积，计算每个数据点的孔体积增量。
[0134]
其中，采用下述公式对每个原始孔径对应的累计孔体积进行插值：
[0135][0136]
其中，v
ci
为第i个数据点的累计孔体积，di为第i个数据点对应的孔径，d
imax
为小于di的原始孔径中的最大值，d
imin
为大于di的原始孔径中的最小值，v
cimax
为d
imax
对应的始孔体积增量，v
cimin
为d
imin
对应的原始孔体积增量；
[0137]
采用下述公式计算每个数据点对应的孔体积增量：
[0138]vi
＝v
ci-v
c(i-1)
[0139]
其中，vi为第i个数据点对应的孔体积增量，v
ci
为第i个数据点对应的累积孔体积，v
ci-1
第i-1个数据点对应的累积孔体积。
[0140]
具体的，计算获得的目标数据点孔径(表1中d列)与原始数据的孔径(表1中a列)不对应，因此需要按照目标数据点孔径di(表1中d列)数据对累积孔体积v(表1中c列)进行插值得到目标点孔径累计孔体积v
ci
(表1中e列)。以第12个目标点为例，说明计算过程：
[0141]
第12个目标数据点孔径d
12
＝87.80nm，在原始孔径(a列)中小于d
12
的孔径最大值d
12max
为72.55，大于d
53
的孔径最小值d
12min
为92.10，d
12max
和d
12min
各自对应的累积孔体积(c列)v
c12max
为0.03229，v
c53min
为0.03606，若选取线性插值模型对d
12
对应的累积孔体积v
c12
进行计算，则
[0142]
同理，确定不同目标数据点孔径di(表1中d列)对应的累积孔体积v
ci
(表1中e列)。
[0143]
则d
12
对应的孔体积增量v
12
＝v
c12-v
c(12-1)
＝0.03523-0.03373＝0.00150ml/g。
[0144]
同理，计算得到不同目标点孔径di(表1中d列)对应的孔体积增量vi(表1中f列)。
[0145]
步骤6：基于每个数据点的孔径和孔体积增量，在坐标体系中绘制孔径分布曲线；
[0146]
以计算得到的等间距分布的孔径di(表1中d列)为横坐标，以计算获得的孔体积增量vi(表1中f列)为纵坐标，选取普通坐标体系，生成孔径分布曲线，如图3所示。
[0147]
图3中绘制了原始数据(表1中a列、b列)的孔径分布曲线和经过本技术处理得到的等间距分布(表1中d列、f列)的孔径分布曲线。两曲线形态差别明显，产生这种现象的原因就是原始数据点分布不均匀，小孔隙数据点间隔小，大孔隙数据点间隔大。比如在原始数据曲线中，因为从19.91nm到26.60nm的间隔突然增大，在26.60nm处出现一个峰值，而在等间距分布曲线中该峰不再存在。原始数据曲线中0-20nm(14个数据点)，峰值较低，曲线幅度低于100-120nm(0个数据点)曲线幅度，在等间距分布曲线中0-20nm(3个数据点)曲线峰值远远高于100-120nm(3个数据点)曲线数值。从实际数据来看，0-20nm孔体积为0.01688ml/g，10-120nm孔体积为0.00309ml/g，表明0-20nm孔体积远高于100-120nm孔体积，与等间距孔径分布曲线表现出的特征更加吻合。
[0148]
步骤7：基于孔径分布曲线的峰值位置，确定主孔及次孔的发育尺寸，从而表征储层的孔隙分布。
[0149]
图4示出了根据本发明的一个实施例的一种多孔介质孔径分布表征方法的基于高压压汞数据的对数坐标孔径分布曲线图。
[0150]
如图4所示，以取自渤海湾盆地济阳坳陷沙三段样品，样品为层状泥岩。利用美国
麦克公司生产的autoporeⅳ9500压汞仪，按照gbt21650.1-2008第1部分对a样品进行测试，得到测试数据(表2)。表中a列和b列是根据压汞数据，利用washburn方程和进汞量得到的不同大小孔径对应的孔体积增量，c-g列是处理过程及结果数据，也就是a列为原始孔径，b列为原始孔体积增量。
[0151]
表2对数坐标下高压压汞数据等间距处理过程
[0152][0153][0154]
具体的，对a列原始数据进行分析，其最小值为3.03nm，最大值为119051.50，二者相差近40000倍，表明该样品孔径分布范围广，既有纳米级孔隙，也有微米级孔隙发育。为了在同一张图上展示不同尺度孔隙的分布特征，横坐标应选取基m大于1的对数坐标，这里将m值确定为10。
[0155]
表2中a、b列是原始数据，共55个数据点，为了减少数据点个数对结果的影响，并与传统图件进行效果比对，本实施例确定的目标点数与原始数据点个数一致，即n＝55。
[0156]
a列中最大孔径d
max
＝1 19051.50nm，最小孔径d
min
＝3.03nm，利用下述公式计算目标点横坐标间隔的对数值为：
[0157]
log
10
(d
int
)＝(log
10
(119051.50)
–
log
10
(3.03))/(55-1)＝0.08509；
100000nm峰面积的3倍，与实际数据更加吻合。
[0174]
实施例一，本技术克服了原始数据分布不均导致的曲线形态不能直观反映孔径分布特征的问题，使得曲线形态在视觉上更能反映孔隙结构特征。
[0175]
实施例二
[0176]
本公开提供一种电子设备包括，该电子设备包括：存储器，存储有可执行指令；处理器，处理器运行存储器中的可执行指令，以实现上述多孔介质孔径分布表征方法。
[0177]
根据本公开实施例的电子设备包括存储器和处理器。
[0178]
该存储器用于存储非暂时性计算机可读指令。具体地，存储器可以包括一个或多个计算机程序产品，该计算机程序产品可以包括各种形式的计算机可读存储介质，例如易失性存储器和/或非易失性存储器。该易失性存储器例如可以包括随机存取存储器(ram)和/或高速缓冲存储器(cache)等。该非易失性存储器例如可以包括只读存储器(rom)、硬盘、闪存等。
[0179]
该处理器可以是中央处理单元(cpu)或者具有数据处理能力和/或指令执行能力的其它形式的处理单元，并且可以控制电子设备中的其它组件以执行期望的功能。在本公开的一个实施例中，该处理器用于运行该存储器中存储的该计算机可读指令。
[0180]
本领域技术人员应能理解，为了解决如何获得良好用户体验效果的技术问题，本实施例中也可以包括诸如通信总线、接口等公知的结构，这些公知的结构也应包含在本公开的保护范围之内。
[0181]
有关本实施例的详细说明可以参考前述各实施例中的相应说明，在此不再赘述。
[0182]
以上已经描述了本发明的各实施例，上述说明是示例性的，并非穷尽性的，并且也不限于所披露的各实施例。在不偏离所说明的各实施例的范围和精神的情况下，对于本技术领域的普通技术人员来说许多修改和变更都是显而易见的。