一种基于多渐消因子自适应动机座旋转调制精对准方法与流程

[0001]
本发明属于惯性导航领域，具体涉及一种基于多渐消因子自适应动机座旋转调制精对准方法，针对动基座精对准耗时长、精度差等特征，实现良好的对准精度。


背景技术：

[0002]
捷联惯导系统是一种自主、信息量全的导航系统，初始对准是捷联惯导系统的关键技术之一。初始对准的精度影响捷联惯导系统的导航精度，初始对准的速度影响载体的快速反应能力。通常初始对准分为粗对准和精对准两个阶段。粗对准利用加速度计、陀螺的输出和已知的重力矢量、地球转速以及当地纬度等参数，直接计算出捷联矩阵。粗对准速度较快，但精度较差。卡尔曼滤波器通常被用于实现捷联惯导系统的精对准，实践证明具有较好的效果。然而受到可观测度的限制，捷联惯导系统初始对准速度和精度相互矛盾，尤其对于基于mems(微机电系统)的捷联惯导系统，其陀螺仪常值漂移及加速度计常值偏置大，限制了其在高端导航需求的应用。如何在最短的时间内取得最好的动机座对准精度成为当前基于mems的捷联惯导系统研究的热点之一。
[0003]
单轴旋转调制是提高mems捷联惯导的对准精度的常用方法。单轴旋转调制只能调节垂直于旋转轴的恒定漂移和偏差，沿旋转轴的常值误差仍然存在，同时对旋转方向的陀螺常值漂移和天向失准角的估计需要很长时间。因此，为了满足高精度导航应用的需要，如何快速估计旋转方向的陀螺常值漂移和天向失准角是需要深入研究的问题。近些年来，一些新的的算法被应用到估计天向失准角和陀螺漂移中，如神经网络法、经纬度辨识法、最小二乘法、扩展辅助量测量等方法。经纬度辨识法能够满足高精度的估计要求，但是估计耗时长，无法满足快速对准的要求；神经网络法估计精度高，但是需要经过大量的数据预学习，且对于不同捷联系统泛化能力差；最小二乘法应用较为广泛，但是其需要的估计时间仍然很长；角速度扩展辅助量测量法是近年发展起来的提高精对准收敛速度的较为实用的方法，但是仅仅限于静基座的精对准，在动机座精对准尚缺乏相关研究。由于载体的实时运动角速度无法精确获取，其限制了角速度扩展辅助量测量法的应用。多渐消因子自适应卡尔曼滤波是解决滤波模型失配的常用方法，渐消因子的获取一般通过经验公式近似估计，影响了滤波效果。随着生物启发式算法的出现，如天牛须寻优算法(bas)，有很强的多变量全局寻优能力及鲁棒性，在一定程度上克服了迭代优化法等方法的耗时长、计算复杂等问题，并在复杂寻优过程中取得了广泛的应用。目前基于bas算法在复杂系统参数实时辨识及控制并在一定程度上取得了较好的效果，但目前在自适应卡尔曼滤波中用于求解渐消因子还没有被提出与应用。
[0004]
提高精对准的实时计算精度也可以在硬件上进行改进，例如采用高性能cpu及gpu的计算机，这种方案在一定程度上可以提高算法的更新迭代速度，却增加了硬件的复杂性，提高了成本，不利于在实践中进行推广应用。


技术实现要素：

[0005]
为解决上述问题，本发明公开了一种基于多渐消因子自适应动机座旋转调制精对准方法，对具有确定参数单轴旋转调制动机座精对准方法进行验证，取得效果能够满足高精度精对准要求。
[0006]
为达到上述目的，本发明的技术方案如下：
[0007]
一种基于多渐消因子自适应动机座旋转调制精对准方法，包括下列步骤：
[0008]
步骤1)，沿z轴的单轴旋转调制矩阵转换模型如下：
[0009][0010]
其中，s系为mems单元坐标系，b为载体坐标系，ω为调制角速度。
[0011]
步骤2)，角速度扩展量测方程推导过程如下：
[0012][0013]
其中,与φ
n
分别为由卡尔曼滤波器估计的转移矩阵及失准角向量，b为载体坐标系，n为导航坐标系。为由载体线速度运动引起的角速度向量，在系泊条件下，为等效的量测噪声向量。为载体的运动角速度向量。为陀螺理论输出。为陀螺实际输出。转换式(2)为：
[0014][0015]
其中，
[0016]
步骤3)，卡尔曼滤波模型为：
[0017][0018]
其中，x为n维状态向量，φ，g，h是关于时间的确定性矩阵函数。w，v为零均值的高斯白噪声。及是由mems及gnss(全球卫星定位系统)计算的载体在导航坐标系n中的线速度。其离散形式为：
[0019][0020]
其中,
是k-1时刻的状态估计值,为一步状态估计值,φ
k/k-1
为一步状态转移矩阵,p
k-1
为预测均方误差阵，g
k-1
为系统噪声分配矩阵,q
k-1
量测噪声分配矩阵,h
k
为量测矩阵,r
k
为量测状态噪声。
[0021]
w
k-1
及v
k-1
分别为系统噪声向量及量测噪声向量。s
k-1
计算方式如下：
[0022][0023]
步骤4)，自适应卡尔曼滤波的策略是选择合适的衰落因子进行调整以抑制发散。通常采用保持残差正交的方法来获得渐消因子，因此，k时刻的新息矢量为：
[0024][0025]
其中，z
k
为量测量。h
k
为量测矩阵，为一次预测状态向量。k时刻新息矢量的协方差阵估计值为：
[0026][0027]
其中，p
k/k-1
为一步预测协方差矩阵，r
k
为量测噪声序列方差阵。c
0,k
计算方法如下：
[0028][0029]
其中，b为渐消因子，其取值范围一般为：0.7～0.95。
[0030]
步骤5)，状态估计的一步预测均方误差阵p
k/k-1
的修正公式为：
[0031][0032]
其中，λ
k
＝diag(s1,s2,
…
s
n
)为对角矩阵，s
i
≥1,i＝1,2,
…
n，n为状态向量的维数；为一步转移矩阵；为系统噪声序列方差阵。新息序列互不相关是线性最优卡尔曼滤波的增益矩阵取k
k
最优值的必要条件，即：
[0033][0034]
上式的等价形式为：
[0035][0036]
多渐消因子自适应卡尔曼滤波的原理即通过选取合适的λ
k
使式(6)近似成立。
[0037]
步骤6)，定义渐消因子搜寻评价函数为：
[0038][0039]
代入式(10)到式(13)得：
[0040][0041]
寻优过程即调节渐消因子矩阵λ
k
使得矩阵ξ(k)所有元素取最小值，则评价函数得等价形式为：
[0042][0043]
其中，n和m分别为矩阵ξ(k)得行数及列数，s
ij
(k)是矩阵ξ(k)的元素，k为迭代次数。寻优过程即使f(x)取得最小值。
[0044]
步骤7)，天牛初始位置为：γ＝[s1,s2,
…
s
n
]
t
＝[1,1,
…
1]
t
,s
i
(i＝1,2,
…
n)是对
角阵λ
k
对应的对角元素。其评价函数值为：f(γ)。定义搜寻方向，通过随机函数设定搜寻方向：
[0045][0046]
其中，τ为搜寻方向，n为状态向量个数，rand为随机向量函数，||
·
||为求模符号。
[0047]
步骤8)，计算甲虫下一步左，右移动方向。搜寻过程开始之前，甲虫不知道食物在哪里，它使用左、右触须来寻找下一个移动方向。如果左触须接收到的食物的气味强度大于右触须，那么下一步就是向左飞，或者向右飞。故左，右触须的位置向量分别是：
[0048][0049]
其中，x
l
为左触须位置，x
r
为右触须位置。d为甲虫触须长度。
[0050]
步骤9)，分别计算左右触须的评价函数值f(γ
l
)及f(γ
r
)。
[0051]
步骤10)，计算天牛下一步位置：
[0052][0053]
其中，δ为移动步距，sgn为符号函数。
[0054]
步骤11)，计算步骤10)的评价函数
[0055]
步骤12)，更新天牛新的下一步全局位置，触须长度及移动步距：
[0056]
更新下一步全局位置：若
[0057]
更新触须长度：d＝0.98d+0.012；
[0058]
更新移动步距：δ＝0.98δ。
[0059]
步骤13)，如果达到最大迭代步数或计算精度满足要求，则结束循环并输出最终渐消因子，输出参数为：λ
k
(i,i)＝γ(i),(i＝1,2,
…
n)。否则返回步骤7)并开始下一个循环。
[0060]
本发明的有益效果是：
[0061]
1.克服了常规动机座精对准方法耗时长，对准精确不高等问题，本文所述控制策略不依赖于复杂的数学计算，可以适用并应用于常规卡尔曼精对准系统中，其对准时间大为缩短，且对准精度有显著提高；
[0062]
2.对单轴旋转系统，常规动机座精对准方法对天向失准角误差及陀螺天向常值漂移的估计耗时长，本方法结合速度扩展量测及多渐消因子自适应卡尔曼滤波法能在较短时间内完成对天向失准角误差及陀螺天向常值漂移的精确估计；
[0063]
3.常规多渐消因子自适应卡尔曼滤波对渐消因子的求取采用近似求解方法，其误差较大，甚至引起系统发散，本方法运用bas寻优法对渐消因子进行迭代求解，具有较高的求解精度及鲁棒性。
附图说明
[0064]
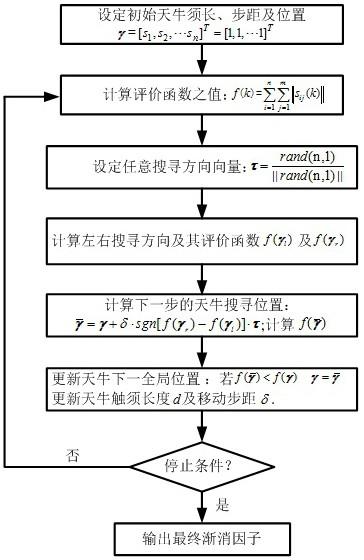
图1是本发明方法的算法设计流程图。
[0065]
图2是本发明方法的单轴旋转调制原理图。
[0066]
图3是本发明方法东向失准角估计值曲线。
[0067]
图4是本发明方法北向失准角估计值曲线。
[0068]
图5是运用本发明方法天向失准角估计值曲线。
[0069]
图6是运用本发明方法天向陀螺常值漂移估计值曲线。
[0070]
图7是运用本发明方法天向加速度计常值偏置估计值曲线。
具体实施方式
[0071]
下面结合附图和具体实施方式，进一步阐明本发明，应理解下述具体实施方式仅用于说明本发明而不用于限制本发明的范围。
[0072]
如图1所示，本发明公开了一种基于多渐消因子自适应动机座旋转调制精对准方法，包括以下步骤：
[0073]
步骤1)，首先推导单轴旋转调制原理，如图2所示。沿z轴的单轴旋转调制矩阵转换模型如下：
[0074][0075]
其中，s系为mems单元坐标系，b为载体坐标系，ω为调制角速度。陀螺及加速度计的常值误差在导航坐标系n系中经过调制后为：
[0076][0077][0078]
其中，为陀螺常值漂移向量,为加速度计常值偏置向量。e,n及u表示东，北，天。为了分析简单，假设其中n为导航坐标系。在一个旋转周期内，ε
n
及
▽
n
的积分为0。
[0079]
步骤2)，角速度扩展量测方程推导过程如下：
[0080][0081]
其中,为陀螺理论输出，为陀螺实际输出，为陀螺输出误差。与φ
n
分别为由卡尔曼滤波器估计的转移矩阵及失准角向量，b为载体坐标系，n为导航坐标系。为由载体线速度运动引起的角速度向量，在系泊条件下，为等效的量测噪声向量。为载体的运动角速度向量。转换式(4)为：
[0082]
[0083]
其中，
[0084]
步骤3)，连续卡尔曼滤波模型为：
[0085][0086]
其中，x为n维状态向量，φ，g，h是关于时间的确定性矩阵函数。w，v为零均值的高斯白噪声。及是由mems及gnss(全球卫星定位系统)计算的载体在导航坐标系n中的线速度。式(6)中变量为：
[0087][0088][0089][0090]
其中，ω
ie
为地球自转角速度，r
m
为子午圈主曲率半径，r
n
为卯酉圈主曲率半径，h为当地地理高度。故卡尔曼滤波其离散形式为：
[0091][0092]
其中,是k-1时刻的状态估计值,为一步状态估计值,φ
k/k-1
为一步状态转移矩阵,p
k-1
为预测均方误差阵，k
k
为增益矩阵，g
k-1
为系统噪声分配矩阵,q
k-1
量测噪声分配矩阵,h
k
为量测矩阵,r
k
为量测状态噪声。w
k-1
及v
k-1
分别为系统噪声向量及量测噪声向量。s
k-1
计算方式如下：
[0093]
步骤4)，自适应卡尔曼滤波的策略是选择合适的衰落因子进行调整以抑制发散。通常采用保持残差正交的方法来获得渐消因子，因此，k时刻的新息矢量为：
[0094][0095]
其中，z
k
为量测量。h
k
为量测矩阵，为一次预测状态向量。k时刻新息矢量的协方差阵估计值为：
[0096][0097]
其中，p
k/k-1
为一步预测协方差矩阵，r
k
为量测噪声序列方差阵。c
0,k
计算方法如下：
[0098][0099]
其中，b为渐消因子，其取值范围一般为：0.7～0.95。
[0100]
步骤5)，状态估计的一步预测均方误差阵p
k/k-1
的修正公式为：
[0101][0102]
其中，λ
k
＝diag(s1,s2,
…
s
n
)为对角矩阵，s
i
≥1,i＝1,2,
…
n，n为状态向量的维数；为一步转移矩阵；为系统噪声序列方差阵。新息序列互不相关是线性最优卡尔曼滤波的增益矩阵取k
k
最优值的必要条件，即：
[0103][0104]
上式的等价形式为：
[0105][0106]
多渐消因子自适应卡尔曼滤波的原理即通过选取合适的λ
k
使式(17)近似成立。
[0107]
步骤6)，定义渐消因子搜寻评价函数为：
[0108][0109]
代入式(15)到式(18)得：
[0110][0111]
寻优过程即调节渐消因子矩阵λ
k
使得矩阵ξ(k)所有元素取最小值，则评价函数得等价形式为：
[0112][0113]
其中，n和m分别为矩阵ξ(k)得行数及列数，s
ij
(k)是矩阵ξ(k)的元素，k为迭代次数。寻优过程即使f(x)取得最小值。
[0114]
步骤7)，天牛初始位置为：γ＝[s1,s2,
…
s
n
]
t
＝[1,1
…
1]
t
,s
i
(i＝1,2,
…
n)是对角阵λ
k
对应的对角元素。其评价函数值为：f(γ)。定义搜寻方向。通过随机函数设定搜寻方向：
[0115][0116]
其中，τ为搜寻方向，n为状态向量个数，rand为随机向量函数，||
·
||为求模符号。
[0117]
步骤8)，计算甲虫下一步左，右移动方向。搜寻过程开始之前，甲虫不知道食物在哪里，它使用左、右触须来寻找下一个移动方向。如果左触须接收到的食物的气味强度大于右触须，那么下一步就是向左飞，或者向右飞。故左，右触须的位置向量分别是：
[0118][0119]
其中，x
l
为左触须位置，x
r
为右触须位置。d为甲虫触须长度。
[0120]
步骤9)，分别计算左右触须的评价函数值f(γ
l
)及f(γ
r
)。
[0121]
步骤10)，计算天牛下一步位置：
[0122][0123]
其中，δ为移动步距，sgn为符号函数。
[0124]
步骤11)，计算步骤10)的评价函数
[0125]
步骤12)，更新天牛新的下一步全局位置，触须长度及移动步距：
[0126]
更新下一步全局位置：若
[0127]
更新触须长度：d＝0.98d+0.012；
[0128]
更新移动步距：δ＝0.98δ。
[0129]
步骤13)，如果达到最大迭代步数或计算精度满足要求，则结束循环并输出最终渐消因子，输出参数为：λ
k
(i,i)＝γ(i),(i＝1,2,
…
n)。否则返回步骤7)并开始下一个循环。
[0130]
本发明中用于仿真验证的参数如下：
[0131]
本系统中单轴旋转调制采用正反整周旋转法，旋转角速度为ω＝20
°
/s。陀螺常值漂移为：0.5
°
/h，随机游走系数为：加速度计常值偏置为：100ug，随机游走系数为：地理位置为：32.12
°
n(纬度),118.24
°
e(经度),23.15m(高度)。载体运动为：θ＝5
°
sin(2πt/6)，γ＝8
°
sin(2πt/7)，ψ＝10
°
sin(2πt/5)。精对准开始前失准角为：φ
e
＝5
′
，φ
n
＝4
′
，φ
u
＝30
′
。采样时间t＝5ms，总仿真时间为1000s。精对准过程结束后，东向及北向失准角误差约为0.5
′
，天向失准角误差约为10
′
，天向陀螺常值漂移估计误差约为0.15
°
/h，天向加速度计常值偏置估计误差约为5ug。其结果可以达到较高的精对准要求。
[0132]
本发明方案所公开的技术手段不仅限于上述实施方式所公开的技术手段，还包括由以上技术特征任意组合所组成的技术方案。